一类非线性Burgers型问题的预测校正紧差分方法

王佳威，张海湘，杨雪花

（湖南工业大学 理学院，湖南 株洲 412007）

1 研究背景

Burgers 方程是描述许多物理现象的模型方程，如流体力学、非线性声学、气体动力学、交通流动力学等。同时，流体动力学中的Naviers-Stokes方程[1-2]忽略压力项后的简单数学模型也可看作Burgers 方程。由于Burgers 方程的重要现实意义，国内外许多学者致力于探讨求解Burgers 方程的数值方法。E.Varöglu 等[3]基于加权残差公式，提出了一种求解Burgers 方程的有限元方法，精确地求解了不同黏度值的Burgers 方程。J.C.López-Marcos[4]研究了一类非线性偏微分方程，并利用Lubich 卷积求积法[5-6]处理积分项，并给出了收敛性等相关理论证明；Chen H.B.等[7]进一步延伸了文献[5-6]的结果，运用Lubich 的二阶卷积求积公式处理积分项，并且用二阶向后差分对时间导数进行离散，空间则采用二阶有限差分格式，对非线性项的处理类似于文献[4]，得到的结果相对于文献[4]有明显的提升。Wang X.P.等[8]对黏性Burgers 方程进行数值求解，得到了一种无条件稳定的紧差分格式；此外，Zhao J.C.[9]提出了以一种具有四阶和六阶精度的紧差分格式求解一类两点边值问题的数值解，并用数值算例证明了差分格式的可行性与有效性。Zhou Y.T.等[10]考虑了非线性分数阶Benjamin-Bona-Mahony Burgers 方程的快速二阶预测-校正方法，并结合均匀网格上空间导数的标准离散化，推导了数值解的离散H1范数误差估计。但上述工作多为对经典Burgers 型方程的研究，而对广义非线性Burgers 型方程的研究工作相对较少。

MacCormack 方法[11-13]是R.W.MacCormack 在1969年提出的一种显式两步预测-校正算法，该方法分为预测步与校正步，两步中对空间一阶导数交替使用向前和向后差分。众多学者将该方法广泛应用于非线性方程的数值解中。E.Ngondiep[14]基于MacCormack 方法和Crank-Nicolson 格式求解混合Stokes-Darcy 模型，得到了一种无条件稳定的预测-校正差分格式。

本文主要讨论下面一类非线性Burgers 方程的预测-校正紧差分格式：

其初始条件和边界条件如下：

其中核β(t)=tα-1，(x,t)∈(0,1)×(0,T]，α∈(0,1)。

2 预备知识

定义1设α∈R+，φ(t)是I=(0，+∝)上逐段连续函数，且在I的子区间上可积，称

为函数φ(t)的α阶Riemann-Liouvile（R-L）分数阶积分[15]。

卷积求积公式[5-6]在离散分数阶积分方面具有明显优势。为了近似Riemann-Liouvile 分数阶积分式（4），下面介绍一阶卷积求积公式。

式中k为时间步长。

求积权重

对区间[0，1]作M等分，区间[0，T]作N等分，记h=1/M，k=T/N，xj=jh，0≤j≤M，tn=nk，0≤n≤N。其中h为空间步长，k为时间步长。

在结点(xj,tn)上考虑u(x,t)，并记ujn=u(xj,tn)，且定义二阶中心差分公式[16-18]为

3 数值离散格式

3.1 预测-校正差分格式

在结点(xj,tn)上考虑定解问题（1）～（3），有

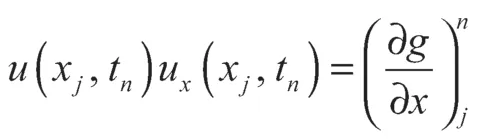
式中r=kα+1。

校正步表达式为

边界条件为

初值条件为

3.2 预测-校正紧差分格式

在建立时间半离散格式（9）的紧差分格式前，首先给出具有四阶精度的一阶导数紧差分公式以及二阶导数紧差分公式。

舍去截断误差o(h4)，整理可得以下二阶导数的紧差分公式：

当j=M-1 时，有

式（11）（12）的截断误差都为o(h4)，且式中系数可由泰勒公式以及待定系数法确定。

记

则可将式（10）～（12）写成如下矩阵形式

式（14）的截断误差为o(h4)，同理，为了求解一阶导数在边界处（j=1，M-1）的值，调整边界处的紧致差分公式。

当j=1 时，有

当j=M-1 时，有

式（15）（16）的截断误差也为o(h4)，且式中系数可由泰勒公式以及待定系数法确定。记

可将式（8）～（10）改写成如下矩阵形式

式（13）（17）即分别为矩阵的一阶导数紧差分公式以及二阶导数紧差分公式。

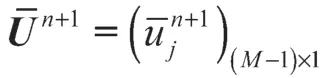
由式（17）可得

由式（13）可得

将式（19）（20）代入式（18），并结合初边值条件，可得到如下Euler 预测-校正紧差分格式

4 数值算例

应用Euler 预测-校正紧差分格式计算下列定解问题

其中精确解为

右端项为

不同步长时数值解和精确解最大误差为

空间收敛阶为

其中b/a为空间步长比；

时间收敛阶为

固定时间步长N=300 000，对α进行不同取值时，差分格式的最大误差以及空间收敛阶与参数M的关系如表1所示。由表1 可以得知，空间收敛阶在4 附近波动。

表1 N=300 000 时x 方向最大误差及空间收敛阶与参数M 的关系Table 1 Maximum error in x direction and the relationship between spatial order and parameter M with N=300 000

固定空间步数M=32，对α进行不同取值时，不同α下差分格式的最大误差以及时间收敛阶与参数N的关系如表2所示。由表2 可以得知，时间收敛阶约为一阶。

表2 M=32 时t 方向最大误差及时间收敛阶与参数N 的关系Table 2 Maximum error in t direction and the relationship between time order and parameter N with M=32

固定α=0.50，则t=0.5 时的数值解与精确解的对比曲线（h=1/10，k=1/8 000）如图1所示；α=0.50，x=0.25 时的数值解与精确解的对比曲线（h=1/8，k=1/64）如图2所示。由图1 和2 可以看出，数值解与精确解较为吻合。

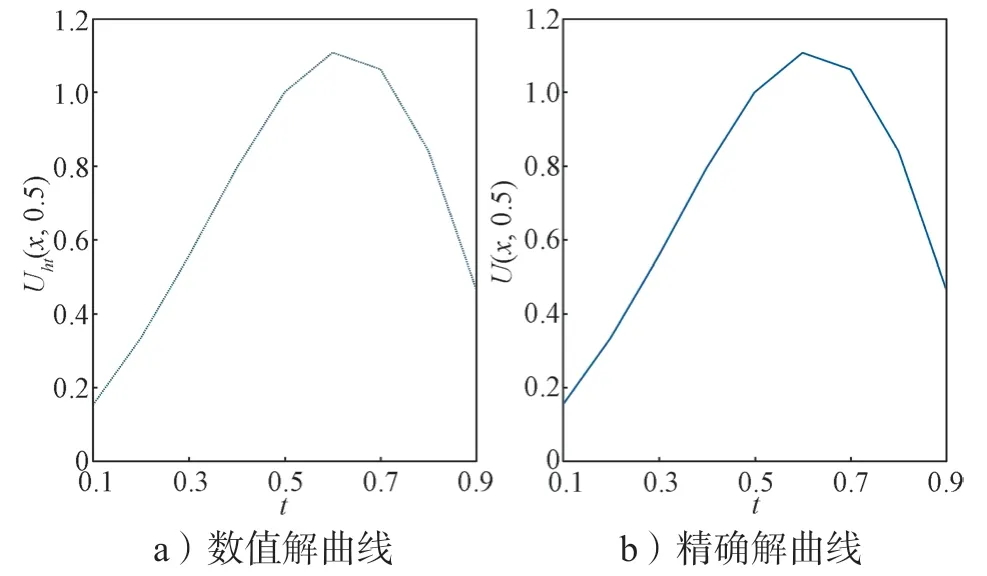
图1 α=0.50,t=0.5 时数值解与精确解曲线Fig.1 Curves of numerical and exact solutions with α=0.50,t=0.5

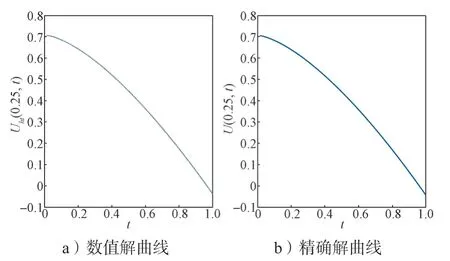
图2 α=0.50,x=0.25 时数值解与精确解曲线Fig.2 Curves of numerical and exact solutions with α=0.50,x=0.25

固定α=0.50，则t=0.50 时不同空间步长的数值解与精确解的绝对误差对比曲线如图3所示，由图可以得知，空间步长越小，其数值解与精确解的绝对误差越小。

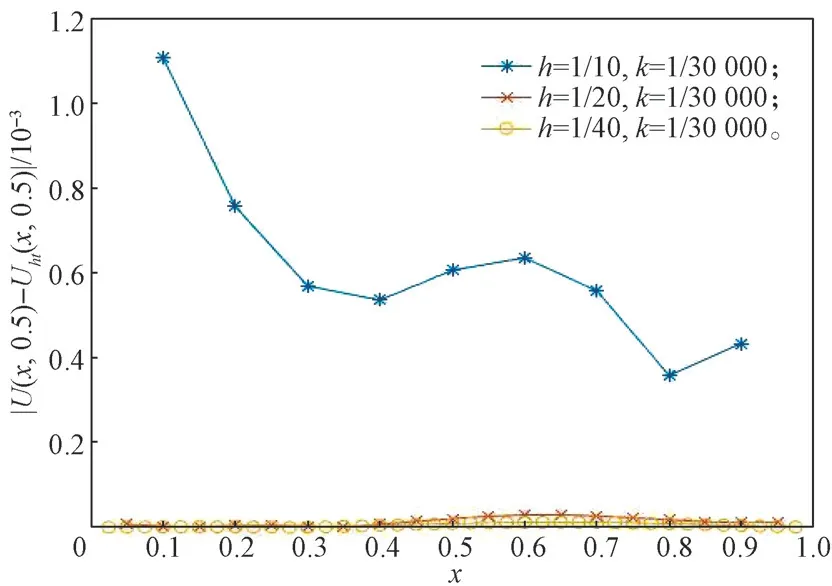
图3 α=0.50,t=0.5 时不同空间步长数值解与精确解的绝对误差曲线Fig.3 Absolute error curves of numerical and exact solutions for different spatial steps with α=0.50,t=0.5

图4 给出了当α=0.50，x=0.25 时，不同时间步长的数值解与精确解的绝对误差对比曲线，由图4 可以看出，时间步长越小，数值解与精确解的绝对误差也越小。

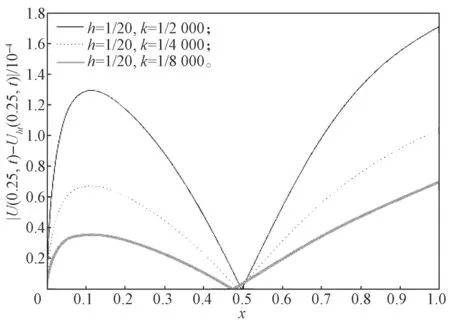
图4 α=0.50,x=0.25 时不同时间步长数值解与精确解的绝对误差曲线Fig.4 Absolute error curves of numerical and exact solutions at different time steps with α=0.50,x=0.25

图5 给出了α=0.50，h=1/20，k=1/4 000 时的数值解与精确解的绝对误差曲面。由图5 可看出，数值解与精确解的绝对误差数量级比较小，说明数值解与精确解比较吻合。

图5 α=0.50 时数值解与精确解的绝对误差曲面(h=1/20,k=1/4 000)Fig.5 Absolute error surface of numerical solution and exact solutions with α=0.50(h=1/20,k=1/4 000)

5 结语

本文研究了一类非线性Burgers 方程的预测-校正紧差分格式，基于矩阵的一阶导数和二阶导数的紧差分公式，以及MacCormack 预测-校正方法，建立了Euler 预测-校正紧差分格式。由数值算例结果可知本文考虑的Euler 预测-校正紧差分格式的收敛阶为o(k+h4)，且最大误差随着剖分数增大而减小。