基于粒子群-遗传混合算法的深沟球轴承优化设计

2024-03-09余江鸿姚齐水唐嘉昌

湖南工业大学学报 2024年1期

叶帅，余江鸿，姚齐水，唐嘉昌，李睿

（湖南工业大学机械工程学院，湖南株洲 412007）

0 引言

随着科技的不断发展，机电产品的性能越来越高，对轴承类关键零部件的性能要求也不断提高。轴承的平稳运行和高寿命是评价轴承服役性能的重要指标，通过对轴承结构参数进行优化设计可以改善轴承的服役性能，其相关研究一直受到科研工作者们的关注[1]。如李敬雍等[2]以轴承的额定动载荷及额定静载荷为优化目标函数，采用粒子群算法（particle swarm optimization，PSO）对轴承进行主参数优化，并通过 AutoCAD 软件的二次开发实现轴承图纸的自动生成与保存。实验结果表明，优化方法能显著提升滚动轴承的数字设计水平。朱晟等[3]利用线性分段函数和指数函数，对学习因子采用异步策略进行调整，实现了粒子群算法中的惯性权重和学习因子随迭代次数的动态调整。考虑到普通粒子群优化算法无法有效求解带约束的优化问题，因此胡启国等[4]基于标准粒子群算法，通过在原目标函数中加入惩罚项，将带约束的优化问题转化为无约束的优化问题，提高了轴承的使用性能。李佳琪等[5]根据轴承的约束条件分析了粒子群算法中的搜索步长、粒子数和迭代次数对轴承优化设计结果的影响。程超等[6]采用遗传算法（genetic algorithm，GA），分别以求得轴承的最大额定动载荷和额定静载荷为目标函数，对轴承进行优化设计，使得轴承的性能有了较大幅度提高。

在各种优化算法中，GA 算法在进行结构参数优化时，虽具有较好的全局搜索能力，但收敛速度较慢，需要进行多次迭代来确定全局最优解。PSO 算法因具有收敛速度快、参数少、算法简单易实现的优点而被广泛应用，但其在进行结构参数优化时，粒子易陷入局部最优解。因此，课题组综合PSO 与GA 的优势，提出了一种粒子群-遗传混合算法，其针对粒子群算法难以求解带约束的优化问题，在目标函数中引入惩罚项，将约束优化问题转化为无约束优化问题；并对易陷入局部最优的粒子位置执行交叉和变异遗传算法操作，将局部最优转化为全局最优。在深沟球轴承优化数学模型的基础上，对轴承结构参数进行优化设计，并将优化结果与PSO、GA 方法的优化结果进行对比分析；最后，进行应力分析和敏感度分析，验证了所提方法的有效性。

1 深沟球轴承优化数学模型建立

1.1 目标函数

在深沟球轴承服役过程中，较高的额定动载荷（Cr）和额定静载荷（Cor）可提高深沟球轴承的平稳运行和承载能力，有利于延长轴承的使用寿命。因此，本文拟以Cr和Cor作为深沟球轴承的优化设计目标函数。

深沟球轴承的额定动载荷可用式（1）进行计算[7]：

式中：bm为常用轴承钢和良好加工方法的额定系数，其取值随着轴承类型而不同，对于深沟球轴承，取值为1.3；Dw为滚珠直径；Z为滚珠数量；fc为与轴承零件几何形状、制造精度及材料有关的系数，其一般表达式为

式中：λ为降低系数，对于深沟球轴承，λ为0.95；γ=Dw/Dj，其中Dj为节圆直径；fi与fo分别为轴承的内、外圈滚道沟曲率半径系数。

在运转过程中，深沟球轴承在载荷作用下会产生一定的塑性变形，若塑性变形量过大，将会在滚道上产生不可逆的损伤，导致轴承的使用寿命下降。而当轴承在静止条件下，所受的载荷不超过额定静载荷时，则可有效地避免塑性变形对轴承正常运转的影响。因此，提高轴承的额定静载荷，对提高轴承的实际寿命以及运行的平稳性有着重要意义，深沟球轴承的基本额定静载荷计算方法[8]如式（3）所示：

式中：ai、bi分别为滚珠与轴承内圈滚道接触椭圆量纲为1 的长半轴与短半轴，其具体数值可以查询表1获得[4]。

表1 部分量纲为1 的接触参数Table 1 Partial contact parameters with dimension 1

为提高分析效率，以Cr与Cor的加权之和G作为优化目标函数，并命名为联合额定载荷，以便判断Cr与Cor在优化目标中的重要程度，定义如式（4）：式中：a1、a2为线性加权系数，且a1+a2=1。

综合上述，所构造的目标优化模型，要使得深沟球轴承的性能最佳，就需要G的值越大。通常优化求解时，只能求解函数的极小值问题。因此，通过对表达式G加负号来建立优化目标模型Y，将极大值问题转换成极小值问题来求解，表达式如下：

1.2 设计变量

根据式（1）～（5），将滚动体直径Dw、节圆直径Dj、滚动体数目Z、外圈滚道沟曲率半径系数fo和内圈滚道沟曲率半径系数fi共5 个参数作为深沟球轴承的优化设计变量，如式（6）所示：

1.3 约束条件

1）滚动体直径约束。滚动体直径影响着深沟球轴承的Cr，根据滚动轴承设计经验，轴承滚动体直径应满足：

式中：KDmax、KDmin为轴承直径系列和滚动体强度有关的经验常数，对于深沟球轴承，KDmax为0.8，KDmin为0.5；D为轴承的外径；d为轴承的内径。

2）节圆直径约束。节圆直径决定了轴承内外圈的厚度，对轴承疲劳寿命有一定的影响，为了保障深沟球轴承的实际使用寿命，轴承的节圆直径应满足：

式中：e为轴承正常旋转的常量[9]，对于深沟球轴承，e取0.1。

3）滚动体数量约束。如图1所示，为了便于深沟球轴承装配，在轴承的优化设计中，滚动体的数量应满足以下条件[9]：

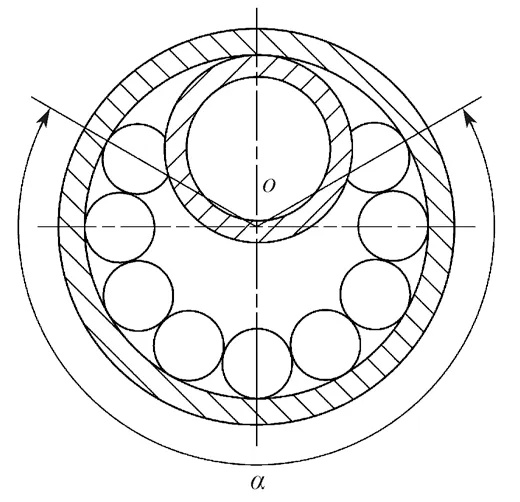
图1 深沟球轴承滚动体装配示意图Fig.1 Assembly diagram of rolling elements of deep groove ball bearing

式中：αmax为滚动轴承的最大装配角，对于深沟球轴承，αmax取4.712 4 rad。

4）壁厚约束。深沟球轴承主要承受径向载荷，滚动体与内圈滚道之间的应力大于外圈滚道所承受的应力，故壁厚应满足如下条件：

式中：ε为与轴承外圈强度有关的常量，对于深沟球轴承，ε取0.1。

5）沟曲率半径系数约束。轴承沟曲率半径系数是影响轴承动态性能的重要结构参数，在轴承的设计与优化中，内、外圈滚道的沟曲率半径系数应满足如下条件[10]：

2 优化算法与计算流程

2.1 粒子群优化算法

PSO 是J.Kennedy 和R.Eberhart 共同提出的一种新群体智能优化算法[10]，用于解决多种方案中的智能寻优问题，在机械结构优化设计领域中得到了广泛的应用。该方法利用初始生成的N个随机粒子，经过反复迭代，使得粒子在多维中找到最优解。PSO通过追随自身寻找到的最优解（个体极值pbest）和整个粒子群寻找到的最优解（全局极值gbest）来更新自己的位置，粒子个体与群体之间的速度和位置更新公式如下：

在粒子群算法中，惯性权重w是随着进化代数的增加而线性递减的减函数，如式（13）所示：

式中：gen为粒子群当前迭代次数；genmax为粒子群最大迭代次数。

2.2 罚函数

罚函数法是一种间接算法，其核心思想是利用原问题的约束函数和目标函数构造一个新的目标函数，即新的目标函数包括原函数和所有约束函数，并加入一个可变的惩罚因子[11]。当惩罚因子不断变化时，会得到一系列函数，对不满足约束条件并试图越过约束边界的不可行点进行惩罚，更新每个新目标函数的极值，直至收敛到原问题的最优解。对于一个非线性约束优化问题，一般可表示为

使得：

式（14）（15）中：f(x)为目标函数；gi(x)为不等式约束；hi(x)为等式约束。

因此，惩罚函数可以通过把式（14）的问题进行如下转化：

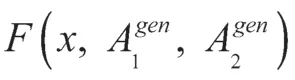
2.3 交叉、变异操作

交叉与变异操作是GA 的重要内容，交叉操作将父代个体配对，进行一个或者多个基因位置重组，增加最优个体的出现机率，提高了全局搜索能力；变异操作通过改变个体内部的基因，来克服个体早熟收敛[12]。因此，在PSO 中引入GA 的交叉、变异操作，可以使得粒子更加适应种群环境，从而找到问题的全局最优解。

在粒子群-遗传混合算法中，当每次迭代出现的全局最优值与上一代的全局最优值相同、出现的个数之和超过图2 所设置的kmax时，则默认此时粒子已经陷入局部最优。此时，将对下一代粒子的位置进行GA 的交叉与变异操作，产生子代，然后与父代进行比较，选取适应度值较高的子代再进行下一代进化。通过引入GA 的交叉、变异操作，可以增加粒子的多样性，从而跳出局部最优。

图2 粒子群-遗传混合算法流程Fig.2 Particle swarm optimization genetic hybrid algorithm process

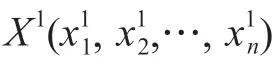
式中β由式（19）动态随机决定。

式中：rand为常数，且在0～1 之间随机变动；mu为交叉算子的分布指数，且mu＞0，一般取mu=1。

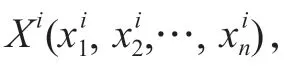
式中：t为子代个体中染色体的位置；η由式（21）动态随机决定。

式中：mum为变异算子的分布指数，且mum＞ 0，一般取mum=1。

2.4 粒子群-遗传混合算法的优化操作

根据粒子群-遗传混合算法的运行原理，利用罚函数处理深沟球轴承优化设计中的约束条件，以确保目标函数值在合理范围内。当粒子陷入局部最优时，结合GA 的优势，对粒子个体进行交叉、变异操作，扩大寻优区域，从而求得全局最优解，具体优化流程如图2所示，具体的优化操作步骤如下：

步骤1初始化相关参数。

步骤2初始化种群各个粒子的速度与位置，随机生成粒子群。

步骤3根据罚函数来惩罚，计算粒子的适应度值，确定粒子的全局最优值和局部最优值。

步骤4根据式（14）更新粒子的惯性权重，更新当前粒子的速度和位置。

步骤5判断迭代出现的全局最优值与上一代的全局最优值同时出现的个数是否超过所设的kmax，若超过，则对粒子群中的每个粒子位置进行GA 的交叉和变异操作；反之则进行下一步。

步骤6再次利用罚函数更新粒子的目标适应度值，同时更新粒子的全局最优值与局部最优值。

步骤7判断迭代出现的全局最优值与上一代的全局最优值是否相同，若相同，则在k值的基础上加1；若不相同，则k值归零。

步骤8该粒子群运行到所设的最大迭代次数genmax时，即得到全局最优解。

3 算例分析

3.1 6206 型深沟球轴承算例分析

本研究以在新能源汽车电驱系统中广泛应用的6206 型深沟球轴承为优化对象。优化前轴承外径为62 mm、内径为30 mm，曲率和为0.591 6，约束系数ai=3.738，bi=0.416 6，f1=1.5。根据所提粒子群-遗传混合算法，设定种群规模N=50，最小惯性权重wmin=0.4，最大惯性权重wmax=0.9，个体学习因子和社会学习因子为c1=c2=1.5，最大迭代次数genmax=500，惩罚因子A1=1×1012，A2=0，最大粒子速度vmax=1，最小粒子速度vmin=-1，交叉概率pcross=0.7，变异概率pmutation=0.1，交叉算子的分布参数mu=10，变异算子的分布参数mum=30，允许全局最优值重复出现的最大个数kmax=4。通过设置线性加权系数a1、a2，在不同的优化目标下对深沟球轴承进行优化设计。

同时，为了验证粒子群-遗传混合算法在优化设计上所达到的效果，在相同的优化参数条件下，分别采用粒子群算法和遗传算法对6206 型深沟球轴承进行优化，对比其优化结果。

当线性加权系数a1=1、a2=0 时，优化目标对象为Cr，优化后的结果如图3所示。

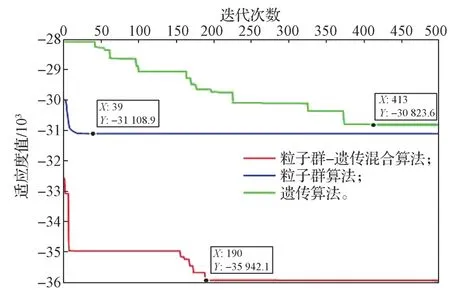
图3 6206 型深沟球轴承Cr 优化结果Fig.3 Cr optimization results of 6206 deep groove ball bearing

由图3 可以得知，轴承的Cr在粒子群-遗传混合算法下，经过190 次迭代后收敛于35 942.1 kN，达稳定值；在粒子群算法下，经39 次迭代后收敛于31 108.9 kN，粒子已陷入局部最优解；在遗传算法下，经413 次迭代后收敛于30 823.6 kN，还有寻找最优解的可能。各算法对应的轴承设计变量值见表2。

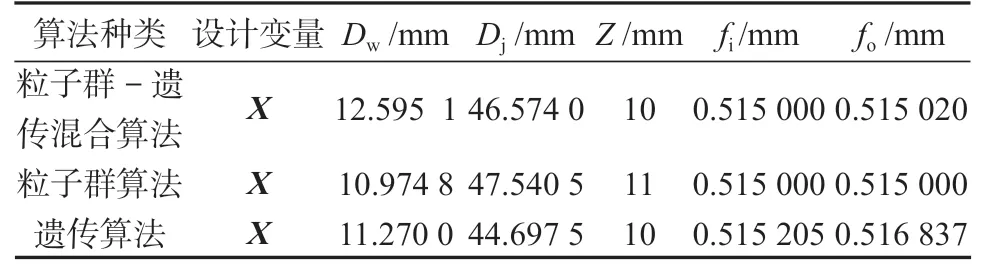
表2 6206 型深沟球轴承Cr 优化后的设计变量值Table 2 Design variable values of 6206 deep groove ball bearing after Cr optimization

当线性加权系数a1=0、a2=1 时，优化目标对象为Cor，优化后的结果如图4所示。

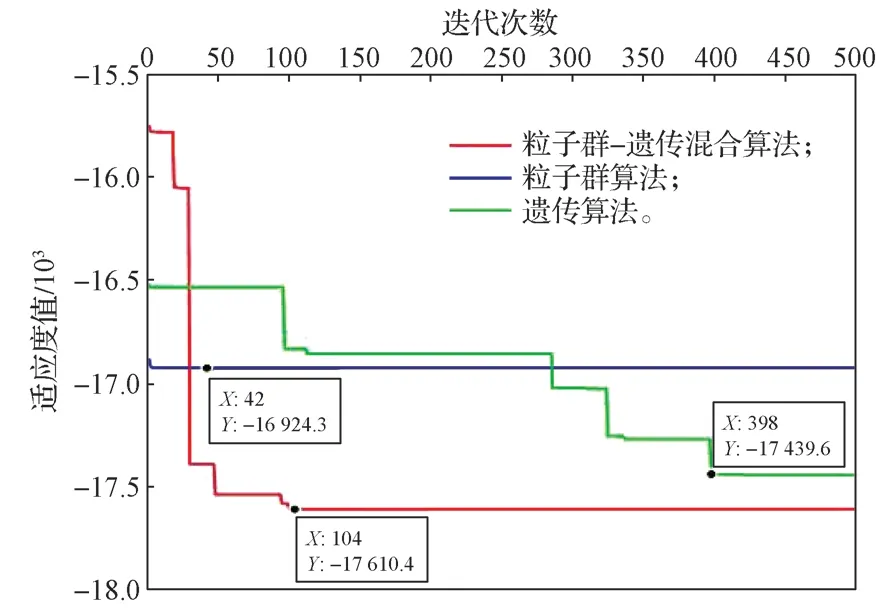
图4 6206 型深沟球轴承Cor 优化结果Fig.4 Cor optimization results of 6206 deep groove ball bearing

由图4 可知，轴承的Cor在粒子群-遗传混合算法下，经过104 次迭代后，收敛于17 610.4 kN，达到稳定值；在粒子群算法下，经过42 次迭代后，收敛于16 924.3 kN，粒子已陷入局部最优解；在遗传算法下，经过398 次迭代后，收敛于17 439.6 kN，且还有寻找最优解的可能性。轴承在各算法下对应的设计变量参数如表3所示。

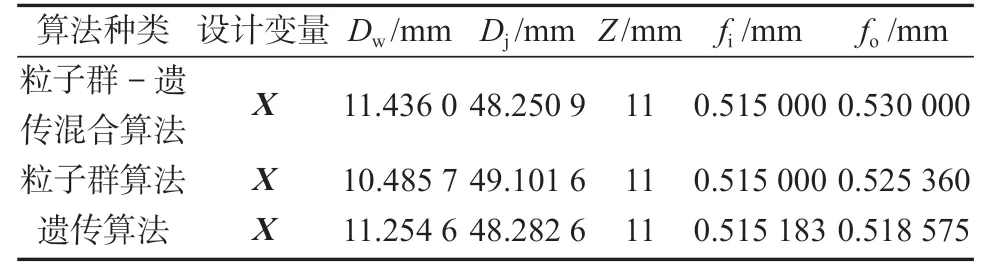
表3 6206 型深沟球轴承Cor 优化后设计变量值Table 3 Design variable values of 6206 deep groove ball bearing after Cor optimization

当线性加权系数a1=0.5、a2=0.5 时，优化目标对象为联合额定载荷，优化后的结果如图5所示。

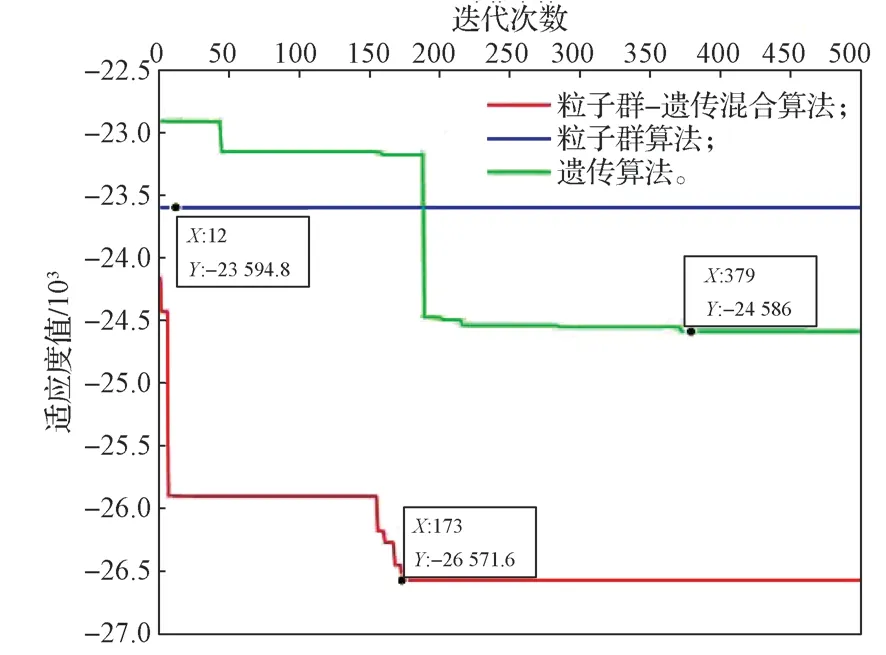
图5 6206 型深沟球轴承联合额定载荷优化结果Fig.5 Optimization results of combined rated load of 6206 deep groove ball bearing

由图5 可看出，轴承的联合额定载荷在粒子群-遗传混合算法下，经173 次迭代后，收敛于26 571.6 kN，达到稳定值；在粒子群算法下，经12 次迭代后，收敛于23 594.8 kN，粒子已陷入局部最优解；在遗传算法下，经过379 次迭代后，收敛于24 586 kN，还有寻找最优解的可能性。在各对应的算法下，轴承设计变量参数如表4所示。

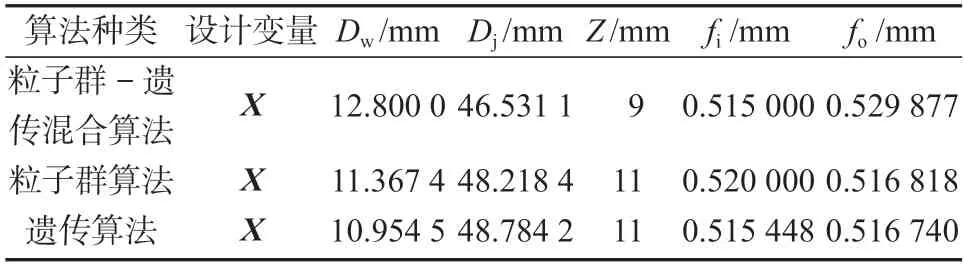
表4 6206 型深沟球轴承联合额定载荷优化后设计变量值Table 4 Design variable values of 6206 deep groove ball bearing after optimization of the combined rated load

3.2 6206 型深沟球轴承有限元分析

为了验证所提粒子群-遗传混合算法应用于轴承结构参数优化的有效性，基于优化得到的6206 型深沟球轴承，联合额定载荷设计变量参数，施加16 kN 的径向载荷，建立有限元模型并进行仿真分析，得到优化前后的接触应力云图如图6所示。优化前的最大接触应力为1 315 MPa，优化后的最大接触应力为898.2 MPa。相比于优化前，深沟球轴承所承受接触应力下降了31.7%，这有益于提升轴承实际使用性能和疲劳寿命。

3.3 敏感度分析

基于优化后的结构参数分析制造误差对轴承性能影响的敏感程度，可以为提高轴承服役水平提供更加全面的参考。在深沟球轴承的实际制造过程中，±0.5%的制造误差是其最常见的误差范围[13]。因此，为确定优化后的深沟球轴承性能，本文以优化后的6206 型深沟球轴承联合额定载荷设计变量为例，分析当设计变量参数Dw、Dj、fi、fo的制造误差分别为-0.5%和+0.5%时，目标函数Cr和Cor的变化情况。当制造误差为-0.5%和+0.5%时，目标函数Cr和Cor的敏感度分析结果如表5 和表6所示。

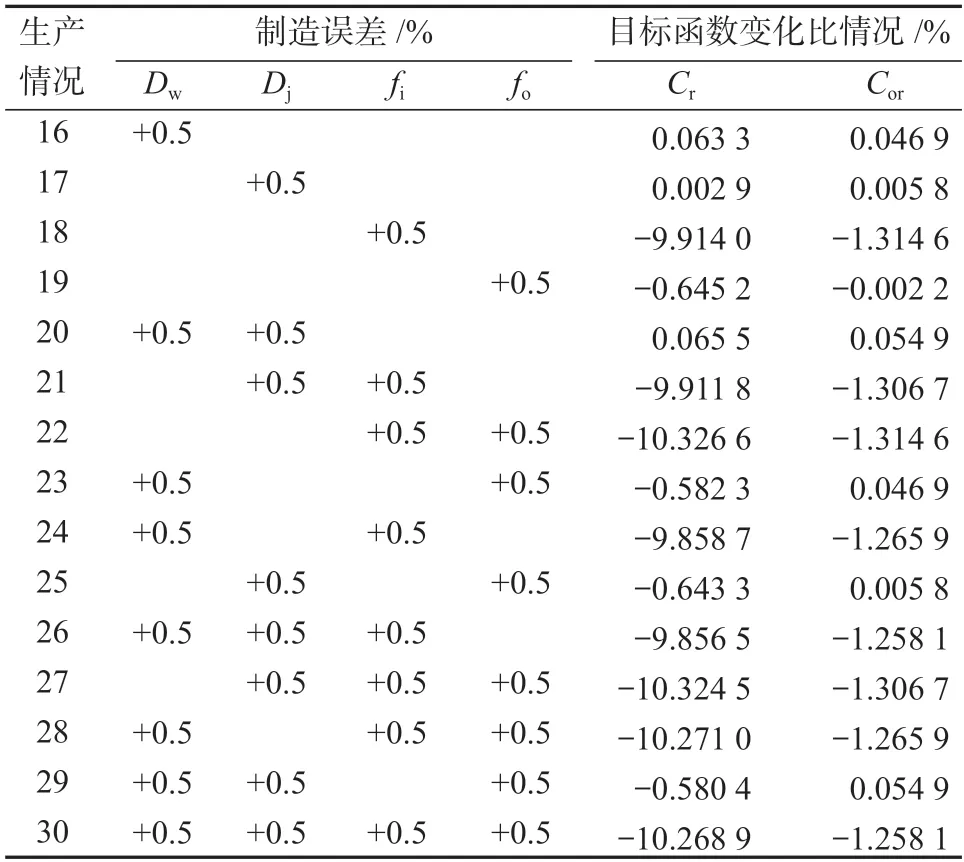
表6 制造误差为+0.5%的敏感度分析结果Table 6 Sensitivity analysis results with a manufacturing error of +0.5%

表5 和6 中的生产情况3、6、7、9、11～13、15、19、22、23、25、27～30 的状态不满足深沟球轴承的约束条件。因此，上述生产情况将不进行后续的分析。

由表5 可知，当制造误差为-0.5%时，生产情况为4、8、10 和14 时，轴承性能较好，为1、2 和5 时，轴承性能较差；当Dw变化为-0.5%时，Cr和Cor分别变化为-0.061 9% 和-0.051 3%；当Dj变化为-0.5%时，Cr和Cor分别变化为-0.001 4%和-0.010 2%；当fo变化为-0.5%时，Cr和Cor分别变化为0.639 4%和-0.002 2%。

由表6 可知，当制造误差为+0.5%时，生产情况16、17 和20 时的深沟球轴承性能较好，为18、21、24 和26 时轴承性能较差；当Dw变化为+0.5%时，Cr和Cor分别变化为0.063 3%和0.046 9%；当Dj变化为+0.5%时，Cr和Cor分别变化为0.002 9%和0.005 8%；当fi变化为+0.5%时，Cr和Cor分别变化为-9.914 0%和-1.314 6%。

从上述关于表5～6 的分析中可以得出，当制造误差为-0.5%时，目标函数Cr和Cor在整体上是优于最终的优化值，但容易受深沟球轴承几何约束条件的限制，符合条件的不多；当制造误差为+0.5%时，目标函数Cr和Cor在整体上劣于最终的优化值。因此，在制造生产中，要避免制造误差为正；制造误差为负时，要根据深沟球轴承的几何约束条件进行校验。