基于长期气温模拟的混凝土坝结构健康监测

2024-03-08饶滨

地下水 2024年1期

饶滨

(思南县水务局,贵州思南 565100)

0 引言

水坝兼具供水、防洪、灌溉、航运、泥沙控制和水力发电等综合功能,大坝的安全影响着大坝周围地区的人身财产安全和生态环境。大坝的结构响应受到许多因素的影响,包括静水压力、蠕变引起的温度和时间效应、碱骨料反应等[1]。目前,已经开发了许多统计和混合数学模型来描述和预测大坝的结构行为。基于有限元法的数值模型可以准确地分析温度和水位变化的耦合效应,在分析特殊或非常规条件时提供了较大的灵活性[2]。同时,基于多元线性回归的统计模型在大坝行为建模中已被证实了可行性,所采用的回归模型包括线性回归模型、逐步回归模型、基于主成分分析的回归模型、独立成分回归和偏最小二乘回归等[3]。随着人工智能的发展,机器学习技术被应用于建立基于数据的大坝结构健康监测预测模型,基于机器学习算法的数据驱动模型可以提供比统计模型更准确的大坝行为预测,更适合建模非线性效应以及输入变量和大坝响应之间的复杂相互作用[4]。径向基函数网络是一种具有非正弦隐层单元的前馈神经网络,通过将神经网络的设计视为高维空间中的曲线拟合问题,具有结构简单、训练速度快、控制参数少等特点[5]。径向基函数网络除了理论分析外,如渗流预测、边坡稳定性评估和热分析等工程问题均具有可行性。

本文提出了一种基于长期气温的径向基函数网络大坝健康监测模型,考虑不同年份温度变化对大坝响应的影响,并在实际案例中测试了径向基函数网络模型的性能,量化了不同模型的训练数据和测试数据的预测误差,为大坝以及其他大型结构的健康监测建模提供参考。

1 大坝运行预测

从静态健康监测系统获得的数据通常基于环境因素和大坝响应之间相关性的统计模型进行分析。环境因素包括水库水位、大坝内部温度、气温和水库外部温度、地震等。大坝响应指位移、扬压力、渗流、裂缝、应力和应变等。将大坝的实际响应与数学模型的预测值进行比较,以检测模型的预测误差。大坝位移是大坝健康运行的重要指标。因此,本文对位移监测建模问题进行了研究。

1.1 静水-季节-时间模型

大坝的响应可分为两部分:静水荷载和温度引起的可逆效应、蠕变和碱聚集反应以及其他损伤引起的不可逆效应。静水-季节-时间模型是混凝土坝安全控制最常见的统计模型。响应的一般统计模型可用公式(1)表示:

ΔD=Δh+ΔT+Δt+ε

(1)

式中:ΔD为观测到的水平位移,mm;Δh为静水载荷引起的响应,mm;ΔT为温度变化引起的响应,mm;Δt为不可逆的时间效应,mm;ε为常数,单位为mm。

1.1.1 静水效应

静水压力的影响通常表示为基于力学分析的多项式函数,见公式(2)。

Δh=a0+a1h1+a2h2+a3h3

(2)

式中:Δh为静水载荷引起的响应,mm;a1、a2和a3为系数。对于混凝土重力坝,可以使用h的三次多项式函数。对于拱坝,通常使用四次多项式函数。

1.1.2 温度效应

温度效应是由于大坝混凝土和基础的温度变化引起的。在大坝和地基中安装测温装置时,温度变化引起的位移可以表示为记录的内部温度数据的函数。对于运行多年的混凝土大坝,内部温度可视为准稳态。大坝对季节性温度的响应认为遵循周期性演变。温度变化的影响可以计算为谐波正弦函数的组合,见公式(3)。

ΔT=b0+b1sin(s)+b2cos(s)+b3sin(2s)+b4cos(2s)

(3)

式中:ΔT为温度变化引起的响应,mm;b1、b2、b3和b4为系数,s=2πr/365,r是从年初(1月1日)到观测日的天数,即从监测开始日到响应观测日的天数。

1.1.3 时间效应

大坝的不可逆变形主要与蠕变有关,蠕变随时间呈渐近变化。时间效应变形通常在初始蓄水期间迅速发展,并随着时间的推移趋于稳定。因此,通常使用等式(4)来表示。

Δt=c0+c1θ+c2ln(θ+1)

(4)

式中:Δt是不可逆的时间效应,mm。θ=t/100,t是天数,c0、c1、c2为系数。

对于运行多年的大坝,采用时间的线性函数。根据多元线性回归理论,式(2)～(4)的系数由最小二乘法估算。

1.2 基于气温的大坝健康监测模型

大坝的温度变化主要受外界温度变化的影响。因此,外部温度变化可以反映大坝温度的变化,但内部温度和外部温度变化之间存在一定滞后效应。因此,当连续记录气温数据时,可使用测量的分段气温数据来模拟温度效应。

2 基于长期气温的径向基函数网络模型

2.1 径向基神经网络

径向基神经网络是一种具有非正弦隐层单元的前馈神经网络,通常由输入层、隐层和输出层组成。径向函数是一类特殊的函数,典型特征是响应随着距中心点的距离单调地减小或增大。径向基网络比标准前馈-反向传播网络需要更多的神经元,但通常设计时间显著少于训练标准前馈所需时间。径向基神经网络也被称为局部感受野网络,只有当输入落在输入空间的小局部区域内时,隐藏层中的基函数才会对输入刺激产生显著的非零响应。

径向基神经网络只有隐藏层和输出层之间的连接权重,可以通过线性最小二乘法获得。径向基神经网络的学习通过求解线性方程来确定权重。考虑到研究中的输入向量在时间上均匀分布,采用了精确的径向基神经网络,这意味着所有输入向量都被选为中心。使用简单的试错方法对径向基神经网络模型的不同分布值进行了检验,通过求解线性伪逆解来计算最小化输出误差。

2.2 基于长期气温的变量集

基于气温数据的大坝健康监测模型建立后,模型的性能需要进一步验证。根据初步测试,使用气温的现有模型没有使用谐波正弦函数的模型表现性能优异,不能反映不同年份温度变化对大坝响应的影响。如图1所示,相邻两年的最高和最低气温可能相差5℃～10℃。使用长期气温数据进行更合理的模拟,采用更多年份的气温数据的变量集来模拟温度效应。

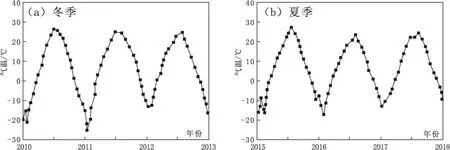
图1 不同年份的温度变化

除了气温外,太阳辐射和水温也对热效应有很大影响。同时,太阳辐射也影响气温,而气温进而影响水温。因此,空气温度作为温度效应模拟的主要代表因素,虽然输入变量中没有明确考虑太阳辐射和水温,但机器学习技术可以在一定程度上从气温数据中挖掘其之间的影响。

2.3 基于长期气温的大坝健康监测模型

多元线性回归方法不能准确地近似高度非线性的关系。采用更灵活的径向基函数网络模型,具有适于对大坝行为预测问题的非线性进行建模的形式。对于大坝健康监测建模问题,在不同的情况下需要不同的输入变量。对于位移建模,当采用谐波正弦函数进行温度效应模拟时,输入可以是矢量,模型的输出是大坝位移。为了建立上述径向基函数网络模型,需要基于已知数据集的训练过程。在建模之前对数据进行归一化,以改善不良的输入变量缩放对径向基函数网络模型建模的影响。模拟精度通过平均绝对误差、均方根误差、最大绝对误差和相关系数等指标进行评估。基于气温的大坝健康监测径向基函数网络模型流程图如图2所示。

图2 基于气温的大坝健康监测径向基函数网络模型流程图

3 工程实例

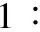
3.1 建立数据集

建立健康监测系统评估混凝土大坝的运行状况,该系统由多个仪器组成,可以监测和测量水库水位、气温、水平和垂直位移、渗流等数据,建立真空激光准直系统来测量位移。同时,每天测量蓄水位和日平均气温数据。位移每月测量1～3次。数据集建立于2008-2020年,采用2008-2018年选取的样本的数据集作为训练集,采用2018-2020年选取的样本数据集作为测试集。对于径向基函数网络模型,必须在模拟之前预先定义参数分布。

3.2 基于谐波正弦函数的模型性能

基于谐波正弦函数的多元线性回归模型的预测结果与坝顶水平位移实测值的比较如图3所示。基于谐波正弦函数的径向基函数网络模型的性能如图4所示。可以观察到,对于基于谐波正弦函数的模型,径向基函数网络模型在训练数据上的表现优于多元线性回归。对于测试数据,预测误差的改善并不明显。

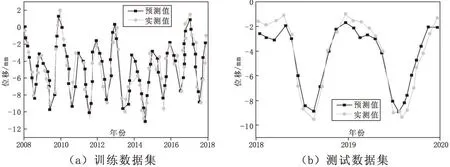
图3 使用谐波正弦函数的多元线性回归模型性能

图4 使用谐波正弦函数的径向基函数网络模型性能

3.3 基于气温的径向基函数网络模型性能

本文采用了长时间的气温数据建立基于长期气温的径向基函数网络模型,在变量集上测试了多元线性回归模型。结果证明,使用两年气温的多元线性回归模型表现最好,但精度不如基于谐波正弦函数的多元线性回归模型。

在基于气温的变量集上测试径向基函数网络模型,随着采用的气温数据的增加,误差显著减少,与基于气温的多元线性回归模型相同。然而,当采用气温变量集来模拟大坝运行时,径向基函数网络模型的预测结果远优于多元线性回归模型。基于长期气温的径向基函数网络模型的性能如图5所示。可以看出,静水-季节-时间模型在径向基函数网络情况下比多元线性回归拟合得更好,残差也大大减少。较大的值将导致训练误差的增加,较小的值将造成测试误差的增加,很难选择适用于所有变量集的相同分布值[6]。对于每个变量集,应研究分布对预测精度的影响,以选择最合适的变量集。

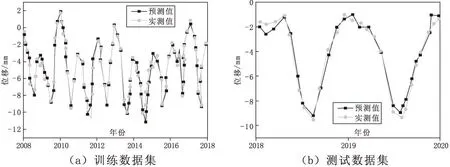
图5 基于长期气温的径向基函数网络模型的性能

3.4 不同模型的直接比较研究

综合分析基于气温数据的径向基函数网络模型结果,并与传统的基于调和函数的多元线性回归模型的结果进行对比,可以观察到,无论是训练数据集还是测试数据集,径向基函数网络模型的预测误差都比多元线性回归模型小得多。与多元线性回归模型的结果相比,径向基函数网络模型在训练和测试场景中的最大绝对误差分别降低了39.66%和31.07%,均方根误差分别降低了26.84%和33.18%。