单位涌水量的换算方法对比与讨论
2024-03-08周立涛
周立涛,李 旭
(安徽理工大学 地球与环境学院,安徽 淮南 232001)
0 前言
矿区的含水层富水性的等级评价可按单位涌水量来进行判定,依据《矿区水文地质工程地质勘探规范》[1]、《煤炭矿井防治水设计规范》[2]中规定标准的钻孔单位涌水量是以孔径91 mm、抽水水位降深10 m为准。但是在满足“一孔多用”及研究区特定水文地质条件下,多数钻孔的孔径并非91 mm、降深也很难精确到10 m,致使单位涌水量很难进行对比分析,更难以评价矿区的含水层富水性。因此,需要对单位涌水量进行标准化的换算。
奚砚涛等人指出根据抽水试验规程对抽水试验数据进行单位涌水量换算具有必要性、科学性和实践性[3]。薛建坤等人对岱庄矿区单位涌水量进行误差统计得出如果降深值太小或太大,会导致计算的 q 值偏差很多,从而导致人们对含水层富水性产生错误的认识[4]。陈阳基于VB6.0软件对单位涌水量计算方法进行探讨得出采用VB6.0软件可以有效数据的处理效率和参数的准确性[5]。孙尚云等[6]和庄保辉等[7]提出采用 Excel函数和图表功能处理换算过程中的 Q-S 曲线拟合问题,快速、合理地解决了曲线类型判断及单位涌水量 q 的计算。刘埔等人提出Q-S曲线的MATLAB拟合单位涌水量换算方法,通过比较拟合结果的多个误差评价参数,较好的解决了曲线 拟合的精确度问题,使得Q-S曲线拟合效果易于分析对比,回归方程的确定更加准确[8]。
目前,针对单位涌水量换算问题,总体思路是对降深进行修正和井径换算,可以采用VB6.0、MATLAB和Excel软件进行辅助换算。然而,在实际操作计算中,为简化计算通常将R孔和R91进行等效处理,即R91的数值用R孔的数值代替。实际上R孔和R91是存在差异的,若等效处理,这必然会影响含水层富水性评价的精度。为此,本研究基于前人研究的3次抽水试验实测数据,首先采用迭代方法进行井径的换算,并分别计算R91和R孔,之后采用MATLAB软件进行Q-S曲线的拟合得出单位涌水量并进行含水层富水性评价。此方法避免了修正好的降深发生改变的问题,并且提高了计算精度。此外,将计算的结果与传统的方法进行对比,分析影响半径变化对计算结果误差的影响。
1 单位涌水量的换算方法
1.1 传统的计算方法
1.1.1 降深修正
根据抽水试验获得Q和S的三组数据,利用最小二乘法或图解法确定Q-S曲线的类型,有直线型、抛物线型、幂函数型或对数型。目前可以借助VB6.0、Excel和MATLAB软件进行Q-S曲线的拟合,得到Q-S的数学关系式。将S=10 m带入到获得的Q-S曲线,计算得到实际孔径时降深为10 m时的涌水量。
1.1.2 井径修正
降深修正后,由于井径的差异,因此要进一步对井径进行修正。地下水向承压水井的稳定运动理论满足承压含水层完整井稳定流时Dupuit公式[10],如式(1):
(1)
式中:S井中水位降深,m;Q为抽水井流量,m3/d;M为含水层厚度,m;K为渗透系数,m/d;r为井的半径,m;R为影响半径,m。
针对同一含水层不同流量抽水时的K值,在计算公式一致的情况下,理论上差别不大。一般情况下采用集哈尔特经验方程[11],如下式(2):
(2)
根据抽水试验已知水位降深、抽水井流量、含水层厚度和井的半径,采用迭代方法计算渗透系数、降深修正后井孔的影响半径和孔径为91 mm时的影响半径。具体步骤如下:首先初步确定K0值,代入式(2)可以求出R1,再将R1代入式(1)得到K1,之后再将得到的K1值代入式(2)得到R2,将得到的R2代入式(1)……直到K和R不再发生变化即可结束迭代,此时可以确定K和R的数值。将R孔和R91进行等效处理为R,应用下式(3)进行流量的换算便可得出单位涌水量。

(3)
式中:Q91、R91、r91分别为孔径为91 mm时的涌水量、影响半径和钻孔半径;Q孔、R孔、r孔分别为经过降深修正后井孔的稳定抽水量、影响半径和钻井半径。
1.2 改进的计算方法
1.2.1 井径与影响半径修正
为了能够分别获得R孔和R91,需要对抽水试验3次降深的实测数据分别进行迭代换算出井径为91 mm时的Q-S数据。迭代计算的方法如下:
(1)第一步,根据抽水试验1次降深获得的Q1和S1,另外初步假定含水层的渗透系数为K0,代入式(2)可以求出R孔-0,再将R孔-0代入式(1)得到K1,之后再将得到的K1值代入式(2)得到R孔-1,将得到的R孔-1代入式(1)……直到K和R孔不再发生变化即可结束迭代。此时可以确定K和R孔的数值。
(2)第二步,如果井径修正为91 mm,由于含水层渗透系数不变,但井径变小,致使出水能力变弱。在相同流量下,井径降深便会增加。降深增加致使降落漏斗变大,从而影响半径增大。此时已知渗透系数、抽水井流量、含水层厚度和井径,采用迭代法求取孔径为91 mm时的涌水量的影响半径和孔径为91 mm时的降深。首先初步假定S91-0,代入式(2)得到R91-0,再将R91-0代入式(1)得到S91-1,之后再将得到的S91-1值代入式(2)得到R91-1,将得到的R91-1代入式(1)……直到S91和R91不再发生变化即可结束迭代。得到S91和R91的数值。
(3)第三步,应用式(3)进行流量的换算。将上述得到的值代入式(3)即可得到井径修正后的流量。此时便将实际钻孔的Q-S数值换算成井径为91 mm时的Q-S数据。
上述步骤是对1次降深得到的Q-S数据进行换算,所以需要进行3次上述操作,将3次抽水试验实际Q-S数据换算成井径为91 mm时的数据。
1.2.2 降深修正
根据上述换算方法可得出井径为91 mm时3次降深的抽水试验数据,利用最小二乘法或图解法确定Q-S曲线的类型。本研究采用MATLAB软件进行Q-S曲线的拟合,获取得到拟合效果最好的数学关系式,之后进行单位涌水量的计算和含水层富水性的评价。
2 实例分析
本研究采用李超峰等[9]在亭南矿区进行抽水试验的数据,如下表1展开单位涌水量换算的实例分析。

表1 亭南矿区2-1水文孔抽水试验数据表
2.1 传统计算方法
2.1.1 Q-S曲线拟合
本研究采用MATLAB软件进行Q-S曲线拟合,拟合步骤是首先将三组抽水试验数据输入到MATLAB的工作区,之后调用cftool曲线拟合工具箱,在Curve Fitting Tool窗口中把对应的 x(Q) 、y(S)代入,使用Fitting进行曲线拟合。最终生成拟合曲线和参数结果。通过对上述参数的综合分析可以确定最佳拟合的曲线,进而确定曲线的方程,计算降深为10 m时钻孔的流量。
采用MATLAB软件分别进行直线型、抛物线型、对数型和幂函数型四种曲线形态进行拟合得出图1。

图1 传统计算方法的MATLAB拟合曲线图
根据MATLAB软件获取得到的四种曲线类型拟合效果参数结果统计得到表2,四种曲线类型拟合方程参数见表3。可见,抛物线型和幂函数型的拟合效果更好,因此在进行单位涌水量的换算时使用抛物线型和幂函数型进行计算。

表2 传统计算方法的曲线拟合效果表

表3 传统计算方法的曲线类型拟合参数表
2.1.2 井径换算
迭代方法的计算步骤详见1.1.2,此时我们将R孔≈R91采用Excel软件可以节省计算时间,其计算精度也可以保证。采用Excel进行的迭代计算结果如表4。
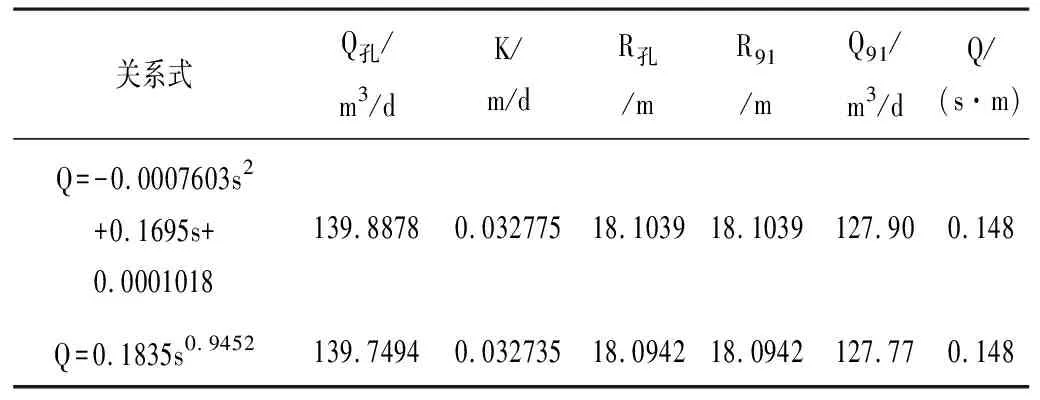
表4 传统计算方法的井径换算计算表
根据表4的数据可知,抛物线型和幂函数型得出的单位涌水量的数值在保留小数点后三位的情况下是一致的,为0.148。
根据《矿区水文地质工程地质勘探规范》[1]、《煤炭矿井防治水设计规范》[2]的规定,按单位涌水量q划分含水层富水性标准见表5。结合表5的含水层富水性划分表可知,该区属于中等富水性。

表5 含水层富水性划分表
2.2 改进的计算方法
2.2.1 井径换算
根据抽水试验的三组数据,采用1.2.1的步骤进行迭代计算,此时将R孔和R91的数值分开计算得到表6。

表6 更正计算方法的井径换算计算表
2.2.2 降深换算
同样采用2.1.1的方法进行Q-S曲线的拟合,分别进行直线型、抛物线型、对数型和幂函数型四种曲线形态进行拟合得出图2。

图2 更正计算方法的MATLAB拟合曲线图
根据MATLAB软件获取得到的四种曲线类型拟合效果参数结果统计成表7,四种曲线类型拟合方程参数见表8。

表7 更正计算方法的曲线拟合效果表

表8 更正计算方法的曲线类型拟合参数表
根据表8可知,抛物线型的拟合效果相对更好,即Q=-0.008 987S2+11.35S-0.021 85。将S=10 m代入式中可知Q=112.579 5 m3/d。换算成单位涌水量即q=0.130 3 L/(s·m)。根据表5可知,该区属于中等富水性。
2.3 误差分析
通过系列的计算,我们得出传统的换算方法计算出的单位涌水量为0.148 L/(s·m),而改进过后的方法计算出的单位涌水量为0.130 3 L/(s·m) ,其相对误差为12%。结果分析表明两种计算方法存在一定的差异,因此有必要在单位涌水量换算过程中考虑影响半径差异带来的误差。
3 结语
本文利用抽水实验数据,采用两种不同的方法对含水层单位涌水量进行计算,分析影响半径变化对计算结果误差的影响,得出以下结论。
(1)单位涌水量是评价含水层富水性的重要指标,改进的单位涌水量换算方能够分别计算出R91和R孔,这对单位涌水量的准确计算提供了一定的理论支撑。
(2)本研究采用Excel软件展开迭代计算,使用MATLAB软件进行Q-S曲线的拟合得出单位涌水量的结果。该方法可以合理地找到最佳曲线类型,并计算结果的精度能够得到保证。
(3)在讨论分析传统计算方法和更正后的方法时,两者计算结果对比发现存在一定的差异,因此有必要在单位涌水量换算过程中考虑影响半径差异带来的误差。
