基于叠加理论的柱热源模型岩土体热响应试验测试研究

2024-03-08郭华

地下水 2024年1期

郭华

(江苏省地质环境勘查院,江苏南京 211100)

0 前言

浅层地温能是指蕴藏在地表以下一定深度范围内(一般200 m)的岩土体、地下水中具有开发利用价值的地热能,是一种可再生的新型环保能源,开发利用浅层地温能对促进国家节能减排和实现碳达峰、碳中和目标具有非常重要的意义。浅层地热能的利用,主要是通过热泵技术的热交换方式实现,目前利用的地源热泵技术种类主要为地埋管地源热泵系统。热导率和每延米的换热量等岩土热特性参数是地埋管地源热泵系统设计需要的重要参数,目前岩土热物性测试方法主要有探针法、岩土类型判别法、稳态测试法和现场热响应试验测试法。探针法由于其测量的土壤范围较小,测试结果仅代表探针周围一小部分岩土体热物性参数值,不能代表整个换热孔周围岩土体的参数值。岩土类型判别法是根据岩土体类型确定其热物性参数最直接的方法,由于岩土体结构的复杂性和差异性,热物性参数受沉积环境、水文地质条件等多种因素影响,这种方法得到的参数值误差较大,并且沿钻孔深度岩土体类型较多,想得到整个钻孔范围内热物性参数也是相当困难的。稳态测试法对采集到的岩土体样品进行室测内测定时,样品受到扰动其结构发性了很大的变化,测得的参数误差较大。现场热响应试验测试法克服了上述方法的局限性,提高了热导率和每延米的换热量等参数测试的准确度。

现场热响应试验测试数据分析模型方法多样,但大多模型由于过于粗糙,回避了U型管与钻孔间产生的传热干扰问题,从而无法处理因U型管各支管间的传热对整个换热过程的影响,导致计算结果精度较差。本文阐述了基于叠加理论的柱热源传热模型,该模型考虑了钻孔直径大小的影响,采用该方法对测试数据进行分析处理,得到岩土热物性参数更符合实际。

1 试验原理

以恒定热流法为例,现场热响应试验过程为:首先,将测试仪的水路循环部分与待测换热器相连接,形成一个闭式环路;然后,通过启动管道循环水泵,以驱动环路流体开始循环。待系统进出口温差为零时,开始启动电加热器来加热环路中的流体。随着换热器进口水温的不断升高,其热量通过管壁与土壤之间的传热过程逐渐释放到地下土壤中,同时使土壤温度也逐渐升高,最终管内流体温度和土壤温度维持在一种动态的热平衡状态。然后,增大加热功率,系统将重复上述传热过程,直至达到新的平衡状态。在整个流体加热循环过程中,通过计算机采集系统记录进/出管内流体温度、流量和加热功率等参数,与此同时地下温度的变化情况也会自动记录下来。

通过现场热响应试验模拟冬、夏季热泵实际运行工况,测量进/出仪器的流量、进/出温度和时间,依据不同负荷测试,最终求得:换热孔的热导率、每延米吸热量和排热量(W/m)。

现场热响应试验在理论上可以归结为在一定热流边界条件下的非稳态传热问题(图1)。其数学解析主要有两种模型:1)基于线热源理论的线模型;2)基于圆柱热源理论的柱模型。线热源理论模型在热响应试验测试中的应用研究较多,而柱热源数学模型在现场热响应试验中的应用研究较少。

图1 现场热响应试验测试原理图

2 数学模型

地埋管地源热泵现场热响应试验分析地埋管与岩土体的传热过程可分为两部分,即换热孔内的传热过程和换热孔外的传热过程。由于换热孔尺寸和回填材料热容都较小,可以很快达到热量相对平稳的过程,因此,换热孔内的传热过程可按稳态传热过程处理。换热孔壁以外区域为无限体,按非稳态传热过程处理。

2.1 基于柱热源理论的换热孔外传热数学模型

将地埋管在岩土体中连续导热假定为一恒定热源,忽略换热介质流体沿深度方向上的热量交换,则地埋管与周围岩土体间的导热过程可以假定为一维圆柱型热传导问题,可按非稳态传热过程处理,其数学模型为:

(1)

式中:T为换热孔深度范围内岩土体温度,℃;t为换热时间,s;db为换热孔直径,m;λs为换热孔周围岩土体的导热系数,W/(m·K);cs为岩土体平均比热容,J/(kg·K);ρs为换热孔深度范围内岩土体质量密度,kg/m3;T0为未受扰动的岩土原始温度,℃;r为计算点至柱热源中间距离,m。

根据边界条件和初始条件,对式(1)进行积分获取换热孔影响范围内岩土体温度,其数学表达式为:

(2)

式中:ql为地埋管单位长度换热量,J/m。

f(x)为计算岩土体温度的指数函数,其数学表达式为:

(3)

当地埋管地源热泵系统加热时间较长,at/r2≥5时,可得,

(4)

式中:γ为欧拉常数,且γ=0.577 2。

则式(2)可简化为

(5)

式(5)建立了换热孔深度范围内岩土体温度与未扰动土层温度之间的关系,但更有意义的是掌握地埋管地源热泵系统运行过程中换热孔深度范围内岩土体温度随换热介质流体温度变化情况。

当r=db/2时,换热孔壁处岩土体温度为:

(6)

2.2 基于叠加理论的换热孔内传热数学模型

忽略换热介质流体沿深度方向上的热量交换及换热孔轴向导热影响,基于叠加理论的数学模型考虑了换热孔内U型管几何配置及两支管间因温度差而产生的温度干扰现象,更符合换热孔内的实际传热情况。以单U型地埋管为例,设单U型管中下行和上行支管内换热介质流体的温度分别为T1、T2,q1、q2分别为下行和上行支管换热量,R1、R2分别为下行和上行支管内换热介质流体与换热孔壁间的热阻,R12、R21为两支管间热阻,根据叠加理论,换热孔内两支管与换热孔壁间热传导数学模型为:

(7)

通常现场热响应试验换热孔内U型管是对称分布,则有R1=R2,R12=R21。

(8)

(9)

式中:Rp、Rf分别为地埋管管壁传热热阻和管壁与换热介质流体间产生热阻,则有:

(10)

(11)

式中: di、do为U型管内、外径,m;2D为单U管两支管中心距,m;λb为回填材料导热系数,W/(m·K);λs为地埋管垂向范围内岩土体导热系数,W/(m·K);λp为试验管管壁材料导热系数,W/(m·K);α为换热介质流体与换热管内壁间的对流传热系数,W/(m2·K)。

根据规范要求地埋管内换热介质流体应保持紊流态,流速不宜小于0.4 m/s。则管内换热介质流体雷诺数和普朗特数分别为:

(12)

(13)

式中:u为换热介质流速管内流速,m/s;ρ为换热介质流体密度,kg/m3;μ为换热介质流体动力粘度系数,Pa·s;λw为换热介质流体导热系数,W/(m·K);cp为换热介质流体比热容,J/(kg·K)。

地埋管地源热泵运行过程中,换热介质流体一般为清洁的自来水,循环温度30℃左右,则水的物理参数分别为:ρ=1×103kg/m3;μ=0.800 7×10-3Pa·s;λw=0.62W/(m·K);cp=4.17×103J/(kg·K);地埋管内径di一般为26 mm。

根据式(12)、(13)可计算出管内换热介质流体雷诺数和普朗特数。

当雷诺数Re>10 000时,管内换热介质流体达到旺盛湍流状态,由迪图斯-贝尔特公式,换热介质流体与换热管内壁间的对流传热系数计算表达式为:

(14)

式中:当地埋管地源热泵运行过程中制热时,n=0.4,制冷时,n=0.3。

由于换热孔尺寸和回填材料热容都较小,可以很快达到热量相对平稳的过程,因此,换热孔内的传热过程可按稳态传热过程处理。则有:

假设换热孔壁处温度为Tw,则T1=T2=Tw,式(7)可进一步简化为:

(15)

式中:R0为考虑支管相互干扰时换热孔内总热阻。

2.3 数学模型偶合分析

地埋管换热系统运行过程中,换热孔内可假定为稳态传热过程,换热孔外为非稳态传热过程,根据式(6)和式(15)可以把换热孔内、外传导过程进行偶合,获得地埋管内换热介质流体平均温度与换热孔内总热阻间相互关系。即:

(16)

采用恒定热流法进行现场热响应测试时,单位长度换热量ql恒定,对于待测定的钻孔和地埋管来说,其余均为定值,则只有lnt一个变量,于是可将式(15)简化为一个二元一次线性方程:

Tw=mlnt+b

(17)

(18)

(19)

(20)

式中:Tg,in为地埋管进水温度,℃;Tg,out为地埋管出水温度,℃。

通过现场热响应试验测得ql及不同时间段地埋管换热介质流体平均温度Tw值,在温度-时间对数坐标系中拟合出式(17),从而得出m、b的值,由式(19)(21)、(22)可分别计算出岩土体综合导热系数λs、体积比热容ρscs和换热孔内总热阻R0:

(21)

(22)

Cv=ρscs

(23)

3 工程应用

3.1 工程背景

“江苏省宿迁沭阳城区浅层地温能资源调查与开发利用研究”项目进行了3组现场热响应试验测试,其中以HRK1号孔试验来说明上述模型的工程应用原理。HRK1号孔设计换热孔深98.7 m,埋管类型为DN32单U型,采用砂回填。采用了恒定热流法试验测试。换热孔及地埋管相关参数详见表1。

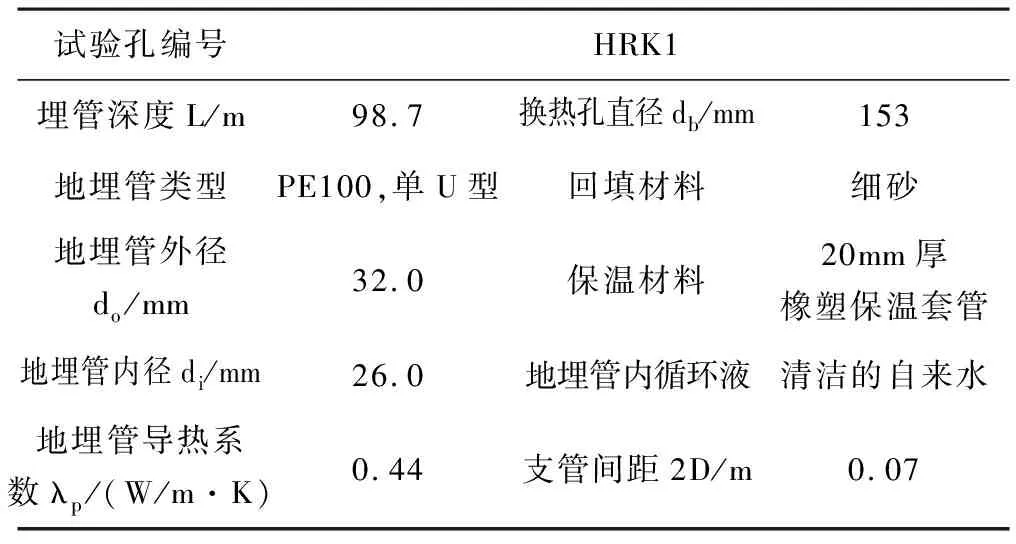
表1 换热孔及地埋管的相关参数

3.2 试验过程

3.2.1 岩土体初始平均温度测试

为获取岩土体初始平均温度,试验开始前进行无功循环,连接测试仪器和地埋管,开启循环水泵,在不加热且不制冷的情况下驱使地埋管中的水循环,至进出水口温度稳定,取稳定段地埋管回水温度作为岩土初始平均温度,测试曲线如图2。

图2 岩土初始平均温度曲线

从图2上可以看出,840min之前,管内温度比较平稳,之后受天气等因素的影响,管内温度有所上升,取稳定段的温度值,即19.80℃。

3.2.2 恒定热流法测试

岩土体初始平均温度完成后,此时换热介质流体与岩土体传热过程达到平衡,对试验孔进行了“恒定热流法”测试,测试过程中采集加热功率、平均流量、地埋管进出口温度等数据。图2为加热功率、温度及流量的随测试时间变化趋势图。热响应试验开始阶段,传热过程主要集中在换热孔内,由于换热介质流体、地埋管和回填材料热容量较小,地埋管进、出口温度迅速上升。随着试验进行,10 h后,换热孔内热量向外扩散至周围岩土体中,地埋管进、出口温度逐渐达到平衡,趋于稳定状态。稳定状态下测试参数如表2所示。

表2 现场热响应试验采集参数一览表

实际平均加热功率为3 829 W,平均流量为1.30 m3/h(流速为0.68 m/s),测试设备连续加热,每隔3 min记录一次地埋管进、出水温度及流量数据,以获取岩土综合导热系数。图3为加热功率、温度及流量的测试曲线,图4为地埋管进出水平均温度对数拟合曲线。

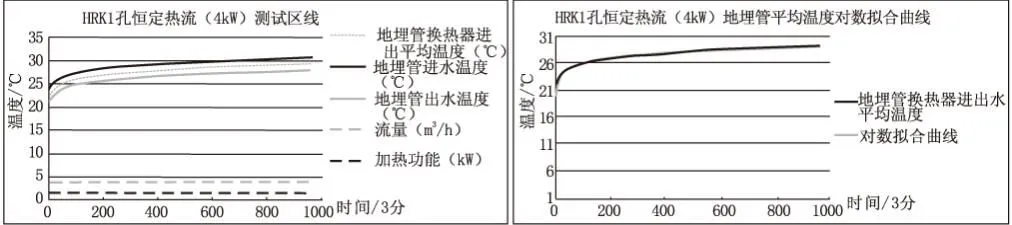
图3 恒定热流(4 kW)测试曲线图

3.2.3 曲线拟合分析

根据数学模型,地埋管换热介质流体进出口平均温度与测试时间对数成线性关系,拟合曲线如图3所示。拟合曲线的斜率m=1.329,截取b=19.927,由式(20)、(21)、(22)计算出该试验条件岩土综合导热系数λs为2.32 W/(m·K),体积比热容为1.42×103J/kg·K,换热孔内总热阻R0为0.125(m·K)/W。