悬挂胶轮列车与钢桥的振动试验及仿真研究
2024-03-08李奇,吕超,李黎
李 奇,吕 超,李 黎
(1.同济大学土木工程学院,上海 200092;2.西藏农牧学院,西藏林芝 860000;3.中铁第六勘察设计院集团有限公司桥梁设计院,天津 300308)
1901 年德国建成并运营第一条悬挂式单轨线路,随后悬挂式单轨交通线在日本等国家得到了推广应用。悬挂式单轨交通具有地形适应能力强、建设周期短、占地少、运行噪声低、观光功能佳等诸多优点,在山地和旅游交通上具有良好的应用前景[1-2]。为了确保悬挂式单轨交通系统的平稳运行,并为轨道梁桥设计提供合理参数参考,需要进行现场试验和动力仿真研究。近年来,我国也开始进行悬挂式单轨的应用研究,建成了多条悬挂式单轨交通试验线,并对轨道梁结构进行了静动力性能研究[3-5]。
在悬挂式单轨车桥耦合振动方面,胡晓玲[6]基于日本的悬挂式单轨车辆结构形式,建立了动力学模型,研究了在不同线路时车辆的运行状况;曾令会等[7]对日本和德国两种悬挂式单轨列车的动力性能进行了对比研究;陈志辉[8]建立了悬挂式单轨的拓扑模型,并将仿真结果与试验结果进行了对比;何庆烈等[9]开展了悬挂式单轨的试验研究,表明悬挂式单轨在运行时有良好的平稳性;李靖等[10]结合有限元软件、多体系动力学软件和计算流体动力学软件进行了风荷载作用下悬挂式单轨系统车桥耦合振动分析。
由于既有研究缺乏对悬挂式单轨车、桥系统参数和动力响应的系统测试和仿真研究,本文以河南开封悬挂式单轨交通示范线为背景,利用专为悬挂式单轨开发的橡胶列车-钢轨道梁桥耦合振动分析程序,根据实际现场测得的车辆力学参数,建立了悬挂式单轨列车-轨道-桥梁系统的耦合振动模型。通过与实际现场测得的车桥动力响应的一致性,验证了动力计算模型的自编仿真软件的正确性。最后,根据仿真软件结果和相应规范,评价了悬挂式单轨列车的走行性能以及轨道桥梁的竖向和横向刚度,并对列车运营和桥梁结构设计的参数和评价指标提出了建议。
1 车桥耦合振动模型及计算方法
图1 为悬挂式单轨车桥系统示意,为进行系统耦合振动仿真分析,需对车辆、桥梁、轮轨接触、不平顺等建模,并采用合适的方法进行系统响应求解。
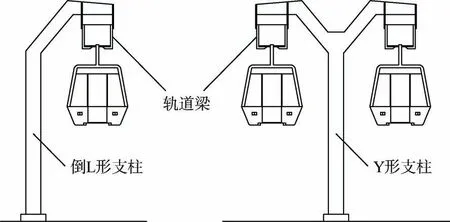
图1 悬挂式单轨系统结构示意Figure 1 Structure of suspended mono-rail system
1.1 车辆模型
每节悬挂式单轨车辆由车体和前、后转向架共3 个刚体组成,两个转向架及车体的质量、刚度和转动惯量分别集中在3 个节点上,转向架与车体之间通过单元连接。每个刚体各包含沉浮、点头、侧移、摇头、侧滚共5 个自由度,整个模型共计考虑15 个自由度。由于悬挂胶轮车辆构造有别于传统钢轮列车,模型中空气弹簧、轮胎及锥形弹簧等构件的力学参数由现场试验测定。建立的悬挂式单轨胶轮车辆动力计算有限元模型如图2 所示。

图2 悬挂式单轨胶轮车辆模型Figure 2 Model of rubber-tire suspended mono-rail vehicle
1.2 桥梁模型
开封悬挂式单轨交通示范线全长约1.176 km,全线均采用简支桥梁结构。直线段轨道梁主要采用25 m跨度,曲线段轨道梁主要采用12 m 和16 m 两种跨度;平曲线共设3 处,半径分别为30、50 和500 m;最大纵坡4.7%。轨道梁和桥墩均采用钢结构,基础采用钻孔灌注桩。轨道梁采用底面开口钢箱梁,箱梁内腔净高1 100 mm,净宽780 mm,直线梁腹板、顶板和底板厚度分别为24 mm、24 mm 和32 mm,钢材型号为Q345qD。单线桥墩为倒“L”形钢结构,其等截面段构造尺寸为800 mm×800 mm×28 mm,材料为Q345D。为考虑最不利状况,选取直线段和半径为30 m 曲线段单线轨道梁桥进行车桥系统耦合振动响应现场试验和动力仿真分析。
梁单元模型建模简单、计算效率高,能够反映桥梁整体振动的特性。为对比桥梁模型对仿真结果的影响,针对直线段的5 跨桥梁分别建立梁单元和板壳单元动力计算模型,频率结果见表1。经过对比,验证了板壳单元模型体系与梁单元模型体系是一致的,由于板壳单元反映的频率数量更加丰富,计算更加精确,选用板壳模型(见图3)的仿真结果与实测结果进行对比分析。
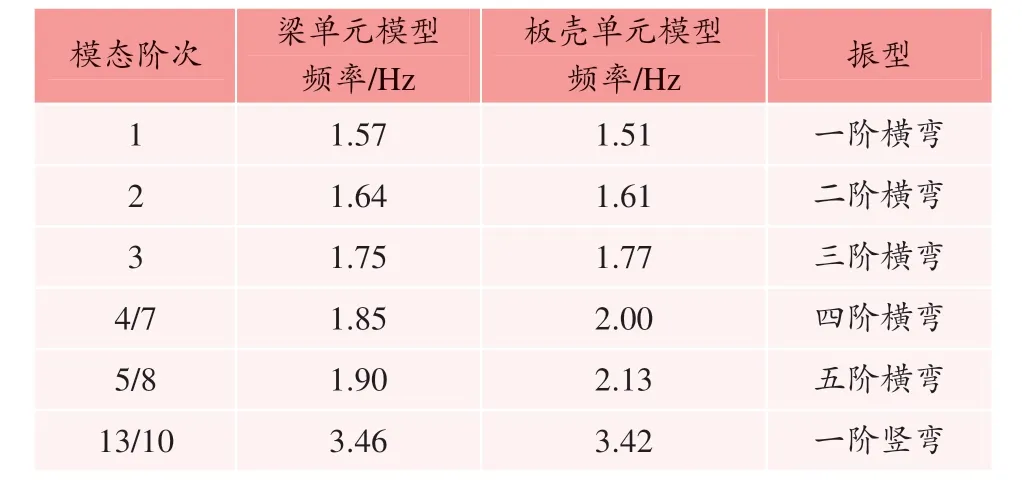
表1 板壳与梁单元模型模态振型对比Table 1 Comparsion of model shapes obtained from shell and beam models

图3 悬挂式单轨桥梁板壳有限元模型Figure 3 Shell-element model of mono-rail bridge
1.3 轮轨耦合关系
悬挂式单轨车辆与传统铁路车辆的轮轨耦合处理方法基本相同,但细节有所不同。悬挂式列车的走行轮仅提供竖向力,而导向轮仅提供横向力,则每个走行轮所受的由轨道梁作用的竖向力为
式中,kv、cv分别为走行轮的竖向刚度和阻尼系数;yrv、ybv和ywv分别为轨道梁走行面高低不平顺、走行轮下的轨道梁竖向位移和该走行轮的竖向位移;符号“.”表示对时间的导数,即速度。
同理,每个导向轮所受的横向力可表达为
式中,下标“l”表示横向,其他符号意义与式(1)相同。
1.4 不平顺输入
图4 为某存在异常振动的悬挂式单轨试验线上采用3D 激光扫描法测试分析得到的轨行面不平顺功率谱与国外相关成果对比。从图4 可看出,该悬挂式单轨交通试验线轨行面实测不平顺功率谱比日本一跨坐式单轨桥梁实测结果略大,与ISO 8608 A级路面相近。由于开封试验线线路平顺性较好,故计算中参考日本单轨桥梁的实测功率谱函数[11]:

图4 某悬挂式单轨不平顺实测功率谱与国外相关结果对比Figure 4 Comparison of measured irregularity power spectrum of mono-rail system and related results abroad
式中,S(Ω)为轨道梁行车表面不平顺的功率谱密度函数;Ω为空间频率(cycle/m);α、β、n为不平顺系数。实际不平顺波长范围很广,但可测试的波长范围有限,考虑波长范围为0.4~100 m,充分激发系统中低频振动,根据式(3)模拟得到轨行面高低不平顺样本。
1.5 车桥耦合振动求解方法
采用模态叠加法求解车桥耦合振动响应。列出车辆在模态坐标下的运动微分方程[12]:

式中,各变量含义与车辆运动方程相类似,下标b 代表桥梁。
由式(4)和式(5)可知,车辆和桥梁运动微分方程的左端均由模型的频率、振型和模态阻尼比决定,右端均由轮轨力、虚拟力和其他外力组成。采用龙格库塔法求解车桥耦合振动方程式(4)、式(5),即可得到车辆与桥梁的动力响应。
2 现场试验及仿真计算结果
2.1 现场试验概况
为获取车桥耦合计算所需的关键参数,并验证车桥耦合振动仿真计算结果,依托开封悬挂式单轨交通示范线开展了现场试验,包括车辆力学参数以及车辆和轨道梁桥动力响应测试,试验工况为列车以不同速度(5~40 km/h)匀速通过和制动。
测试列车采用2 节编组,在前节车厢地板的车头、车中、车尾以及后节车厢地板的车头各布置1 处横、竖向加速度测点,布置位置信息见表2,其中前节车厢的各测点分别布置了压阻式加速度传感器以及智能手机(内置三轴加速度计)测取车体加速度时程,后节车厢的测点布置了智能手机。前节车厢车头的加速度测点如图5 所示。压阻式加速度传感器采样频率为1 000 Hz,智能手机采样频率为50 Hz。

表2 车体传感器编号及说明Table 2 Number and description of sensors in car-body

图5 前节车厢地板布设的加速度测点Figure 5 Measurement position of acceleration on floor of front vehicle
分别在跨径为25 m 的直线段和半径为30 m 的曲线段(跨径为12 m)各一跨桥跨进行轨道梁桥振动响应测试,两个桥跨分别在支点、跨中截面布置动力响应测点,采样频率为1 000 Hz。桥跨位置图选取具体信息见表3,图6 为测点布置示意,图中测点编号的字母A、D、S 分别代表加速度、位移及应变。
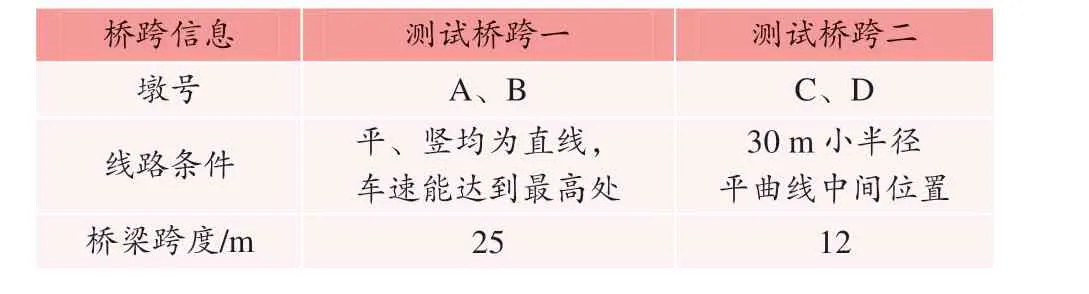
表3 测试桥跨选择Table 3 Test bridge-span selection
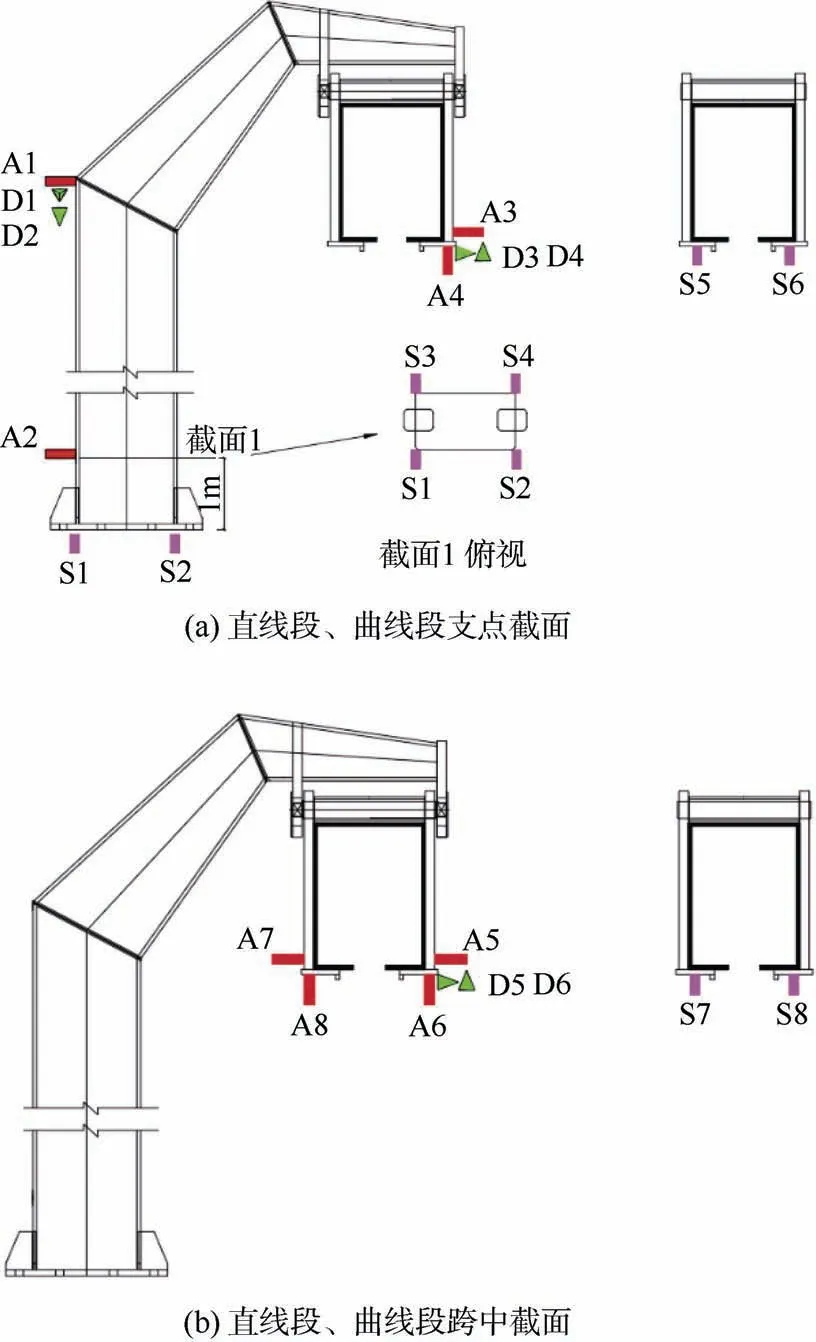
图6 测试桥跨动力响应测点布置示意Figure 6 Arrangement of measurement positions of dynamic responses at tested bridge spans
2.2 车辆参数测试
2.2.1 空气弹簧刚度及阻尼
将车体视为刚体,则车体竖向响应仅由沉浮与点头两阶模态构成。以40 km/h 速度工况为例,通过4号手机采集车体竖向加速度,结果如图7 所示,取制动后的余振部分时程曲线做时频转换,得到图8 的频谱图。分析车体竖向余振加速度频谱,获取车体沉浮与点头振型的频率;联立这两阶振型的模态振动方程,即可求得单个空气弹簧的竖向刚度k1z及车体的竖向转动惯量Icz;利用对数衰减率计算响应频率的阻尼比,即可求得单个空气弹簧的竖向阻尼系数C1z。同理可得单个空气弹簧的横向刚度k1y、横向阻尼系数C1y及车体的横向转动惯量Icy。测试分析结果列于表4。

表4 车辆空气弹簧参数测试结果Table 4 Test results for parameters of vehicle pneumatic springs
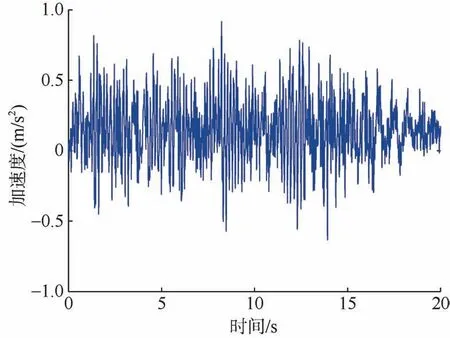
图7 车速40 km/h 时车体竖向加速度时程Figure 7 Time-history of vertical acceleration of car-body at 40 km/h

图8 车速40 km/h 时车体竖向加速度频谱Figure 8 Vertical acceleration spectrum of car-body at 40 km/h
2.2.2 空气弹簧刚度及阻尼
在车辆静止状态下,分级向车厢内堆载、卸载,用激光位移计测得各级荷载变化时走行轮、转向架的竖向位移变化量(见图9),继而计算得到单个走行轮的竖向刚度及锥形弹簧的竖向刚度。

图9 车辆竖向位移测量Figure 9 Measurement of vertical displacement of vehicle
通过多组实验测得荷载变化量和左、右轮轮胎处位移变化量及锥形弹簧变形量,求得悬挂式胶轮车辆的轮胎及锥形弹簧的刚度,分别为16.8 MN/m 和24.3 MN/m。
2.3 车桥动力特性
2.3.1 车辆
表5 为悬挂式胶轮车辆前5 阶自振频率的理论计算与现场实测值。由图可知,理论与实测值基本一致,车辆模型和参数可靠。

表5 悬挂式胶轮车辆自振频率Table 5 Natural frequencies of rubber-tire suspended vehicle
2.3.2 轨道梁桥
直线段轨道梁桥动力特性见表6。
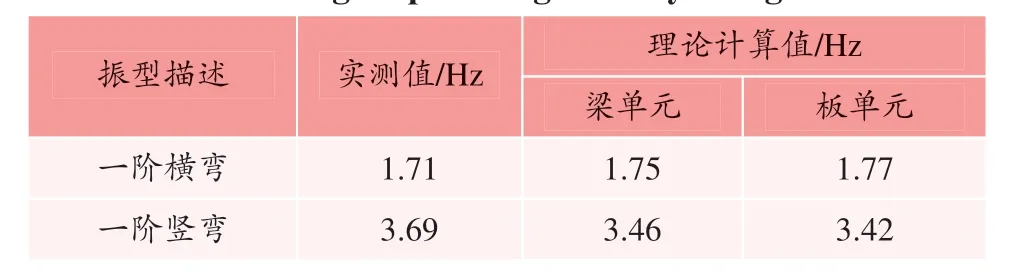
表6 直线段轨道梁桥竖、横向基频Table 6 Vertical and lateral natural frequencies of straight spans of guideway bridge
由表6 可知,轨道梁桥横、竖向基频现场实测值与理论计算值基本吻合。梁单元和板壳单元模型计算的轨道梁桥竖、横向挠曲基频非常接近;轨道梁桥的横向挠曲频率明显低于竖向频率,可知桥梁结构横向刚度明显小于竖向刚度。
2.4 车辆响应
列车分别以40、20 km/h 速度通过直线和曲线段桥梁时,经40 Hz 低通滤波的车体加速度时程分别如图10~11 所示。
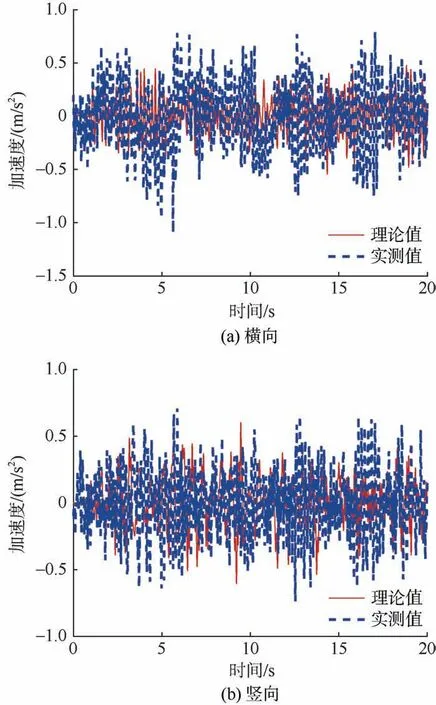
图10 列车以40 km/h 速度通过直线段桥梁时的车体加速度时程曲线Figure 10 Time-histories of acceleration of car-body while passing straight spans at 40 km/h
综合图10、图11 可知,列车车体竖向振动加速度动力仿真与实测结果基本吻合;车体横向振动加速度动力仿真与实测值偏差稍大,其主要原因是动力仿真时未考虑侧风[10]等外界因素导致的车身低频摆动。
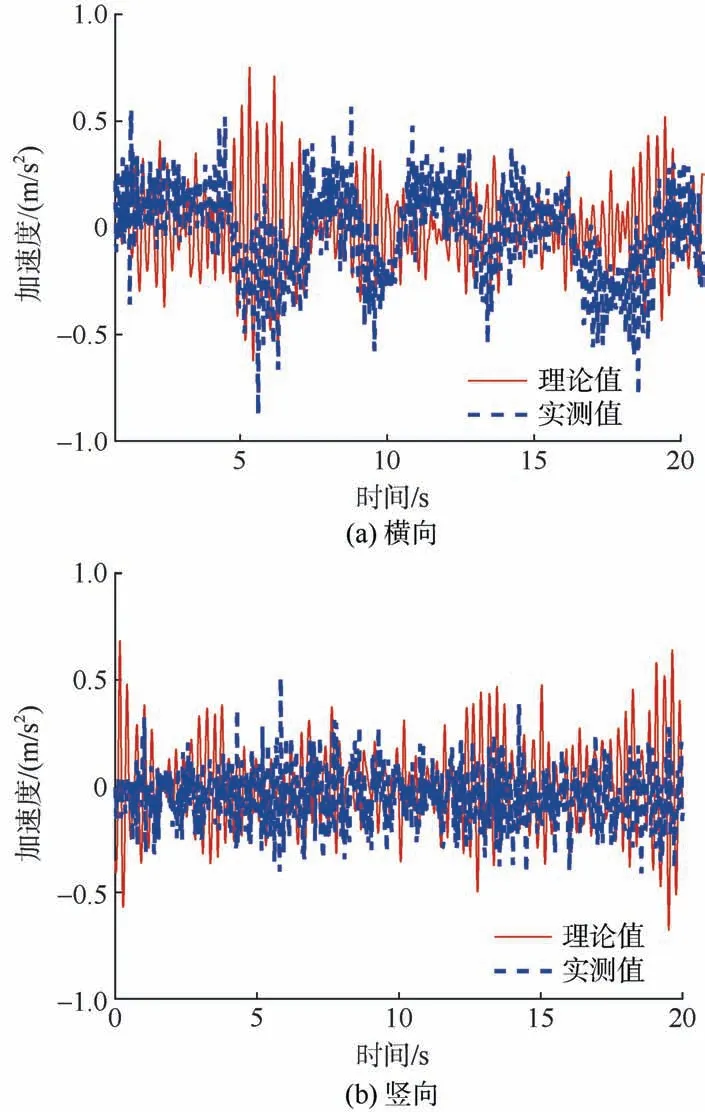
图11 列车以20 km/h 速度通过曲线段桥梁时的车体加速度时程曲线Figure 11 Time-histories of acceleration of car-body while passing curved spans at 20 km/h
2.5 轨道梁桥响应
2.5.1 竖向位移
采用视频跟踪标记点的方法测试钢轨道梁桥的竖向位移。图12 为列车以40 km/h 速度通过直线段时,轨道梁支点处D4及跨中截面D6 测点的竖向动位移时程曲线。
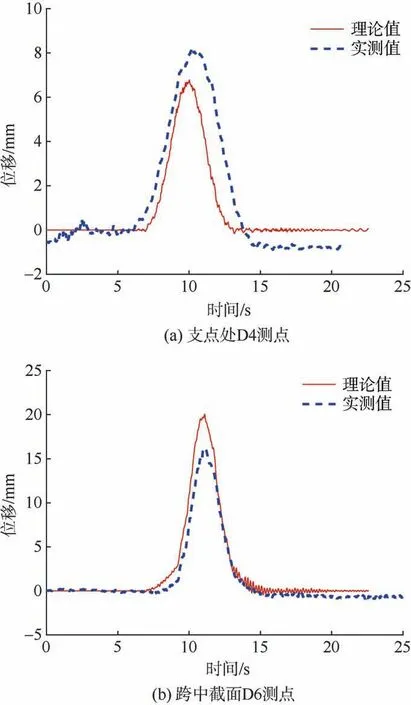
图12 列车以40 km/h 速度通过直线段桥梁时轨道梁竖向位移时程曲线Figure 12 Time-histories of guideway displacement while passing straight spans at 40 km/h
分析图12 可知,列车通过时,轨道梁的竖向位移动力仿真与实测时程规律相同,但有一定的偏差,主要原因是现场风荷载的影响,且动力仿真时未考虑桥墩基础弹性的影响。
2.5.2 应力
图13 为列车以40 km/h 速度通过直线段时,桥墩距墩底1 m 截面角点S4 和轨道梁跨中底部内侧S7 测点轴向应力时程曲线。从图13 可看出,列车通过时,桥墩和轨道梁轴向应力的理论计算与现场实测结果基本吻合。

图13 列车以40 km/h 速度通过直线段桥梁时桥墩及轨道梁轴向应力时程曲线Figure 13 Time-histories of stress of pier and guideway while passing straight spans at 40 km/h
综上可知,采用自编软件计算的悬挂式单轨胶轮列车和钢轨道梁桥耦合振动响应与现场实测结果基本一致。
3 车桥性能评价及建议
3.1 列车走行性
3.1.1 舒适性
表7 为悬挂式单轨列车满载通过直线段轨道梁桥时,竖、横向Sperling 舒适度指标计算值及其评价等级。由表7 可知,列车在直线段行驶时,车速在50 km/h以内车辆竖、横向Sperling 舒适度指标评价等级均为“优”,当车速超过50 km/h 时竖向Sperling 指标降为“良”;列车行驶速度在90 km/h 以内,其竖、横向Sperling 舒适度指标均能达到优良标准。为确保乘客舒适度,悬挂式单轨列车在直线段轨道梁桥上行驶时速不宜超过90 km/h;如运行时速不超过50 km/h,则乘客舒适度更佳。

表7 列车满载通过直线段轨道梁桥时Sperling 舒适度指标Table 7 Sperling index with fully loaded vehicle passing straight spans
表8 为悬挂式单轨列车满载通过曲线段轨道梁桥时,车体竖、横向Sperling 舒适度指标计算值及其评价等级。从表8 可看出,悬挂式单轨列车满载通过半径为30 m 的轨道梁桥时,如运行速度不超过20 km/h,车辆竖、横向Sperling 舒适度指标均能达到“合格”要求;当速度达到30 km/h 时,车辆横向Sperling舒适度指标评价等级为“不合格”。因此,为确保乘客舒适性,列车在曲线段轨道梁桥上行驶车速不应超过20 km/h。

表8 列车满载通过曲线段轨道梁桥时Sperling 舒适度指标Table 8 Sperling index of riding comfort with fully loaded vehicle passing curved spans
3.1.2 安全性
悬挂式单轨列车通过轨道梁桥时,计算轮重减载率随车速的变化规律如图14 所示。
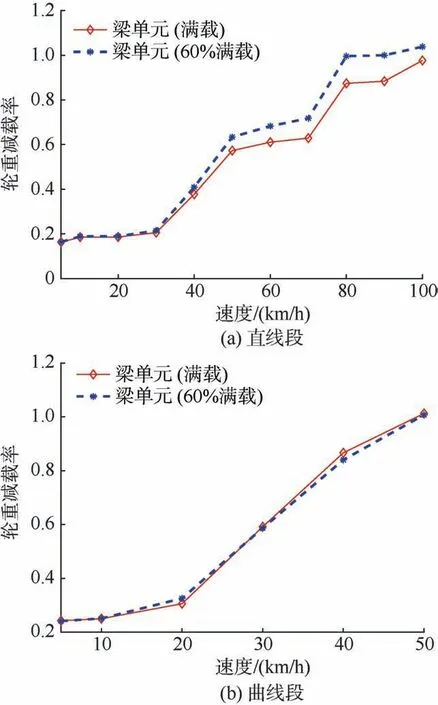
图14 列车通过轨道梁桥时的轮重减载率Figure 14 Rate of wheel load reduction of vehicle while passing guideway bridge
由图14 可知,在直线段上车速达到50 km/h、在半径为30 m 的曲线段上车速达到30 km/h 时,轮重减载率超过0.6。现行轮轨式轨道交通相关规范对轮重减载率的限制,主要是为了避免钢轮脱轨,而悬挂式单轨由于导向轮和稳定轮的构造并不存在脱轨问题,此处减载率指标有关结果仅供参考。
3.2 直线段轨道梁桥动力性能
3.2.1 结构变形
1) 轨道梁位移。采用梁单元和板壳单元模型在单轨列车满载作用下轨道梁跨中截面竖向位移计算值分别为30.3 mm 和28.8 mm,两者相差不大;将跨中竖向位移减去两边支点竖向位移的均值,得到轨道梁跨中截面竖向挠度计算值为20.8 mm,挠跨比为1/1 202,小于《悬挂式单轨交通技术标准》(DBJ41/T217—2019)规定的1/1 000 挠跨比。
2) 轨道梁梁端转角。相邻梁端的转角之和综合反映了梁体挠曲和墩体弯曲产生的影响,可作为表征墩、梁变形的综合指标。经计算,相邻两孔的梁端竖向转角之和计算值为4.3‰rad,横向转角之和为1.5‰rad。
3.2.2 动力系数
各级车速下,轨道梁跨中截面走行面处应力的动力系数如图15 所示。其中,车速40 km/h 时纵向应力动力系数的计算结果为1.07,与试验结果吻合较好。
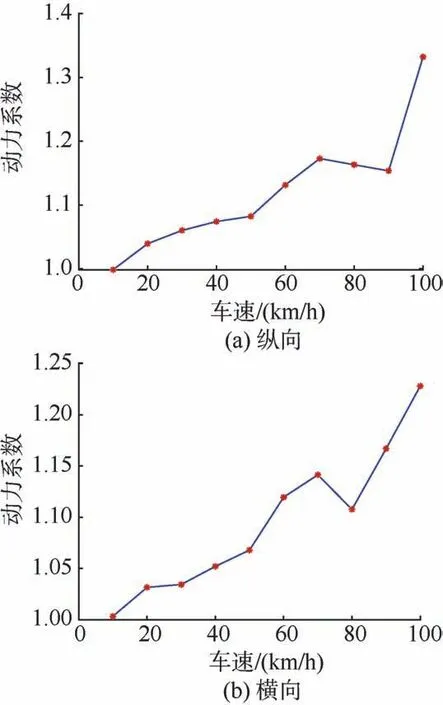
图15 钢轨道梁应力动力系数Figure 15 Dynamic factors for stress of steel guideway girder
分析图15 可知:动力系数总体上与车速呈正相关,当车速达到100 km/h 时急剧增大;当桥梁设计车速不大于80 km/h 时,轨道梁纵、横向动力系数可分别取为1.17 和1.14。
3.2.3 振动加速度
直线段轨道梁跨中截面竖、横向振动加速度幅值与车速的关系如图16 所示,其中车辆模型分别采用4 节满载(达到设计轴重4.48 t)和60%满载车厢(轴重3.86 t)两种情况。
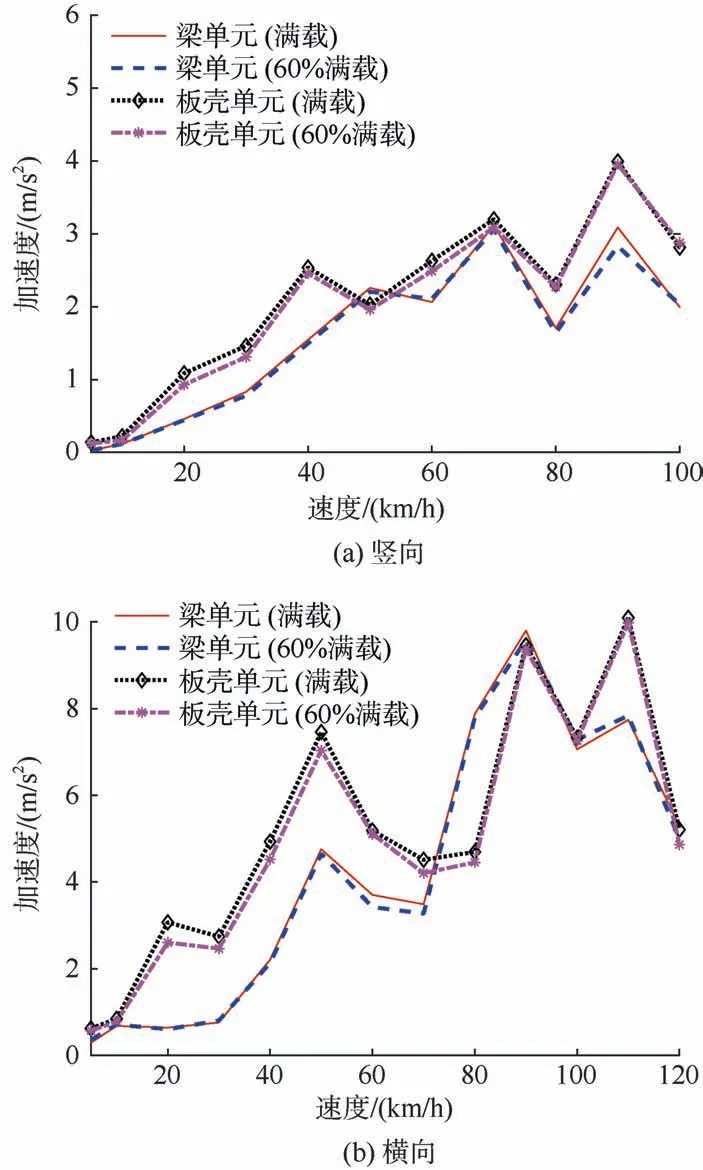
图16 轨道梁跨中截面振动加速度Figure 16 Vibrating acceleration of mid-span section of steel guideway girder
从图16 可以看出,桥梁竖、横向振动加速度总体上随着列车运行速度的提高而增大。由图16(a)可知,列车运行速度在100 km/h 以内时,轨道梁竖向振动加速度不超过《铁路桥涵设计规范》(TB 10002—2017)规定的无砟桥面不应大于5.0 m/s2(半峰值)的要求;由图16(b)可知,列车运行速度达20 km/h 时,桥梁横向振动加速度即超过了《铁路桥涵检定规范》(铁运函〔2004〕120 号)给定的“桥跨结构在荷载平面的横向振动加速度不应超过1.40 m/s2”的规定。
桥梁横向振动加速度偏大的主要原因是:其一,轨道梁桥的横向刚度较弱,同样的横向激励会引起轨道梁桥更大的横向响应;其二,悬挂式单轨交通轨道梁桥的竖、横向振动的耦合效应明显高于传统铁路桥梁,即车轮与轨道梁间的竖向激励会明显地引起轨道梁桥横向振动。因此,若仍采用1.4 m/s2的横向加速度限值来评价悬挂式单轨交通桥梁显然不合适。考虑到悬挂式单轨列车不存在因桥梁横向振动偏大而产生脱轨问题,建议可将轨道梁桥横向振动加速度限值适当提高,如可提高限值至与竖向加速度相同,以减小导向轮与轨道梁之间的横向力,降低噪声,确保车辆和桥梁处于较优良的工作状态。
4 结论
本文以开封悬挂式单轨示范线为背景,利用自行开发的悬挂式胶轮列车-钢轨道梁桥系统耦合振动分析程序,基于现场实测的参数建立了悬挂式胶轮列车-钢轨道梁桥耦合振动模型。综合仿真分析和现场实测的车桥动力响应结果,可得到以下结论:
1) 悬挂式单轨胶轮列车及钢轨道梁桥系统耦合振动响应理论与现场实测结果基本吻合,说明数值模拟悬挂式单轨胶轮列车走行性分析具有可行性。
2) 单轨列车满载作用下,25 m 跨度轨道梁的挠跨比为1/1 202,小于悬挂式单轨交通轨道梁挠跨比限值1/1 000,轨道梁的竖向刚度满足要求;墩底固定约束下,列车静活载产生的相邻两孔轨道梁梁端竖、横向转角之最大值为4.3‰和1.5‰;设计车速80 km/h内轨道梁纵、横向应力动力系数最大值为1.17 和1.14。
3) 为确保单轨列车的Sperling 舒适度指标评价等级不低于“合格”,悬挂式单轨列车在直线段运行时速不宜高于90 km/h,通过半径为30 m 曲线段运行时速不应超过20 km/h。
4) 由于悬挂式单轨的特殊构造决定了其没有脱轨的风险,相应的轮重减载率、轨道梁桥横向加速度等指标,有必要在现有轮轨式轨道交通相关规范的基础上适当放宽,合理限值有待进一步研究。
