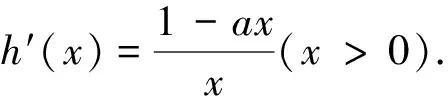图形直观引导下函数问题的分析与解决*
2024-03-08福建师范大学附属中学350007周裕燕
福建师范大学附属中学 (350007) 周裕燕
数学是研究数量、结构、变化、空间以及信息等概念的一门学科,它本身具备“形”的因素.图形能很好地直观呈现数学信息,能让一些比较隐蔽的数学结论和数学思想显现出来.很多数学问题可以通过挖掘其中的“形”,把复杂的数学问题变得简明、形象,使学生能简单、清晰地找到解决问题的思路并预测结果,避免复杂的计算和推理.
函数问题是高考重要的考查题型,不仅类型丰富,而且方法灵活,是考查学生学科核心素养和关键能力的重要载体.此类问题由于解题思路不易寻得,且求解过程较为繁琐,是学生分析与求解的难点问题.函数具备明显的“形”的特征,本文以函数中的切线、零点及偏移问题为例,阐述如果借助图形,将复杂的函数问题“直观化”,借助图形引导解题思路,揭示问题本质,并通过逻辑论证,实现问题解决.
1.运用图形直观,分析和解决函数的切线问题
例1 若过点(a,b)可以作曲线y=ex的两条切线,则( ).
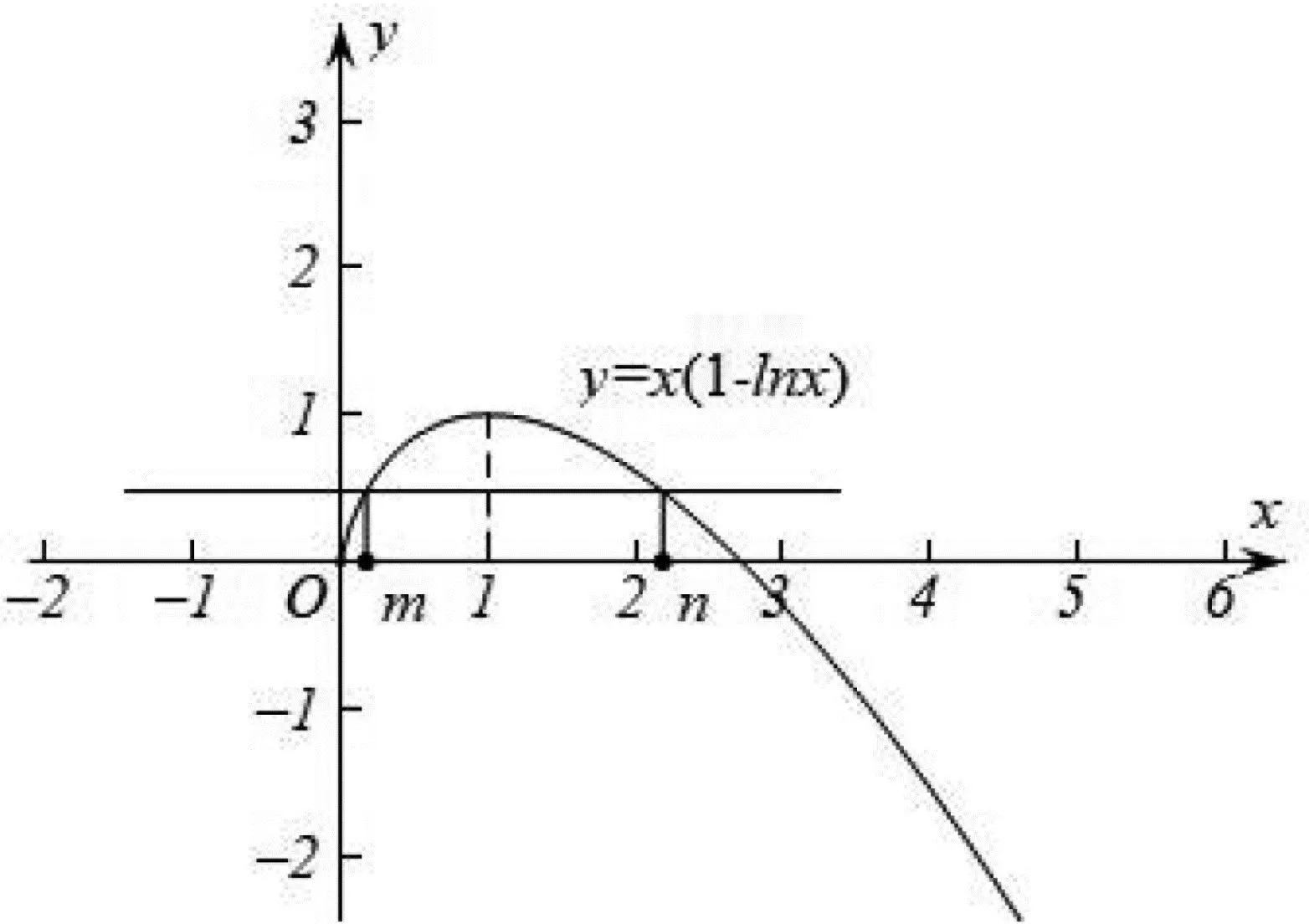
A.eb B.ea C.0 D.0 分析:当x→-∞时,曲线y=ex的切线的斜率k>0且k趋向于0,当x→+∞时,曲线y=ex的切线的斜率k>0且k趋向于+∞.结合图象(图1)可知,两切线的交点R(a,b)应该在x轴上方,且在曲线y=ex的下方,故0 图1 评注:若切点为(x0,ex0),求出切线方程y-ex0=ex0(x-x0),由过点(a,b)得,b-ex0=ex0(a-x0),转化为关于x0的方程b-ex0=ex0(a-x0)有两解进行判断,运算较为繁琐.利用图形直观分析问题,只需判断两条切线的交点(a,b)在x轴上方且在曲线y=ex下方即可解决问题.既体现了借助函数的图形分析和解决问题的优越性,又有助于提高直观想象素养. 例2 设函数f(x)是定义在R 上的单调函数,且∀x∈R,f(f(x)-ex)=e+1.若函数g(x)=f(x)-k(x+2)有两个零点,则k的取值范围是( ). A.(e,+∞) B.(1,e] C.(1,+∞) D.(0,1) 析解:由题意得f(x)-ex为常数,设f(x)-ex=t, f(x)=ex+t,由函数y=f(x)为增函数,及f(t)=et+t=e+1,得t=1,故f(x)=ex+1.函数y=g(x)有两个零点等价于函数y=f(x)与y=k(x+2)的图象有两个不同的交点,画出图象(图2),由图形可直观看出,直线y=k(x+2)与曲线y=f(x)相切时的位置是关键.可求得经过(-2,0)的曲线y=f(x)的切线的斜率k=1.由图象可知,要使y=f(x)与y=k(x+2)的图象有两个不同的交点,k的取值范围为(1,+∞).故选C. 图2 评注:本题求得函数y=f(x)的解析式,把y=g(x)有两个零点转化为函数y=f(x)与y=k(x+2)的图象有两个不同的交点,函数y=f(x)的图象是常见、确定的,而直线y=k(x+2)过定点(-2,0).因此,通过图象分析,确定关键(相切)位置,通过适当计算即可解决问题,从而避免繁琐的数学运算,提高解题效率. 图3 评注:求解(2)问,先通过画图分析,可以确定函数f(x)有且仅有两个零点,及零点所在的大致区域,这是突破分类难点的关键,也是解决本题的关键.明确分类后,进而分区域逐一证明,在证明的过程中还需要在图形的直观引导下进行逻辑推理论证.用图形直观的方法可以更加简单清晰地找到解决思路及预测结果,并引导解题的推理过程. 例4 已知函数f(x)=x(1-lnx). (1)讨论f(x)的单调性; 析解:(1)f(x)的定义域为(0,+∞).f′(x)=-lnx,当x=1时,f′(x)=0;当x∈(0,1)时f′(x)>0;当x∈(1,+∞)时,f′(x)<0.故f(x)在区间(0,1]上为增函数,在区间[1,+∞)上为减函数. 图4 评注:本题(2)小题通过画图,可以直观发现m,n(m 图5 由上述实例分析可见,图形可以为分析和解决函数问题提供重要的直观基础和视觉支撑.在数学解题教学中,常常可以借助图形直观,将复杂问题简单化、抽象问题具体化.利用图形描述分析问题的思维活动,是课堂开展思维活动、培养学生思维品质的重要形式之一.在数学问题解题教学过程中,教师应注重渗透数形结合的思想方法,利用好图形直观的手段与方法,帮助学生直观地寻找解决问题的思路,培养学生识图、画图与析图的能力,提高用图意识,促进解题能力的提升和直观想象的生成.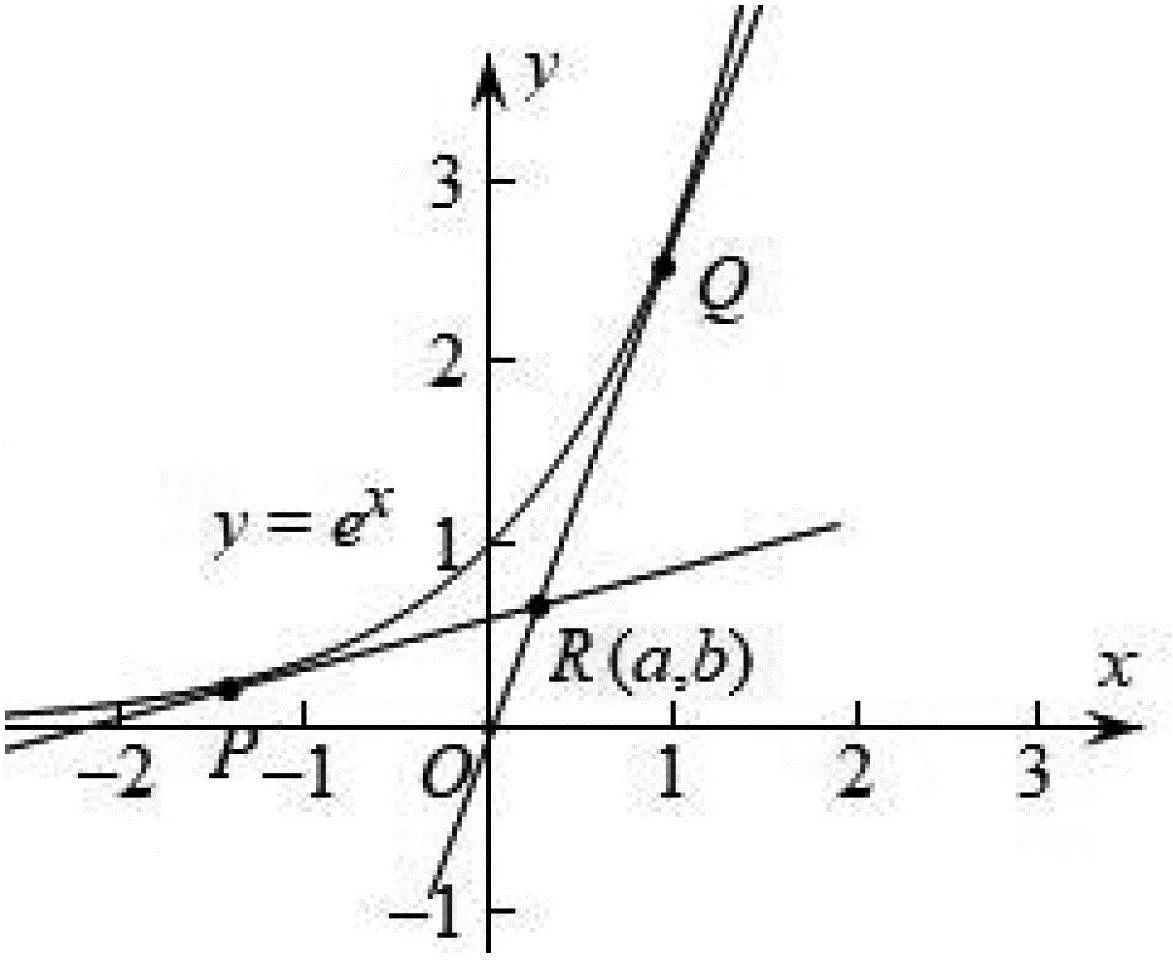
2.运用图形直观,分析和解决函数的零点(方程的根)问题



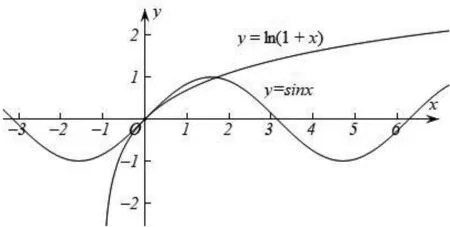
3.运用图形直观,分析和解决函数的偏移问题