作业讲评多“不妨”,生本评价促提升*

福建省南安第一中学 (362300) 洪丽敏

《普通高中数学课程标准(2017年版)》指出“高中数学教学以发展学生数学学科核心素养为导向”,同时指出“教学评价是数学教学活动的重要组成部分,评价应以课程目标、课程内容和学业质量标准为基本依据,日常教学活动评价,要以教学目标的达成为依据.”

数学作业是学生获取数学知识、发展数学思维能力的一项重要的活动形式,同时也是师生之间知识交流互动的一个基本载体.数学老师对课后作业进行恰当的评价,能给学生们带来一种满足感,并能提高他们学习数学的自信心.因此,教师在数学作业批改时,需要通过判断解决问题方法的合理性、创新程度、答案的准确性、写作模式和作业的整洁度等全面评估数学课后作业的质量.当然,在数学作业讲评时,教师要调整传统“你听我讲”的形式,结合作业的反馈情况,多些“不妨……””、合理评价、激励学生.

1 不妨在“纠错辨析”中促“生成”

“对与错”是学生学习效果在作业完成中的直观呈现,“对”固然是好的,但“错”也不失是一面教学诊断的镜子.面对作业中存在的错误,教师不妨珍视错题暴露出来的问题,合理利用,“变废为宝”.

例1 已知函数f(x)是(-∞,+∞)上的偶函数,若对于x≥0,都有f(x+2)=-f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2011)+f(2012)

=( ).

A.1+log23 B.-1+log23 C.-1 D.1

学生的答案只有C或D两种结果,且两种答案几乎是旗鼓相当.为什么?带着疑问,作业讲评时,笔者各自请一代表说出解题思路.

1.1 各显身手

生1:x≥0时,由f(x+2)=-f(x)可知函数f(x)是周期为4的周期函数,又f(x)是偶函数,可推知f(x)是(-∞,+∞)上周期为4的周期函数,所以f(2012)=f(0)=0,f(-2011)=f(1)=1,故选D.

生2:由生1知f(2012)=f(0)=0,f(-2011)=f(-3)=f(3),根据条件f(3)=f(1+2)=-f(1)=-1,故选C.

听了学生1,2的解法后,大部分同学一下子都蒙了,两种解法都那样“无懈可击”.那么问题究竟出错在哪里呢?此时,有相当一部分同学认为题目错了.该如何判决呢?笔者并不急于作出判断,而是把“球”踢给学生.

评注：对于作业中存在的较大面积错误,讲评时,教师不仅要关注正确的解法,更要关注错误的原因(大面积的错误绝非偶然),此时应让“不同声音”得以完整呈现,以便学生在解析之后辨明是非.

1.2 辨明是非

学生通过思考讨论,一部分学生建议画图试试.

若x∈[2,4),则x-2∈[0,2),f(x-2)=log2(x-1)=-f(x),故f(x)=-log2(x-1),故函数f(x)的图象如图1,由图1可知,正确答案为C.

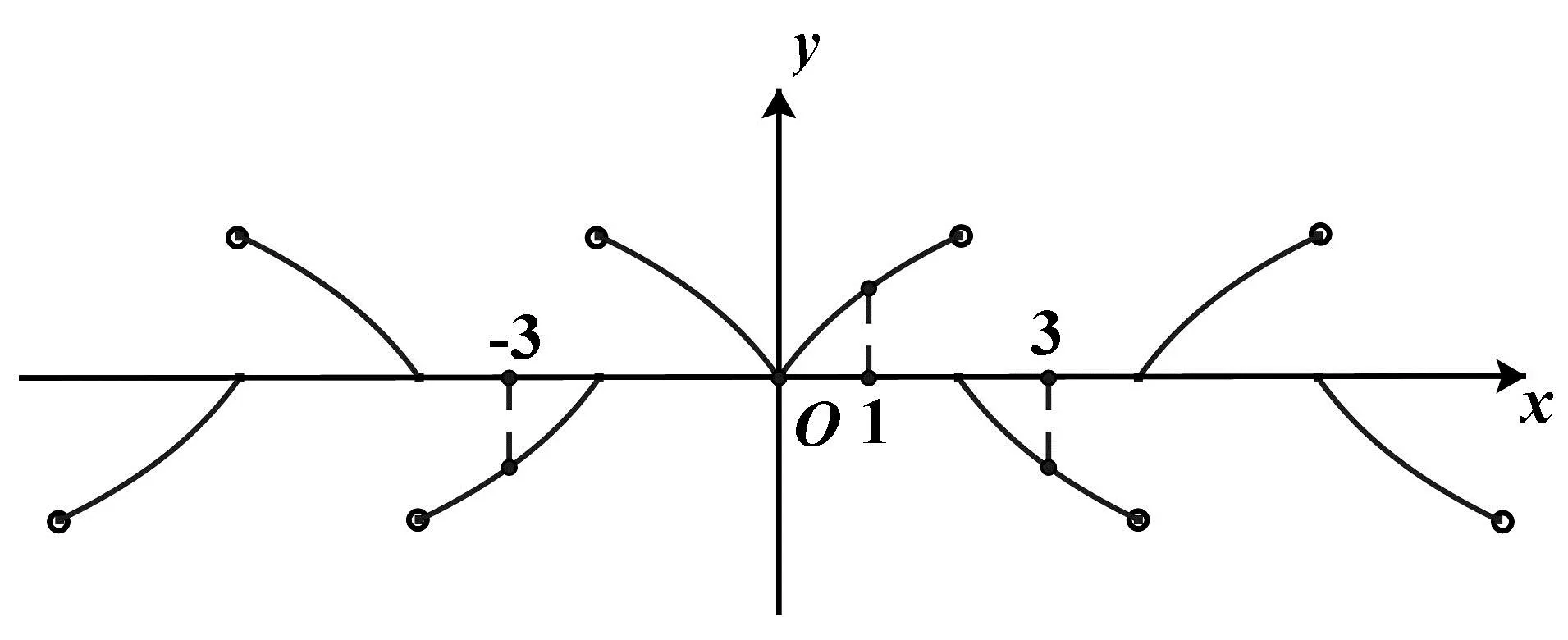
图1

评注：查究错误之源是纠错的重点,此时贵在引导学生领悟“如何找?”,而非“直接给”.本题“纠错”关键在于让学生学会思考――数形结合是解决函数问题的重要方法,既然“数”计算不能辨真伪,那么只能求助于“形”了.

1.3 错因解剖

笔者抓住机会,让学生说说解法1错误的原因.最后形成共识:对于偶函数f(x),f(x)在[0,+∞)上的周期为4,可以推出f(x)在(-∞,0)的周期为4,但f(x)在R上并不是周期函数.(*)

评注：让学生学会对错误的原因进行辨析说理,在说理中有所思、有所得、有所悟.

1.4 因势利导

若函数f(x)是(-∞,+∞)上的奇函数,情况又如何?如图2,我们发现上述结论(*)对奇函数f(x)仍成立.

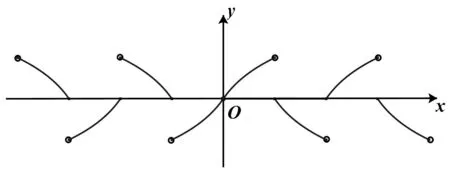
图2

评注：“因势利导、乘胜追击”是纠错后的“强化”环节,一方面可以检测诊断学生对错误的辩证认识,另一方面可以对比、迁移知识.

生本评价:教师对学生作业完成情况的多元评价,将使得作业的强化、反馈效果更上一层楼.“落红不是无情物,化作春泥更护花.”作业中存在的错误,虽没有正确答案那样赏心悦目,但却是教学效果的晴雨表.教师在作业讲评时要善于开发利用错误资源,鼓励学生暴露解题历程,引导学生进行“纠错辨析”,不仅明白“错在哪里?”,更要弄清楚“为什么错?”,最终实现“变废为宝”.

2 不妨在“百花齐放”中促“提炼”

对于同一个题目,不同的学生由于不同的学习体验,常出现不同的解法,形成不同的解题策略.在作业的讲评中,不仅要鼓励学生寻求不同的解法,“百花齐放”,更要善于引导学生注重提炼解题策略.

2.1 作业反馈

方法二:如图3,可知∠CDA+∠ADB=π,则有cos∠CDA=-cos∠ADB.不妨设CD=DB=x(x>0),则BC=2x.在ΔADC与ΔADB及其ΔABC中结合余弦定理可解得b=6.(下同方法一,略)

图3

评注：作业呈现的方法主要是方法一、二(课堂曾解决过三角形中线的问题),学生的作业反馈在笔者的意料之中,笔者欣慰之余又有所期待…

2.2 百花齐放

图4

受生1启发,生2认为可以把三角形补成平行四边形.

图5

图6

评注：对于学生的多样解法,笔者甚感欣慰,尤其方法三,课后笔者曾与该学生交流,“为什么这么想?”,学生说“老师您不是常说‘中点,再找中点,构造中位线’吗?”(有的解题策略的确可以深入人心),让笔者倍感欣慰!

2.3 提炼策略

在欣赏学生的多样解法之余,笔者趁热打铁,引导学生归纳三角形中线问题的常见解题策略:

策略一:利用互补关系(如方法二),此策略可解决一般“爪形结构”情形,属通法;

策略二:构造平行关系(如方法三、四),此策略也可解决非中点情形,属通法;

策略三:利用中点向量形式(如方法一),属最佳解法,也可推广到非中点情形;

策略四:建立坐标系(如方法五),关键在于合理建系,也是解决三角形问题的常见策略.

评注：“提炼策略”是最容易被师生忽视的环节,也常常因为该环节的缺失,学生易陷入“虽有多种想法,但不知如何入手”、缺乏“策略性解决问题”、“只见树木不见森林”的困境.

生本评价:教师对学生作业“百花齐放”解法的及时肯定与赞赏,可以进一步激发学生的学习热情和探究欲望.作业讲评时,教师若能引导学生对多种解法进行反思总结、甄别对比,再加以提炼,辨别通性通法和最佳解法,将使得讲评的效果更佳.

3 不妨在“总结反思”促“提升”

荷兰数学教育家弗莱登塔尔指出:反思是数学思维活动的核心和动力.反思是数学解题过程的最后阶段,也是提高学生解题能力最有意义的阶段.然而,这个阶段常常被忽略.数学作业离不开解题,为此,教师在讲评之余能否引导学生进行解题反思,在某种程度上决定了学生解题的高度.

例3如图7,直三棱柱ABC-A1B1C1中,AB⊥AC,A1A=AB=AC,D是AB的中点.记平面B1C1D∩平面A1C1CA=l,在图中作出l,并说明画法.

图7

在讲评之余,笔者引导学生总结反思两平面交线的作图策略:

一是找两平面的两个交点,则可确定交线(如图8).其作图要点在于:先直观找一个公共点(如点C1);再通过同一平面内的两相交直线确定另一公共点(如本例中的直线B1D和直线AA1相交于点F).

图8

二是构造两平行直线(两平行直线可确定一个平面,如图9),其作图要点在于构造平行关系(常见中位线形式,如本例中C1B1∥ED),需要考生较强的观察能力.

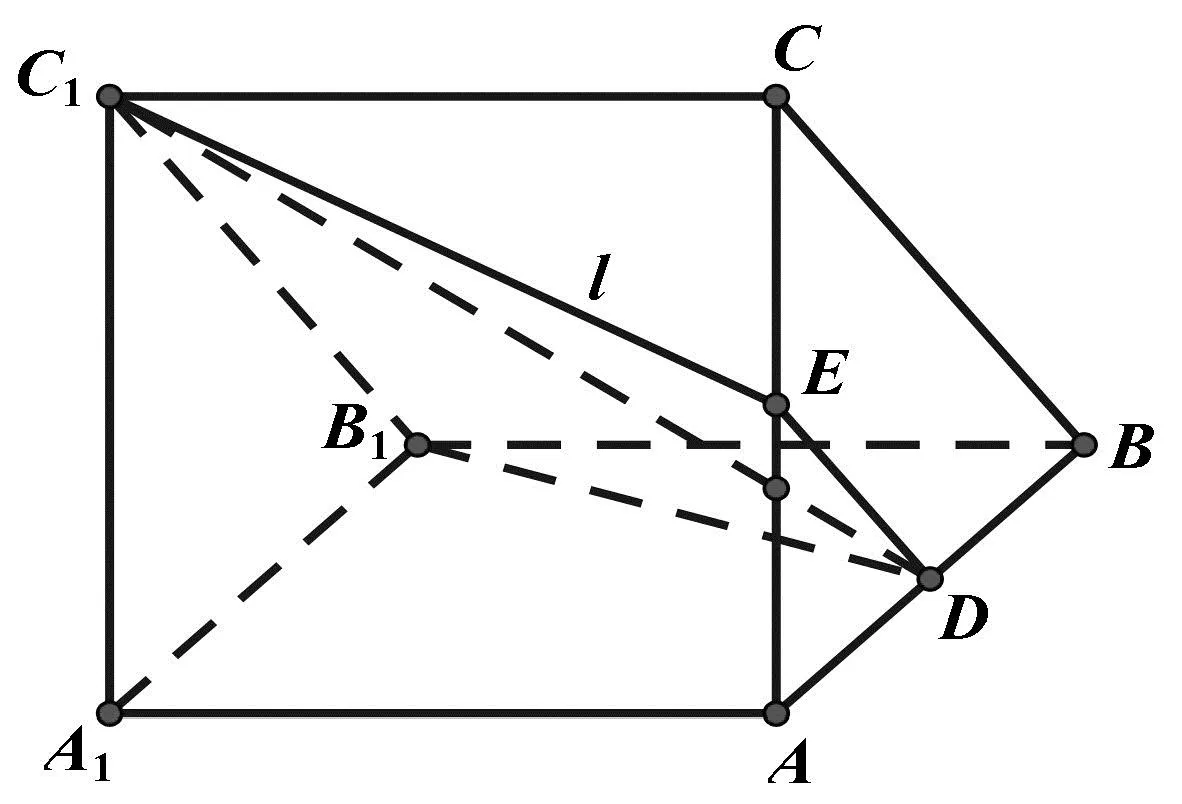
图9

同时要引导学生注意以上两种方法的合理选择.比如图10,四棱锥P-ABCD的底面ABCD为平行四边形,求作平面PAD与平面PBC的交线时,可直接过点P作直线l//AD,则有l//AD//BC,则l为所求直线(此时就不宜用方法一,AD//BC,不相交!)

图10

进而类比思考线面平行的作图策略:比如问题“在平面A1C1CA内过A作一直线m//平面B1C1D”.此时,学生不难把问题化归,如图11,先作出两平面交线l,再作AG与交线l平行.

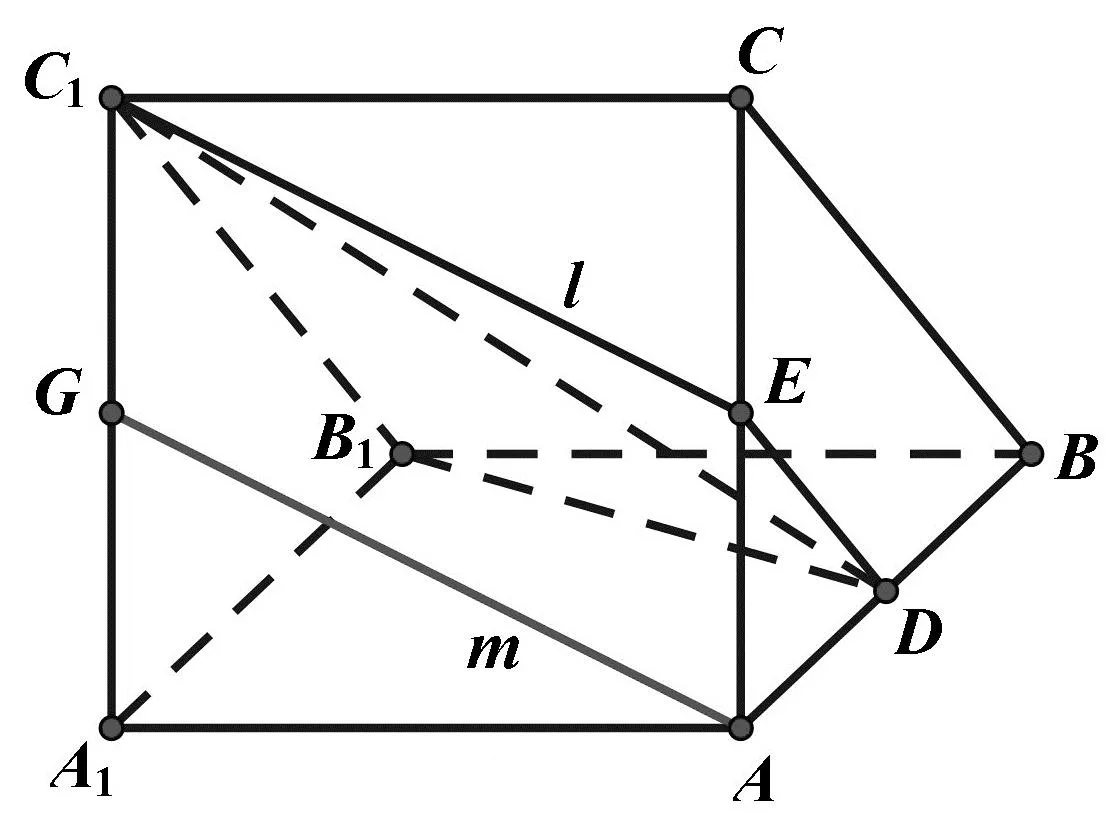
图11

通过这样的反思,学生不再“就题论题”,而是能“由例及类”,其“解题能力”得以在反思中提升.

生本评价:对于“学习解题”而言,学生完成了解题过程,并不意味一次“解题学习”的完成,对解题的真正学习是“回顾解题”.这如同知识获得的保持阶段一样,它是解题学习的“保持阶段”.“工欲善其事,先利其器.”“回顾解题”就是磨利解题武器的过程,可取得举一反三的作用.因此,无论是解题教学还是作业讲评,教师一定要留出时间,让学生回顾解题,在解题反思中提升.

总之,数学作业讲评中,教师不仅要合理评价学生的不同想法,还要学会适当放手,不妨多多创造机会让学生“生成知识”、“提炼策略”,进而“提升能力”,最终实现“教学双赢”.