基于动态点线耦合的单目视觉惯性SLAM算法
2024-03-08黄宜庆张开平
吴 桐,黄宜庆,张开平
(1.安徽工程大学电气工程学院,安徽 芜湖 241000;2.高端装备感知与智能控制教育部重点实验室,安徽 芜湖 241000)
0 引言
近些年来,视觉同步定位与建图(Visual Simultaneous Localization and Mapping,V-SLAM)[1-2]得益于其能够通过可视化的图像提供相当丰富的信息,在无人驾驶、虚拟现实[3]等领域中得到了广泛的应用。为了更好优化V-SLAM算法,研究者们在V-SLAM框架中引入了视觉惯性里程计(Visual-Inertial Odometry,VIO)[4],这是一个将低成本的视觉惯性测量单元(Inertial Measurement Unit,IMU)集成到视觉里程计(Visual Odometry,VO)的系统,通过系统中的视觉传感器(如单目相机)和IMU相互结合,在提取特征信息方面取得了更好的效果[5-6],被广泛应用到实际场景中。
最初的VIO系统是基于点的提取和跟踪来估计运动姿态,例如QIN等[7]提出的VINS-Mono系统是利用OpenCV提供的提取算法对特征点进行光流跟踪及提取,但是基于点的提取有局限性,在重复纹理等复杂的场景中提取的点较少,这很大程度上影响了运动估计姿态的准确性。为了克服这一缺陷,研究者们在基于点提取的基础上,将线特征引入到视觉惯性系统中,PUMAROLA等[8]在ORB-SLAM[9]算法的基础上加入线特征,提出线特征初始化算法。线特征包含的信息比点特征多,应用于缺乏点特征的人造环境中,可以有效提高系统的鲁棒性,基于此特点,研究者们又提出了点线融合的特征提取方法,该方法的优点就是线特征与点特征完全互补,通过相互融合,具有很好的协同作用,有效地提高了系统的准确性与鲁棒性。HE等[10]在VINS-Mono的系统框架上作了修改,提出了一种基于点线特征融合的紧耦合视觉里程计(PL-VIO),该系统使用OpenCV中的LSD(Line Segment Detector)[11]线段提取算法来检测线特征,但是因为它具有高的计算成本,严重影响了PL-VIO系统的性能。刘建军等[12]提出了基于点线特征的快速单目惯性SLAM算法,但是对系统的定位精度提升得不够明显,付煜等[13]用点线融合的方法提取了丰富的线特征,但是提取的线特征质量较差。
针对上述算法存在的问题,本文在VINS-Mono算法的基础上,给出了一种基于点线耦合的单目视觉惯性SLAM算法。通过设定提取线特征的动态阈值,提取新的点线耦合特征并构造点线耦合残差模型,然后将所提出的点线耦合残差集成到后端滑动窗口优化中,并构建优化成本函数对系统进行优化,以提高系统的定位精度和鲁棒性。
1 本文算法结构
1.1 算法框架
本文算法的基本结构与VINS-Mono类似,系统框架结构如图1所示。系统主要包括三个模块,分别是测量预处理、全局滑动窗口优化和闭环检测。在测量预处理模块中,对视觉传感器(相机)采集到的图像进行点线特征检测及跟踪。对于点特征,本文先使用Shi-Tomasi[14]算法检测角点特征,再用KLT(Kanade-Lucas-Tomasi)[15]算法执行点的跟踪;对于线特征,在原来的LSD算法上进行改进,设置动态阈值,用于检测线特征,然后采用几何约束的线特征匹配法对线特征匹配跟踪,最后将提取到的点线特征与IMU预积分视觉惯性对齐。在全局滑动窗口优化模块中,基于滑动窗口的非线性状态估计器可以根据先验信息,IMU残差,闭环约束,点、线残差以及本文构建的点线耦合残差构造联合优函数,计算滑动窗口中的帧的位置、速度、旋转与偏差。对于回环检测模块和原理与ZHAO等[16]提出的PLI-VINS相似,本文就不再叙述。
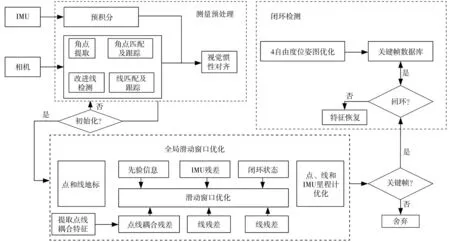
图1 视觉惯性SLAM系统框架结构
1.2 线特征残差模型
线残差模型的建立与点残差类似,将线残差定义为线端点到投影线的距离。本文使用Plucker坐标来描述线段,假设在世界坐标系下的一条空间线Lw=(nw,sw)T,通过转换矩阵Tcw=(Rcw,tcw)将世界坐标系下的空间线Lw转换为相机坐标系下的直线Lc。
(1)
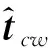
再将相机坐标系下的直线Lc投影到像素坐标平面上,得到投影线[17]L′:
(2)
其中,K为投影矩阵,nc可由式(1)求得。
基于此,可以定义线特征残差[18]el为:
(3)
其中,s为空间线中端点的齐次坐标。
1.3 滑动窗口优化
要进行滑动窗口优化,首先要定义滑动窗口中的状态变量,由VINS-Mono可知,可将完整的状态变量定义为[7]:
(4)
其中,m,n,l分别表示滑动窗口中关键帧、特征点、特征线的数量,xk表示第k个滑动窗口的IMU状态,分别描述了在世界系中IMU的位置、姿态方向、速度、加速度计偏差和陀螺仪偏差。λn表示空间点的逆深度,Ol表示空间线的正交。
然后把边缘化先验残差、IMU测量残差、闭环信息残差、点残差和线残差都加入到后端优化成本函数C中,得到式(5):
(5)
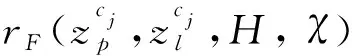
2 点线耦合
2.1 设定线特征提取的动态阈值
传统的线段提取算法存在短线较多和重叠线段不能有效剔除的问题,这些问题会导致视觉传感器对相机位姿的估计不够准确,且难以精确进行全局地图构建。对于点线融合的SLAM系统,线特征是对点特征的补充,只需要保留较长的线特征而剔除较多的短线就可以对相机位姿进行精确估计。本文构造了一种改进的线段提取算法,在线特征提取阶段,设定一个根据具体场景而变化的动态线段提取阈值,这样做的目的是对视觉传感器检测到实际场景的线特征进行保留和剔除,进一步提高相机位姿估计的准确性,从而提升了全局建图的精确度。
定义线段提取的动态阈值为Lmin,则Lmin满足如下公式:
(6)
其中,n表示在第m帧中线特征的提取数量,W与H分别表示当前帧的宽度与高度。
以上公式是根据每帧图像的宽度、高度以及提取到的线特征数量设计而成,避免了传统线特征提取算法由于设置固定阈值的原因致使提取有效的线特征较少或提取多余短线段的结果,从而对线特征有合理且有效的利用。
再将提取到的所有线特征定义为一个集合{l1,l2,…,ln},则线段长度筛选机制遵循以下公式:
Lli≥Lmin,i⊆{1,2,…,n},
(7)
其中,Lli表示提取到线段的长度,当Lli大于或等于阈值Lmin时,线段被保留下来,反之线段会被剔除。
2.2 提取点线耦合特征
LSD算法是检测线特征的常用方法之一。由于该算法计算灰度图像中每个像素的水平线角度并分割具有相似水平线角度的连接区域,可以在线特征的端点处检测角点特征。因此在线段的末端检测到的角点特征与线特征存在位置关系,这种位置关系被定义为点线耦合特征。
在本文中,将特征点与距其最近的特征线进行耦合,然后提取融合后的特征,具体的做法如下:使用K-D树(K-Dimensional Tree)快速搜索算法,在以特征点为圆心、半径为r的圆中搜索线特征的端点,将距离圆心最近的线特征端点所在的特征线视为距离特征点最近的特征线,并将其与特征点融合并提取(图2)。
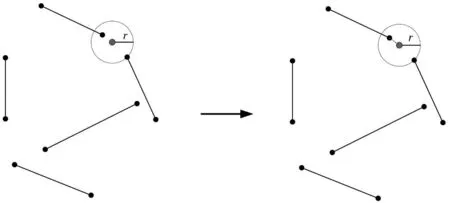
图2 点特征搜索线特征示意图
如果点线特征成功耦合后,可以得到一个关于点特征、线特征和帧三者之间的关系式:
H={h|h={p,l,ci,cj}},
(8)
其中,p表示点特征,l表示线特征,ci与cj表示不同的两帧,h为点线耦合特征的描述符,H表示h的集合。
2.3 点线耦合残差模型
在全局优化中,本文采用BA(Bundle Adjustment)算法估计点特征的深度,点特征的深度估计的准确性和稳定性受跟踪帧数的影响。跟踪帧数越多,深度估计就越准确、越稳定,相反,若跟踪帧数少,就可能导致不稳定。在本文中,在滑动窗口内设置一个点跟踪帧数的阈值μ,若点跟踪的帧数小于μ,就在滑动窗口优化中引入本文构造的点线耦合残差,利用所提出的点线耦合残差进行鲁棒定位。点线耦合残差模型如图3所示。
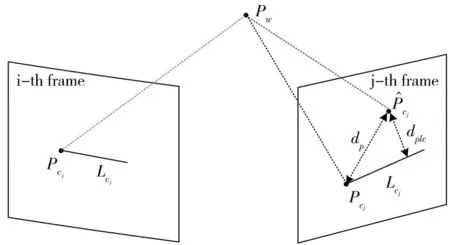
图3 点线耦合残差模型
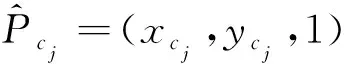
ax+by+c=0.
(9)
若已知直线的起点Lcjs=(xcjs,ycjs)和终点Lcje=(xcje,ycje),则可以计算出式(9)所表述直线的常系数,如式(10)所示。
(10)
将直线的常系数集合定义为M(Lcj),称之为直线的性质,如式(11)所示。
M(Lcj)=[a,b,c].
(11)
(12)
3 实验与分析
本文算法的实验平台是一台处理器为Intel®CoreTMi3-8100,运行内存是8 GB,操作系统为Ubuntu 18.04 LTS 64位的计算机。
将本文算法在EuRoC数据集的MH_04_difficult序列进行了仿真实验,得到了点线融合特征图像和算法运行的轨迹,如图4所示。图4(a)中的线条表示线特征,小圆点表示点特征,从图4(a)可以看出,在黑暗环境下,点特征稀疏,但本文算法提取到了丰富的线特征,且在线特征提取时,剔除了多而短小的线段,保留了比较长的线段。在图4(b)中,颜色深的线表示本文算法的运行轨迹,颜色浅的线表示真实轨迹,可以看出本文算法的运行轨迹与真实轨迹一致。

(a)点线耦合图 (b)运行轨迹 图4 本文算法在MH_04_difficult序列的仿真图
进一步,在MH_04_difficult、V1_03_difficult和V2_03_difficult三个难度大的序列中,将本文算法与VINS-Mono算法、PL-VIO算法进行对比,得到各自的三维绝对轨迹误差,实验结果如图5至图7所示。图中的虚线与实线分别表示真实轨迹和估计轨迹,竖直条状带表示误差等级,颜色越深误差越小,颜色越浅误差越大。从图中可以看出,本文算法的估计轨迹颜色深的居多,表明本文算法相对于VINS-Mono算法与PL-VIO算法的定位误差更小,从而具有更高的定位精度。
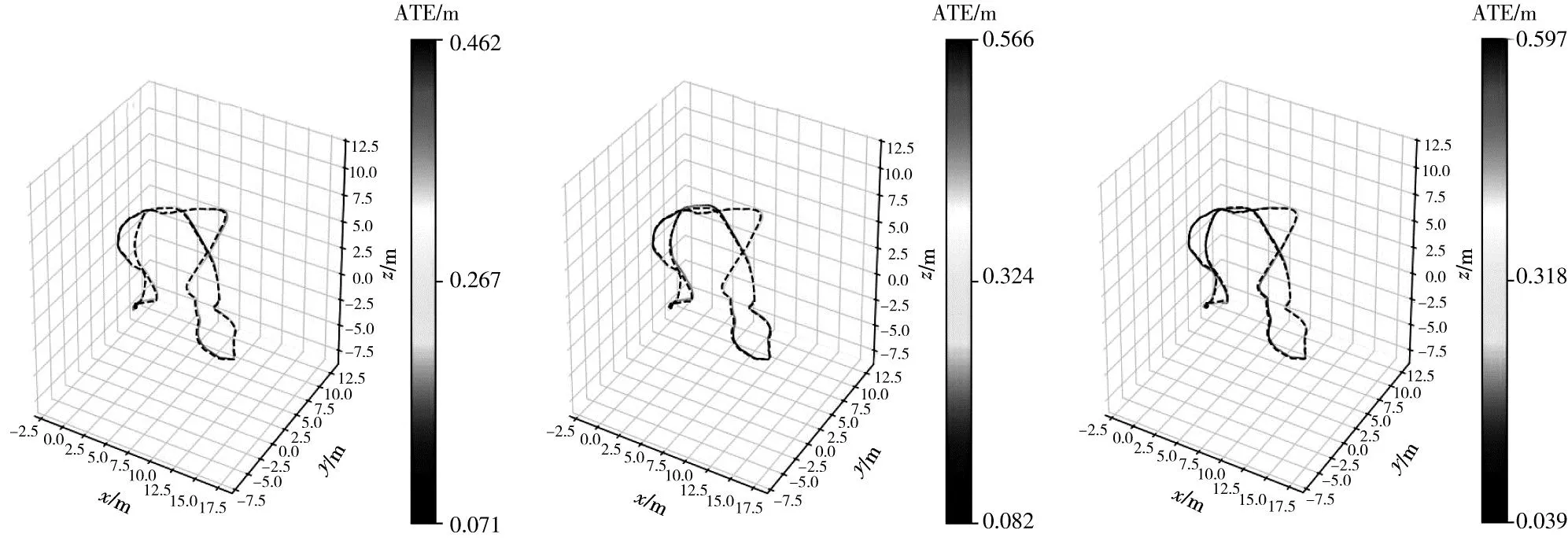
(a)VINS-Mono (b)PL-VIO (c)本文算法 图5 三种算法在MH_04序列的三维绝对轨迹误差图
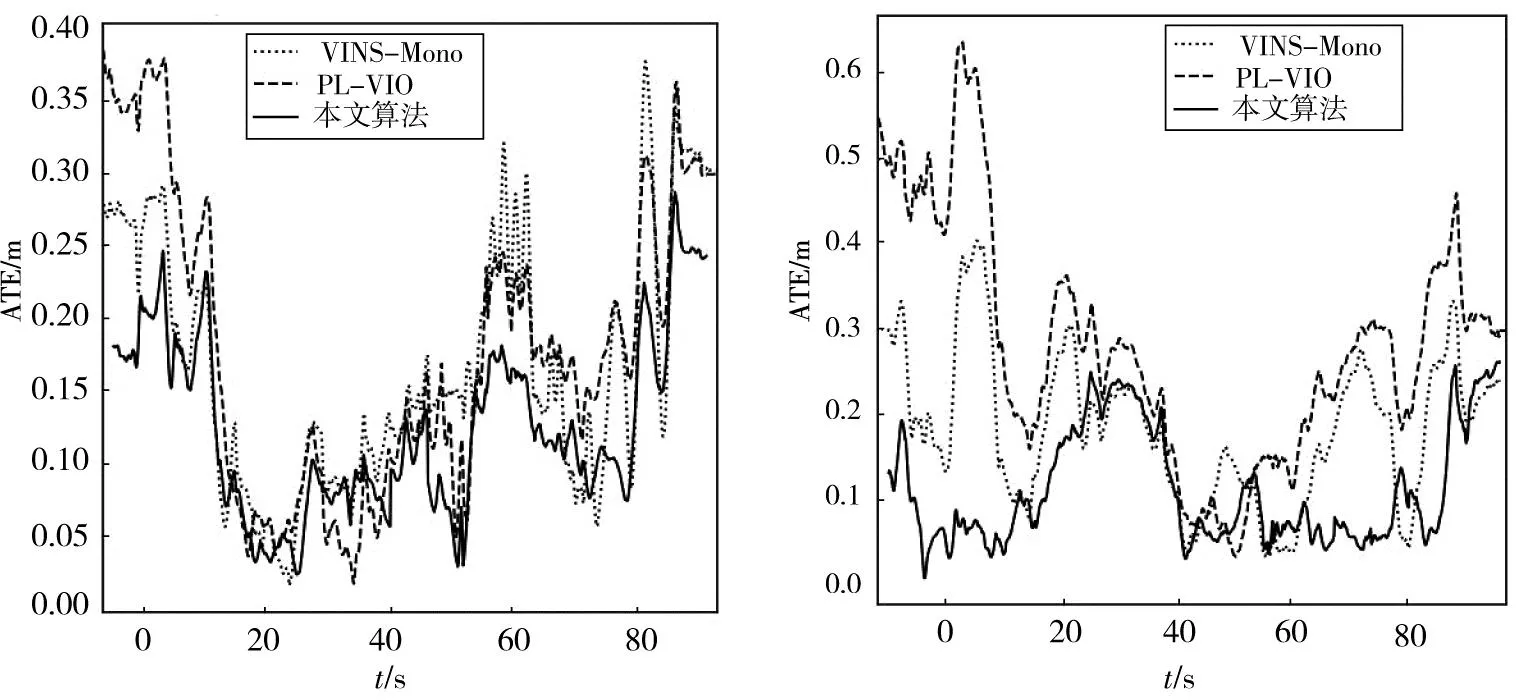
图8是VINS-Mono算法、PL-VIO算法和本文算法在两个序列中的实时绝对轨迹误差曲线图。
(a)V1_03序列 (b)V2_03序列图8 三种算法在两序列的实时绝对轨迹误差曲线图
从图8可以直观地看出,本文算法的轨迹误差曲线整体上是低于另外两种算法,且误差的峰值比另外两种算法小,表明本文算法与VINS-Mono算法、PL-VIO算法相比,取得了更小的定位误差,再次验证了本文算法要优于另两种算法。
图9和图10表示VINS-Mono算法、PL-VIO算法和本文算法在V1_03和V2_03序列中绝对位姿误差的分布情况。从图9可以看出,VINS-Mono算法、PL-VIO算法和本文算法在V1_03序列的绝对位姿误差分布分别为0.05~0.40 m、0.05~0.40 m、0.05~0.30 m,从图10可知,三种算法在V2_03序列的对位姿误差分布依次为0.05~0.40 m、0.05~0.40 m、0.05~0.30 m。由此可知,本文算法的绝对位姿误差的分布区间均比VINS-Mono算法和PL-VIO算法小,进而可得,本文算法的绝对位姿误差分布范围更集中,说明采用本文算法的系统鲁棒性更强,使系统的稳定性更好。
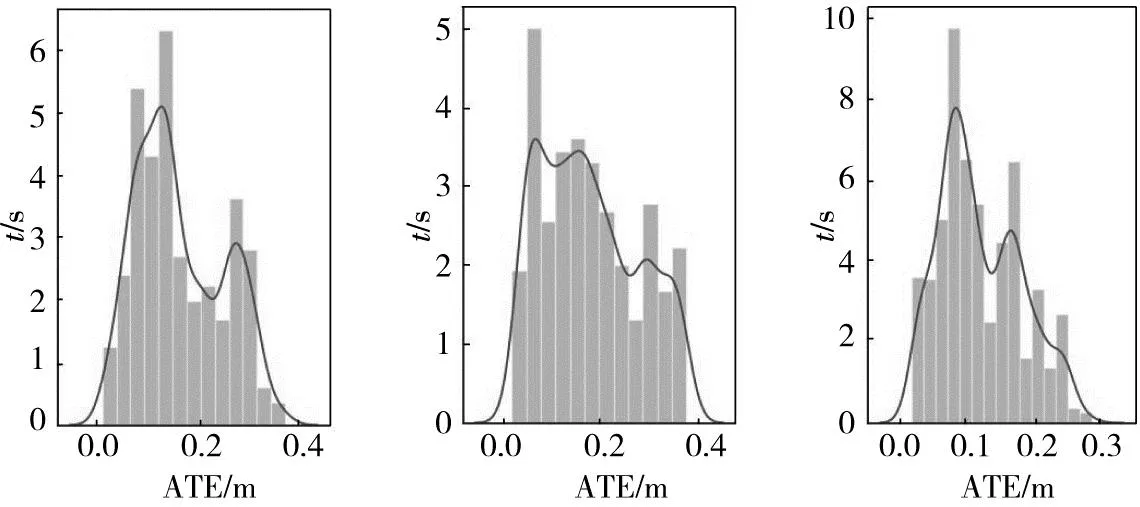
(a)VINS-Mono (b)PL-VIO (c)本文算法 图9 三种算法在V1_03序列绝对位姿误差分布
为了在数值上更好地说明本文算法的优点,将本文算法在11个EuRoC公共数据集上进行多次仿真实验取平均值,并与之前的VINS-Mono算法、PL-VIO算法的结果作对比。在EuRoC数据集下的不同算法的绝对轨迹的均方根误差(RMSE)和标准差(STD)如表1所示。
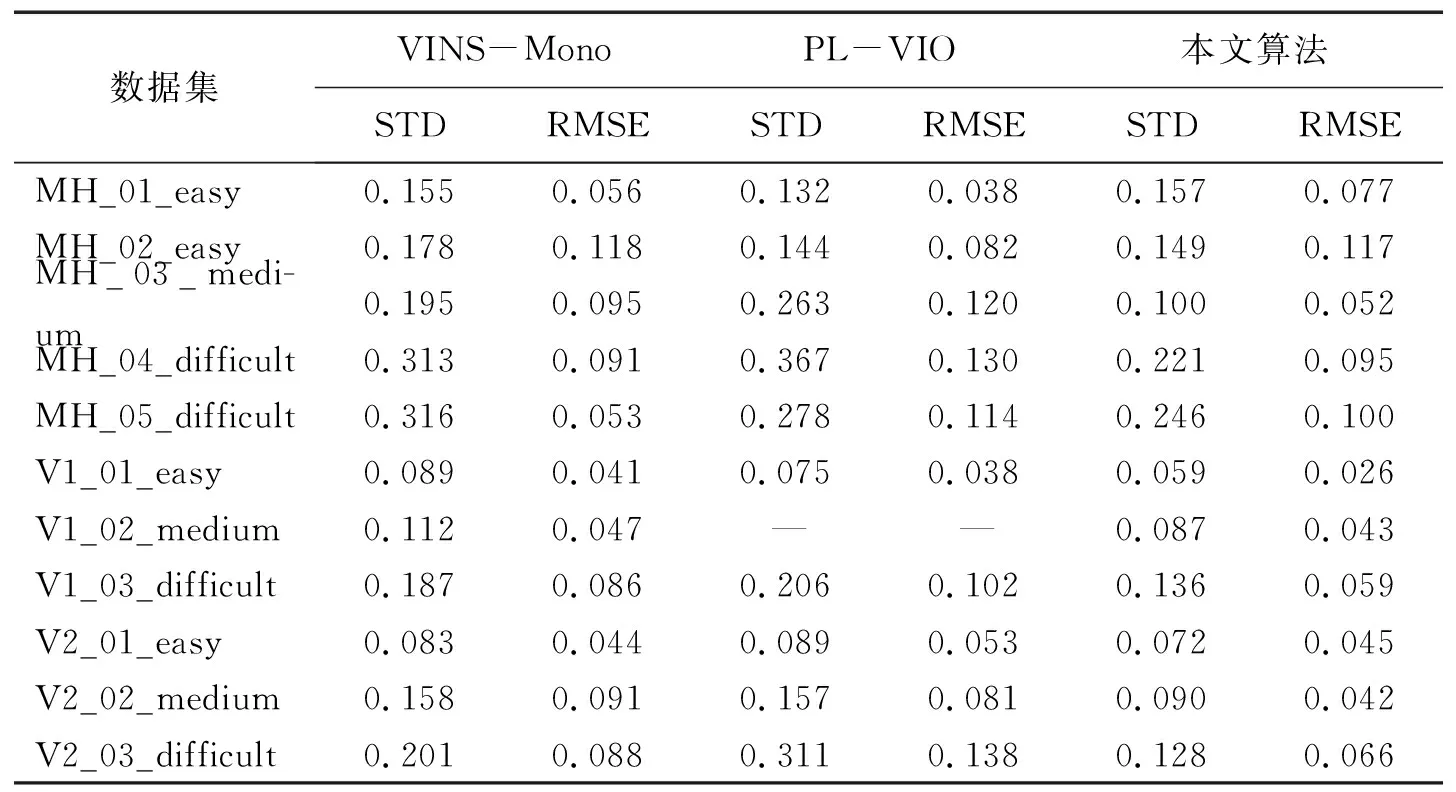
表1 不同算法的位姿估计误差
从表1数据可以直观地看出,本文算法相较于VINS-Mono和PL-VIO算法,绝对轨迹误差在大多数序列中有明显降低,这表明算法的定位准确度有了明显提升。本文算法在MH_03_medium序列中的轨迹精度比VINS-Mono算法提升了48.7%,在V2_03_difficult序列中的轨迹精度比PL-VIO提升了58.8%。
4 结语
本文构造了一种动态点线融合的单目视觉惯性SLAM算法。在传统点特征视觉SLAM算法基础上加入了改进后的线特征提取算法,在线段处理阶段,通过设置提取线特征的动态阈值,处理冗余的线段,实现对线特征的有效利用,提取新的点线耦合特征并构造点线耦合残差模型,用以构造最小化成本函数。通过在EuRoC数据集上的仿真实验表明,本文算法相较于VINS-Mono算法和PL-VIO算法,得到的位姿估计误差均有明显降低,所得到的估计轨迹更接近于真实的轨迹,表明本文所构造的算法提升了系统的定位精度,使系统更具有鲁棒性。
