基于改进突变级数法的引水隧洞施工安全综合评价

张 贺，聂元东

（上海勘测设计研究院有限公司，上海 200335）

引水隧洞是水利工程的重要组成部分， 大型引水工程建设需要穿越山体，且多为隧洞形式［1］。相较于地上空间，其施工环境存在地质和施工条件恶劣，高危作业风险众多，危险源交叉频繁等问题，导致不安全事故时有发生［2］。识别并防范引水隧洞施工潜在危险源，提升企业风险管理能力，能够有效减少事故发生几率，减少企业损失。因此，应针对引水隧洞施工环境特点，对引水隧洞施工安全进行系统分析和风险评估，以期提升水利施工企业安全管理效率。

近年来， 国内外众多学者针对水利施工安全风险分析和风险评估方法进行深入研究。 钟登华等［3］运用改进集对分析方法对高心墙堆石坝填筑工期过程进行了仿真和风险评价， 建立了多元联系数表达的施工进度网络计划模型， 并针对性地提出了基于改进集对分析方法的风险评价蒙特卡洛仿真流程。郑霞忠等［4］基于D-S 证据理论的方法，对引水隧洞作业人员安全行为水平进行分析， 提出了基于D-S证据理论的作业人员安全行为评价方法。然而，缺乏系统化的评价体系以评估水利工程全过程风险状态。陈述等［5］基于系统理论的视角，充分分析水利工程施工安全标准化所具备的特点， 系统提出了水利工程施工安全标准化体系。

以上研究对引水隧洞施工提供了理论参考，然而这些研究多基于静态视角对水利工程进行风险评估，忽略了施工过程的动态风险和风险相关性。此外水利工程和引水隧洞工程施工内容存在一定差异，仍缺乏针对引水隧洞施工风险评估的相关研究。相比静态风险理论评估过程， 突变理论关注风险动态过程，能够有效弥补前者在施工风险分析中的不足。鉴于此，本文基于突变理论视角，提出了引水隧洞施工安全评价方法， 以期为水利工程施工风险分析和管理提供新颖的分析模型和理论工具。

1 引水隧洞施工安全评价指标

1.1 引水隧洞施工安全突变特征

突变理论首先由法国数学家Rene Thom 在1974年提出，以拓扑学和奇点理论为工具，研究系统在动态发展过程中的非连续变化和突变现象［6］。在应用突变理论对系统进行分析时， 首先要确定系统在动态的过程中会出现突变， 即受到扰动后系统的稳定状态会突然转化为另一种稳定状态。 引水隧洞施工存在多种风险因素，多种风险因素之间相互影响。因此，在进行引水隧洞的安全评价时，应厘清风险因素之间的相互影响关系，以建立可靠的评价指标体系。本文基于水利工程的引水隧洞施工背景， 对其安全事故的演化过程进行分析， 归类总结引水隧洞发生安全事故特征，如表1。

表1 引水隧洞工程施工安全突变特征分析

1.2 引水隧洞施工安全评价指标体系构建

由于引水隧洞施工存在多种风险因素， 且多种风险因素之间相互影响。 因此在进行引水隧洞的安全评价时厘清风险因素之间的相互影响关系， 对建立完善的评价体系至关重要。 在筛选引水隧洞突发事故的影响因素时，要坚持科学性、综合性、系统性和可比性等原则。根据之前的研究，收集了水利工程中引水隧洞安全管理的大量资料［7］，结合以上引水隧洞施工安全突变特征分类和引水隧洞施工现场情况， 共厘清14 个引水隧洞施工安全状态影响因素，具体的指标体系及突变类型如图1。

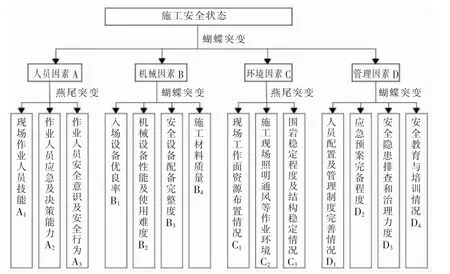
图1 水利工程引水隧洞安全状态影响因素指标体系

2 模型构建

2.1 ISM-ANP 组合赋权方法

水利工程引水隧洞施工情况复杂，安全风险因素众多， 不同风险因素之间相互联系。ISM 模型能够分析引水隧洞安全状态影响因素之间的相互关系，展示各影响因素之间的关联［8］。网络层次分析法（ANP）是层次分析法（AHP）的扩展，适用于系统中元素之间、 元素集之间存在相互影响的网络结构决策问题。 鉴于此， 本文构建ISM-ANP 组合赋权方法，组合赋权模型的步骤如下：

第一步：建立邻接矩阵。将图1 的14 个安全状态影响因素记为Xi（i=1,2,...,14）建立14 阶矩阵，若Xi与Xj之间存在相互影响的关系则在14 阶矩阵中记Xij=1,若不存在相互影响的关系则记Xij=0。

第二步： 计算可达矩阵并建立ISM 层次结构模型， 设矩阵Y 为矩阵X 和其单位矩阵I 的和，当Y1≠Y2≠...Yr-1≠Yr时，则可达矩阵R=Yr-1。根据可达矩阵R 可求得可达集合R（Xi）的前因集合Y（Xi）。其中，R（Xi）为可达矩阵R 各行元素为“1”时所对应的各行的要素组成的集合，Xi表示能够影响到的所有因素。Y（Xi）可达矩阵R 各行元素为“1”时所对应列的要素组成的集合， 表示所有Xi能产生的所有因素。 对影响地下施工安全状态的因素进行层级分类时需满足如下原则：R（Xi）∩Y（Xi）=R（Xi）。

第三步：构造控制层次和网络层次。首先界定决策目标，本文中决策目标为引水隧洞施工安全状态。其次归类安全状态影响元素集， 基于ISM 模型分析结果，分析元素集之间的相互关系及其内部关系，即分析一级指标之间的相互关系及一级指标下内部安全状态影响因素之间的相互关系。

第四步：构造ANP 超矩阵计算安全影响因素权重。首先需在专家意见下使用间接度优势比较法，对14 个引水隧洞施工安全影响因素进行两两比较，运用1～9 标度构造各引水隧洞施工安全状态影响因素的两两比较判断矩阵, 将判断结果输入超级决策软件（Super Decision）中对判断矩阵进行归一化处理和一致性检验，最后得到初始超矩阵。然后根据未加权超矩阵—加权超矩阵—极限超矩阵的顺序得到影响因素的权重。

2.2 突变模型构建

在突变理论中将势函数f(x)作为系统的状态变量，x 作为系统中的控制变量。在实际应用中，首先建立势函数将其作为确定系统状态突变临界点的依据，所有的临界点集合为一个平衡曲面。对建立的势函数f(x)进行一阶求导得到f(x)'，令f(x)'=0 得到平衡曲面的方程，再对f(x)进行二阶求导得到f(x)''，令f(x)''=0 得到平衡曲面的奇点集合。将上述两个等式联立和整合就可以得到分解形式的分歧方程，从而得到归一化公式。在突变系统中当控制变量小于5个时，有7 种基础突变模型；当状态变量只有1 个时，有4 种基础突变模型，分别为折叠型、尖点型、燕尾型和蝴蝶型。 其势函数公式和归一公式如表2。

表2 基础突变模型及其归一公式

突变级数法避开了人为给指标赋权， 一定程度上减少了评价结果的主观性， 但是突变级数法中仍然需要对指标进行重要性排序。 除此之外由于归一公式的聚集特点会使得最后的隶属值偏高并趋于1。因此为了得到更为准确的评价结果，本研究对传统的突变级数法进行以下两个方面的补充和修正，对指标进行权重排序时使用ISM-ANP 组合方法，以期得到较为客观的权重排序。

2.3 改进的突变级数安全状态评价

采用突变级数法对引水隧洞施工安全状态进行评价时，首先要明确发生的突变类型。根据图1 和表1 可知道影响引水隧洞施工安全状态的共有人、机、环、管4 个因素，属于蝴蝶突变；在人员因素这一维度中又有3 个二级影响因素，属于燕尾突变；在机械因素这一维度中有4 个二级影响因素， 属于蝴蝶突变；在环境因素这一维度中有3 个二级影响因素，属于燕尾突变； 在管理因素这一维度中有4 个二级影响因素，属于蝴蝶突变。

记录每项指标的均值、最大值与最小值，以此为基础，然后对评价指标进行标准化处理。根据“互补”和“不互补原则”得到突变级数。采用公式（1）进行标准化处理，z 为指标安全程度分值。

在引水隧洞施工安全状态等级评价中， 本文采用0-1 等级隶属评价方法， 引水隧洞施工安全状态等级分级标准如表3。 当二级指标突变级数隶属值为0.1 时，每一项影响因素的安全等级是极差的，那么引水隧洞施工安全等级也应为极低。 同样当每一个二级指标的突变级数隶属值为0.9 时，每一项影响因素的安全等级都极高，则总体引水隧洞施工安全等级也为极高。

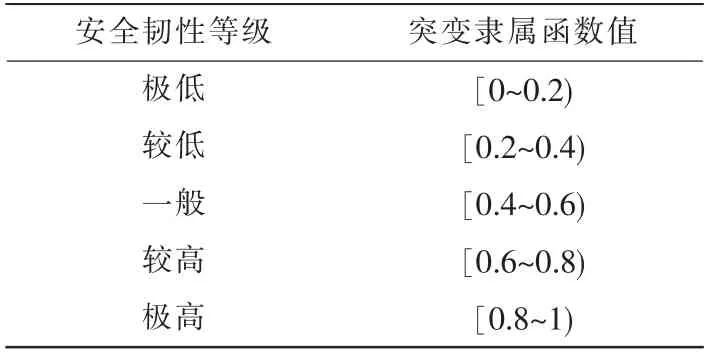
表3 引水隧洞施工安全状态等级分级标准

3 引水隧洞施工安全状态评价

3.1 基于ISM-ANP 方法确定指标权重

为提升评价指标赋权有效性， 本次研究以某引水隧洞工程为研究基础， 采用定性和定量相结合的评价指标方法，评估指标划分依据如表4。本文对模糊性的评价指标和运营指标设置了1-5 级整数区间级别进行赋值，分别对应1-5 的权重分数。

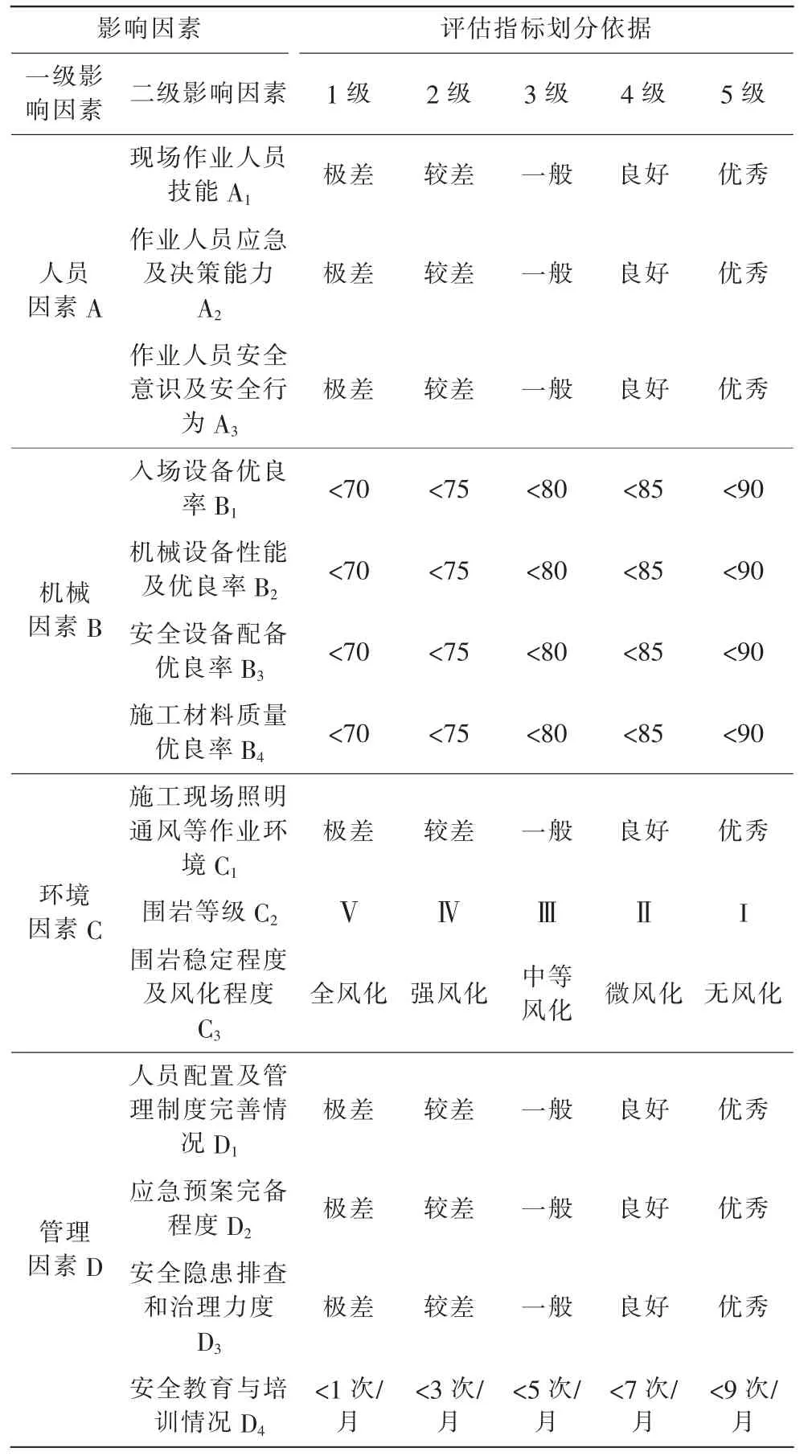
表4 引水隧洞施工安全评价影响因素指标划分依据

数据获取分为专家调研和引水隧洞工程运行数据归一化分析。其中，专家调研数据由23 位分别来自项目技术人员、科研人员、设计人员和勘察人员等具有多年工作经验的专家填写获得； 引水隧洞工程运行数据选取近3 个月的相关运营管理数据平均值运行数据。经过归一化处理后，基于ISM 结构模型分析方法， 引水隧洞施工安全状态影响因素的ISM 结构模型如图2。

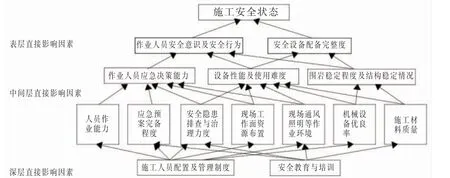
图2 ISM 模型引水隧洞安全状态影响因素层级图

一般元素集内部不存在相互独立， 是既有依存又有循环的网络层次结构。 由上一步得到的ISM 模型可构建出引水隧洞施工安全状态的ANP网络结构如图3。

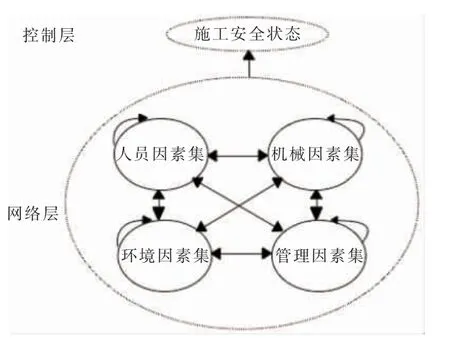
图3 ANP 网络结构示意图

然后根据未加权超矩阵—加权超矩阵—极限超矩阵的顺序得到最后引水隧洞施工安全状态影响因素的权重， 使用超级决策软件后得到的水利工程引水隧洞施工安全状态影响因素的权重如表5。

表5 引水隧洞施工安全状态影响因素权重

由表4 可知， 引水隧洞施工安全状态二级影响因素在人、机、环、管4 个维度中重要性排序分别为{A3,A2,A1}，{B3,B1,B2,B4}，{C3,C1,C2}，{D1,D2,D4,D3}。 每个维度的权重为其二级影响因素权重指标之和， 分别为：A=0.2832，B=0.1881，C=0.1949，D=0.3338，各维度相对重要性排序为{D,A,C,B}。

3.2 突变级数分析

使用互补原则， 采用xA1～xA3的均值作为人员因素的评价指标值。通过上述步骤计算得到xB1～xB4，xC1～xC3，xD1～xD4，结果如表6。

表6 指标归一化结果

在评价水利工程引水隧洞的安全状态时，有A、B、C、D 4 个影响因素，突变类型为蝴蝶突变，且重要性排序为{D,A,C,B}。所以通过归一化运算后得到：

使用互补原则后得到最后引水隧洞施工安全状态的突变级数值为x=0.9199， 根据表2 中的安全等级隶属表可知，某引水隧洞施工安全等级为安全。但由于在突变级数的计算中，归一化会使得最后评价结果过高且趋于1， 因此需要对突变级数值进行修正，使评价等级更为清晰和准确。同理得到二级指标突变隶属值为0.2～1 时引水隧洞施工安全状态突变隶属值如表7。

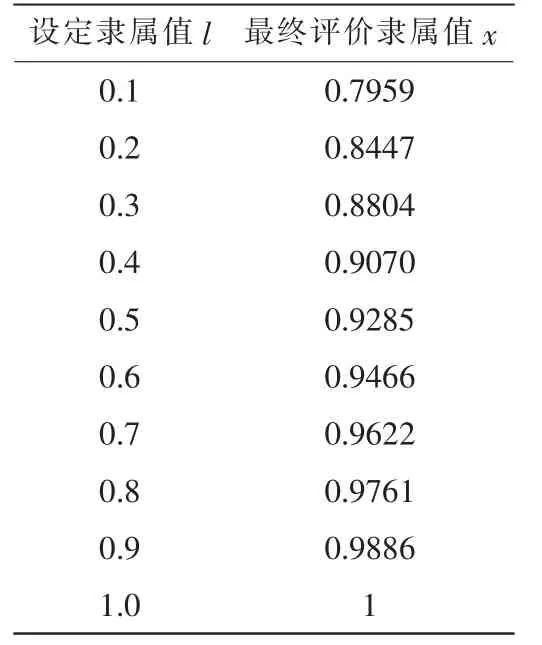
表7 设定二级指标隶属值与最终评价隶属值对照

将设定二级指标的隶属值l 与最终评价的隶属值x 进行拟合，拟合后的公式为l=1.0277·x9.9299，拟合结果如图4。突变级数值为x=0.9199 带入可得最终优化后的引水隧洞施工安全状态突变隶属值为0.4486。与表2 可知，该引水隧洞施工安全评价等级为一般， 表明该引水隧洞施工中存在一定安全隐患。进一步通过ISM-ANP方法，对影响引水隧洞施工的14 个安全因素进行权重分析，可知人员配置及管理制度完善情况、作业人员安全意识及安全行为、作业人员应急及决策能力、应急预案完备程度和现场作业人员技能是占比较重的安全影响因素。 其次重要的是安全教育与培训情况、围岩稳定程度及风化程度、安全隐患排查和治理力度、围岩等级和施工现场照明通风等作业环境。

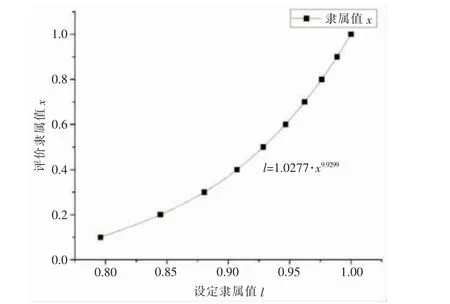
图4 二级指标隶属值l 与x 拟合曲线

4 结语

（1）提出改进的突变级数引水隧洞施工评价方法，并引用ISM-ANP 组合赋权，能够有效降低传统安全评价主观性影响，更准确地反应了评价结果。

（2）该引水隧洞施工安全评价等级为一般，引水隧洞施工中存在一定安全隐患， 评估结果与实际工程情况相符，验证了模型的有效性。

（3）研究结果为系统评价引水隧洞施工安全、降低引水隧洞施工发生安全事故的可能性提供了理论参考。