考虑状态受限和一致性的微电网二次控制
2024-03-07吴忠强程洪强
吴忠强,程洪强
(燕山大学工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)
1 引言
微电网是目前二次能源开发与利用的一个趋势,它由分布式电源、储能元件、控制模块、负载等组成[1].分布式电源(distributed generations,DG)可由风力发电或者光伏发电等新能源提供.这些新能源可重复利用,能源利用效率高,安全可靠,并能减少环境污染以及能源不足等问题[2].传统微电网通常采用下垂控制实现功率的分配,控制方式简单,然而下垂控制是有差调节[3],对此,许多研究者开始采用集中控制和分散控制解决下垂控制产生的偏差问题.文献[4]采用集中控制,利用事件触发机制设计控制器对电压和频率进行控制,但是,集中控制对单点故障的处理能力较弱,进而影响系统的动态性能.文献[5–6]基于分散控制设计了频率恢复控制器,采用无互联线方式,对网络通信的依赖性弱,但是整体的协调性也弱.
鉴于集中和分散控制存在的问题,分布式控制越来越被重视[7–8].文献[9–10]利用小信号动态模型,提出一种基于分布式控制的频率和电压恢复策略,实现了精确的无功功率分配.文献[11–12]研究了分布式有限时间二次电压和频率控制,系统在有限时间内收敛且具有更好的抗干扰性能.
在微电网中,电压和频率这些实际物理状态通常不可避免地受到一定程度的约束,如母线电压变化一般不宜超过10%,频率变化不宜超过2%,否则会对系统的稳定运行造成严重影响.文献[13]研究了电压和频率受限的交流微电网二次控制问题,采用模型预测控制方法,解决状态约束问题.文献[14]采用分布式鲁棒控制方法确保孤岛微电网的频率约束,维持孤岛微电网的弹性运行.
本文针对交流微电网一次控制中产生的电压和频率偏差问题,设计了一种考虑状态(电压和频率)受限的自适应模糊二次电压和频率控制器,以解决交流微电网中的物理状态约束问题.本文的贡献如下:
1)在电压和频率控制器的设计过程中,引入自适应模糊系统对未知变量以及未知扰动进行估计,以提高控制精度和系统的鲁棒性.
2)考虑电压受限问题,基于多智能体系统的一致性协议,利用Backstepping法结合障碍Lyapunov函数(barrier Lyapunov function,BLF)法设计电压控制器以约束电压误差,使输出电压约束在预设的范围内.
3)给出了严格的稳定性证明.
2 预备知识
2.1 图论
多智能体分布式一致性协调控制可以用有向图表示.设有向图G(V,E),其中顶点集V={v1,v2,···,vn},边集E ⊂V ×V.矩阵A=[aij]∈RN×N为图G的邻接矩阵,其中aij表示顶点vi与顶点vj之间的权重.当且仅当(vj,vi)∈E时,意味着顶点j能接收到来自顶点i的信息[15],否则aij=0.定义对角阵D与图拉普拉斯矩阵L分别为:D=diag{d1,···,dN}∈,L=D-A ∈RN×N,对于有向图来说,L的第i行的元素之和等于0.
2.2 引理
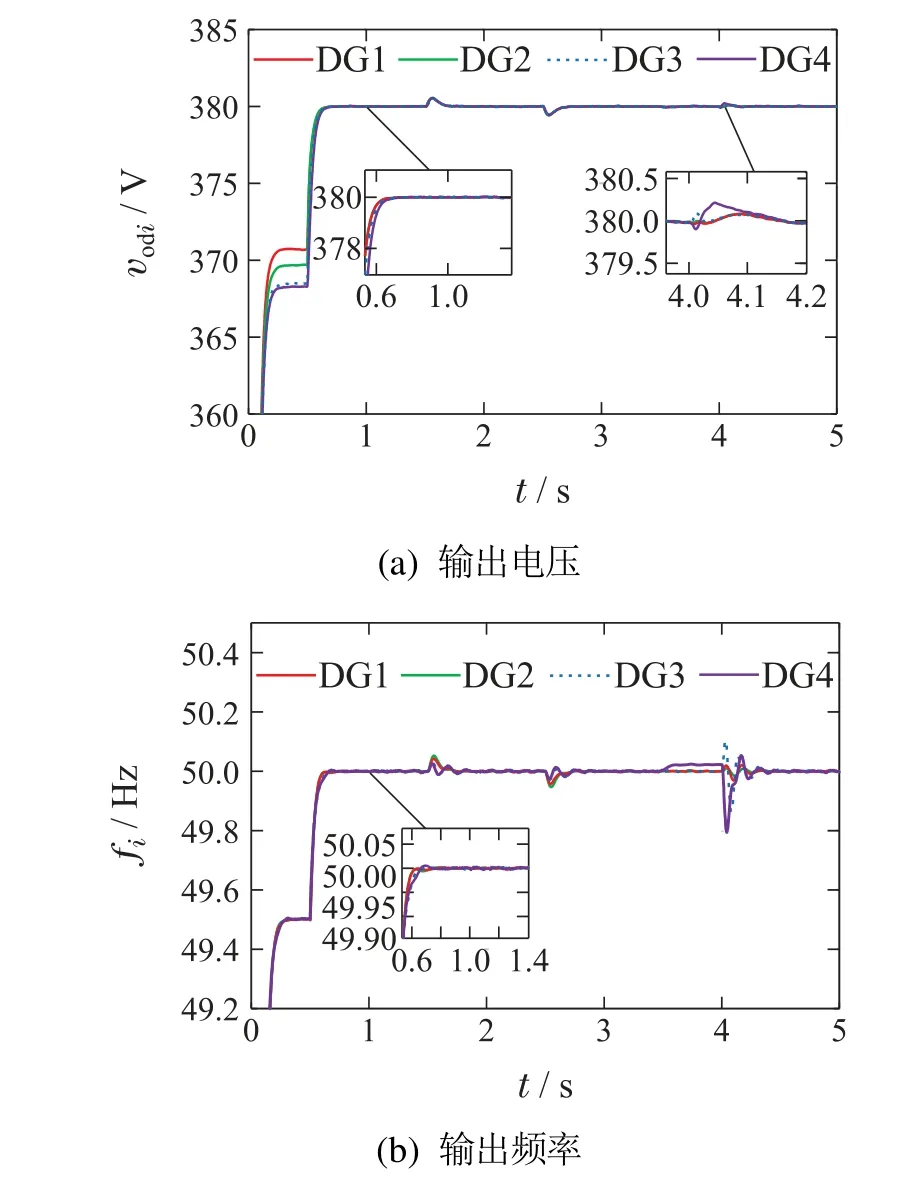
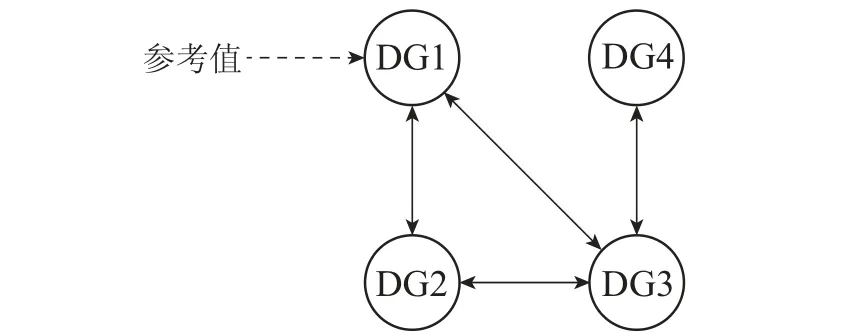
引理1∀p ∈R+,对于任意满足|s| 在交流微电网中,通常采用下垂控制对三相逆变器的输出电压和频率进行控制,以维持其稳定,称为一次控制[17].微电网中第i个逆变器的输出电压,电流d–q分量以及RLC滤波电路的动态特性如下[18]: 式中:vbdi和vbqi是公共耦合点处母线电压的d–q分量;vodi和voqi为RLC滤波电路输出电压的d–q分量;iodi和ioqi为RLC滤波电路输出电流的d–q分量;vidi和viqi为逆变器输入电压的d–q分量;iidi和iiqi为逆变器输出电流的d–q分量;Rfi,Lfi,Cfi为RLC滤波器的电阻、电感、电容;Rci,Lci为耦合线路的电阻和电感. 下垂控制方程如下: 式中:ωi为下垂控制产生的角频率;ωni和vni分别为输入角频率和电压;是频率和电压的下垂控制系数;Pi和Qi分别为低通滤波电路输出的有功功率和无功功率. 第2.3节中基于下垂控制的电压调节会产生一定的偏差,因此需对电压进行二次控制,以调节下垂控制产生的偏差.设输出为yi=vodi,输入为ui=vni,对式(4)求导并将式(2)代入整理得 利用一致性协议,设计分布式电源的输出电压误差函数为 式中y0i=vref为vodi的参考值(额定电压);bi≥0为控制增益Ni表示第i个控制器的通信邻域集. 式(12)等价于 定义下列误差: 式中αi是引入的虚拟控制量,将在后面设计. 对式(15)求一阶导数得 BLF是解决系统状态受限的控制方法[19],可通过构造适当的BLF 使系统稳定,并保证系统的状态始终在给定的约束范围内. 第1步 选择BLF保证系统状态满足预先设定的约束,即 式中pi为误差的边界值. 对式(17)求导可得 取虚拟控制量 式中c1i >0为可调参数. 将式(19)代入式(18)得 第2步 选择Lyapunov函数 对式(21)求导得 设计控制器如下: 式中:c2i≥0为给定正常数,是F1i的估计. 将式(24)代入式(22)得 由于F1i中涉及一些变量的导数,并考虑系统参数变化等情况,采用自适应模糊系统逼近方法处理.F1i可表示为 式中:ℜi是正定对角矩阵,µψi >0是可调参数. 选取Lyapunov函数为 由Lyapunov稳定性理论可知系统有界且收敛. 频率控制器的设计与电压控制器的设计类似,鉴于篇幅省略. 为了验证所提出的基于BLF和自适应模糊系统的二次电压和频率控制器的有效性,在MATLAB软件环境下,搭建每相电压为380 V频率为50 Hz的交流微电网[20].图1所示是交流微电网的简化通信链路框图,该框图由4个基于分布式电源的逆变器、4个负载、3条通信线路以及RL线路组成.图2是分布式电源的通信拓扑图. 图1 交流微电网的简化通信链路框图Fig.1 Simplified communication link block diagram of AC microgrid 图2 分布式电源的通信拓扑图Fig.2 Communication topology diagram of DG 为了方便对系统模型的运算,以及对分布式电源输出电压和频率的分析与对比,本文的参考电压vref为380 V,参考频率ωref为50 Hz.自适应模糊逻辑系统采用7个隶属度函数,即 控制器的可调参数选择为:c1i=50,c2i=100,c3i=50,ℜi=8,µψi=3,初始状态为零.取电压和频率的误差约束界值分别为:pi=20,gi=1,即满足:-2020,-1 表1 分布式电源的模型参数Table 1 Model parameters of DG 表2 负载和RL线路的一些参数Table 2 Some parameters of load and RL line 为了验证所提出的控制器能使系统的输出电压和频率与参考输入达成一致,使跟踪误差趋于零.设定:当t=0 s时,只采用下垂控制;当t=0.5 s 时,施加二次控制.随着系统运行,当t=1.5 s时,负载1增大50%;t=2.5 s时,负载1减小50%;t=3.5 s时,Line3断开;t=4 s时,Line3重新接上.二次电压和频率控制的控制效果如图3所示. 图3 负载变化下的分布式二次控制结果Fig.3 Distributed secondary control results under load changes 由图3可以看出,只采用下垂控制,电压和频率与标称值有一定偏差.在0.5 s时施加二次控制,经过0.2 s电压快速恢复到参考值,经过0.18 s频率快速恢复到参考值.当t=1.5 s和t=2.5 s时,系统负载发生变化,经过短暂调整,输出电压和频率仍跟踪参考输入,且波动小.当t=3.5 s通信中断和t=4 s 通信恢复时,输出电压经0.2 s恢复,频率经0.4 s左右恢复,且输出电压最大变化0.25 V,在受限界值20 V以内,波动小.输出频率最大变化0.21 Hz,也在受限界值1 Hz以内. 以上仿真结果表明,所提出的控制器可以迅速将输出电压与频率恢复到标称值,且达成一致,收敛速度快且跟踪性能好.无论在电压与频率的恢复期及负载变化时,输出电压和频率始终在受限范围360 V 为了验证所提出的控制器在通信拓扑变化时的性能,在t=1 s时改变通信拓扑结构,如图4所示.为了简化验证,本节只考虑一种情况,其他情况与之类似.系统输出电压和频率的仿真结果如图5所示. 图4 变化后的通信拓扑结构图Fig.4 Changes after the communication topology structure 图5 改变通信拓扑下的分布式二次控制Fig.5 Secondary control under changing communication topology 由图5可知,测试系统在t=1 s时,虽然通信拓扑结构发生了改变,但是分布式电源的输出电压与频率均在0.2 s左右快速达到参考值,且波动小,稳定性好.同时,输出电压和频率仍然在约束范围以内. 本文提出了一种基于BLF和自适应模糊系统的电压和频率二次控制器,补偿一次控制产生的偏差.采用BLF使输出电压和频率控制在约束范围内,采用自适应模糊系统对模型中的参数不确定,未知变量进行模糊逼近,提高了系统的鲁棒性.仿真结果表明,本文所提出的控制器无论在通信拓扑改变,还是在负载变化的情况下,电压与频率最终都能与参考输入保持一致.2.3 微电网建模及一次控制
3 分布式二次电压控制器设计
3.1 基于Backstepping法利用BLF设计控制器
3.3 稳定性证明
4 仿真与结果分析




4.1 二次电压与频率控制器的性能
4.2 改变通信拓扑后的控制性能

5 结论
