动态事件触发机制下二阶多智能体系统完全分布式控制

邓 甲,王付永,刘忠信,陈增强

(1.南开大学人工智能学院,天津 300350;2.南开大学智能机器人技术重点实验室,天津 300350)

1 引言

多智能体系统是由多个自主个体组成的群体系统,个体之间通过相互通信,以竞争或合作等方式,完成大量而复杂,单个智能体无法完成的工作.控制多个个体进行协调合作执行某一具体任务,在传感器网络[1–2]、多无人车系统[3]、卫星编队[4]等领域有着广阔的应用前景.因此,多智能体系统分布式协同控制问题,尤其是其中最基础的一致性问题,受到许多学者的广泛关注.多智能体系统的一致性是指系统中的智能个体在相互通信和局部协作下,调整更新自己的行为,最终使得每个智能体均能达到相同的状态[5–6].现有的一致性问题主要关注两个方面: 领导跟随一致性和无领导者协同一致性.其中,领导跟随问题要求跟随者的所有状态最终与领导者达到一致,即追踪到领导者的轨迹,这拓展了多智能体系统的工程应用.

在实际的工程应用中,智能体的通信资源和计算能力通常是有限的.为了减少系统能量耗散,事件触发机制被应用到多智能体系统中,即在合适的触发时刻,才进行数据采样、信息传输、控制信号更新等操作[7–8].传统的等周期采样是基于时间的触发,基于时间的触发往往会导致对有限的计算和通信资源的过度使用,而基于事件触发能提升资源利用效率,被认为是资源受限情况下一个重要的通信范式转变[9].事件触发控制按不同类型的触发函数可以分为基于常值的静态事件触发[10]、基于辅助动态变量或动态时钟的动态事件触发[11–15]、基于时间的事件触发[16–17]、基于边的事件触发[15,18–20]、基于等周期采样的事件触发[21–23]、基于自适应参数的事件触发[13,24–25]等.

事件触发机制的引入,一方面可以用于避免控制信号的连续更新,另一方面可以避免连续通信.文献[26]针对二阶多智能体系统的固定时间比例一致性问题给出了基于事件触发的控制协议,用于避免控制信号的连续更新,有效减小了系统能耗.但文献[26]测量误差以及触发函数的设计用到邻居的实时状态信息,因而难以有效避免连续通信,对通信资源的节约是非常有限的.本文致力于节省通信资源,设计基于事件触发的通信策略.在本文所提策略下,每个智能体只在自身触发时刻将自己的当前状态发送给邻居,智能体自身的触发函数和控制输入都不涉及邻居的实时状态信息,这有效避免了连续通信,降低了通信频次,从而达到了减少系统能耗的目的.

此外,对分布式多智能体系统中的每个智能体而言,系统节点总数、拉普拉斯矩阵的特征值等全局信息是难以获取的.现有的基于事件触发的很多成果都无法避免对全局信息的使用,文献[10,22,26–27]用到系统总节点数,文献[27–32]用到拉普拉斯矩阵的特征值.设计不依赖全局信息的完全分布式事件触发策略具有重要意义,文献[13,15,24]针对一般线性定常系统设计了完全分布式的事件触发机制,文献[33]针对m个具有一阶积分模型和n–m个具有二阶积分模型的智能体组成的异构系统设计了完全分布式的事件触发机制,但文献[24,33]的触发函数涉及邻居的实时状态信息.

目前,触发函数不使用邻居实时状态信息且不依赖任何全局信息的事件触发控制策略较少.文献[24]针对有向拓扑下的一般线性定常系统设计了一种自适应事件触发控制策略,但其使用联合误差,也就是说需要借助邻居智能体的实时状态信息来判断是否触发,而这与避免连续通信从而节省通信资源的初衷是相悖的.文献[10,22,26–32]所给出的事件触发机制都用到全局信息,不是完全分布式的.文献[13,15]分别针对无向拓扑下的一般线性定常系统设计了两类优秀的事件触发机制,满足: 1)触发函数不使用邻居实时状态信息,从而有效避免连续通信;2)触发策略不依赖任何全局信息,是完全分布式的;3)系统实现渐近一致性且不存在Zeno行为.文献[13,15]针对一般线性定常系统,具有较好的通用性,但其触发策略含有较多参数,且需求解代数里卡蒂方程,其所提事件触发控制策略虽然适用于较为简单的一阶积分系统或者二阶积分系统,但注意到系统模型简单却并不会使得控制策略简化,较多的参数将在实际应用中带来麻烦,同时代数里卡蒂方程的计算也将消耗额外的计算资源.设计参数较少且易调的新型事件触发控制策略具有重要意义.

动态事件触发机制相较于其他类型的触发机制具有更高的灵活性,并且通常有着更宽松的触发条件,因而能在更大程度上减少系统能耗[9].现有的动态事件触发机制主要有两类,一类是基于动态时钟的事件触发机制[11–13];另一类是基于辅助动态变量的事件触发机制[14–15].基于动态时钟是指智能体的触发时刻由某个非负的动态变量来决定.当该动态变量为零时,触发事件并重置该变量为某个正值,事件间智能体根据状态误差来更新该变量,当该变量再次为零时再次触发事件.该动态变量具有时钟的特点,称其为动态时钟,智能体的触发时刻是由该动态时钟来决定的.基于辅助动态变量的事件触发机制是指智能体触发函数的阈值条件基于某个辅助动态变量,该辅助动态变量并不直接决定触发时刻,而是监测到状态误差函数大于该动态阈值条件时触发事件.与静态阈值,基于时间的阈值相比,基于辅助动态变量的阈值更灵活,这在避免Zeno行为方面具有优势.此外,辅助动态变量进一步放宽了阈值条件,因而进一步降低了触发频次,更大程度上节省了通信资源.文献[11–13]分别针对一阶积分系统、二阶积分系统、一般线性定常系统设计了基于动态时钟的事件触发机制.文献[14]针对一阶积分系统设计了基于辅助动态变量的完全分布式事件触发机制,本文受其启发,将其进一步扩展到二阶积分系统.文献[15]针对一般线性定常系统设计了基于辅助动态变量的事件触发机制,但其涉及多个自适应参数且无法避免对代数里卡蒂方程的计算,这将额外消耗大量的计算资源.另外,文献[15]触发函数中待确定的参数太多,实际应用中可能较难调出合适的参数.本文与之相比,一方面系统模型不同,另一方面设计了参数较少且易调的新型事件触发机制,并在仿真示例中简单给出了选取相关参数的方法.

本文针对二阶多智能体系统,在无领导者和有领导者两种情形下,分别设计了基于辅助动态变量的动态事件触发机制,主要有如下特点和贡献: 1)文献[17,24,27,34–37]未避免对邻居状态的实时检测,本文与之相比,触发函数和控制协议都未用到邻居的任何实时状态信息,有效避免了连续通信,节省了通信资源;2)文献[10,22,26–32]需要使用系统总节点数、拉普拉斯矩阵特征值等全局信息,本文触发函数和控制协议包括相关参数的设计都不依赖通信拓扑网络的任何全局信息,是完全分布式的;3)文献[31,38–39]在排除Zeno行为的前提下只能实现在有界区间波动的实际一致性,本文设计的事件触发机制可以保证系统实现渐近一致性且不存在Zeno 行为;4)文献[13,15]所设计的事件触发控制参数较多,不易调整,本文致力于设计参数较少且容易调整的事件触发控制策略.

本文后续的内容安排如下: 第1部分介绍必要的预备知识,描述具体的模型以及问题;第2部分分别针对无领导和领导跟随的情况提出事件触发一致性控制策略,并证明所提出的策略下系统实现渐近一致性,且不存在Zeno行为;第3部分分别针对无领导和领导跟随的情况,给出数值仿真示例进一步验证结果的有效性,并分析主要参数对触发频次和收敛性能的影响,给出确定参数的方法;第4部分对全文做出总结.

文中的相关符号说明如下: Rm和Rn×m分别表示m维列向量和n×m维矩阵空间,向量元素和矩阵元素都为实数;0n×n表示n×n的零矩阵;diag{a1,a2,···,an}表示以a1,a2,···,an为对角元素,其他元素全为0的n×n矩阵.

2 预备知识和问题描述

这部分介绍必要的图论知识、系统模型、问题描述以及相关的符号定义.

2.1 图论

多智能体系统的通信拓扑图G=(V(G),E(G)),其中V(G)={1,2,···,n}表示节点的集合,E(G)⊆{(i,j)|i,j ∈V(G)}表示边的集合.边(i,j)表示节点j能够收到节点i传输的信息,aij表示边(j,i)的权值,若节点j到节点i存在边,则aij >0,否则aij=0,对于无向图aij=aji.图的邻接矩阵定义为A=[aij]∈Rn×n.

对上述多智能体系统增添一个领导者,用D=diag{d1,···,dn}表示每个跟随者i ∈V(G)与领导者之间的通信关系,如果智能体i能收到领导者的信息,那么di >0,否则di=0.显然,对无领导者模型,可以认为D=0n×n.

2.2 问题描述

考虑由n个具有二阶积分模型的智能体组成的无领导者二阶多智能体系统.第i个智能体的动力学模型如下:

其中:xi(t)∈Rm表示智能体i的位置状态,vi(t)∈Rm表示智能体i的速度状态,ui(t)∈Rm表示智能体i的控制输入.

定义1对于所有的智能体i ∈V,如果存在控制协议ui(t),使得系统在任意初始状态下,对任意的i,j ∈V都满足

则称系统(1)实现了无领导者渐近一致性.

考虑由1个领导者和n个跟随者组成的领导跟随二阶多智能体系统.第i个跟随者的动力学模型同式(1),领导者的动力学模型如下:

其中:x0(t)∈Rm表示领导者的位置状态,v0(t)∈Rm表示领导者的速度状态,领导者的控制输入为0.

定义2对于所有的智能体i ∈V(G),如果存在控制协议ui(t),使得系统在任意初始状态下,对任意的i ∈V(G)都满足

则称系统(1)(3)实现了领导跟随渐近一致性.

为了方便分析,本文给出的结果都是基于一维的(m=1),但由于每一维之间是相互独立的,因此,很容易利用Kronecker乘积将结果拓展到m维.

3 完全分布式动态事件触发一致性

为了节省通信资源,为每个智能体设计合适的触发函数,使得每个智能体只在自身触发时刻向邻居广播自身状态信息.也就是说,对每个智能体而言,邻居的实时状态信息是未知的,那么每个智能体自身的控制协议以及触发函数都只能使用邻居在触发时刻的状态信息而不能使用邻居的实时信息.下面分别针对有无领导者两种情况给出具体的设计和证明.

3.1 无领导者一致性

用表示智能体i第k次事件触发时刻.对系统(1)给出基于事件触发的控协议如下:

注1此处控制器的设计对位置状态采用一阶保持,也就是说,在事件间,控制器根据上一触发时刻的值以预测和估计的形式给出比零阶保持更合适的控制信号,这将进一步降低通信频次,从而达到节约通信资源的目的.如果位置状态采用零阶保持,相应的位置测量误差定义为(t)=(t)-xi(t),不会对后续的理论分析造成任何影响,但这样虽然能避免控制信号的连续更新,却会使得触发更加频繁,将消耗更多的通信资源.本文致力于节省通信资源,因而选择对位置状态进行一阶保持这一设计方法.

给出如下触发函数:

其中:θi >0,βi >0 为参数;χi(t)为辅助动态变量,χi(0)>0.

注2触发函数(8)中的触发阈值基于辅助动态变量χi(t),因此所设计的事件触发机制称为基于辅助动态变量的动态事件触发机制.如果将阈值θiχi(t)替换为静态阈值c(c>0),系统将实现有界区间内波动的实际一致性.如果将阈值θiχi(t)替换为基于时间的函数αe-βt(α,β >0),系统也能实现渐近一致性,但结合式(18)可知,相较于基于时间的阈值,基于辅助动态变量的阈值进一步放宽了触发条件,因此能进一步降低触发频次.

注31)本文设计的事件触发机制(8)–(9)不涉及邻居的实时状态信息,这有效避免了连续通信.智能体i在第k次触发后,只需借助邻居智能体j在触发时刻传输来的信息即可确定自身的下一触发时刻.文献[26,37]也针对二阶积分系统设计了事件触发机制,但其选用了联合测量误差,智能体i需要借助邻居智能体的实时状态信息xj(t)和vj(t)来确定下一触发时刻.这意味着每个智能体都需要实时向邻居发送自身的状态信息,而这与节省通信资源的初衷是相悖的;2)本文设计的事件触发机制包括相关参数的选取都不依赖系统节点总数以及拉普拉斯矩阵特征值等全局信息,是完全分布式的.对分布式系统,尤其是系统规模较大的时候,对每个智能体而言,拉普拉斯矩阵特征值等全局信息是很难获取的.文献[10,22,26–32]所设计的事件触发机制都涉及对全局信息的使用,本文设计的完全分布式事件触发控制策略具有扩展性好的优势;3)本文设计了参数较少且易调的新型事件触发机制.文献[13,15]分别针对一般线性定常系统设计了两类不同的事件触发机制,但其待确定的参数很多,且涉及代数里卡蒂方程的计算以及自适应参数的更新.即使针对较为简单的系统模型,文献[13,15]设计的事件触发机制仍有很大的计算量,且过多的参数会在实际应用中带来麻烦.本文设计了参数较少且易调的新型事件触发机制,并在数值仿真部分简要给出了选取这些参数的经验方法.

为了更简洁的表示,变量中的参数t通常被省略,同时定义以下向量:

定理1假设固定通信拓扑图G为无向连通图,多智能体系统(1)在控制器(5)和触发函数(8)的作用下,在任意初始状态下均能实现无领导者渐近一致性.

证选定李雅普诺夫函数为

结合式(11)进一步可以得到

结合式(11)(15)容易得到

触发函数式(8)的设计使得fi(·)≤θiχi(t)始终成立,容易得到

进一步可以得到

定理2假设固定通信拓扑图G为无向连通图,多智能体系统(1)在控制器(5)和触发函数(8)的作用下,在任意初始状态下系统均不存在Zeno行为.

为了更简洁的表示,定义

容易得到fi(·)≤θiχi(t)的一个充分条件是

进一步得到

3.2 领导跟随一致性

对系统(1)(3)给出基于事件触发的控协议如下:

其中:ϑi >0,γi >0为参数;ψi(t)为辅助动态变量,ψi(0)>0.

定理3假设固定通信拓扑图G为无向连通图,多智能体系统(1)和(3)在控制器(23)和触发函数(24)的作用下,在任意初始状态下均能实现领导跟随渐近一致性.

结合式(14)(28)容易得到

结合式(25)–(26)(29),进一步得到

由式(24)(26)不难得到

证毕.

定理4假设固定通信拓扑图G为无向连通图,多智能体系统(1)(3)在控制器(23)和触发函数(24)的作用下,在任意初始状态下系统均不存在Zeno行为.

为了更简洁的表示,定义为

推论1假设固定通信拓扑图G为无向连通图,多智能体系统(1)(3)的领导者如果发生通信故障,跟随者在控制器(23)和触发函数(24)的作用下将实现无领导者一致性,且系统不存在Zeno行为.

证观察控制器(5)(23)以及触发函数(8)(24),容易发现当di=0时,式(23)退化为式(5),式(24)退化为式(8).同时,无领导者系统可以认为是有领导者系统在D=0n×n时的特殊情况.因此,有领导者多智能体系统(1)(3)在控制器(23)和触发函数(24)的作用下,如果领导者发生通信故障,那么跟随者将按照无领导者模型实现一致性,且系统不存在Zeno行为.证毕.

4 数值仿真

这部分首先通过数值仿真示例来验证了理论结果的正确性和有效性.随后,分析讨论了所设计的触发机制中相关参数对触发频次和收敛性能的影响,给出了选取这些参数的经验方法.最后,通过对比实验验证了: 控制输入中位置状态采用一阶保持相较于零阶保持进一步降低了通信频次;基于辅助动态变量的动态事件触发机制与基于静态阈值的传统触发机制相比具有更高的灵活性,在排除Zeno行为的同时能确保系统具有不错的收敛性能.

4.1 结果验证

首先考虑无领导者的情形.考虑5个具有二阶积分模型的智能体组成的多智能体系统,5个智能体间的通讯拓扑图如图1所示.

图1 无领导者系统的通信拓扑图Fig.1 The communication topology of the leaderless system

智能体初始状态:x(0)=[0 1 2 3 4]T,v(0)=[0.8 1 0.3-0.6 0.8]T.相关参数设定为:µ=3,θi=0.1,βi=0.4,χi(0)=3,其中i=1,2,···,5.仿真结果如图所示.图2展示了每个智能体的速度状态随时间的变化,图3展示了每个智能体的位置状态随时间的变化,结果表明: 该多智能体系统实现渐近一致性,所设计的控制策略是有效的.

图2 无领导者: 速度状态轨迹Fig.2 Leaderless: The trajectories of the speed state

图3 无领导者: 位置状态轨迹Fig.3 Leaderless: The trajectories of the position state

图4展示了每个智能体的触发时刻,也就是每个智能体广播自身状态信息的时刻,图中可以看出每个智能体的触发时刻是异步的,同时不存在Zeno行为.

图4 无领导者: 触发时刻Fig.4 Leaderless: Event-triggered instants

下面考虑有领导者的情形.考虑1个领导者和5个跟随者组成的二阶多智能体系统,这6个智能体间的通信拓扑图如图5所示.

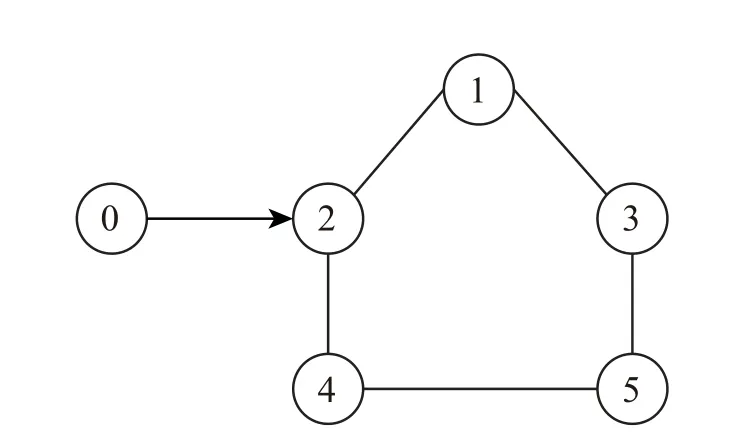
图5 领导跟随系统的通信拓扑图Fig.5 The topology of the leader-follower system

跟随者初始状态置为:x(0)=[0 1 2 3 4]T,v(0)=[0.8 1 0.3-0.6 0.8]T,领导者初始状态置为:x0(0)=2,v0(0)=0.1.选 取µ=2.5,ϑi=0.2,γi=0.4,ψi(0)=1,其中i=1,2,···,5.

仿真结果如图所示.图6和图7分别展示了每个智能体的速度以及位置状态随时间的变化.结果表明,跟随者最终都能成功跟踪领导者的状态,实现了领导跟随渐近一致性,所设计的控制策略是有效的.图8展示了每个跟随者的触发时刻,触发时刻是异步的并且不存在Zeno行为.跟随者只在自身触发时刻广播自身的状态信息,有效减少了系统能量耗散.

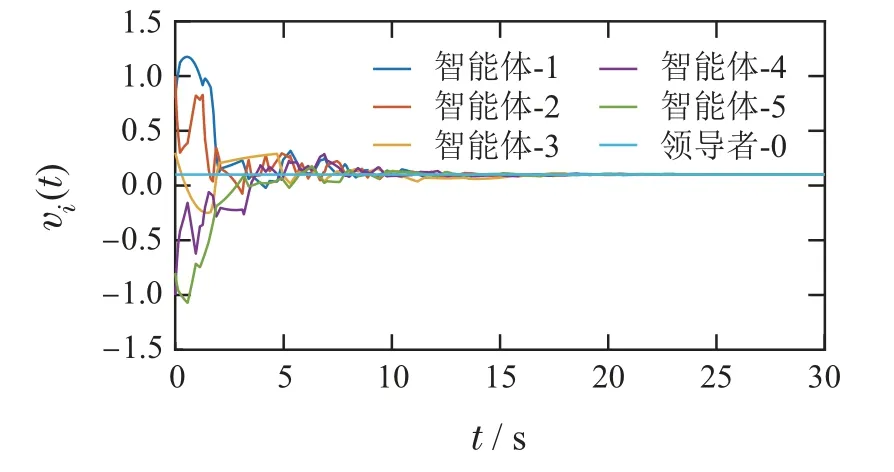
图6 领导跟随:速度状态轨迹Fig.6 Leader-Follower: The trajectories of the speed state

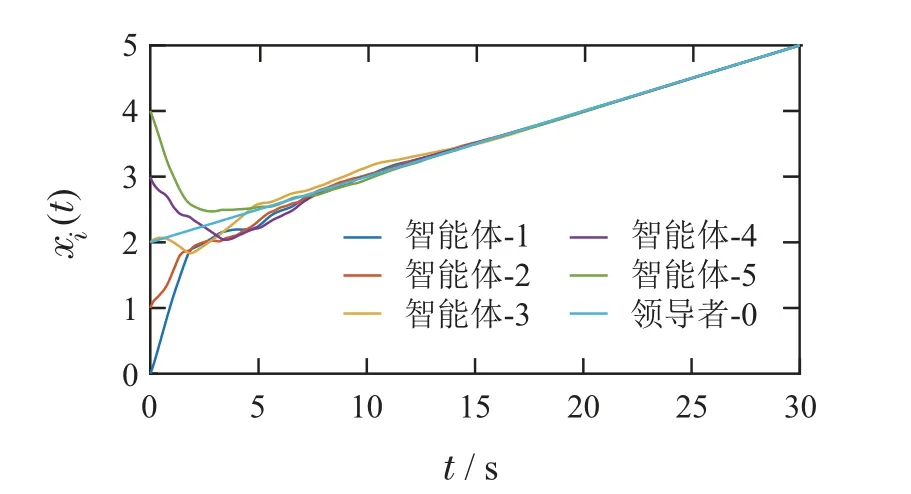
图7 领导跟随:位置状态轨迹Fig.7 Leader-Follower: The trajectories of the position state

图8 领导跟随:触发时刻Fig.8 Leader-Follower: Event-triggered instants

4.2 参数分析

以无领导者的情形为例,分析参数βi,θi以及辅助动态变量的初值χi(0)对触发频次和收敛速度的影响.为了便于调整参数,各智能体可选用同一套参数,即θi=θ,βi=β,χi(0)=χ(0),i=1,2,···,5.固 定其余参数不变,系统总的触发次数随参数χi(0),θi,βi变化的曲线分别如图9–11所示.

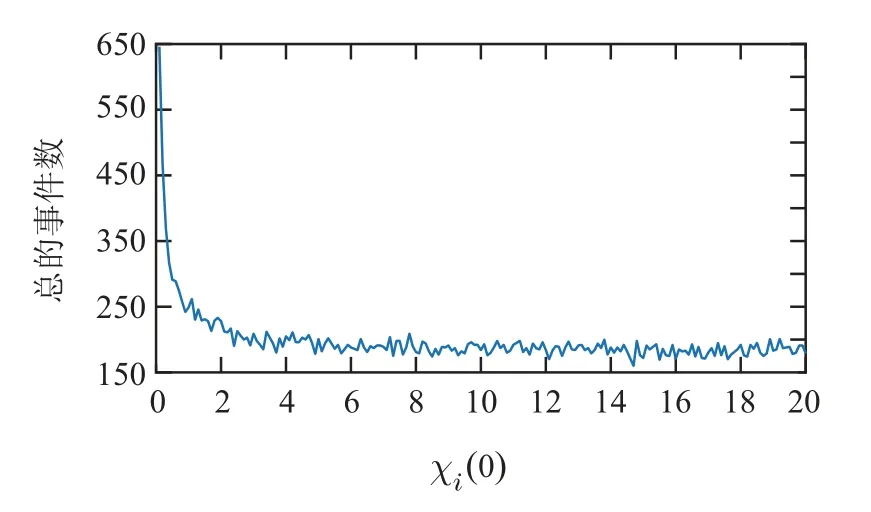
图9 无领导者: 调整参数χi(0)时总的事件数Fig.9 Leaderless: The total number of events when adjusting the parameter χi(0)

结合式(8)–(9)可知,χi(0)和θi共同决定触发阈值的初值,βi影响阈值的下降速度,θi同时影响阈值的初值和下降速度.阈值下降速度越快意味着触发越频繁,动态收敛性能越好,但也可能引起资源的过度消耗.合适的阈值下降速度可以在几乎不影响收敛性能的情况下极大减少对通信资源的消耗.如图9所示,阈值的初值越小意味着前期触发越频繁,太小的初值会使得触发很频繁.如图10–11所示,当动态阈值的初值较大时,触发频次主要由阈值下降速度来决定.

图10 无领导者: 调整参数θi时总的事件数Fig.10 Leaderless: The total number of events when adjusting the parameter θi

图11 无领导者: 调整参数βi时总的事件数Fig.11 Leaderless: The total number of events when adjusting the parameter βi

实际应用中,可以先将辅助动态变量的初值χ(0)置为一个相对比较大的值,将θ置为相对较小的值,随后尝试调整β即可很快调出合适的参数.针对有领导的情形,参数ϑi,γi以及ψi(0)的选取方法与无领导情形下的选取方法类似,本文所设计的事件触发机制具有参数较少且易调的优点.

4.3 对比实验

本文设计的基于事件触发的控制协议(5)(23)中,位置状态均采用了一阶保持.这意味着在事件间,控制器根据上一触发时刻的值以预测和估计的形式给出了比零阶保持更合适的控制信号,从而进一步降低了触发频次,节省了通信资源.下面以第4.1节中有领导者的情形为例,给出位置状态分别采用一阶保持和零阶保持的对比实验结果.

表1给出了30 s内各智能体的触发次数以及5个智能体的总触发次数.两种情形下5个智能体的触发时刻如图12所示.结果表明,位置状态采用一阶保持的情形下,每个智能体的触发次数都低于零阶保持的情形,触发频次的降低进一步节省了通信资源.

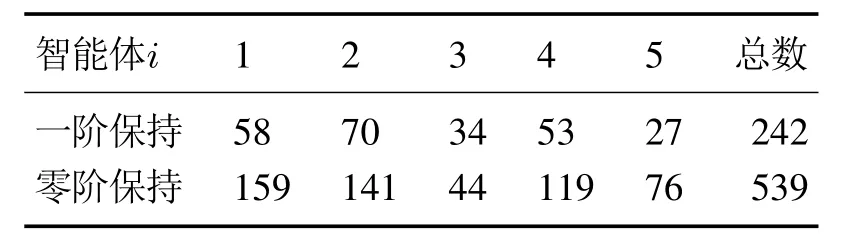
表1 位置状态分别采用一阶保持和零阶保持的情形下各智能体的事件触发次数Table 1 The number of events of each agent when the position state adopts the first-order hold and the zero-order hold,respectively

图12 位置状态分别采用一阶保持和零阶保持的情形下各智能体的触发时刻Fig.12 The event-triggered instants of each agent when the position state adopts the first-order hold and the zeroorder hold,respectively

传统的静态事件触发机制其阈值函数是某个常数c(c≥0),本文设计的动态事件触发机制阈值函数为θiχi(t).动态阈值与传统的静态阈值相比具有更高的灵活性.阈值函数基于常数c时,若c=0,系统的触发频次将非常密集,并且难以排除Zeno行为;若c>0,则系统只能实现有界区间内波动的实际一致性.下面以第4.1节中有领导者的情形为例,给出静态事件触发下c=0.1时的仿真结果.

图13–14分别展示了多智能体系统在静态事件触发机制下的速度状态轨迹和位置状态轨迹.结果表明,与静态事件触发机制相比,本文设计的动态事件触发机制不仅有效排除了Zeno行为,而且确保了系统仍有不错的收敛性能,系统实现渐近一致性而不是有界区间内波动的实际一致性.

图13 静态事件触发机制下各智能体的速度状态轨迹Fig.13 The speed state trajectory of each agent under the static event-triggered mechanism

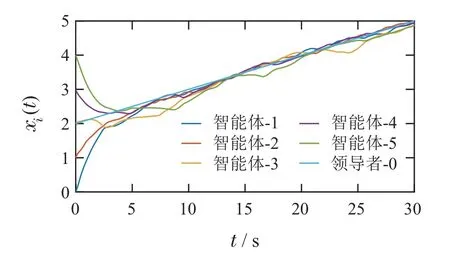
图14 静态事件触发机制下各智能体的位置状态轨迹Fig.14 The position state trajectory of each agent under the static event-triggered mechanism

5 结论

本文研究了二阶多智能体系统的一致性问题,引入事件触发机制,致力于降低通信频次.分别针对无领导者和有领导者的情形,设计了基于辅助动态变量的完全分布式事件触发控制策略,该策略具有参数较少且易调等特点.首先,为每个智能体设计了不依赖邻居实时状态信息的控制信号.每个智能体只获取邻居触发时刻的状态信息,只根据自身的状态和邻居触发时刻的状态更新控制信号;然后,为每个智能体设计了基于辅助动态变量的完全分布式事件触发函数,用于确定每个智能体的触发时刻.触发函数只涉及智能体自身状态和邻居上一触发时刻的状态信息,不涉及邻居的实时状态信息,也不依赖系统节点总数,拉普拉斯矩阵特征值等全局信息;最后,每个智能体通过自身的触发函数来确定触发时刻,只在触发时刻向邻居广播自身的状态信息,控制器根据智能体自身的状态和邻居触发时刻的状态信息更新控制信号.证明了在该控制策略下,二阶多智能体系统实现渐近一致性,并且不存在Zeno行为.未来将针对有向通讯拓扑的情形做进一步的研究和探讨.