面向任务的重叠联盟结构生成计算复杂性

张国富 宋晓晓苏兆品岳 峰

(1.合肥工业大学计算机与信息学院,安徽 合肥 230601;2.合肥工业大学智能互联系统安徽省实验室,安徽 合肥 230009;3.合肥工业大学工业安全应急技术安徽省重点实验室,安徽 合肥 230601)

1 引言

联盟形成是多智能体系统中最基本、最重要的交互与合作形式.形成一个协作联盟可以让一组资源不足的agent通过共享资源和合作完成单个智能体不可能完成的任务,已在无线网络[1]和电力调度[2]等领域得到广泛应用.然而,为一批给定的任务分配最合适的协作联盟在计算复杂性上具有很大的挑战性,其核心是确定将形成哪些联盟,以及哪些联盟最有利于有效和稳定的完成给定的任务[3].

为了解决上述问题,在人工智能基础研究领域涌现了一批优秀的联盟形成模型和算法,如联盟结构生成[4]、技能结盟博弈[5]、资源结盟博弈[6–7]、重叠联盟形成博弈(overlapping coalition formation games,OCFGs)[8–9]等.具体来说,经典的联盟结构生成问题旨在寻找智能体集的最优划分,以使特征函数返回的联盟值总和最大,但通常和任务无关,这使得联盟结构生成理论和方法难以在实际中应用.

为了使联盟形成更贴切实际,技能结盟博弈、资源结盟博弈和OCFGs将联盟值与其完成的任务或实现的目标联系起来.此外,上述模型还允许一个联盟同时承担多个不同的任务,这意味着每个智能体可以变相的参加不同的任务.不过,技能结盟博弈和资源结盟博弈都强制要求每个智能体都必须且只能加入一个联盟,无论其能力或资源情况如何,这大大降低了智能体响应任务的积极性,导致资源利用率极低,并限制了联盟的协作灵活性.应该看到的是,拥有足够资源或强大能力的智能体完全可以加入更多的不同联盟,以求解更多的任务、追求更多的效用.为此,OCFGs提供了最具扩展性和灵活性的协作机制,规定每个智能体都可以参与所有可能的联盟,以自由竞争所有的任务.这种协作方式可以最大限度的利用智能体的资源,在时间有限、资源稀缺但需求量很大的实际场景中具有重要意义[10].但是,这种合作的灵活性也极大的增加了问题的复杂性和计算负担,使得联盟决策极其困难.

需要指出的是,在大多数实际应用场景中,智能体的行为通常是由任务驱动的,即智能体仅会为符合其自身利益或感兴趣的任务贡献资源.例如,在协作运输[11]中,每辆卡车往往只会响应附近的运输订单,以尽可能降低运输成本.在无线网络[1]中,为了节省能量和延长网络寿命,每个节点倾向于仅在其当前感知范围内跟踪目标,而不会主动增加发射功率以感知未知目标.此外,当一次涉及的智能体数或任务数较大时,一个突出的问题是如何减少联盟的规模和可能的联盟结构数,以有效利用智能体资源,节省计算成本,提高任务求解性能.在这种情况下,合理的选择通常是限制联盟的大小[12],而通过限制每个智能体可以响应的任务子集规模是一个非常贴切实际的选择[7].

基于上述背景,本文从并发多任务视角出发,根据智能体当前的资源状况和每个智能体的兴趣集,致力于如何划分任务子集给智能体去承担,从而实现社会效用最大化.本文的主要贡献有:

1)本文提出了一种新的面向任务的重叠联盟结构生成(overlapping coalition structure,OCS)模型.与已有工作不同的是,在所提的模型中,联盟结构中的联盟是智能体集合的一个覆盖,而联盟结构承担的任务是任务集的一个划分子集,适用于各种并发多任务调度场景,即根据给定的批量并发任务,在考虑智能体资源状况的前提下,决策选择哪些智能体组成哪些联盟去执行哪些任务;

2)本文对所提模型的解空间和计算复杂性进行了理论分析.研究发现,判断重叠联盟结构的成功性是一个P问题,即是多项式时间可解的,而搜索最优重叠联盟结构是一个NP完全问题,即是多项式时间难解的;

3)为了验证上述结果,本文基于流网络分别设计了相应的孤立联盟、重叠联盟、重叠联盟结构成功性判别算法和最优重叠联盟结构生成算法.分析结果表明,判别孤立联盟、重叠联盟、重叠联盟结构的成功性的时间复杂度均与智能体数和任务数呈多项式关系,而搜索最优重叠联盟结构的时间复杂度与智能体数和任务数呈指数关系.

2 数学建模

定义1在面向任务的环境下,每个重叠联盟是一个二元组(C,V),其中,C ⊆A表示一组智能体子集,满足C∅,且C中的成员可能是重叠的,即还会参加其他的联盟;V ⊆T表示该联盟的集体任务集.

定义2在任务偏好下,每个OCS是一组重叠联盟的集合,其中的智能体子集是A的一个覆盖,且每个重叠联盟承担互不相同的任务子集,如图1所示,满足:这些任务子集之间没有任何交集;这些任务子集中最多只有一个可以为空集,这时所有的任务都已被其他联盟承担,或者剩余的智能体子集已无力承担任何子任务.假设OCS={(C1,V1),···,(Cq,Vq)},q ∈N为OCS 中的重叠联盟个数,则

图1 面向任务的重叠联盟结构示意图Fig.1 Diagram of the task-oriented OCS

1)Cl ⊆A,Cl=∅,∀l ∈{1,···,q},即每个Cl都是A的一个非空子集;

2)Cx ∩Cy∅,∃x,y ∈{1,···,q},xy,即各Cl之间可能存在重叠的智能体成员;

4)Vl ⊆T,∀l ∈{1,···,q},即每个Vl都是T的一个子集;

5)Vx ∩Vy=∅,∀x,y ∈{1,···,q},xy,即各Vl之间不相交;

6)|{Vl|Vl=∅}|≤1,l ∈{1,···,q},即所有的Vl中至多只有一个为空集.

定义3OCS中的联盟(Cl,Vl)是成功的,当且仅当

1)Vl=∅,即不承担任务的联盟毫无实际意义;

2)∀aj ∈Cl,Tj ∩Vl∅,即Cl中的每个智能体成员都能够在集体任务集Vl中找到一个其感兴趣的子任务;

3)Vl中的每个子任务都能够被Cl顺利完成;

4)(Cl,Vl)内部以及和OCS中的其他联盟之间没有任何资源冲突.

定义4OCS是成功的,当且仅当OCS中至少包含一个成功联盟.

从上述定义可以看出,对于一个OCS,所有的智能体子集Cl恰好构成A的一个覆盖,所有的集体任务集Vl构成了任务集T的一个划分子集.OCS中的每个联盟要想成功,不仅需要考虑其内部,还需要考虑联盟之间是否存在资源冲突.当联盟内部因资源竞争而找不到可行的资源分配方案时,该联盟就不可能成功.另一方面,当几个不同联盟因为重叠成员而存在资源冲突时,与重叠成员相关联的这些联盟均不可能成功.

如果联盟(Cl,Vl)是成功的,则其联盟值为

否则,v(Cl,Vl)=0.进一步的,OCS的值为

基于上述描述,最优OCS生成问题就是寻找一个OCS∗,利用有限的智能体资源谋求社会效用最大化,即

其中表示在A和T上产生的所有OCS的集合.

3 计算复杂性分析

在本节,本文将分析面向任务的OCS生成问题的解空间和计算复杂性,有如下结果.

命题1OCS={(C1,V1),···,(Cq,Vq)}中包含的重叠联盟数q≤m+1.

证由定义2可知,所有的集体任务集都没有交集并且最多只能有一个集体任务集为空,因此有如下两种情况: 首先,所有的集体任务集均不为空集,则OCS中最多只有m个联盟,也就是每一个子任务ti构成一个集体任务集Vl,因此有q≤m;其次,当有且仅有一个集体任务集为空时,根据前面的分析,其他也最多只有m个集体任务集,此时每个集体任务集Vl里面有且仅有一个任务ti,因此有q-1 ≤m.综合两种情况,可得q≤m+1.证毕.

命题2OCS中的C1,···,Cq构成了智能体集合A的一个覆盖,其可能的覆盖数为.

证已知给定n个智能体,有2n-1个非空智能体子集[6].在OCFGs中,每个智能体可能同时参加这2n-1 个子集.不失一般性,对于OCS={(C1,V1),···,(Cq,Vq)},假设C1有2n-1 种情况,那么C2有2n-2种情况,以此类推,Cq只剩2n-q种可能.因此,可能的覆盖数为

命题6判别OCS 中任意联盟(Cl,Vl)是否成功是一个P问题.

证对于给定的任意(Cl,Vl),只有两种情况:(Cl,Vl)是孤立的,即不包含任何重叠成员;(Cl,Vl)是一个重叠联盟,其成员还参加了其他联盟.如果(Cl,Vl)是一个非重叠联盟,首先需要判断Vl是否为空集.如果Vl不为空集,则再检查Vl是否被Cl中的每个智能体感兴趣,即对∀aj ∈Cl,检查Tj ∩Vl∅是否成立.显然,上述操作可以在多项式时间内完成.其次,需要判断是否能够找到一个可行的资源分配方案使得Cl能够顺利完成Vl.也就是说,对∀ti ∈Vl,都有对其感兴趣的智能体贡献资源完成它,且子任务之间不存在任何资源冲突.由于|Cl|,|Vl|和r均是有界的,这种资源分配尝试也很容易在多项式时间内完成.另一方面,如果(Cl,Vl)是一个重叠联盟,将与之关联的所有集体任务集非空的重叠联盟放在一起进行考虑,检查的步骤与上面类似,首先检查智能体是否对任务集感兴趣,然后检查能否在几个重叠联盟之间找到一个可行的资源分配方案,使得每个重叠联盟都能够得到满足.由于考察的重叠联盟数是有限的,每个重叠联盟的智能体子集和集体任务集也是有限的,这种资源分配也可以在多项式时间内完成.综上可得,判别联盟(Cl,Vl)是否成功是多项式时间可解的,即是一个P问题.

证毕.

命题7判别OCS是否成功也是一个P问题.

证一个OCS最多包含q≤m+1个重叠联盟,显然|OCS|是有界的.根据定义4可知,只要OCS包含一个成功联盟(Cl,Vl),则OCS就是成功的.而根据命题6可知,判别(Cl,Vl)是否成功是多项式可解的.因此,判别OCS是否成功也是多项式时间可解的,即是一个P问题.证毕.

命题8搜索最优OCS是一个NP完全问题.

证根据式(3),搜索最优OCS 的决策问题可以描述为在智能体集A、任务集T和一些联盟(C,V)(C ⊆A,V ⊆T)下,是否存在一个值至少为Y的OCS?首先,需要检查这个决策问题的NP性,这需要猜测一个成功的OCS,因为只有成功OCS才可能有联盟结构值.由命题1可知,OCS中最多有m+1个重叠联盟,再根据命题6和命题7可知,验证每个联盟是否成功并且计算联盟结构值都是可以在多项式时间内完成的.因此,上述决策是一个NP问题.其次,还需要进一步证明上述决策是一个NP难问题.根据规约法,将NP完全问题集中的0–1背包问题约简为上述决策问题.0–1背包问题可表示为:给定一个容量为Ω的背包和一组物品{g1,···,gm},每个物品gi有一个体积wi和一个价值vi,是否存在一个序列{x1,···,xm}∈{0,1}m,使得? 为此,本文使用如下约简方法.让Tj=T,r=1,Y=Z,=Ω,且对∀i ∈{1,···,m},ti=gi,Di=wi,µi=vi.可以看到,OCS中的每个智能体子集C恰好对应一个已选择并放置在背包中的物品ti.|V >1|意味着背包中为V的每个任务分配的联盟是相同的.因此,存在一个值至少为Y的OCS 当且仅当存在一个序列{x1,···,xm}∈{0,1}m可以满足≤Ω和≥Z.综上可得,搜索最优OCS是一个NP完全问题,即是多项式时间难解的.证毕.

4 成功性判别算法

要想计算OCS的值,就必须明确OCS中的联盟是否成功.根据前面的分析,OCS中的联盟分为两种情况: 一种是孤立联盟,即没有任何交叉成员;另一种是重叠联盟,即部分智能体成员还参加了其他联盟.显然,针对孤立联盟,只需要检查联盟内部是否能找到一个合理的资源分配方案,而针对重叠联盟,不仅需要检查联盟内部,还需要检查几个关联的重叠联盟在交叉智能体成员上是否有资源冲突.显然,这两种情形需要分别处理.在本节,本文针对OCS中的孤立联盟和重叠联盟分别设计了相应的成功性判别算法,并分析了每个算法的时间复杂度,探讨了一些决策问题的复杂性与智能体数和任务数的关系,以进一步验证前面命题的分析结果,即是否真的存在多项式时间算法可以判别联盟的成功性,以及搜索最优重叠联盟结构是否是多项式时间难解的,本文的结论见表1.需要指出的是,这些判别算法并不能求解出一个成功的联盟,只能用于判断一个业已形成的联盟是否成功.下面,本文将针对表1中的结果进行详细阐述.

表1 计算复杂性分析结果Table 1 Main complexity results relating to OCS

4.1 孤立联盟的成功性判别

给定一个孤立联盟(Cl,Vl),很难直接看出(Cl,Vl)在任务偏好下是否可以成功,主要因为(Cl,Vl)内部存在如下情形:

1)如果∃aj ∈Cl中,Tj ∩Vl=∅,这意味着aj对Vl根本不感兴趣,此时(Cl,Vl)不可能成功;

2)即使情形1)满足要求,如果∃ti ∈Vl,对∀aj ∈Cl,ti∋Tj,即Cl中没有一个成员对ti感兴趣,此时(Cl,Vl)也不可能成功;

3)即使情形1)–2)均满足要求,如果∃ti ∈Vl,∃k ∈,即Cl中所有对ti感兴趣的智能体拥有的资源总量不可能满足ti的需求,则(Cl,Vl)也不可能成功;

4)即使情形1)–3)均满足要求,如果不同任务对同一智能体的资源需求超过了该智能体的负荷,即因为不同任务的竞争而产生资源冲突,则找不到一个可行的资源分配方案让Vl中的所有任务都同时满足,此时(Cl,Vl)也不可能成功.

显而易见,上述4种情形中,前面3种情形很容易基于(Cl,Vl)进行判定,如算法1所示(算法1见表2).如果经过算法1检查后,(Cl,Vl)是有效的,需要进一步检查(Cl,Vl)是否存在潜在的、不可见的资源冲突,这将最终决定(Cl,Vl)是否成功.为此,一个棘手的问题摆在本文面前: 如何检查(Cl,Vl)以发现潜在的资源冲突?

表2 算法1 (Cl,Vl)的成员有效性判别Table 2 Algorithm 1 Feasibility checking of the members in(Cl,Vl)

表3 算法2 孤立联盟(Cl,Vl)的成功性判别Table 3 Algorithm 2 Succcess checking of the non-overlappin coalition(Cl,Vl)

表4 算法3 关联联盟集的成功性判别Table 4 Algorithm 3 Succcess checking of SIOC

为了解决这个问题,本文基于(Cl,Vl)构造一个如图2所示的流网络.具体来说,首先在有向图中添加一个源点和一个汇点.Cl中的每个智能体成员aj都是源点附近的供应节点,在源点和每个aj之间都有一条弧,弧上的容量值为aj持有的第k维资源量.Vl中的每个任务ti都是汇点旁边的一个需求节点,在汇点和每个ti之间也有一条弧,弧上的容量值为ti对第k维资源的需求量.对于∀aj ∈Cl和∀ti ∈Vl,只要ti ∈Tj,即aj对ti感兴趣,aj和ti之间就会存在一条弧,弧上的容量值为aj在第k维资源上能够为ti贡献的最大值,即min.

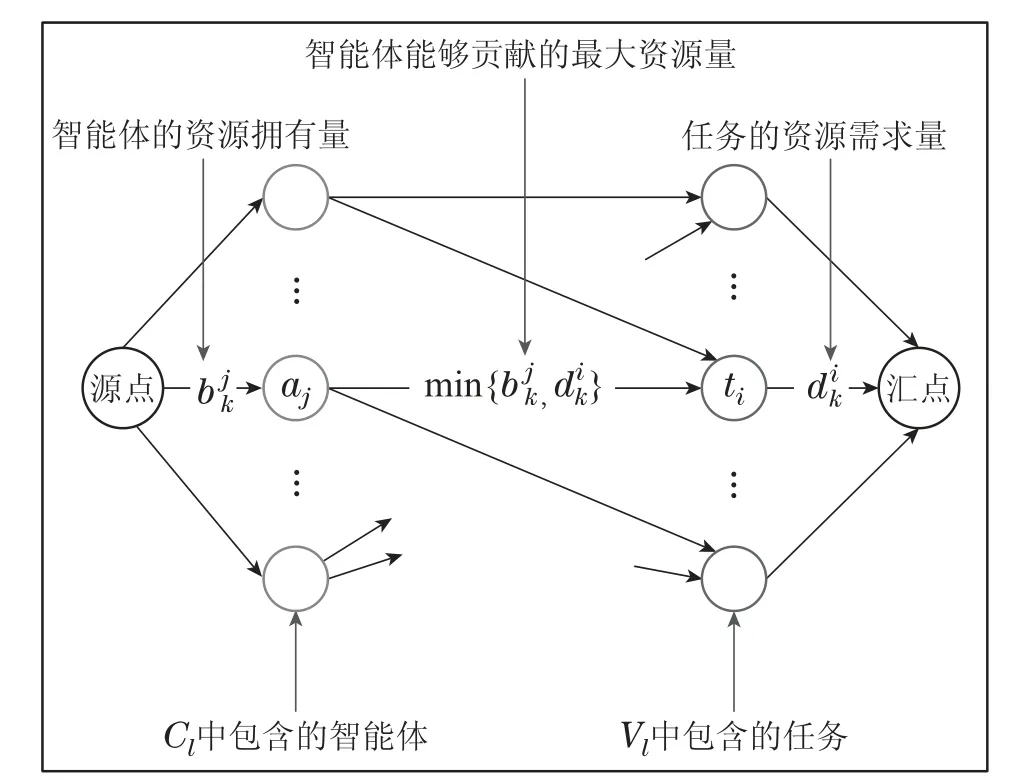
图2 基于(Cl,Vl)构造的流网络Fig.2 Flow network construction based on(Cl,Vl)

构造好上述的流网络,本文可以使用经典的Edmonds-Karp算法[13]计算网络中的最大流.根据最大流最小割定理,如果网络中的最大流小于,则网络中不可能存在一个可行流使得汇点到ti之间的每条弧都饱和.这意味着,Vl中的多任务之间在第k维资源上存在着激烈的资源冲突,根本找不到一个可行的资源分配方案使得Vl满足.如果网络中的最大流大于或等于,则这个最大流即是一个可行的资源分配方案使得Vl中的每个任务在第k维资源上都能被满足,且没有任何资源冲突.

命题9算法2的时间复杂度至多为O(n6).

证首先,Cl中至多有n个智能体,Vl中至多有m个任务.因此,判断(Cl,Vl)中智能体和任务有效性的时间复杂度至多为O(n+m).其次,对Vl中的每一个ti,本文需要判断每一维资源是否能被满足,其时间复杂度至多为O(m×r).此外,计算最大流的Edmonds-Karp算法其时间复杂度为O(ν×ε2)[13],其中ν和ε分别是网络中的节点数和弧数.从图2中可以看到,网络中最多有(2+n+m)个节点和(n+n×m+m)条弧,又每一维资源都需要通过流网络进行评估,故其时间复杂度至多为O(r×(n+m)×(n+n×m+m)2).综上,算法1的时间复杂度至多为O(n+n2+n6)=O(n6),具有多项式复杂度,这与命题6的结果一致.证毕.

4.2 重叠联盟的成功性判别

给定一个重叠联盟(Cl,Vl),不仅需要检查其内部是否是有效的,即需要检查第4.1节的情形1)–4),还需要检查与(Cl,Vl)交叉成员相关联的其他重叠联盟的有效性,以及这些重叠联盟之间是否存在资源冲突问题.为此,本文将与(Cl,Vl)相关联的所有重叠联盟放在一起综合考虑.例如,OCS={({a1,a2},{t1}),({a2,a3},{t2}),({a3,a4},{t3})},对重叠联盟{({a1,a2},{t1})来说,与之关联的其他联盟有({a2,a3},{t2}),而({a2,a3},{t2})又与({a3,a4},{t3})关联.因此,需要把这3个联盟放在一起考虑,构成一个关联联盟集(set of involved overlapping coalitions,SIOC).

本文首先基于算法1依次对这些重叠联盟进行有效性检查,只要有一个联盟是无效的,则将该联盟从SIOC中剔除.如果最后的SIOC=∅,则这些关联的重叠联盟均不可能成功.如果检查过后的SIOC∅,则再基于SIOC 构造一个流网络,如图3所示.与图2不同的是,这里智能体aj和任务ti之间存在一条弧,当且仅当aj和ti属于同一个重叠联盟,且aj对ti感兴趣.也就是说,智能体aj和任务ti之间的弧是根据每个重叠联盟来划分的.如果ti和aj不在同一个联盟里面,即使aj对ti感兴趣,也不能构造一条弧,因为SIOC里面根本不存在这样的协作.

图3 基于关联联盟集构造的流网络Fig.3 Flow network construction based on SIOC

命题10算法3的时间复杂度至多为O(n7).

证由命题9可知,算法3的主要耗时在于最大流计算,其时间复杂度至多为O(n6).此外,由命题1可知,SIOC中至多有m个集体任务集非空的重叠联盟.因此,算法3 的时间复杂度至多为O(m×n6)=O(n7),也是多项式复杂度,与命题6的结果也是一致的.证毕.

4.3 OCS的成功性判别

基于算法2和算法3,本文提出一种OCS成功性判别算法,如算法4所示(算法4见表5).具体来说,对于待评估的一个OCS,首先对OCS进行遍历,划分出所有的孤立联盟和关联联盟集.对于每个孤立联盟,调用算法2进行判别;对于每一个关联联盟集,调用算法3进行判别.然后对于所有判定成功的联盟,基于式(1)–(2)计算联盟结构值.需要注意的是,关联联盟集可能不止一个.

表5 算法4 OCS成功性判别Table 5 Algorithm 4 Succcess checking of OCS

命题11算法4的时间复杂度至多为O(n7).

证在算法4中,对孤立联盟和关联联盟集的判别占据了主要的计算开销.根据命题9和命题10可知,其时间复杂度分别至多为O(n6)和O(n7).因此,算法4的时间复杂度至多为O(n7),也是多项式复杂度,与命题7的结果一致.证毕.

4.4 最优OCS生成

利用算法4,就可以基于穷举法,通过遍历所有可能的OCS,寻找最优重叠联盟结构OCS∗,如算法5所示(算法5见表6).

表6 算法5 最优OCS生成Table 6 Algorithm 5 Optimal OCS generation

命题12算法5 的时间复杂度至多为O(7).

证由命题11可知,算法4的时间复杂度至多为O(n7).在算法5中,要想找到最优联盟结构OCS∗,需要遍历所有可能的重叠联盟结构,而总共可能的重叠联盟结构数为.因此,算法5的时间复杂度至多为O(7).又根据命题5可知,至少是指数级的,可知算法5的时间复杂度至少是指数级的,这与命题8的结果一致.证毕.

5 仿真实验

由命题8和命题12可知,搜索最优重叠联盟结构是多项式时间难解的,只有在智能体数和任务数很小的情况下才是可行的,为了验证这一猜测,在本节,本文基于不同的参数来测试算法5.这些参数选自笔者前期的数据集[7,14].每组参数在Intel Xeon CPU2.2 GHz、内存32 GB、操作系统Windows Server 2012的个人计算机上独立运行30次.

需要指出的是,当n=5,m=5时,根据命题5,可能的重叠联盟结构总数将近225≈108.经过测试,此时保存这些重叠联盟结构需要耗费的内存达到了10.3 GB左右,导致算法5无法正常执行.因此,在下面的测试中,以n=3,r=5,1 ≤m≤5和m=3,r=5,1 ≤n≤5 的参数设置进行仿真实验,以验证搜索最优重叠联盟结构的时间消耗是否与智能体数和任务数呈指数关系.

图4 给出了算法5 在不同n或m下占用的内存(均值,字节).由图4可以看出,当m=3,r=5,1 ≤n≤5时,随着智能体数的增加,算法5占用的内存缓慢增长,到n=5 时剧烈增加,增加了2.5 倍多.当n=3,r=5,1 ≤m≤5时,随着任务数的增加,算法5占用的内存也是增长缓慢,但在n=5时陡然增加,增加了3.5倍多.上述实验结果表明,算法5的解空间随着n,m的增加至少是指数级的,与命题5的分析结果一致.

图4 不同n或m下算法5占用的内存(均值,字节)Fig.4 Consumed memory (mean,in bytes) of Algorithm 5 under different numbers of agents and tasks

图5给出了算法5在不同n或m下耗费的时间(均值,s).由图5可以看出,当m=3,r=5,1 ≤n≤5时,随着智能体数的增加,算法5耗费的时间缓慢增长,到n=5时剧烈增加,增加了近4 倍.当n=3,r=5,1 ≤m≤5 时,随着任务数的增加,算法5耗费的时间也是增长缓慢,但在n=5时陡然增加,增加了8倍多.上述实验结果表明,算法5耗费的时间随着n,m的增加至少呈指数级增长,与命题8和命题12的分析结果一致.

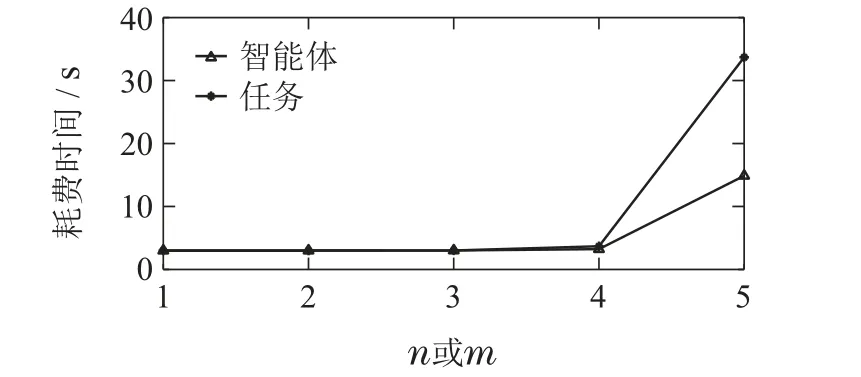
图5 不同n或m下算法5占用的时间(均值,s)Fig.5 Consumed time (mean,s) of Algorithm 5 under different numbers of agents and tasks

6 与已有模型的对比分析

在本节,本文讨论几个与本文面向任务的OSG模型类似的几个联盟博弈模型,并分析之间的异同.

传统的联盟结构生成博弈[4]旨在寻找智能体集合的一个最优划分,以使联盟结构值最大化.不过,每个联盟的效用是已知的,与任务无关.因此,联盟结构生成博弈只具有理论上的价值,难以应用实际.

技能结盟博弈[5]是不确定环境中一个联盟协作模型,其中每个智能体都有一组完成各种任务所需的技能,每个任务都需要一组技能才能完成,但每个技能都很难量化,只能定性的表达.

在资源结盟博弈[6–7]中,每个智能体都有自己的兴趣集,并且只有当智能体在联盟的协作任务集中发现一个其感兴趣的目标时,才会加入该联盟.但是,一旦智能体加入该联盟,它就可以向协作任务集中的所有任务提供资源,哪怕对这个任务根本不感兴趣.此外,只有当协作任务集能够激励联盟中的每个成员,同时联盟拥有足够的资源来实现协作任务集中的所有任务时,联盟才被认为是成功的.Su等[7]约定每个智能体只能对其感兴趣的任务贡献资源,并分析了这种苛刻条件下的单个联盟成功性条件和计算复杂性,但没有涉及联盟结构模型的分析.

传统OCFGs允许每个智能体都可以参与任何联盟,响应任何任务,只要其拥有足够多的资源.在这种情况下,OCS是智能体集合的一个覆盖,而不是划分.Chalkiadakis等[15]首先探讨了OCFGs的核及其稳定性问题.Zick等[8–9]提出了一种仲裁OCFGs模型,并讨论了仲裁核的稳定性,还证明了仲裁OCFGs中许多决策问题的计算复杂性在很大程度上取决于每个智能体拥有的资源量和联盟规模.Mamakos 和Chalkiadakis[16–17]提出了一种迭代OCFGs,其中每个智能体都不知道其他智能体拥有的资源量,但对其他智能体的潜在资源投资具有一个贝叶斯信念.魏冰茹等[18]考虑智能体的资源具有成本代价,基于动态规划求解总成本最小的OCS.郭志鹏和刘惊雷[19]通过限制联盟数和计算联盟结构相似度设计了一种联盟约束贪心算法.桂海霞等[20]和Zhang等[14]将进化算法与启发式搜索相结合,可以为给定的批量任务快速生成近似最优OCS.

与上述联盟模型,尤其是与传统OCFGs不同的是,本文聚焦面向任务的重叠联盟形成,规定每个智能体都只有有限的资源,且只能对任务集中的部分子任务做出响应,OCS中的每个联盟只能承担相互不相交的任务子集,即不允许任务重复执行.此外,每个联盟是智能体子集和任务子集的一个二元组合,所有的智能体子集构成所有智能体的一个覆盖,而不是传统的划分,所有的任务子集构成所有任务的一个划分子集,旨在根据当前有限的智能体资源,选择一个最佳OCS来完成给定任务集中最有利可图的子集.

7 结论

在面向任务的环境下,如何判别联盟结构的成功性成为一个难点.为此,本文首先构建了一种新的面向任务的最优重叠联盟结构生成问题模型,给出了成功联盟和成功联盟结构的相关定义,并分析了其解空间和计算复杂性.本文还基于流网络分别设计了相应的孤立联盟、重叠联盟、重叠联盟结构成功性判别算法和最优重叠联盟结构搜索算法,并进行了仿真实验.结果表明,搜索最优重叠联盟结构需要占用巨大的内存和计算开销,难以满足实际应用.因此,在下一步研究工作中,本文将重点研究如何基于元启发式算法在可接受的存储和计算开销内快速搜索到近似最优重叠联盟结构.