基于副边解耦极板的电容式无线电能传输系统拾取端失谐评估

周 玮，郑宇锋，陈泽林，李志强，易云天，麦瑞坤

（西南交通大学电气工程学院，四川省 成都市 611756）

0 引言

电容式无线电能传输（capacitive wireless power transfer，CWPT）技术是一种利用金属极板间的电场作为传输介质的无线电能传输（wireless power transfer，WPT）技术［1-3］。作为WPT 技术的重要形式，CWPT 系统具有诸如小型化、重量轻、形状灵活和涡流损耗低的特性［4-5］。近年来，学者们将CWPT 技术的应用场景拓展到生物植入设备［6］、水下设备［7］、电动汽车［8-9］以及轨道交通等方面［10-11］。

日趋复杂的应用场景，也对WPT 系统的稳定性提出了更高的要求。然而，原副边耦合机构偏位、元件参数误差和温漂效应等都将引起系统失谐，导致系统输出功率波动、传输效率下降［12-14］。此外，由于CWPT 系统工作频率较高，致使整流器输入阻抗的虚部值不能够再被忽略，且该阻抗虚部值受负载与整流器直流侧电压的影响而变化，这将给CWPT系统的谐振稳定带来挑战［15-16］。

为确保CWPT 系统在参数变化时能够及时调整恢复至谐振状态，必须对系统的失谐程度进行评估。对于系统发射端回路来说，在保持拾取端回路谐振的前提下，存在多种失谐评估方式，且评估所需的电参量均可被直接观测得到。然而，对于系统拾取端回路来说，由于拾取端的感应电压难以被直接观测到，故无法简单地通过测量感应电压和拾取端回路电流的相位差来评估拾取端回路的失谐程度。综上所述，拾取端回路失谐程度的评估是判断CWPT 系统谐振状态的前提和难点。

当前，国内外关于CWPT 系统失谐程度评估的研究较少。由于电感式无线电能传输（inductive wireless power transfer，IWPT）技术与CWPT 技术具有对偶性［17］，关于IWPT 系统失谐程度的评估方法对CWPT 系统同样具有参考意义。文献［18］提出一种基于负载电流的系统谐振评估方法，该方法通过调节系统工作频率来保持发射端谐振，进而检测负载电流来判断拾取端回路的谐振状态。然而，该方法仅能得知回路是否失谐，无法对失谐程度进行评估。文献［19］提出一种系统感性参数识别的方法，该方法仅依靠采样电压和采样电流的有效值实现。然而，由于该方法要求每次在系统失谐评估前先断开拾取端回路，无法适用于需要对参数进行实时检测的场景。文献［20］针对IWPT 系统提出一种基于原边解耦线圈的拾取端电流检测方法，类似的方法也应用于双向IWPT 系统的原副边信号同步中［21］。但该方法难以适用于CWPT 系统，一方面是由于目前关于电容式解耦型耦合机构的研究较少，另一方面是由于CWPT 系统的特性，整流器输入阻抗的虚部值将对拾取端失谐程度的评估造成干扰。

综上，本文针对拾取端回路的失谐程度评估，分析并提出了一种间接测量拾取端感应电压、评估拾取端回路失谐程度的CWPT 系统。本文主要创新点如下：1）针对CWPT 系统的拾取端感应电压，提出一种间接观测其相位信息的副边解耦型耦合机构；2）在考虑理想模型误差和测量误差的情况下，提出拾取端回路失谐程度的评估校正方法。依据系统建模与分析、副边解耦型电容式耦合机构分析、检测电路与误差校正，最终搭建了带有副边解耦极板的CWPT 系统原理样机，验证本文的设计与分析。

1 系统建模与分析

如图1 所示，本文提出的CWPT 系统由直流电源、逆变器、补偿网络、耦合机构、整流器、负载和检测校正系统几部分共同构成。图中：耦合机构为三端口网络，端口电压分别为U̇1、U̇2和U̇3，端口电流分别为İ1、İ2和İ3。极板P1、P2与外接电容Cex1组成发射端；极板P3、P4与外接电容Cex2组成拾取端；极板P5、P6与外接电容Cex3组成检测端。系统检测端保持开路，发射端采用由电感L1a、L1b及电容C1组成的LCL 补偿网络，拾取端采用由补偿电感L2组成的串联补偿网络。负载电阻为RL，系统的输入电压为Edc，输出电压与电流分别为UR和IR。

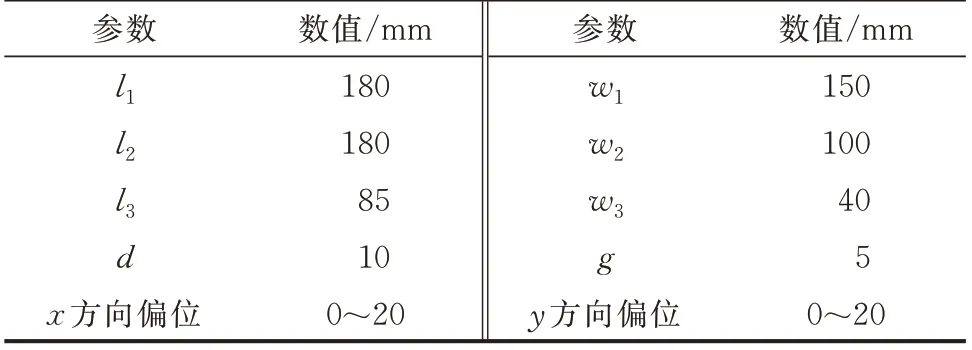
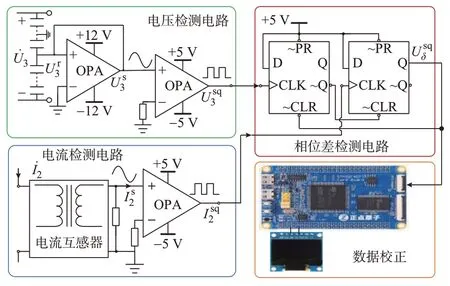
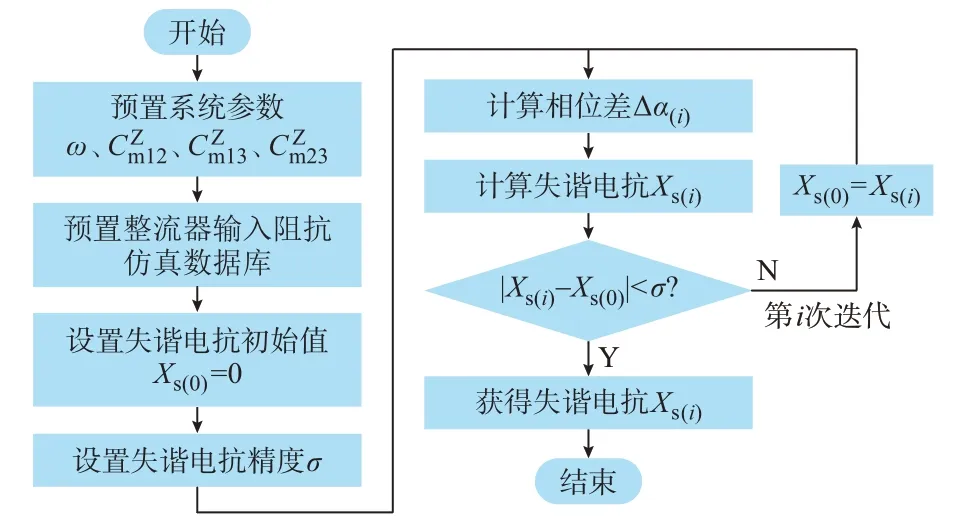
考虑每两个极板间均存在耦合电容，用Cij表示（1≤i

根据文献［22］中所描述的基于Z 参数的多端口电容式耦合机构的一般电容模型，对本耦合机构进行建模，利用耦合电容参数Cij，可得各端口电压、电流关系如式（1）所示。

式中：ω为角速度；和分别为发射端、拾取端和检测端的端口自电容；和分别为“发射端-拾取端”“发射端-检测端”和“拾取端-检测端”的端口间互电容。检测端由于保持开路，则电流İ3=0。

根据式（1）可得耦合机构的端口电压表达式如下：

即端口i的端口电压U̇i可视为由两部分组成，第1部分为回路电流İi流经自电容所形成的电压，第2 部分为其余端口回路电流İj基于互电容在端口i上产生的感应电压（i，j≤3）。定义端口i上由回路电流İj产生的感应电压为：

即端口i与端口j的互电容值越大，由此产生的感应电压U̇ij则越小，耦合强度越弱，即端口间的耦合强度与其基于Z 参数的互电容值成负相关。

由式（1）—式（3）可得本CWPT 系统的简化等效电路如附录A 图A1 所示。图中：Uinv为逆变器等效交流电源；Zrec为整流器等效输入阻抗。补偿电感L1a、L1b、L2与电容C1以及端口自电容的谐振关系为：

依据回路阻抗关系可知，在拾取端回路中，感应电压U̇21与回路电流İ2间的相位差能够用以反映拾取极板所在回路的失谐程度。当拾取端为串联补偿拓扑时，U̇21与İ2间的相位差所反映的失谐程度即为系统拾取端的失谐程度；若拾取端采用LCL 等高阶补偿拓扑，则U̇21与İ2间的相位差仍可判定拾取极板所在回路的谐振状态，这一功能与CWPT 系统原副边的补偿拓扑无关。然而，受端口自电容CZ2的影响，端口电压U̇2并不能准确表达感应电压U̇21的相位信息，故仅依靠直接观测得的电参量难以实现对回路失谐程度的评估。同时，观察检测端的端口电压U̇3可得：

故式（5）可以改写为：

对比U̇21的表达式和式（7）可发现，此时U̇21与U̇3具有相同的相位，均相比于İ1滞后π/2，故可以通过检测端口电压U̇3间接获得拾取端感应电压U̇21的相位信息。进而，利用电压U̇3与电流İ2之间的相位差来判断系统拾取端谐振状态。定义端口电压U̇3与回路电流İ2的相位差为φ，则有：

理想情况下，整流器等效输入阻抗为纯电阻Rrec：

对系统拾取端回路的阻抗关系及电压、电流相位关系分析详见附录A 图A2。图中：Xs为拾取端回路的失谐电抗，可见失谐电抗Xs与整流器输入电阻Rrec的阻抗角即为电压U̇3与电流İ2的相位差φ。从而，可推导得到拾取端回路电抗jXs如式（10）所示。

通过对失谐电抗的计算，能获知CWPT 系统拾取端回路的失谐性质及与回路失谐程度。因此，可将失谐电抗jXs作为CWPT 系统拾取端回路失谐程度的评估标尺。

2 副边解耦型电容式耦合机构

同时，为保证检测端极板始终与发射端极板保持耦合，设计发射端极板由一对“L”型极板P1、P2以互补形式拼接置于系统原边，如图2（a）所示；发射端极板纵向部分分别正对于拾取端极板P3、P4，横向延伸出的部分则分别正对于检测端极板P5、P6，如图2（b）所示。各极板的具体尺寸参数如表1 所示。表中：w1、w2、w3分别为发射端、拾取端、检测端极板的宽度。

表1 耦合机构尺寸参数Table 1 Geometric dimension parameters of coupler

图2 副边解耦型电容式耦合机构Fig.2 Structure of secondary-side decoupled capacitive coupler

基于ANSYS Maxwell 搭建耦合机构模型并进行仿真分析，得到不同偏位方向、各端口间的互电容值随副边极板偏位增加的变化曲线，如附录A 图A4所示。

综上所述，本文所提出的耦合机构在一定偏位范围内，能够满足副边极板的解耦需求，实现对拾取端感应电压的获取，并且该偏位范围受检测端极板的尺寸限制。

3 检测电路与误差校正

3.1 检测电路

由于当前电压和电流霍尔元件的带宽均小于500 kHz，在CWPT 系统较高的工作频率下难以实现对信号的完整采样。为完整采集检测端电压U̇3与回路电流İ2，以准确得到其相位差，本文设计检测电路共包含电压检测、电流检测、相位差检测三部分，如图3 所示。图中：OPA 为运算放大器；CLK 为时钟；PR 为复位；～表示取非，当输入信号为低压时，引脚功能起作用，否则只在高压时起作用。首先，对于电压检测电路，先将多个容值相等的分电容串联组成电容阵列，再并联在检测端作为补偿电容Cex3。随后，将电压跟随电路的输入端反并联在其中一个分电容的两端，以获取与检测端电压U̇3反相的信号，利用电压跟随电路对反相信号进行采样，得到采样信号。同时，利用电压跟随电路输入阻抗无穷大的特性，可减小后级检测电路对分电容容值的干扰。进而，将采样信号传输至过零比较电路，并转换为对应的方波信号。类似地，在电流检测电路中，利用电流互感器对拾取端电流İ2进行采样，获得电流采样信号，并传输至过零比较电路进一步转换为相位相同的方波信号。由此，各电压、电流信号的相位关系变换如附录A 图A5所示。

图3 失谐程度检测电路Fig.3 Detection circuit of detuning state

相位差检测电路则由两个D 触发器构成，输出占空比为δ的方波信号，其受电流方波信号的上升沿触发开始和电压方波信号的上升沿触发结束，故可由该方波信号的占空比δ得到端口电压U̇3与回路电流İ2的相位关系。由附录A 图A5 可知，在理想情况下，若端口电压U̇3与回路电流İ2同相位，即拾取端回路处于谐振状态，则占空比δ=50%；若端口电压U̇3滞后于回路电流İ2，即拾取端回路呈容性失谐，则50%<δ<75%；若端口电压U̇3超前于回路电流İ2，即拾取端回路呈感性失谐，则25%<δ<50%。故可推导得到电压U̇3与电流İ2的相位差φ为：

当拾取端回路呈容性失谐时，-π/2<φ<0；当拾取端回路呈感性失谐时，0<φ<π/2。

3.2 误差校正

为使得检测、评估的结果更接近系统运行的真实情况，需考虑系统在实际工作中与理想情况下的误差，主要包括：整流器等效输入阻抗误差、检测端电压U̇3和拾取端感应电压U̇21间的相位差以及采样电路的滞后误差。其具体分析如下：

1）整流器输入阻抗误差。由于系统工作在较高的频率下，全桥整流器的输入阻抗不再为纯电阻，其虚部值不再能够忽略且大小受二极管参数、负载电阻和整流器直流侧电压的影响。整流器输入阻抗的实际值难以测量或简单通过整流器输入、输出电压、电流推算得到。

利用Advanced Design System 仿真软件，搭建基于SiC 二极管SCS310 的全桥整流器模型，并在负载RL为50～100 Ω、直流侧电压UR为10～50 V 条件下进行仿真，得到整流器等效输入阻抗中的实部值和虚部值如附录A 图A6 所示。仿真结果表明，在500 kHz 的工作频率下，全桥整流器等效输入阻抗的虚部为负值，并且比较发现该虚部值与实部值具有相同数量级，同时实部值也不满足式（9）所示的理论计算值。因此，设高频条件下该全桥整流器等效输入阻抗为：

2）电压U̇3和U̇21的相位误差。由式（5）可知，当拾取端极板与检测端极板解耦非理想时，感应电压U̇32将造成端口电压U̇3与感应电压U̇21间存在相位误差Δα，其具体相位关系如附录A 图A7 所示。以电流İ1相位为基准，α21为电压U̇21的相位角，α31为电压U̇3的相位角。

根据拾取端回路阻抗关系和式（3）、式（10），可得拾取端电流İ2为：

将式（13）代入式（5）可得：

定义端口电压U̇3与电流间İ1的等效阻抗为：

可得端口电压U̇3与感应电压U̇21间的相位差Δα为：

由式（15）和式（16）可知，当耦合机构尺寸参数确定后，其互电容也随之固定。因此，端口电压U̇3与感应电压U̇21间的相位差Δα可通过Zrec的仿真值和jXs的测量值计算得出。然而，在系统初始工作时，尚未完成对jXs的第1 次测量，故可在控制器中设失谐电抗的初值jXs（0）=0，计算得此时相位误差Δα（0），并对检测电路所得测量值进行补偿，由此计算得失谐电抗的测量值jXs（i），进而继续将jXs（i）代回式（15）和式（16）计算得相位误差Δα（i），最终通过多次迭代计算将失谐电抗的测量值误差限制在预设精度之内。该迭代计算流程具体如图4 所示。

图4 相位差误差迭代校正流程图Fig.4 Flow chart of iterative correction of phase difference error

3）采样电路滞后。如附录A 图A8 所示，检测端电压U̇3经过采样并转换为方波信号的过程中，信号从元器件输入到输出间存在滞后。该滞后时间仅与元器件的外围电路参数和元器件工作环境温度有关，其具体数值可从相应元器件数据手册中获知。设电压采样和转换的滞后时间分别为和；类似地，方波信号也滞后于电流İ2，设电流采样和转换的滞后时间分别为和。

由于采样方式、所用器件的不同，电压、电流的采样滞后时间也不相同，设对方波信号造成的占空比误差为Δδ，则

式中：T为系统工作周期。

综上所述，经校正后拾取端回路失谐电抗jX*s的表达式可由式（10）修改为：

4 实验分析

4.1 实验样机

由于整流器输入阻抗的实际值和系统拾取端失谐电抗实际值难以测量得到，为验证所提出的系统拾取端失谐评估方法的有效性和准确性，设计实验系统如附录A 图A9 所示。先将拾取端回路调整至谐振状态，再在拾取端串联已知感值的电感或已知容值的电容，以分别模拟拾取端回路谐振、感性失谐和容性失谐3 种谐振状态。

根据所设计的CWPT 系统搭建实验样机，如附录A 图A10 所示。利用印刷在印制电路板（printed circuit board，PCB）上的铜箔作为耦合机构的极板，并能确保同侧极板保持在同一平面上。利用高压陶瓷电容作为发射端和拾取端的外接电容Cex1、Cex2。检测端的外接电容Cex3则由薄膜电容串并联阵列构成，以便对端口电压U̇3实现分压，达到检测电路的输入电压范围。补偿电容C1也由薄膜电容组构成。补偿电感由Litz 线缠绕在高频硅铁磁芯上构成，高频磁芯有利于提高电感的功率密度并减少Litz 线材的用量，有利于减小补偿电感的体积，同时，也能够减小电感电磁辐射和电感的参数敏感性。系统各参数值如表2 所示。表中：f为频率；Ct为谐振电容。

表2 系统样机的各项电路参数Table 2 Circuit parameters of system prototype

利用数字信号处理（digital signal processing，DSP）芯片产生频率为500 kHz 的脉冲调制控制信号，对逆变器进行控制。逆变器MOSFET 管的型号为C2M0080120D，整流器的SiC 二极管型号为SCS310。负载为滑动变阻器，便于实现不同负载值的调节。

检测电路中，电压跟随器所用为OPA2810 双电源、轨到轨运算放大器；电流霍尔元件采用的是侵入式电流互感器PA1005；过零比较电路中比较器的型号为TLV3501；而作为相位差检测的D 触发器型号为74AC11074；最后，利用控制器STM32F403 对检测数据进行处理。

4.2 相位差检测验证

当系统工作频率为500 kHz、负载RL=70 Ω、负载两端电压UR=30 V 时，在拾取端回路分别处于谐振、感性失谐、容性失谐3 种谐振状态，测得发射端回路电流İ1、拾取端回路电流İ2、端口电压U̇3和相位差占空比δ的波形，如附录A 图A11 所示。

从图中可以看出，在拾取端回路谐振、感性失谐和容性失谐时，电压U̇3的相角α31分别为-88.2°、-86.7°和-87.1°，相比于前文所分析的相比于İ1滞后π/2 的理论值，可知此时端口电压U̇3与感应电压U̇21的实际相位误差分别为1.8°、3.3°和2.9°。

同时，由附录A 图A11（a）中可看出，在拾取端谐振，回路无串联外电抗时，电压U̇3仍滞后于电流İ2，可推得此时拾取端回路呈容性失谐，与前文整流器等效输入电抗为负值的仿真结果分析相符合。

此外，由附录A 图A11 可观测得在拾取端回路不同谐振状态下，端口电压U̇3与回路电流İ2的相位差实际值分别为-9.56°、18.4°和-33.7°，而检测电路测得的相位差占空比δ分别为53.45%、45.59%和60.52%，代入式（11）可计算得检测电路所测得相位差测量值分别为-12.42°、15.87°和-37.87°，进而可计算得相位差的测量值与实际值误差分别为2.86°、2.53°和4.17°。这证明可通过检测电路较为准确地判别拾取端回路的谐振状态，并在一定程度上反映出系统电压U̇3与电流İ2的相位差φ。

4.3 系统失谐评估

图5 不同失谐情况下的拾取侧串联电抗的评估值Fig.5 Estimation value of series reactance at pickup loop under different detuning conditions

5 结语

本文提出了一种间接测量拾取端感应电压的三端口CWPT 系统。基于Z 参数建立了多端口电容式耦合机构的数学模型和等效电路，给出满足感应电压间接测量的副边极板耦合条件和拾取端失谐程度的评估模型。基于耦合条件，提出一种副边解耦型电容式耦合机构，并针对该耦合机构设计检测电路。在考虑理想模型误差和测量误差情况下，提出了失谐程度的评估校正方法。

实验结果证明，本文提出的解耦型电容式耦合机构能够在不影响无线电能传输的情况下，实现对拾取端感应电压相位信息的间接检测。同时，完成对拾取端回路失谐程度的评估，实现当拾取端回路谐振时，失谐程度评估值与实际值误差不超过1 Ω；当拾取端回路感性失谐和容性失谐时，评估值与实际值误差分别低于2%和5%。本文所提方法仅针对耦合机构所在环路的失谐问题，下一步可对其他环路的失谐状态评估与调谐进行研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。