基于Gazebo 的深海网箱洗网机器人动力学仿真平台搭建
2024-03-06黄小华庞国良袁太平
邢 旺,黄小华 ,李 根 ,庞国良 ,袁太平
1. 浙江海洋大学,浙江 舟山 316022
2. 中国水产科学研究院南海水产研究所/农业农村部外海渔业可持续利用重点实验室/广东省网箱工程技术研究中心,广东 广州 510300
3. 三亚热带水产研究院,海南 三亚 572024
我国是海洋大国,发展海水养殖能充分发挥海域广阔的优势,满足人们对于优质水产动物蛋白的需求[1-2]。由于近海养殖日趋饱和,养殖压力不断攀升,资源和空间的问题日益加剧,因此人们将目光投向了具有水域面积辽阔、水质条件优良、水体交换速度快等优点[3]的深远海区域。
网箱是深海养殖中不可或缺的组成,大型深海网箱具有一般网箱没有的大容量、抗风浪和高效益等优点,同时大型深海网箱往往配备成套的智能系统,易实现无人值守和远程管控[4]。网衣清洗是深海网箱养殖必不可少的环节。网衣得不到及时清洁会影响鱼类生长,同时污损生物会增加网衣的重量,导致网衣、网箱的结构破坏风险增加[5-6]。
目前,网衣清洗可分为:人工清洗法、机械冲洗法和洗网机器人清洗法。人工清洗和机械清洗均费时费力,且会造成危险[7]。洗网机器人具有操作简单、安全便携和自动化程度高等优点。其主要由控制单元、运动单元和清洗单元等构成[8]。控制及运动单元解决机器人贴网移动、水下穿梭等问题,而清洗单元则可以通过多种不同的清洗工具达到对网箱网衣的清理。
总体上,在结构设计方面,研究者探索了各种不同的洗网方式,例如高压旋转水流、毛刷、空化射流等,旨在实现高效、便捷的网箱清洗。可分为清洗工具、清洗水流亦或两者综合使用。在清洗工具方面:通过清洗盘清洗喷嘴[9]或提供多种类型喷嘴的清洗单元来进行洗网作业[10],以及采用多个旋转刀片构成洗网清洁头实现高效清洗[11]等。在清洗水流方面:通过高压旋转水流[12]和通过空化射流进行清洗作业[13]。综合两者还有:采用水流和毛刷作为清洗方式[14]和通过清洗模块的形式进行清洗作业[15]等组合模式。
在运动控制方面,采用自动导航[16-17]、自适应抓钩控制[18]等控制策略,以实现洗网机器人的自主贴网移动。为应对深海环境中的复杂动力学,建立动力学模型、开展仿真研究也成为热点。基于视觉、声呐等各种传感器的控制方案也受到关注。
好的洗网机器人应具备水下抗扰动、低能耗的特点。然而洗网机器人在贴网移动、水下穿梭的过程中,受力复杂、非线性程度高、状态难以观测,要求大量、全面的实验数据来支撑控制器的优化,该方式成本高、耗时长。针对此问题,本文在物理仿真环境Gazebo 的基础上,设计并开发了一套洗网机器人动力学及运动学仿真平台,通过仿真来获得洗网机器人水下工作的完备数据,开展不同控制器的全面性能验证,助力洗网机器人的控制器开发及优化。
1 仿真平台架构
针对机械臂、无人驾驶等机器人仿真问题,研究者开发了多款机器人仿真软件,包括Webots、V-REP (现为CoppeliaSim)、MuJoCo 和Gazebo 等(图1),目前暂无针对水下机器人的仿真平台[19]。
本文选择Gazebo 作为基础仿真平台,主要原因是:1) 机器人操作系统ROS[20]提供了丰富的Gazebo 接口,因此Gazebo 方便联合ROS 开展机器人控制器开发;2) Gazebo 支持多种物理引擎,如ODE 和Bullet,且有直观、易操作的三维仿真界面 (图1-d);3) Gazebo 社区开源了UUV Simulator 项目,该项目可以支持搭建和测试水下机器人,仿真水动力对机器人的作用为本文的开发提供了参考[21]。
在Gazebo 和ROS 的基础上,本文设计了图2 所示的仿真系统架构。其中绿色部分为基础平台已经具备的功能,橙色部分为需要开发的功能。ROS 提供了良好的进程间通讯机制,针对机器人控制策略设计问题,需要开发状态估计模块、控制模块、日志记录模块等;Gazebo 提供了机器人建模语言及编译系统、3D 渲染功能及物理引擎,在此基础上,开发洗网机器人本体,并开发水动力、推进器、传感器等插件。本文针对的是动力学仿真问题,因此,主要介绍水动力插件和推进器插件相关内容。通过ROS-Gazebo 通讯接口,可实现两平台的信息交换[22]。
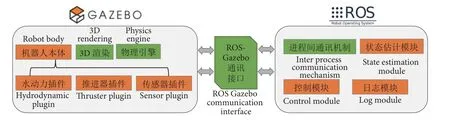
图2 仿真系统架构Fig. 2 Framework of simulation system
2 洗网机器人结构建模
结构对机器人动力学和控制性能有非常重要的影响。结构尺寸、外表面影响碰撞、摩擦、附加质量[23]等参数,推进器布置影响机器人的姿态控制,重心浮心位置影响机器人的稳定性,质量和惯量决定机器人的响应速度,上述因素综合影响着机器人的运动性能和操作能力。
构建洗网机器人本体结构步骤如下:1) 先在SolidWorks 软件中设计出机器人各零部件模型,包括机器人本体、推进器、洗盘3 个部分,并对零部件进行装配得到洗网机器人三维模型 (图3);2) 利用SolidWorks to URDF Exporter 插件设置机体、推进器和洗盘的坐标系、旋转轴以及父子关系;3) 获取机器人中各部件的相对位置关系和关节之间的关系,利用这些信息编写机器人模型xacro 文件;4)将各零部件导出为STL 格式用于描述机器人模型在Gazebo 中的外观元素部分;5) 设置机器人水动力模型参数,并将其数据编写软件包。
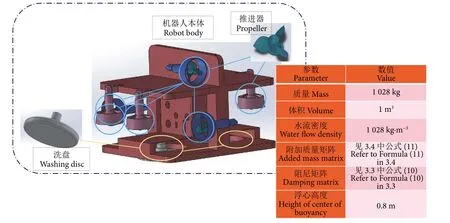
图3 洗网机器人本体结构图Fig. 3 Structure diagram of washing robot body
3 洗网机器人动力学建模
一旦洗网机器人的受力已知,就可模拟机器人在水下无输入情况下的运动轨迹,还可模拟机器人在控制作用下的运动轨迹,有助于深入理解洗网机器人的运动行为,设计及验证控制器性能[24]。
洗网机器人在工作过程中受力复杂,本文仅考虑影响较大的力,包括:浮力、重力、水阻尼力、附加质量效应、水流作用、推进器及洗盘作用。忽略了脐带缆、湍流、涡流等的影响[25],主要原因为:1) 考虑到机器人移动速度慢,设计时选用相对大功率的推进器,因此湍流、涡流对机器人的控制影响较小;2) 脐带缆在设计时会选用零浮力缆,在大部分场景下对机器人运动无影响 (少数情况的影响我们将在后续深入研究)。
本文依据Fossen 手册[26]海洋运载器的六自由度运动学方程建立洗网机器人动力学模型:
式中:v为洗网机器人速度向量,即机器人本体坐标系在世界坐标系下的速度在本体坐标系下的表示;v˙为洗网机器人加速度向量,即机器人本体坐标系在世界坐标系下的加速度在本体坐标系下的表示;η6×1为洗网机器人在世界坐标系下的姿态向量;M6×6=MRB+MA,为系统的惯性矩阵,MRB和MA分别为刚体和附加质量引起的惯性矩阵;C6×6=CRB(vr)+CA(vr),为系统的科里奥利向心矩阵 (下文简写为科氏力),CRB(vr)和CA(vr) 分别为刚体和附加质量导致的科里奥利向心矩阵;D6×6=DL+DN,为系统的阻尼矩阵,DL和DN分别为线性和非线性阻尼矩阵;g(η)6×1为系统的重力、浮力的合力矩矢量;g0为用于预调平 (压载控制) 的向量;τ∈R6×1,为推进器或其他动力元件产生的力和力矩;τb∈R6×1,为风、浪和流环境等不确定因素产生的干扰力。
下文将分别对公式 (1) 中出现的附加质量、科氏力、阻尼等作用力对机器人运动的影响进行仿真。需要注意的是,由于洗网机器人移动范围小且速度慢,因此地球旋转导致的科氏力可忽略,机器人旋转运动导致的科氏力由物理引擎自动处理,因此,下文不专门探讨科氏力对机器人的影响[27]。
3.1 推进器和洗盘
推进器通过螺旋桨旋转推水给机器人施加推力和转矩 (图4),推力和转矩与螺旋桨的转速、水流密度推力系数等相关,计算公式[28]为:

图4 螺旋桨洗盘对机器人施加的推力和转矩Fig. 4 Thrust and torque applied by propeller to robot
式中:τ为螺旋桨的推力;Q为螺旋桨的转矩;n为螺旋桨的转速;D为螺旋桨的直径;ρ为流体密度;KTp为螺旋桨的推力系数;KQ为转矩系数。
洗盘和推进器对机器人的作用类似,即提供一个推力和转矩,因此,采用和推进器一样的公式(2) 和(3),调整系数来获得洗盘对机器人的作用。只是动态特性时间常数需要减小,旋转系数需要增大。
3.2 重力和浮力
静止在水中的机器人,会受到重力和浮力作用。如果重心和浮心不重合,重力和浮力将产生恢复力矩,使得机器人姿态在平衡状态附近震荡[29]。水下机器人受到的浮力和重力如图5 所示,在NED 坐标系中,作用于浮心的浮力,作用于重心上的重力,重力与浮力组合作用可表示为:
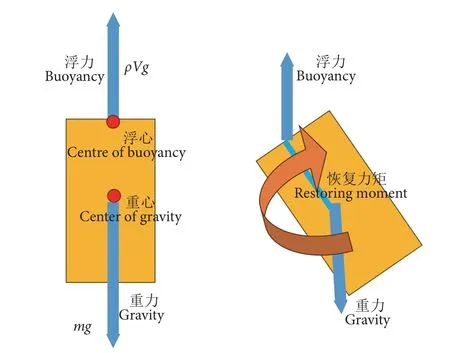
图5 重力、浮力共同作用示意图Fig. 5 Schematic diagram of combined action of gravity and buoyancy
式中:xg、yg、zg、xb、yb、zb分别表示重心和浮心在其坐标轴上相应的分量;B和W分别代表在z轴方向上的重力和浮力。
由于恢复效应为重心和浮心不重合所致,故z轴方向的旋转不受恢复效应影响,因此只考虑x和y轴方向波动所导致的转矩对机器人的影响。
在仅考虑重力和浮力的影响下,设置机器人重心 (0, 0, 0),浮心 (0, 0,zb),分别对机器人的x、y和z轴方向施加100 Nm 的冲击转矩,仿真机器人的运动轨迹 (图6)。

图6 Gazebo 中对机器人施加转矩 (以x 轴为例)Fig. 6 Applying torque to robots in Gazebo(Taking x-axis as an example)
由图7 可见,由于重力和浮力的恢复力距作用,机器人的x、y轴角速度作周期性的变化,而z轴角速度则保持在一个定值,这是因为浮力和重力方向均为竖直方向,无法在z轴方向上产生恢复力矩。
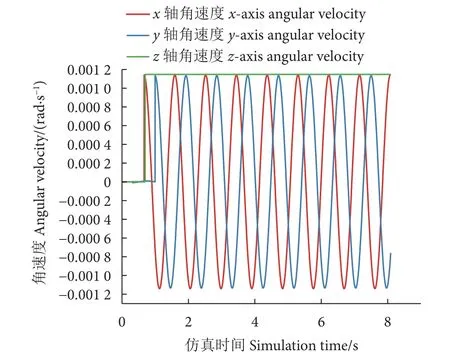
图7 重力、浮力作用下的角速度冲击响应Fig. 7 Angular velocity shock response under action of gravity and buoyancy
3.3 流体阻尼作用
机器人在水下运动会受到水流的碰撞和摩擦,导致阻尼作用,即速度越大,受到速度反方向的力就越大。阻尼作用可以建模为线性阻尼矩阵DL和非线性阻尼矩阵DN。
DL用于描述水动力引起的线性阻尼效应。该阻尼力矩阵是一个方阵,其元素表示不同自由度上的阻尼系数。它被用于分析水下机器人在运动过程中受到速度相关阻尼力的影响。线性阻尼力矩阵的规模和结构受水下机器人的几何形状、运动速度以及周围水流特性的影响 (图8)。其形式为:

图8 阻尼效应示意图Fig. 8 Schematic diagram of damping effect
式中:Xu、Yv、Zw、Kp、Mq和Nr为一阶阻尼系数。
DN用于描述水动力引起的非线性阻尼效应。该矩阵包含了一些非线性阻尼项,例如速度的高阶项和非线性耦合项。这些项反映了水下机器人在运动过程中非线性阻尼力的贡献,通常是由于机器人的非线性形变或流体动力学效应所引起的 (图8)。其形式为:
式中:Xu|u|、Yv|v|、Zw|w|、Kp|p|、Mq|q|、Nr|r|为二阶水动力系数。
两者结合即为阻尼矩阵D,表示为:
参考Berg[29]线性阻尼矩阵DL以及非线性阻尼矩阵DN可设置为:
组合两项作为其阻尼矩阵D为:
阻尼对机器人运动状态影响的仿真情况如下:
1) 阻尼对x、y、z轴方向平动线速度的影响。对x、y、z轴方向分别在0.5、0.2 及0.7 s 同时施加100 N 的单位冲击力,并绘制在同一幅图表上(图9-a)。可以观察到由于平动不涉及恢复效应,3 个方向均在单位冲击时达到最大线速度,并由于阻尼效应随时间减小;其中x、y轴方向的速度最终趋近于0,而z轴的速度并不为0,这是由于仿真过程重力略大于浮力,导致其在初始状态有一个初速度,并且最终在阻尼效应下速度回归于该初速度。

图9 阻尼效应对机器人平动和转动的影响Fig. 9 Effect of damping on translation and rotation of robots
2) 阻尼对x、y、z轴角速度的影响。对x和z轴在第0.8 秒时以及y轴在第1.25 秒时施加100 Nm 的单位冲击扭矩,并同时绘制在图9-b 上。可以观察到x和y轴的角速度变化规律完全相同。由于恢复效应的影响,它们均作周期性的阻尼震荡运动。且随着时间的增加,周期性幅度逐渐减小。而z轴方向由于不受恢复效应的影响,不会产生周期性的震荡,而是沿着光滑的凹曲线缓慢下降。
3.4 惯量及附加质量
附加质量的产生是由于机器人的移动带动周围流体运动状态变化而对机器人产生的反作用,用符号MA表示,其为6×6 的矩阵,包含36 个参数[30],由于机器人本体的对称性,本文将附加质量矩阵简化为对角矩阵,即附加质量不会改变机器人速度方向,只改变大小,设置:
根据欧拉力学[30],刚体质量和惯量对运动的影响可建模为MRB,即:
因此,惯量和质量共同作用下的影响矩阵为:M6×6=MRB+MA。讨论在惯量及附加质量共同影响下的仿真情况如下:
1) 无附加质量下x、y、z轴线性加速度的变化。为探究无附加质量对线性方向加速度的影响情况,分别对x、y、z轴施加100 N 的单位冲击力(图10-a)。除因仿真中误差导致的重力略大于浮力使得z轴的线性加速度略小于x和y轴外,其余加速度影响完全相同。

图10 单位冲击对有无附加质量线性加速度的影响Fig. 10 Influence of unit impact on linear acceleration with or without added mass
2) 有无附加质量对线性加速度的影响。经过分析仿真结果,在有附加质量时x、y、z轴的线性加速度变化完全相同,故只考虑有无附加质量对线性加速度的影响。以x轴作为观察附加质量对线性加速度影响的参考。对机器人施加公式 (11) 的附加质量矩阵,同时对其施加100 N 的冲击力。根据理论,在施加冲击力F不变的情况下,增加附加质量会导致其真实质量m增大,机器人的加速度a应该减小。但由于模拟仿真环境不像真实世界中时间为连续的变量,而是离散变量,故图10-b 中的反向加速度在真实时间中应和正向加速度同时发生,叠加之后的加速度a就比无附加质量时小,故其符合理论情况。
3.5 海流场力作用
海流是由海洋水体的流动引起的,具有一定的速度和方向。因此,机器人在海流中运动时,会受海流作用,产生阻力和推力[31]。考虑到水流对机器人的影响非常复杂,本文对该作用进行简化,即水流场的作用等效为在机器人质心处施加一个速度矢量,具体如图11 所示。
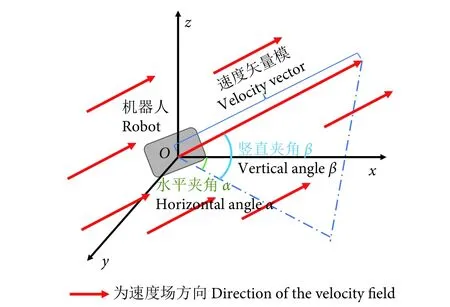
图11 流场图Fig. 11 Flow field diagram
其中与机器人前进方向x轴夹角也为水平夹角设为α,与xOy平面的夹角也为竖直夹角设为β。且其中的速度、水平夹角和竖直夹角如上图的参数。所以其各速度分量可以表示为:
式中:currentVel 为当前水流速度矢量,随着回调函数实时更新。
为增加仿真的真实性,引入噪声来模拟水下环境中的扰动。采用高斯马尔可夫过程 (Gauss-Markov process) 来模拟噪声的影响。通过引入噪声,能够更准确地模拟真实环境中的随机变动,从而提高仿真的真实性。高斯马尔可夫过程是一种常用于噪声建模和处理的数学模型[32]。它通常用来描述随机信号或噪声的变化过程,具有随机性、平稳性等特点。本模拟仿真使用下述公式来引入高斯噪声:
式中:var 表示当前时刻的过程状态或变量的值;step 表示时间步长;mu 表示过程的阻尼系数;noiseAmp 表示噪声幅值或强度;random 表示服从均匀分布的随机数,用来引入随机性或噪声成分,模拟真实世界中不确定的随机变动。
在不引入噪声的情况下,将速度矢量设为1 m·s−1,且与水平面和竖直面的夹角均为。观察线速度的变化曲线,海流场作用的仿真情况见图12。在3 s之前的图像满足模拟仿真结果。但3 s 之后出现了较大波动,这是因为机器人设置的深度为5 m,在波动时刻机器人冲出水面,然后在阻尼等的作用下出现波动并最终趋于稳定。
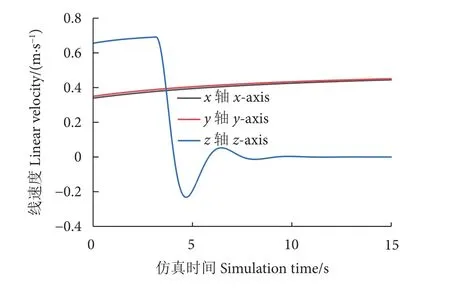
图12 无高斯噪声流场下的线速度零输入零状态响应Fig. 12 Linear velocity zero input zero state response in no gaussian noise flow field
将mu 设置为0.3,noiseAmp 设置为0.5,继续观察对机器人速度的影响情况。由图13 可见,噪声对线速度和角速度的影响非常大。如何通过控制策略来消除噪声对机器人平稳运行的影响是下一步要研究的问题,本文只涉及机器人模型的建立,未给出解决方案。
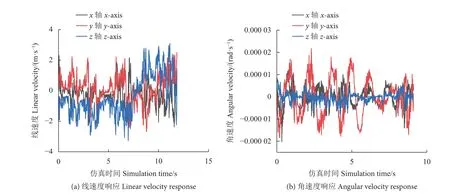
图13 流场高斯噪声下的线速度和角速度零输入零状态响应Fig. 13 Zero input and zero state response of linear velocity and angular velocity with Gaussian noise of flow field
3.6 网衣作用
洗网机器人在贴网移动时,会受到网衣的作用。网衣对机器人施加摩擦力、支持力,影响机器人在网面和垂直网面的运动。同时,网衣将网箱的移动作用到机器人上,改变机器人的状态;此外,网衣可能改变水动力特性,进而改变机器人的状态。在本文模拟仿真中,假设网箱固定,重点关注摩擦力和支持力的影响 (图14),忽略其他受力方面,这种简化有助于减少计算的复杂度。

图14 机器人在网箱表面的受力情况和贴网示意图Fig. 14 Force situation of robot on surface of cage and schematic diagram of sticking net
4 结论
本文基于Gazebo 仿真平台,搭建了洗网机器人仿真环境,实现了洗网机器人三维建模和动力学仿真。通过单元仿真的方式,分别建模或仿真了推进器及洗盘、流体阻尼、惯量及附加质量、海流场以及网衣对洗网机器人运动的影响。验证了仿真平台的有效性,为后续设计抗干扰能力强、能耗低的控制器奠定了基础。但目前的仿真平台中洗网机器人在水下的真实运动情况仍有提升的空间,体现在:1) 附加质量未考虑机器人的结构;2) 流场模型和现实有差别;3) 网衣作用缺乏有效模型;4) 未考虑推进器时滞效应;5) 未基于真实实验数据辨识机器人的受力情况。在后续的工作中将针对上述问题进行优化,尽可能地模拟洗网机器人在真实工况下的行为,为控制器设计提供数据支撑。
