基于经济成本目标的综合能源系统容量规划方法研究

2024-03-06李晓恩李泽鹏

煤炭工程 2024年2期

李晓恩，李泽鹏，周川，吴鹏，王雪

(国家电投集团科学技术研究院有限公司，北京 102209)

社会不断发展的同时也带来了能源短缺、环境污染等一系列棘手的问题，而日益增加的能源需求也对能源利用的合理性带来了严峻的挑战。综合能源系统(IES)能够协同规划多种能源，实现能量的耦合互补与能源的高效利用，因此被国际社会广泛关注[1，2]。

IES系统中设备容量的合理规划是系统高效平稳运行的重要保障，然而多种能源形式的耦合使得系统的规划及优化调度更加复杂[3，4]。文献[5]针对不同功能区的负荷特性，提出了考虑多功能区差异性的IES系统规划模型，显著提升了系统的经济性能。文献[6]在所建立的规划模型中考虑了配电线路和燃气管道的影响因素，以经济性为优化目标，对区域IES系统进行了多阶段规划。文献[7]考虑了联络线峰谷差对IES系统的影响，建立了IES系统优化模型。还有文献以年规划成本最小化为目标，建立了双层规划数学模型，降低了混合优化模型求解的复杂程度[8，9]。文献[10]在考虑经济性的基础上，对IES系统规划运行的可靠性进行了评估。综上，在IES系统规划运行研究方面，大多对系统的经济性展开研究分析，因此IES系统规划运行方面的研究还需更加多样化。

太阳能作为一种源源不断的清洁能源，在IES系统中对其进行合理规划将会降低环境污染和系统成本[11]。然而，由于太阳能具有波动性和间歇性的特点，使得IES系统规划运行的难度进一步加大。文献[12]针对光伏接入IES系统的不稳定性，提出了一种供能可靠性的IES系统规划方法，通过仿真研究验证了所提方法的有效性。文献[13]建立了包含三层负荷预测的规划调度模型，以解决负荷不确定性对系统的不利影响。文献[14]基于碳交易机制，建立了以全寿命周期内系统成本最优为目标函数的IES系统多阶段规划模型，实现了IES系统中各设备的最优配置。文献[15]为提高风光装机比例，构建了以系统成本、风光利用率为目标的双层规划调度模型。由此可见，在IES系统中有效考虑太阳能接入的不确定性，将会提升系统的经济性和合理性。

综上，本研究提出了一种集成光伏发电系统、蓄热水箱以及内燃机的综合能源系统。

1 系统描述

1.1 参考系统

本研究中参考系统为分产系统，如图1所示。其中，用户电负荷由电网提供，热负荷由燃气锅炉(GB)通过换热器来满足，冷负荷则通过电制冷机(ASHP)向电网买电来满足。

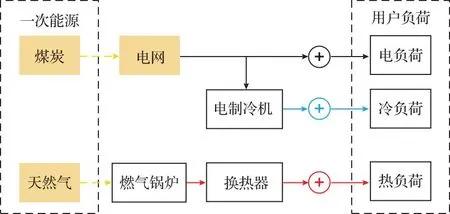
图1 分产系统示意Fig.1 Schematic diagram of production division system

1.2 综合能源系统

IES系统示意图如图2所示。内燃机(ICE)的高温烟气通过吸收式热泵(ABS)或者余热锅炉(WB)产生冷量或者热量。用户回水首先进入缸套水换热器被ICE的余热加热，其次进入WB吸收烟气余热。用户电负荷由ICE和光伏发电系统共同承担，系统产生的剩余电量上网。不足的电负荷则向电网购电来补充。此外，不足的冷、热负荷全部由GB来满足，多余的热量则储存在蓄热水箱中。

图2 综合能源系统示意Fig.2 Schematic diagram of integrated energy system

1.3 运行策略

IES系统根据以电定热的策略运行，ICE根据用户电负荷逐时调整其部分负荷率(PLR)，产生的余热则通过能量转换设备为用户供热。用户电需求首先通过光伏发电来满足，其次采用ICE发电量作进一步的补充，最后剩余的电负荷需求由电网来提供。此外，由于1—4月份以及11—12月份用户热负荷较大，其余月份用户的冷负荷较大，为使ICE的烟气余热被充分利用，在1—4月份以及11—12月份时，ICE的高温烟气通过WB加热用户回水，而其余月份则通过ABS来产生冷量。在系统供冷季节，用户回水不经过WB。用户剩余的冷需求和热需求都由GB来提供。

2 设备热力学模型

1)内燃机。ICE是综合能源系统中的重要组成部分，其通过燃烧天然气后产生的高温高压气体驱动发电机做功，进而将机械能转化为电能。此外，PLR对系统的运行过程有很大的影响，根据文献[16]，本文中关于PLR的定义如式(1)所示，ICE的能量转换关系如式(2)-(6)所示。

GICE=PICE/(ηm×ηg)

(2)

Qj=pj×(GICE-PICE/ηm)

(3)

Qs=ps×(GICE/ηm)

(4)

fg=GICE/HL

(5)

fs=(1+φ×β)×fg

(6)

式中，PICE为ICE的发电量，kW；RICE为ICE的额定容量，kW；GICE为ICE的天然气消耗量，kW；Qj为缸套水的热量，kW；Qs为高温烟气的热量，kW；ηm为机械效率；ηg为电厂的发电效率；pj为缸套水的热量占比；ps为排烟热量占比；fg为ICE的天然气流量，m3/s；fs为ICE的排烟流量，m3/s；HL为天然气的低位热值，为35600 kJ/m3；φ为过量空气系数，取2；β为空燃比，取9.52∶1。

2)光伏发电系统。光伏发电(PV)系统通过光电效应将太阳能转换成电能，其能量转换关系如式(7)所示[17]。

式中，Tpv，t为光伏板在t时刻的工作温度，K；Te为环境温度，K；Tn为光伏板的标称温度，取25 ℃；Radt为t时刻的辐照强度，W/(m2·K)；pv，t为光伏板在t时刻的转换效率；Ppv，t为t时刻的光伏发电量，kW；Apv为单个光伏板的有效集热面积，取2 m2。

3)缸套水换热器。用户回水流经缸套水换热器的过程中吸收的热量如式(8)所示。

Qj，out=Qj×ηj

(8)

式中，Qj，out为缸套水换热器的放出的热量，kW；ηj为缸套水换热器的换热效率。

4)余热锅炉。ICE的高温烟气流经WB加热用户回水，该过程中WB吸收的烟气余热如式(9)所示。

QWB=Qs×ηWB

(9)

式中，ηWB为WB的热回收效率。

5)吸收式热泵。ABS由ICE的高温烟气驱动，产生的冷量由式(10)所示。

CABS=QABS×COPABS

(10)

式中，QABS为ABS产生一定的冷量消耗的热量，kW；COPABS为ABS的能效系数。

6)空气源热泵。ASHP通过消耗一定的电量为用户供冷，其能量转换关系如式(11)所示。

CASHP=PASHP×COPASHP

(11)

式中，PASHP为ASHP产生一定的冷量需要消耗的电量，kW；COPASHP为ASHP的能效系数。

7)空气源热泵。GB的能量转换关系如式(12)所示。

QGB=GGB×ηGB

(12)

式中，QGB为GB产生的热量，kW；GGB为GB消耗的天然气量，kW；ηGB为GB的补燃效率。

8)蓄热水箱。系统产生的多余热量储存在蓄热水箱中，当系统供热不足时，蓄热水箱可补充供热。蓄热水箱的能量关系如式(13)所示。

式中，Qt，tank和Qt+1，tank分别为第t和t+1小时水箱内储存的热量，kW；θs为蓄热功率系数；θr为放热功率系数；Qs为水箱的输入热量，kW；Qr为水箱的输出热量，kW；Qs，max为水箱的最大蓄热功率，kW；Qr，max为水箱的最大放热功率，kW。

3 优化方案

3.1 综合能源系统容量规划优化模型

基于用户和系统之间能量供需的逐时平衡，采用遗传算法对IES系统经济性能进行了优化评估，并结合了一次能源消耗量和碳排放量的指标，对分产系统和IES系统的性能做进一步的比较。

3.1.1 优化变量

1)ICE的额定容量。RICE对综合能源系统的运行状态及其他设备选型有很大的影响。若RICE过大将导致系统处于低负荷运行状态，并且设备的投资成本增加，使得系统的效率及经济性较差；反之，若RICE过小，系统处于超负荷运行状态，对ICE的寿命也有不利影响。

2)蓄热水箱的容积(Vtank)。蓄热水箱储存系统产生的剩余热量，在系统供热不足时，放出热量为用户供热。Vtank越大，系统的投资成本越大。而Vtank较小时，会造成需要燃气锅炉补燃，在系统产热量剩余时还会造成热量的浪费。因此，合适的蓄热水箱容积将会提升系统的经济性和能效性。

3)屋顶光伏板的覆盖率(ppv)。ppv过大，系统的投资成本增加，经济性较差。而ppv过小时系统发电量减小，向电网的购电量增加，系统的能源利用率下降。因此，有必要对太阳能光伏板的个数进行优化。

3.1.2 约束条件

1)电功率平衡约束：

PICE，t+Ppv，t+Pgrid，t≥Puser，t

(14)

2)热功率平衡约束：

Qj，t+QWB，t+Qr，t+QGB，1，t≥Quser，t+Qabs，t+Qs，t

(15)

式中，QGB，1，t为GB逐时供热需热量，kW；Quser，t为用户逐时热负荷，kW。

3)冷功率平衡约束：

CABS+CGB，2，t≥Cuser，t

(16)

式中，CGB，2，t为GB逐时供冷需热量，kW；Cuser，t为用户逐时冷负荷，kW。

3.1.3 目标函数

针对分产系统和综合能源系统，建立了以年总成本(TAC)为目标的优化模型。系统年总成本包括系统的投资成本(Minv)、运行维护成本(Momc)、购买天然气成本(Mgas)、购电成本(Mele)以及碳税成本(Mtax)。

TAC=Minv+Momc+Mgas+Mele+Mtax

(17)

Momc=0.02×Minv

(20)

Gt=GICE，t+GGB，t

(22)

式中，ωj为第j型设备的成本回收系数；k为利率，取0.05；τj为设备寿命，取20 a；minv，j为第j型设备单位容量的投资成本，元/kW；Rj为第j型设备的额定容量，kW；yj为第j型设备的个数；mgas为天然气成本，元/kWh；Gt为t时刻系统的天然气消耗量，kWh；mele为购电成本，元/kW·h；Pbuy，t为t时刻的购电量，kW·h；msell为余电上网价格，元/kW·h；Psell，t为t时刻系统产生的剩余电量，kW；mtax为碳税，元/t；ρgrid为电网的碳排放因子，kg/kW·h；ρgas为天然气的碳排放因子，kg/kW·h。

3.1.4 评价指标

在考虑系统经济性能的基础上，通过年总一次能源消耗量(TPE)和年总碳排放量(TCE)对两个系统的能效性和环保性进行综合评估。

式中，ηe为火力发电效率；ηgrid为电网的电力传输效率。

3.2 优化算法

由于遗传算法具有内在的隐式并行式和较好的全局搜索能力，对于非线性、多变量优化问题有较好的优化结果[18]。因此本研究采用遗传算法对系统的年总成本进行优化，此外，加入并行计算进一步加快模型的求解速度。遗传算法的参数设置如下：种群代数为300，种群规模为100，变异概率为0.8，交叉概率见变异方程。优化变量的优化范围和优化步长见表1。

表1 优化变量范围及优化步长Table 2 Optimization variable range and optimization step

3.3 系统参数设置

系统中各个设备的技术参数如下：ηj为0.80，COPABS为0.70，COPASHP为4.00，ηWB为0.88，ηGB为0.85，θs为0.85，θr为0.85，Apv为2 m2，单个PV板的占地面积为5 m2，ηe为0.40，ηgrid为0.92，ρgrid为1.01 kg/(kW·h)，ρgas为0.22 kg/(kW·h)。

设备的经济参数如下(均指初始投资成本系数)：ICE为1046×μ(元/kW)，μ为美元兑人民币汇率，本文μ=6.5671；ABS为120(元/kW)；ASHP为970(元/kW)；GB为620(元/kW)；换热器为200(元/kW)；蓄热水箱为500(元/m3)；PV板初始投资成本系数为1500(元/块)[19]。

电价每天0∶00-6∶00，23∶00-0∶00时为0.38元/(kW·h)；7∶00-9∶00，15∶00-17∶00，21∶00-22∶00时为0.84元/(kW·h)；10∶00-14∶00，18∶00-20∶00时为1.32元/(kW·h)；余电上网价格(msell)为0.5元/(kW·h)。天然气价格(mgas)为0.22元/(kW·h)。

4 案例分析

针对办公建筑典型年的负荷特性，以经济性能最佳为优化目标，采用分产系统和IES系统为5栋办公建筑供能，评价了两系统的能效性和环保性。其次讨论了分产系统和IES系统逐月成本变化情况，最后针对IES系统分析了典型日的能量供需平衡。

4.1 研究对象

选取北京地区的一栋办公建筑作为研究对象，其屋顶面积为500 m2，如图3所示。其中，冷负荷集中在3月到11月，在这期间冷负荷先增大后减小，最大值在7月取得，约为501 kW。热负荷则主要集中在1—5月以及9—12月，最大值为325 kW左右，而用户电负荷在全年均匀分布，最大值约为68 kW。此外，北京地区典型年的逐时室外环境温度和太阳辐射强度如图4所示，可以发现，环境温度和太阳的辐射强度随着月份的增加先增大后减小，7月达到了全年的峰值期。

图3 办公建筑典型年负荷分布图Fig.3 Typical annual load distribution of office buildings

4.2 优化结果对比分析

得到优化结果为：RICE=227 kW，Vtank=129.25 m3，ppv=100%，因此在建筑屋顶装满光伏板时系统的经济性能最佳。分产系统和IES系统以经济性能为目标时的优化结果如下：IES系统的年总成本为1684183.14元，而分产系统的年总成本为2123350.17元。因此与分产系统相比，该IES系统的成本节约率为30.67%。在经济目标下，IES系统和分产系统的年总一次能源消耗量分别为5516142.65 kW·h和6056996.07 kW·h，而年总碳排放量为1345985.80 kg和2016668.61 kg，一次能源节约率和二氧化碳减排率分别为8.93%和33.26%。由此可见，在经济目标下，该IES系统的经济性能、能效性能和环保性能都显著优于分产系统的对应性能。

4.3 系统逐月成本变化情况对比分析

为进一步分析分产系统和IES系统的经济性，将年总成本中购电成本、购买天然气成本以及碳税成本进行逐月分析，两系统的逐月成本变化如图5所示(其中下角标ref代表参考系统的对应值)。

图5 分产系统和IES系统逐月成本变化图Fig.5 Monthly cost change chart of split production system and IES system

由图可知，针对单个系统来说，几种成本中碳税的成本占总成本的比例最小。IES系统的购电成本和碳税成本都显著低于分产系统的对应成本，而其购买天然气的成本高于分产系统的对应成本。其中，IES系统的购电成本相比分产系统而言降低幅度是最大的，7月时两系统购电成本的差值达到了最大，约为22.36万元。IES系统中ICE和PV机组全年的逐月发电量如图6所示，ICE的全年发电量约为838581 kW·h，而PV机组的全年发电量为197972 kW·h左右，为ICE发电量的23.61%，承担了全年用户电负荷的14.58%，有效减小了系统的购电量，因此极大地降低了系统的购电成本。

图6 IES系统中ICE和PV机组逐月发电量Fig.6 Monthly power generation of ICE and PV units in IES system

在IES系统中，由于不足的冷、热负荷都通过GB来满足，且ICE也需要天然气作为燃料。而分产系统中GB只需要给用户供热，因此IES系统的天然气购买成本远大于分产系统的天然气购买成本，且分产系统在4-10月的天然气购买成本几乎为0。碳税成本与系统对外的购电量和天然气购买量相关，IES系统中由于余热的回收利用以及PV机组的加入提升了系统的环保性能，从而减小了系统的碳税成本。

此外，由于1月和12月是热负荷的高峰期，而7月和8月是冷负荷的高峰期，因此系统的各部分成本在这几个月份会显著高于其余月份。4月和10月是冷、热负荷的低谷期，因此系统的各项成本在这两个月较低。

4.4 IES系统中典型日能量供需平衡

由于IES系统中含有蓄热水箱，而夏季时系统产热较少，蓄热水箱的作用并不明显，因此本节选取冬季典型日对IES系统中能量平衡进行了分析。冬季典型日的电量和热量供需平衡如图7所示。

图7 冬季典型日能量供需平衡Fig.7 Typical daily energy supply and demand balance in winter

由图7(a)可知，在负荷低谷期，ICE不启动，用户电负荷需求都通过电网购电来满足。电负荷高峰期时，ICE满负荷运行，同时PV发电机组白天时发电量增加，补充了一部分用户电负荷需求，减小了系统的购电量。在19∶00—22∶00，用户电负荷小于ICE额定容量，因此ICE部分负荷运行，减少了系统废电量的产生。图7(b)为冬季典型日的热量供需平衡，由于0∶00—7∶00期间，ICE不启动，因此这个阶段的热量需求都通过GB来满足。10∶00—17∶00，用户热负荷相对较低，IES系统产生的剩余热量被储存在蓄热水箱中。18∶00—22∶00，ICE处于部分负荷率的运行状态，IES系统供热不足，蓄热水箱放出热量补充用户剩余的热需求。在此期间，蓄热水箱放出的热量约为650.89 kWh，承担了当日用户热负荷的12.97%，有效的减小了系统用于供热的天然气购买量。