参量共振单摆的理论与实验研究

白在桥,王爱记,平 澄

(北京师范大学 物理学系,北京100875)

参量共振(Parametric resonance)是指通过周期性改变振子的参量(例如质量或弹性系数),使振子持续获得能量,振幅按指数形式发散的过程. 参量共振最直观的例子是荡秋千,若把秋千简化为单摆,荡秋千的人通过下蹲或站起改变重心的高度,使得等效摆长发生周期性变化,如果身体动作与摆振动的相位配合得当(摆到最低处附近站起,摆到最高处附近下蹲,动作频率是秋千频率的2倍),就可以对系统持续做功,使秋千越荡越高. 1831年,法拉第发现在竖直方向驱动圆柱形水桶可以在水面激发出水波,且水波的振动频率是驱动频率的1/2[1]. 这是已知最早的参量共振实验,现如今参量共振已被人们深入认识[2-5],并广泛应用于各种物理系统[6-10]. 本文参照荡秋千设计了参量驱动的单摆,利用微扰方法分析平衡点附近的运动,得到了轨道的解析表达式. 实验上,利用自制的二维位移传感器实时测量单摆的运动曲线,根据理论分析选用适当的模型提取轨道特征量,并将测量结果与理论公式进行比较.

1 实验原理

1.1 一般的参量共振

考虑周期性参量驱动的n自由度线性振动系统,其动力学方程的一般形式为

(1)

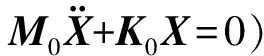
在控制参量空间(例如驱动频率-驱动幅度平面)内,能够出现参量共振的区域称为参量共振带.一般共振阶数k越大,对应的参量共振带越窄.此外,如果考虑阻尼,参量共振带还会进一步缩小.因此,实验一般只能观察到低阶的参量共振.对于单自由度系统,驱动频率在固有频率的2倍附近最可能出现参量共振.

1.2 参量驱动单摆

本文研究摆长l在l0(固定摆长)附近做小幅度周期性改变的单摆.为简单起见,假定摆在固定的竖直平面内运动,即只考虑单自由度振动.记摆角为θ,摆球的质量为m,并假设空气阻力与摆球速度成正比,系数为υ,则单摆的运动方程为

(2)

假定

l(t)=l0-Δlsin (ωt)l0[1-2εsin (ωt)],

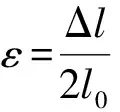
ω0[1+εsin (ωt)].

(3)

按此定义,sin (ωt)>0对应摆球高于平均位置.

使用自然单位m=g=l0=1,式(2)可无量纲化为

(4)

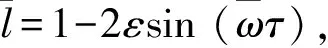
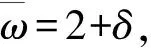
(5)

其中c1,c2为任意实数,

(6)

(7)

当|δ|=3ε时,为临界情况,由于控制精确性的限制,实验上无法严格满足,因此不予讨论．

当|δ|>3ε时,轨道包含2个频率略有差异的阻尼振动:

(8)

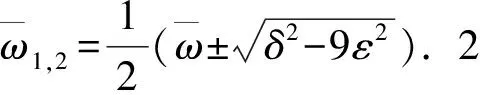
理解参量共振的关键是单摆与驱动的相位关系.将单摆的轨道写成以下形式:

(9)

(10)

其中,A为单摆的瞬时振幅,φ为单摆与驱动的相位差.如果没有扰动(即ε=γ=δ=0),A和φ都是常量.如果扰动足够小,A和φ会发生缓慢漂移,其演化方程可用平均微扰法得到:

(11)

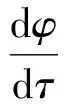
(12)

式(11)说明了相位差如何影响振幅的变化:当cosφ>0时,驱动力对单摆做正功,振幅有增加的趋势;当cosφ<0时,驱动力对单摆做负功,振幅有减小的趋势.其物理意义是单摆与驱动达到稳定的相位关系(相位锁定),驱动力持续对单摆做正功.

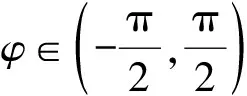
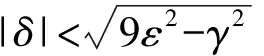
(13)

即振幅按指数形式发散,发生参量共振,λ1称为发散指数.参量共振带的边界由λ1=0确定,即

9ε2-δ2-γ2=0.

(14)

图1给出了式(14)与数值方法计算结果的比较,从图中可以看出,当ε<0.01时,二者几乎完全重合.

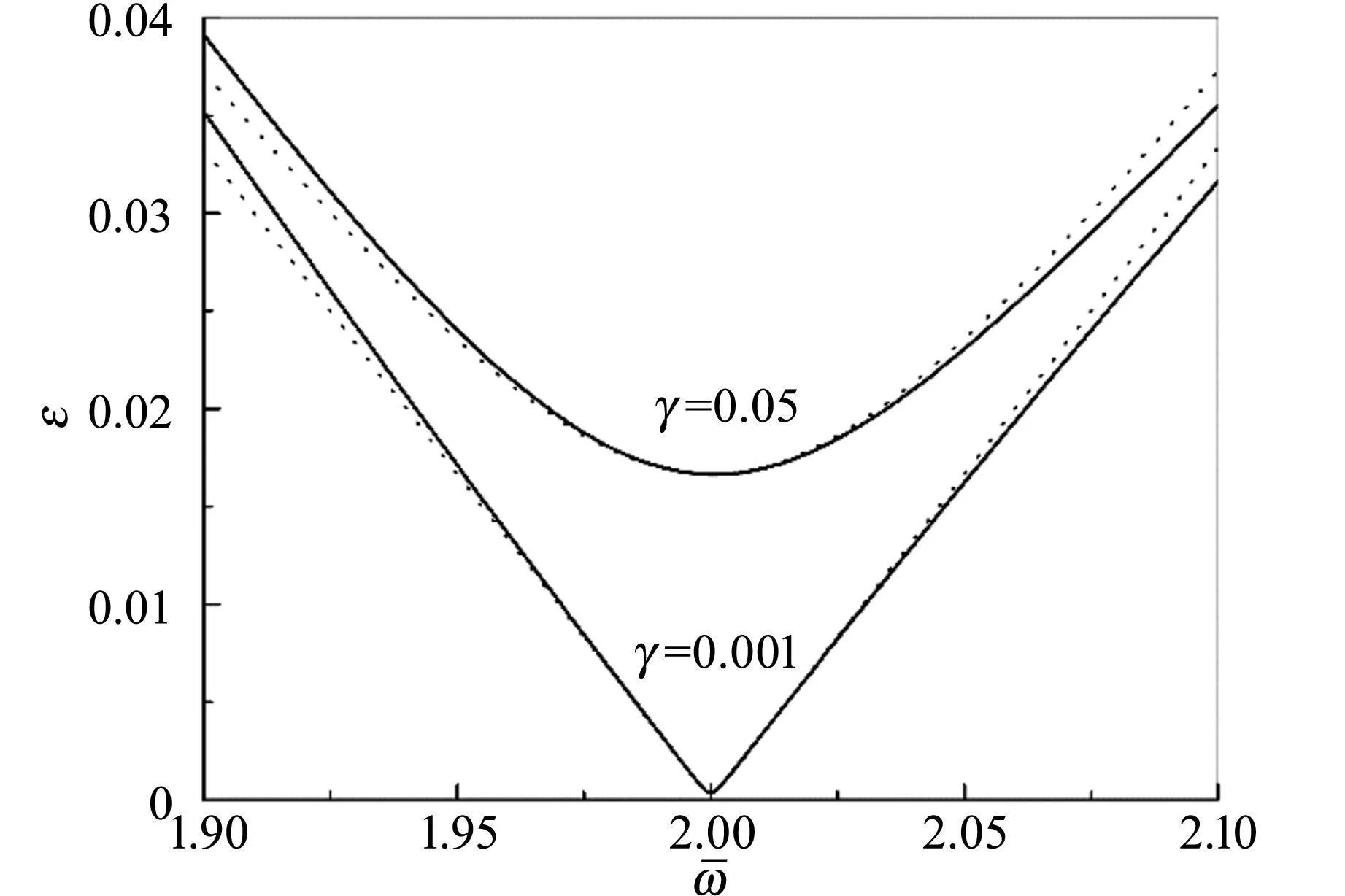
图1 不同阻尼系数对应的参量共振带的边界(实线为数值计算的结果,虚线为一阶微扰计算的结果)

当|δ|>3ε时,如果忽略指数衰减部分,轨道包络的最大振幅Amax=A1+A2,最小振幅Amin=|A1-A2|,调制深度为

(15)

当|δ|逐渐减小并接近3ε时,η→1,拍越来越明显.同时,拍的周期

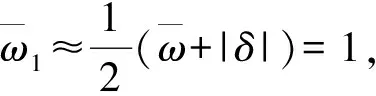
2 实验装置与方法

实验装置包含单摆、驱动和测量控制3个部分(图2),整体安装在门形支架上.

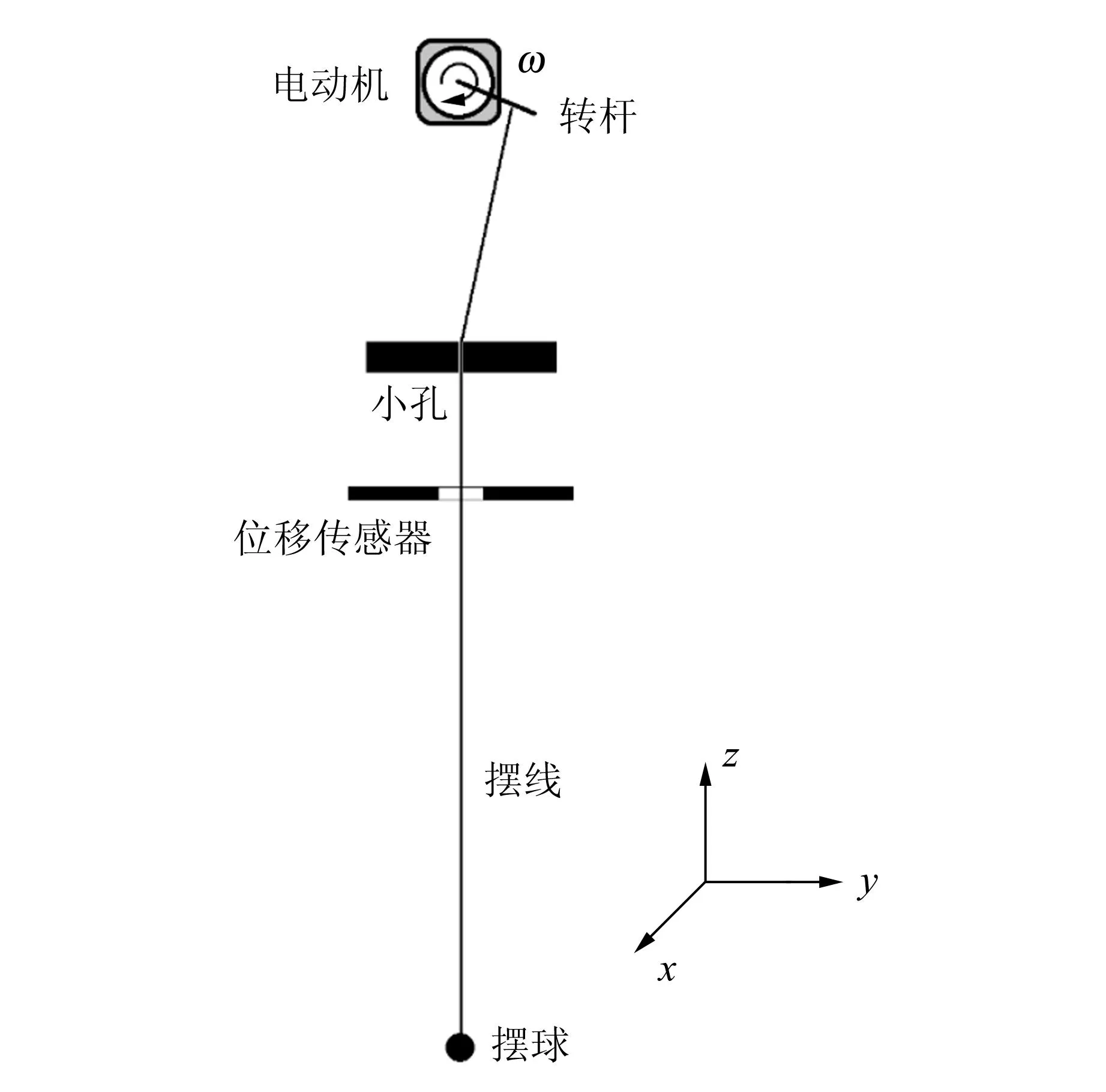
图2 实验装置示意图(未画金属偏心轮和涡流位移传感器)

摆球为黄铜球(直径25 mm,质量68 g),摆线向上依次穿过二维位移传感器和小孔(内径为0.3 mm,长度约为50 mm),最终结成环悬挂在转杆的螺钉上. 单摆有效摆长为摆球中心到小孔下端的长度. 穿过小孔部分摆线为直径0.2 mm的碳氟线,其余部分摆线是直径约为1 mm的PE鱼线,该设计是为了保证摆线可以在小孔中顺滑移动,同时尽量减小摆线在受力下的形变.

驱动部分由步进电动机和转杆组成. 转杆与电动机转轴固定,转杆上有8个螺孔,用于固定悬挂摆线的螺钉. 螺孔到中心的距离从7.5 mm到25.0 mm等差变化. 选择不同的螺孔相当于改变不同的驱动幅度(即Δl).

测量控制部分包括金属偏心轮、电涡流位移传感器、二维激光位移传感器和数据采集卡. 金属偏心轮套在电动机转轴上,用电涡流位移传感器测量偏心轮的边缘到传感器的距离,据此可以确定驱动的相位信号. 为了实时测量摆球在水平面内的偏转角度,用2个一维激光位移传感器(Panasonic HG-C1100)搭建了二维位移传感器(灵敏度约为0.01 mm). 激光位移传感器以模拟电压的形式输出测量结果,根据2个输出电压可计算出摆线与传感器二维平面交点的坐标. 实验中用数据采集卡(ART USB3131A)采集2个输出电压并转换为位移. 此外,数据采集卡有数字信号输出功能,实验中可用其控制步进电动机的转向与转速.

3 实验结果与分析

3.1 测量单摆参量

取螺钉到转杆中心的距离Δl=12.5 mm,并将螺钉转到最低位置(l=l0+Δl). 将摆球从一定角度释放,记录1 800 s的振动曲线. 由于位移传感器与小孔下端的距离约为200 mm,横向位移1 mm对应的摆角为1/200=0.005 rad. 因此为简单起见,以下用二维位移传感器测量的位移表示摆角.

图3为实测的单摆轨迹. 在较短的时间内(30 s),x和y方向上的位移均接近正弦曲线,从而在x-y平面形成稳定的椭圆[图3(a)]. 但随着时间增长,椭圆在逐渐缩小的同时,其主轴方向会轻微转动[图3(b)],该转动看起来和傅科摆类似,但多次测量发现振动面转动的速度和方向具有一定的随机性,造成该现象的主要原因可能是装置的旋转对称性存在轻微的破缺(例如小孔不够圆).

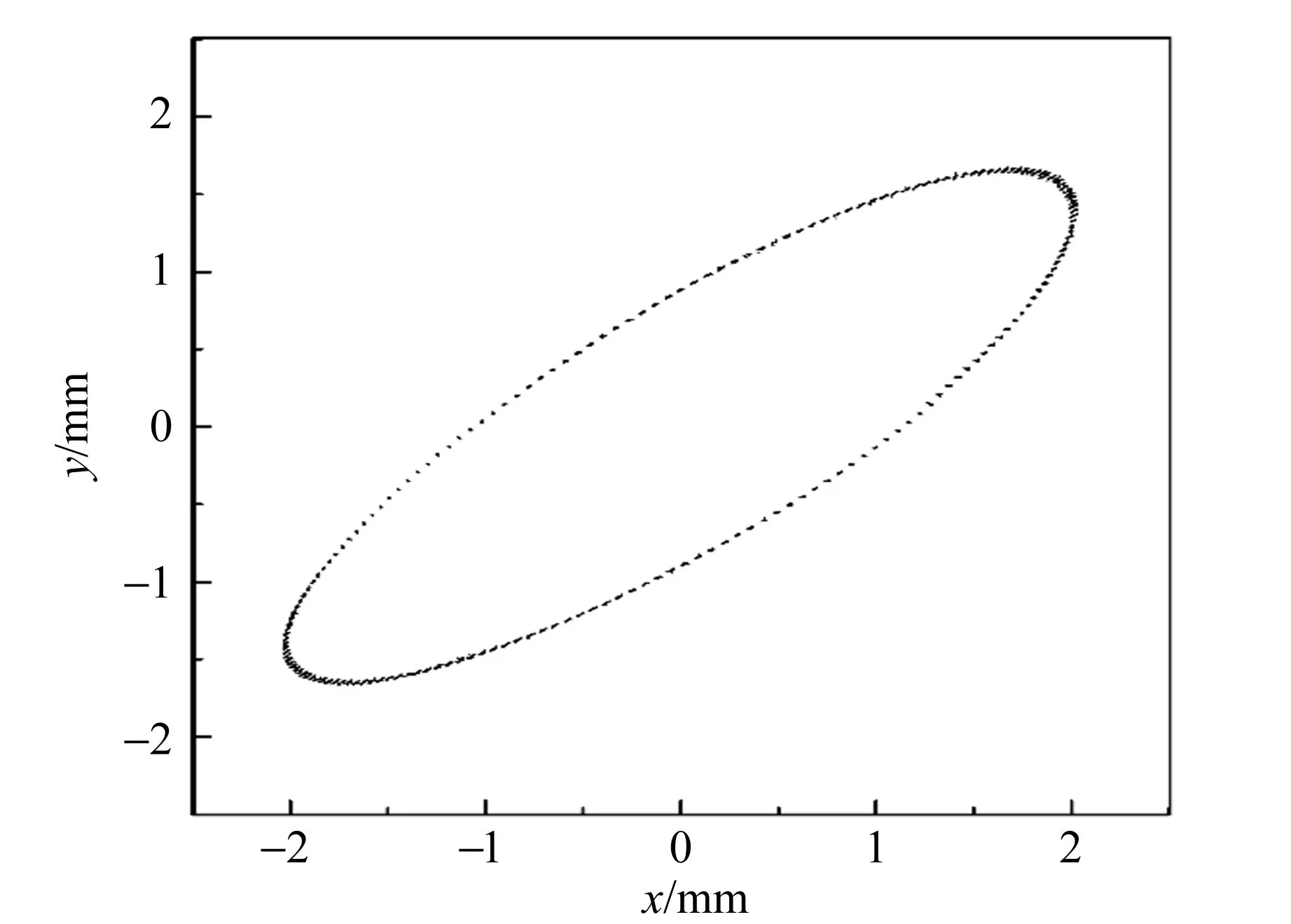
(a)t=30 s

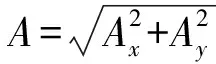
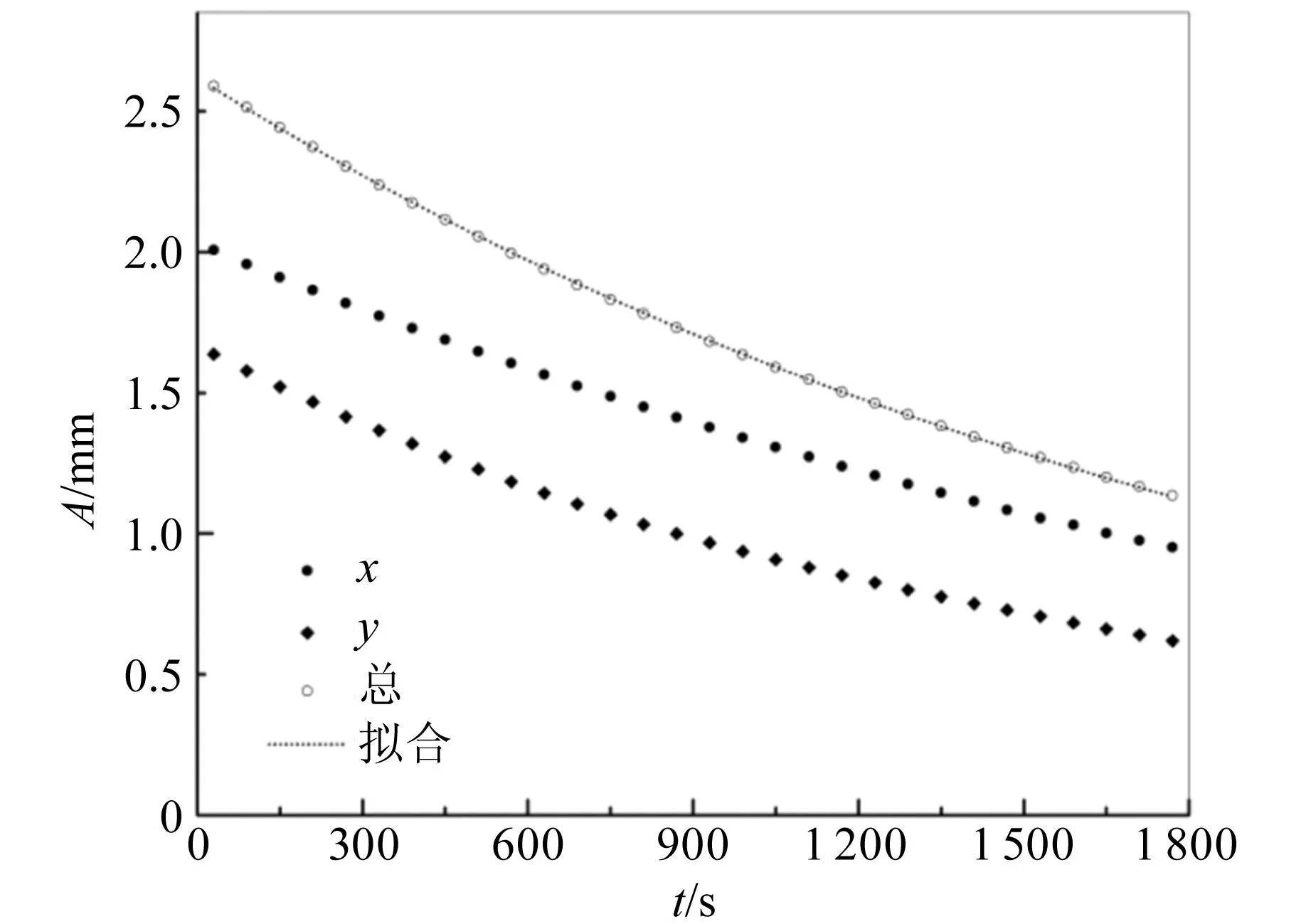
图4 单摆的振幅衰减曲线

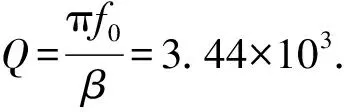
表1 单摆参量计算

由表1可知:x,y方向测量的频率在10-5Hz位数上有差别,后面的实验显示这种差别有一定的可重复性.为了简单起见,将这种差别视为实验装置不完美引起的频率不稳定性,同时将x(t)和y(t)视为对轨道的2次采样.因此,取2个频率的平均值作为单摆频率的最佳估计.此外,上下2个位置的衰减系数β也在10-5s-1位数上有差别,故同样取二者的平均值作为衰减系数的最佳估计.在此基础上,可以计算中心频率f0、频率改变幅值Δf以及品质因数Q,它们与微扰计算用到的无量纲系数的关系是:ε=Δf/f0,γ=1/Q.对于以上计算结果,讨论如下:

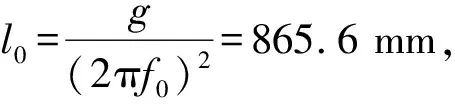
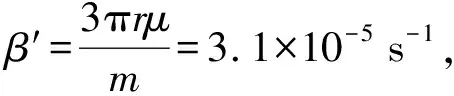
3)根据前文的理论分析可知,发生参量共振的条件是:1.059 781 Hz1.082 46 Hz或者fd<1.059 78 Hz. 其中,fd为驱动频率. 这3个区间之间存在2个宽度为10-6Hz的区域,对应单摆可以和驱动相位锁定,但受阻尼影响不会发生参量共振. 考虑到系统频率的不稳定性在10-5Hz量级,因此本实验装置不能观察到这类轨道.

3.2 参量共振轨道

3.2.1 参量共振产生的过程

保持Δl=12.5 mm,设定驱动频率fd=1.071 Hz≈2f0,在摆幅足够小的条件下启动步进电动机,记录单摆的位移曲线,结果如图5所示. 由图5可知,振幅按指数形式增长,且x方向和y方向的位移之比基本不变,这表明轨道在竖直平面内.

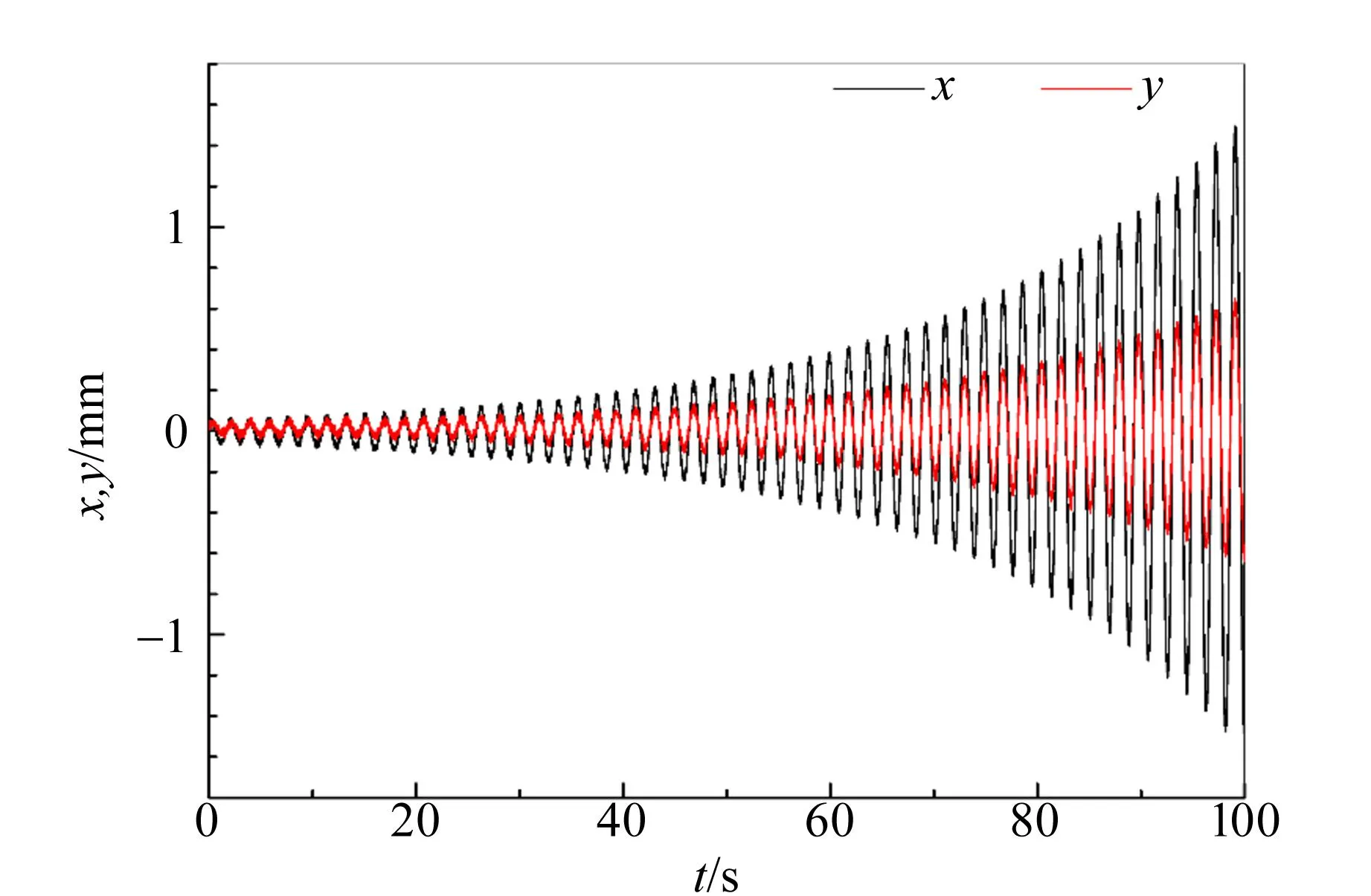
图5 参量共振轨道

为显示单摆与驱动相位的关系,以x(t)为横轴,驱动信号为纵轴画图,如图6所示.由于驱动信号正比于摆长的变化量,在小摆角近似下也与摆球z方向的位移相差1个正的比例系数,因此在横向(x轴)与纵向(z轴)各相差1个比例因子的情况下,图6可以理解为从侧面观察到的摆球运动轨迹,且可以清楚地看到摆球在平衡位置附近向上运动,在最大摆角附近向下运动,轨迹为∞形,且摆幅逐渐增大.

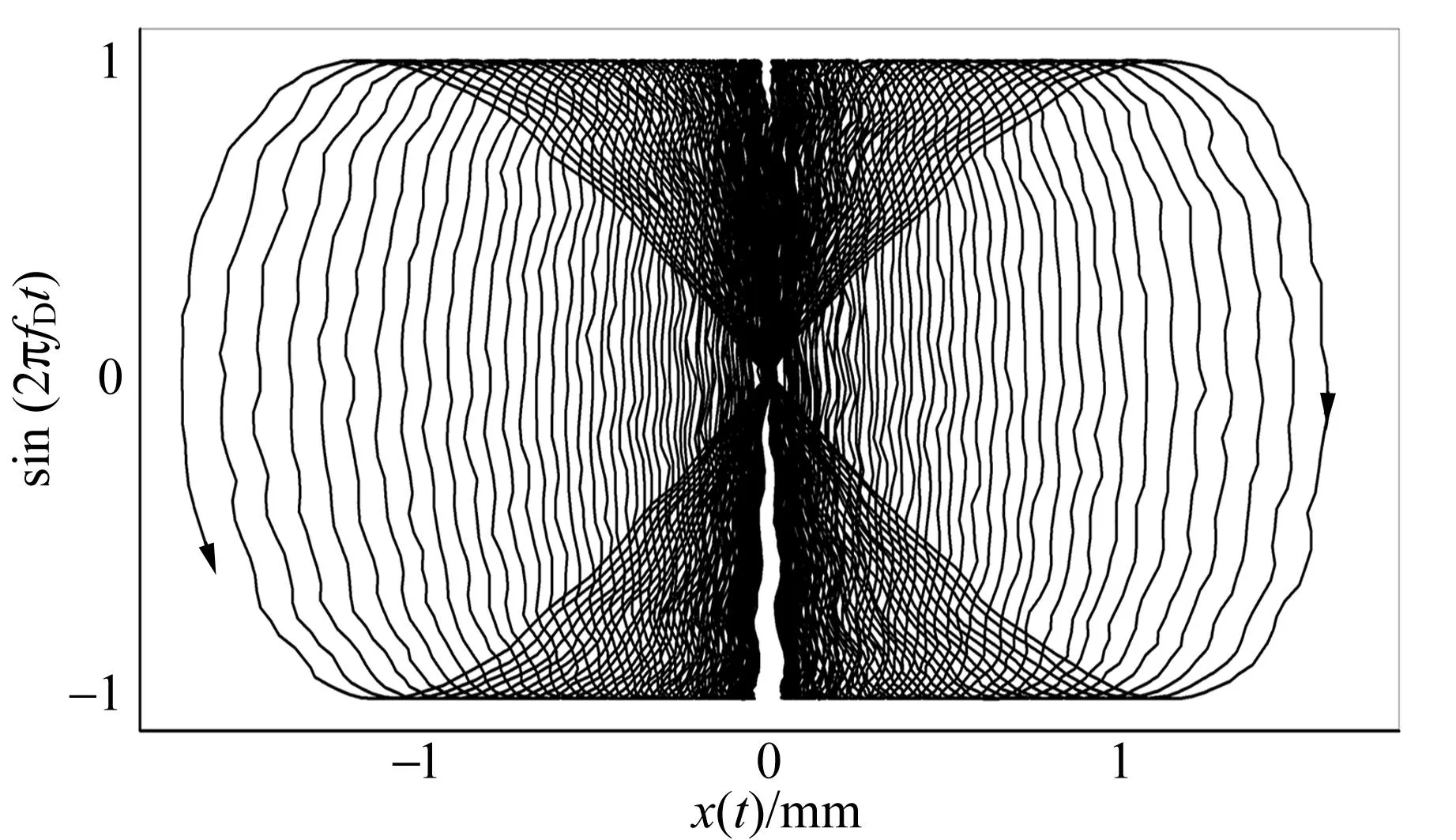
图6 参量共振单摆的高度与摆角的关系

为了更好地描述参量共振产生的过程,计算了单摆的瞬时振幅A和相位差φ.方法是取以t为中心,长度为tw=4/fd的时间窗口,用频率为fd/2的正弦函数拟合窗口内的位移曲线,得到振幅A(t)和相位φp,用频率为fd的正弦函数拟合驱动信号,得到驱动相位φd,再按

φ(t)=2φp-φd

(16)

计算瞬时相位差,结果如图7所示.可以看出x,y方向上相位差的初始值并不相等,但相位差会随着时间t逐渐趋向一致,即达到φ的稳定不动点.当φ足够靠近稳定不动点后,振幅的增长率基本为常量.

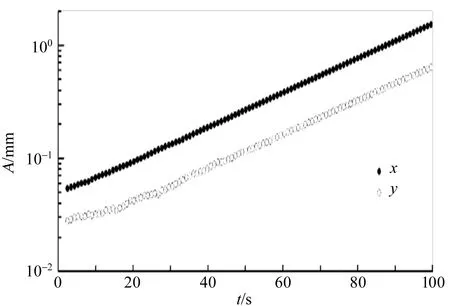
(a)瞬时振幅

需要指出,振幅指数发散与经典力学中的相空间面积守恒以及考虑到阻尼后相空间面积的收缩并不矛盾.因为相空间面积守恒,半径(振幅)方向上的增长必定导致角度(相位)方向上的收缩,即φ会逐渐收敛到1个点.另一方面,式(5)中包含指数衰减的解,λ1+λ2=-γ<0保证了相空间面积收缩.

观察衰减轨道的方法是:当轨道振幅开始稳定增长且转杆处于水平位置(φd=0,π)时,让步进电动机反转(φ→φ+π),按此方法记录的轨道如图8所示,可以看到电动机反转(t=153.48 s)后,振幅会经历短时间的衰减,但经历长时间后仍会发散.

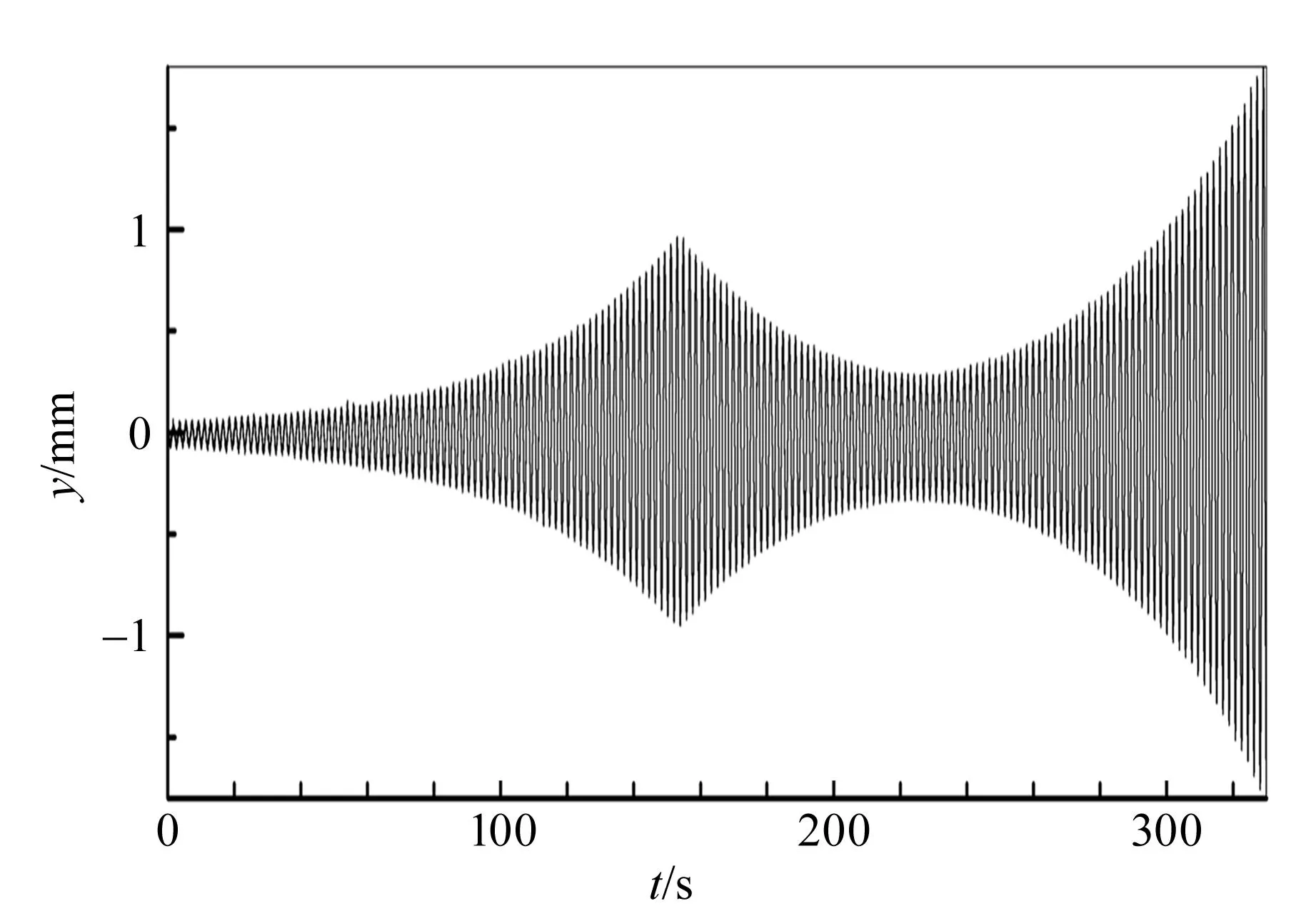
(a)位移曲线

3.2.2 参量共振的频率特性

保持Δl=12.5 mm不变,改变驱动频率fd,当摆幅足够小时加入驱动,记录参量共振曲线,并用A0eλ tsin (πfdt+φp)+c拟合振幅稳定增长阶段的数据,得到发散指数λ,根据式(16)计算相位差φ(t),所得结果见表2.

表2 不同驱动频率下参量共振轨道的发散指数与相位差数据

回到物理量纲,式(6)和式(7)应写成

(17)

(18)

为了使理论曲线与测量结果符合得更好,取f0=0.535 45 Hz(较表1中数值减小1.1×10-4Hz),这种微调体现了系统频率的不稳定性,可以看出经过参量微调后,理论曲线与实验数据吻合较好,如图9所示.

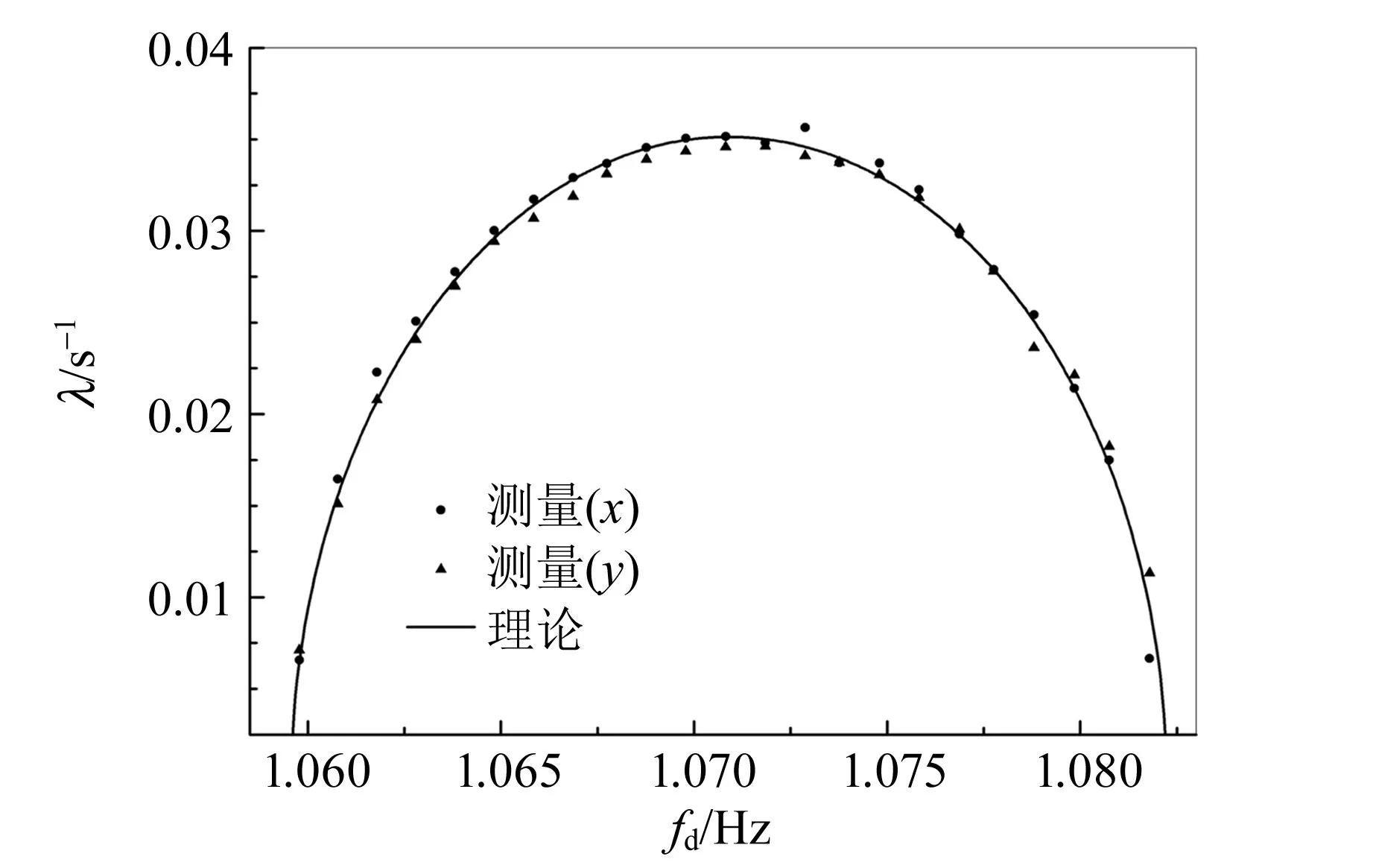
(a)发散指数与驱动频率的关系

3.2.3 发散指数与驱动幅度的关系

将驱动频率设定在参量共振带的中心(fd=1.071 Hz),改变Δl,测量参量共振轨道的发散指数,结果如表3所示.

表3 不同驱动强度下的轨道发散指数

由于Δf正比于Δl,任意Δl对应的Δf为

(19)

而在共振带的中心,一阶微扰计算给出

λ=3πΔf-β,

(20)

将测量结果与微扰计算进行比较,结果如图10所示,可以看出二者符合较好.

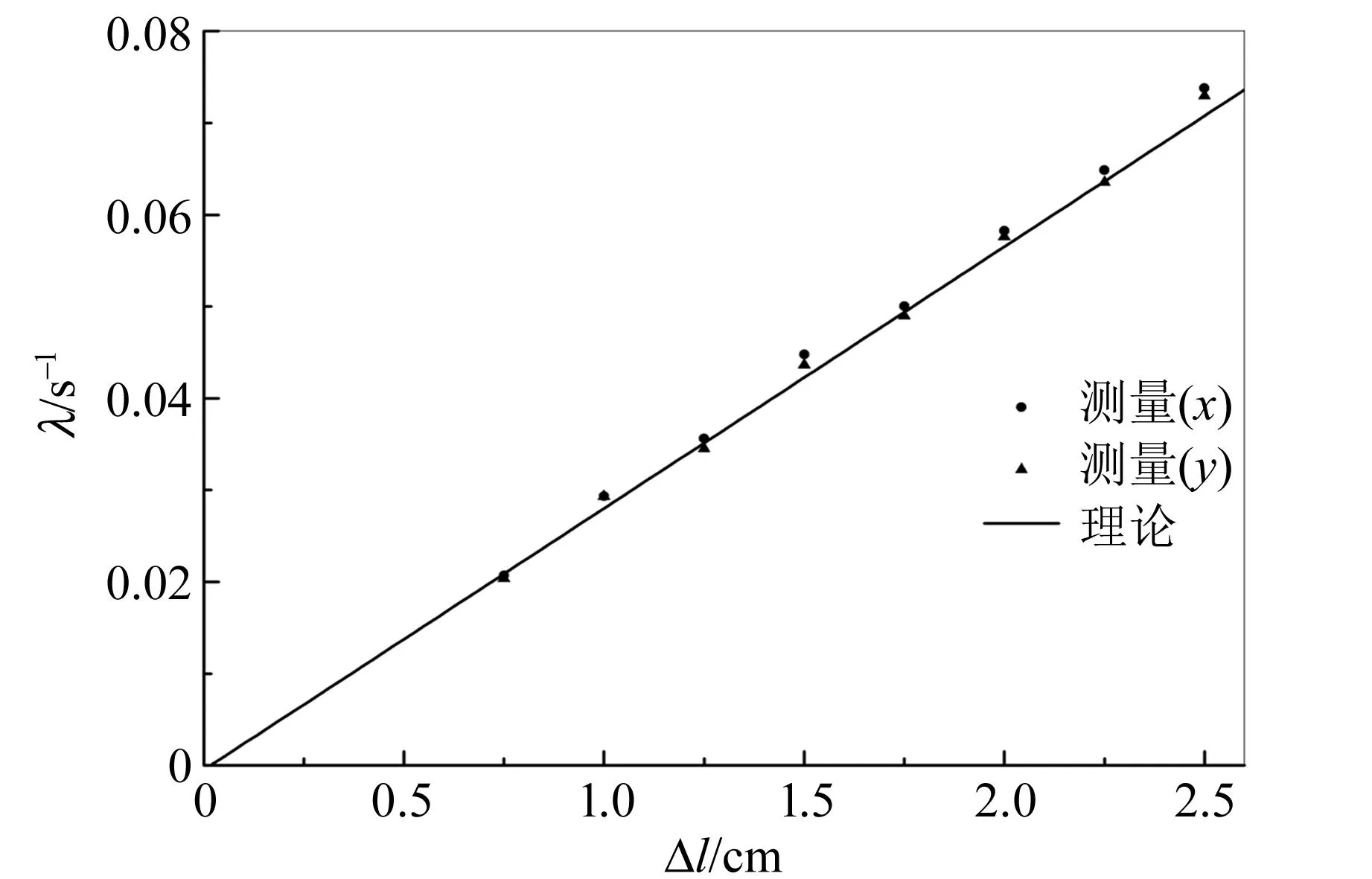
图10 参量共振带中心发散指数与驱动幅度的关系

3.3 参量共振带外边缘的轨道

在参量共振带的外边缘,如果单摆有初始摆角,在驱动作用下摆幅会在匀速衰减背景下发生周期性变化.

图11(a)为Δl=12.5 mm,fd=1.059 Hz时的轨道. 启动驱动时,让单摆只在x方向振动,故图中只有x分量.在记录时间范围内,振幅的衰减并不明显,最显著的特征是长度约400 s的拍.

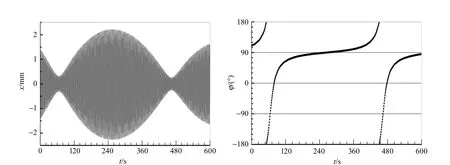
(a)位移曲线 (b)瞬时相位差图11 参量共振带下边缘附近的轨道

图11(b)为该轨道的瞬时相位差随时间变化的曲线,可以清楚地看到当φ∈(-90°,90°)时振幅增大,当φ∈(90°,270°)时振幅减小. 另外,φ的变化率并不均匀,特别是在90°附近变化很慢;对称的,在参量共振带的上边界之外,φ会在-90°附近变化很慢. 以上现象体现了系统的连续性,此时的驱动频率非常靠近参量共振带的下边界,如果驱动频率再略高,在略小于90°的位置就会存在1个稳定的不动点.

参照式 (8),参量共振带外的轨道可以用下面的函数形式拟合:

x(t)=e-β′t[A1sin (2πf1t+φ1)+

A2sin (2πf2t+φ2)]+b,

(21)

理论上

β′=β,

在参量共振带的上、下边界外各采集了10条轨道,每条轨道都可以用式(21)很好地拟合,最佳拟合参量见表4.

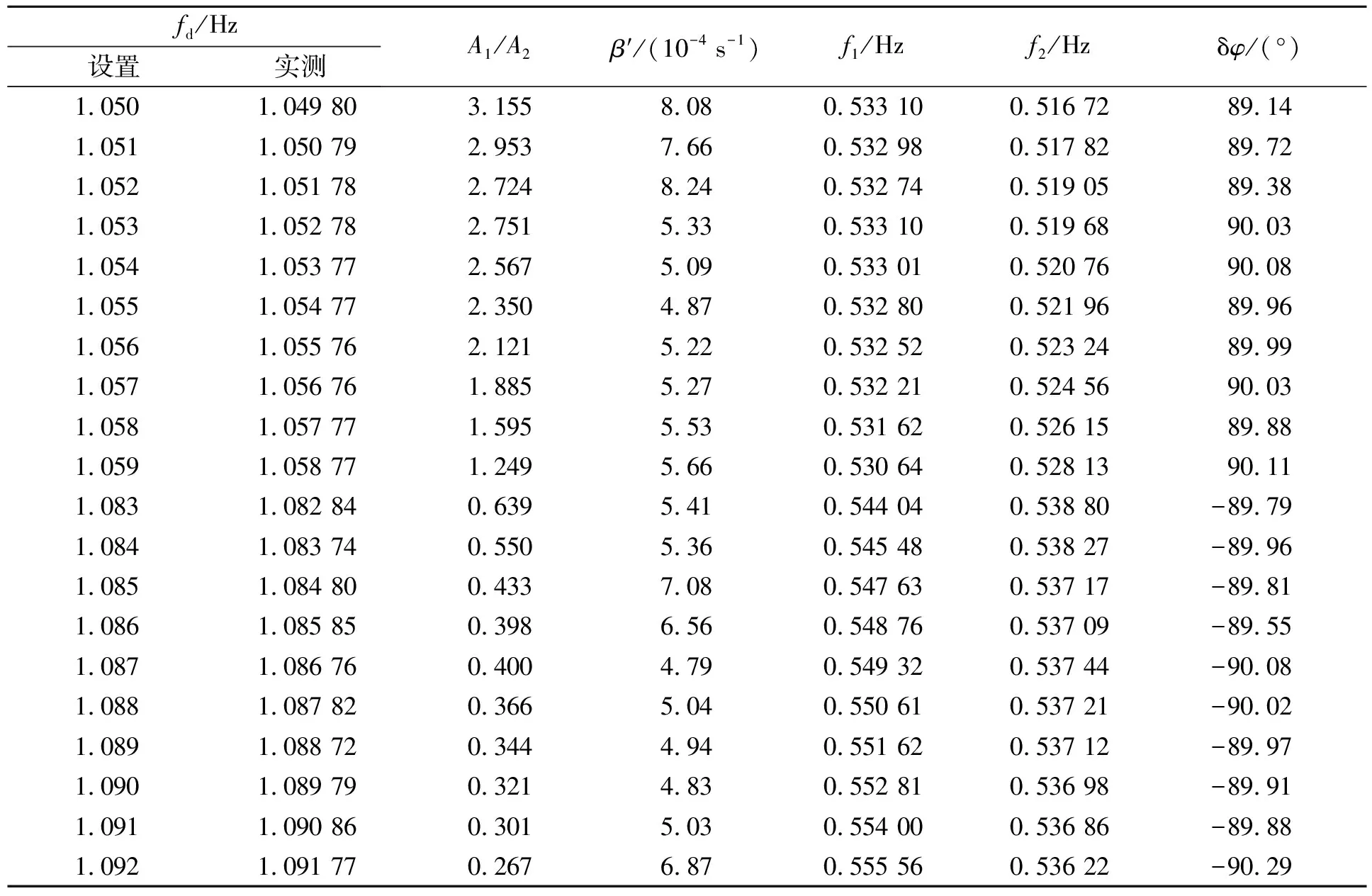
表4 参量共振带之外轨道的特征量测量

图12比较了f1,2的拟合值与计算值(虚线为渐近线),计算用到的参量与图(9)中的相同.可以看出理论和测量的整体趋势符合较好,不过理论曲线整体约偏右4×10-4Hz,或者f0应减小2×10-4Hz.

图13为包络调制深度为

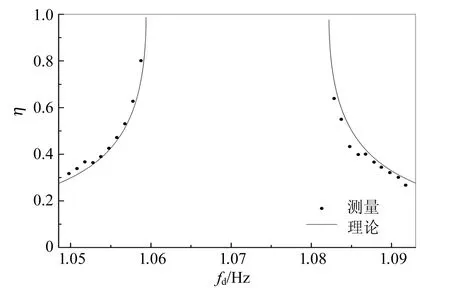
图13 调制深度的测量结果与理论曲线比较

的实测结果与理论计算的对比曲线. 与图12类似,理论和测量整体趋势符合,但整体略微右偏. 造成偏离的原因可能是在实验过程中摆长发生了轻微变化 (增加0.6 mm).

4 结束语

本文用步进电动机驱动单摆的摆长发生周期性变化,对参量共振现象进行了细致的研究. 理论上,对线性化的方程进行了一阶微扰计算,得到了发生参量共振的条件和平衡点附近轨道的分类以及轨道特征量与驱动频率、驱动幅度的依赖关系. 实验上,利用自组的二维激光位移传感器实时测量了单摆的运动,并对参量共振和接近参量共振的轨道进行了定量测量,所得结果均与微扰计算给出的公式很好符合. 参量共振的理论涉及较多的数学计算,增加了学生对其物理本质的理解难度. 本文引入了单摆与驱动信号的瞬间相位差,将参量共振表征为相位锁定现象. 通过实测相位差随时间的变化曲线,为理解参量共振的发生机制提供了直观的图像. 参量共振带内的轨道是振幅随时间指数增长的振动,接近参量共振带轨道(在阻尼可以忽略的情况下)是包含2个频率的准周期运动,这2类运动在大学基础物理实验中很少涉及. 从教学的角度,利用单摆研究参量共振具有2个优点:a.运动图像直观、实验现象明显;b.力学模型简单,便于理论分析. 除了摆长周期性变化,单摆的参量驱动方式还可以让悬挂点上下周期性运动或者在竖直方向对摆球施加周期性的外力. 具体到实验装置则有更多的设计方案. 本文装置可以改进之处:a.提高装置的稳定性,提高测量结果的准确性;b.提高位移传感器的测量范围,使之可以研究大振幅运动;c.将单摆扩展为双摆,研究多自由度体系的参量共振.