基础实验试题B:测量透明固体和液体材料的折射率以及柯西关系
2024-03-06陈梓平
陈梓平,马 波
(中山大学 物理与天文学院,广东 珠海 519082)
折射率与光的波长有关的现象叫做色散. 利用色散可以分光,即把复色光分解为单色光而形成光谱. 1672年,牛顿利用三棱镜将日光分解为彩色光带,这是现知最早的观测色散现象的实验. 广义上来讲,任何物理量只要随着频率(或波长)的变化而变化,便称为色散[1],例如旋光色散等. 色散现象在光谱分析领域有广泛的应用,利用色散光谱分析可以分析物质的成分、结构和研究其反应过程;而在光通信领域中,光在光纤中传输时也会因色散而导致信号失真和衰减,因此通过研究光的色散现象、折射规律,可以开发出各种抑制和补偿色散的技术,提高光纤通信的传输速率及距离[2];通过色散原理测量星系的蓝移或红移,在天文学领域具有重要研究意义,可以帮助科学家了解宇宙的膨胀速度. 因此研究光的色散,即光在不同介质中的折射率具有广泛的应用价值.
分光计的基本光学结构是许多光学仪器(如棱镜光谱仪、光栅光谱仪、分光光度计、单色仪等)的基础,其在物理实验中既能够锻炼学生的基本实验技能,又能培养学生应用理论知识解决实际问题的能力. 因此,分光计是大学物理实验的重要实验仪器[3].
第9届全国大学生物理实验竞赛珠海赛区基础题B选择了用分光计测量透明固体和液体材料的折射率. 该实验是在常规的大学物理实验内容的基础上,加入透明比色皿正方体容器,设计实验方案测未知液体的折射率. 试题一方面考查学生基础知识的熟练掌握程度;题目符合教学高阶性、创新性、挑战度和阶梯性的要求,在大学物理实验的基础上进行拔高,提出复合光路的实验设计,培养学生知识拓展、举一反三的能力和物理学科核心素养[4].
1 仪器及竞赛题目
1.1 仪器耗材介绍
本实验以分光计为主要仪器,提供了光栅、汞灯、钠灯配套元器件,如表1和图1~2所示. 搭建实验系统:直接使用三棱镜测出三棱镜对应不同波长光线的折射率;将三棱镜置于容器内,并注入液体,测量未知液体对应波长的折射率.

图1 汞灯和分光计的实物图

图2 正方体空腔容器
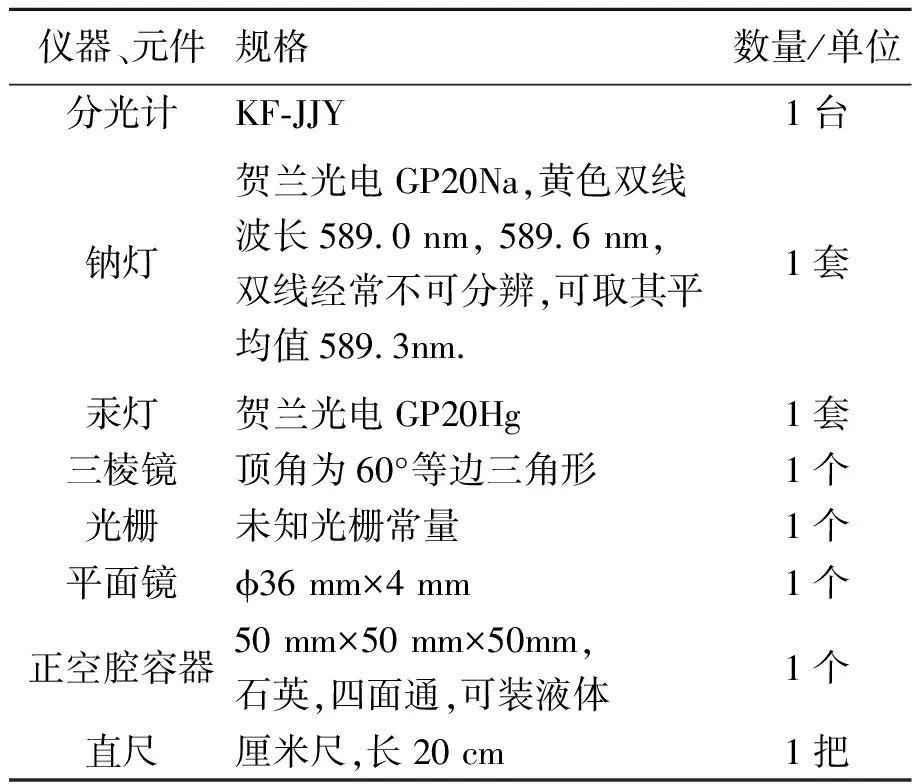
表1 主要实验器材列表
1.2 竞赛题目
1)利用光栅方程,使用分光计、未知光栅常量的光栅、给定黄光发射线波长的钠光灯,测量汞灯中各发射线的未知波长. 请简述测量原理,并测量发射线在三棱镜中的折射率.(可提供锦囊1)
2)设计实验方案用以测量汞灯的发射线在某未知液体中的折射率,详细写出设计方案.(可提供锦囊2)
3)使用上述方案进行实际测量,要求至少使用5条不同的汞灯发射线,数据记录需符合规范要求.
4)基于已测数据,使用最小二乘法,分别拟合三棱镜及未知液体2种材料的柯西公式.(可提供锦囊3)
5)误差分析讨论:假设给定的三棱镜顶角有1°的误差,简单讨论并估算三棱镜的n(500 nm)的误差;假设给定的钠灯黄光谱线波长有0.1 nm的误差时,简单讨论并估算三棱镜的n(500 nm)的误差.
2 考核点
2.1 基础理论知识及常见光学仪器的应用
在光学实验教学中,常常发现即使学生已充分预习,但在实际操作时仍不能很好地操作仪器,例如利用分光计进行测量的实验,其难点在于:
1)分光计的调平. 分光计的调节基于光学实验中最基本的光路要求——等高同轴共心,载物台平面和望远镜光轴平行,望远镜光轴和准直管光轴水平且在一同直线上. 但在实际教学中发现,学生进行光学实验操作时的基本准则意识较弱,经常在不知晓目的时盲目调节仪器.
2)光的色散理论和折射率的测量单靠理论理解起来较为抽象,且光线透过狭缝后进入准直管和望远镜光管,整个系统要求学生对光路有具象建模的过程,以清晰准确地把握光路的走向,从而快速找到出射光线. 由于学生光路建模的能力相对较弱,从而导致学生很难找到产生最小偏折角的折射光线. 另外圆游标角度值的读数也是分光计教学中的薄弱点.
试题考核了学生的实验操作能力,能否灵活利用所提供元器件进行实验
2.2 复杂光路的分析能力及光学建模、方案设计
学生在理解分光计常规实验内容的基础上,了解不同透明介质材料对同一波长的光的折射能力强弱不同,通过光路具象建模,懂得如何将所提供的元器件进行搭配才能得到折射光线.
试题考查了学生的知识迁移能力,方案设计的逻辑性、合理性、创新性.
2.3 数据测量及处理
利用所设计的实验方案测量汞灯发出的5条不同波长的发射线在未知液体中的折射率,考查学生实验操作及数据记录的规范性和完整性.
通过所测数据,选择5条肉眼能识别出的汞灯发射线,利用做小二乘法拟合计算得到折射率的柯西公式[5].
2.4 误差分析与讨论
考查在假定情况下的误差分析,以及基于误差分析结果规范表述实验结果的基本素养.
3 实验原理、测量方法及解题参考方案
3.1 知识点
折射率是物质中的原子和电子与电磁波相互作用的重要物理参量. 不同颜色的光在透明介电材料内存在色散现象,是由于不同颜色的光在同一材料内的折射率不同. 假设在可见光区域,大部分透明材料的折射率满足柯西关系[1]:
(1)
其中,n(λ)为对应波长的光在该材料中的折射率.在可见光波段中,通过柯西关系,可计算出不同波长光的折射率.
3.2 测量三棱镜折射率和最小偏折角法
对于题目1),可以使用分光计,利用光栅和钠光灯(已知发射线波长)测量得出汞灯中若干条发射线的波长.该测量中需要使用光栅方程
dsinφ=kλ,
(2)
其中,d是光栅常量,φ是谱线的衍射角,k是光谱级数,λ是对应谱线的波长.
应用最小偏折角原理测量折射率.当棱镜内的折射光线行进方向和三棱镜的底边平行时,入射光线和出射光线之间会产生最小的偏折角度.根据简单的折射规律和几何关系,推导出棱镜的折射率为[1]
(3)
其中A为三棱镜顶角,题中给出A=60°.测得汞灯的不同谱线波长及对应的三棱镜折射率如表2所示.

表2 测量所得汞灯中5条发射线参考波长及利用最小偏折角法测量发射线对应的三棱镜折射率
3.3 测量透明液体材料折射率和最小偏折角法
针对题目2)和3),可参考以下方案解答.
题目中提供了三棱镜、正方体比色皿容器、未知液体. 可以先将三棱镜放入比色皿,且三棱镜磨砂底面紧贴正方体容器的一个侧面,再将未知液体倒入正方体空腔容器内,组成组合式的分光元器件,发生最小偏折角情况下,棱镜内光线行进方向和棱镜/比色皿底边平行,如图3~4所示.

图3 组合式分光元器件示意图

图4 组合式分光元器件实物图
当光线分别从正方体左右两边入射和出射时,整个系统组成左右对称的光学系统,因此仍然可以像3.2节中应用最小偏折角原理来测量折射率:当三棱镜中的光线行进方向和三棱镜的底边平行时(图3),入射光线和出射光线之间会产生最小的偏折角度.
利用等边三角形和正方形的特殊几何关系,在光线从空气进入液体的分界面1和从液体进入三棱镜的分界面2(如图3中蓝色圆圈标识所示)分别应用折射公式,可以得到:
(4)
(5)
其中,A是三棱镜顶角,B是入射光线在第一个分界面——从空气进入未知液体后的折射角,n0是空气折射率(假设为1.0),nL是未知液体折射率,nP是3.2节中测量得到的棱镜材料的折射率.将式(5)除以式(4),利用三角函数关系,可得
(6)
将此部分实验测量得到的最小偏折角δm2代入到式(6),可以求出B,再代入式(4),则可以得到未知液体的折射率为
(7)
测得汞灯不同谱线对应的折射率如表3所示.

表3 利用最小偏折角法测量所得5条发射线对应的未知液体的折射率
注意,计算过程中将正方体比色皿容器做理想化处理,假设容器壁的厚度均匀,内外壁面严格平行,不影响光的行进方向,所以可以忽略正方体容器侧边折射的影响.
3.4 数据处理
将式(1)中的λ-2替换为x,柯西关系变为
n(λ)=a0+a1x+a2x2.
(8)
测量汞灯5条谱线数据对应5个点,这些点到式(8)代表的曲线的距离的平方和,为即残差平方和
(9)
为求出使R2取极小值所对应的多项式系数ak,令R2对ak的偏导数为0,可得3个线性方程(k分别取0,1,2):
(10)
求解式(8)~式(10),即可得到柯西关系多项式的最佳拟合参量a0,a1和a2.
代入测试实验时获取的数据,波长选取nm作为单位,可以计算得到2种不同材料的柯西关系参考值分别为
(11)
(12)
最终拟合得到的未知液体的柯西关系图如图5所示.拟合所得的折射率数据的残差在1×10-4数量级.

图5 未知液体的柯西关系拟合图
3.5 误差分析
在假设实验其他部分测量均没有误差,且柯西关系严格成立的前提下,分别讨论当三棱镜的顶角有1°的误差和钠光灯的谱线波长有0.1 nm的误差2种情况下,波长为500 nm的可见光在三棱镜中的折射率n的误差.
考虑到前面题目内容较多,花费时间较长,此处误差分析只要求简单讨论和估算,选手可以用类似蒙特卡罗式的误差估计方法A:将顶角换为59°和61°分别计算下n的值,以及使用500.1 nm和499.9 nm分别代入柯西关系,就可以估算出n的误差. 若采用方案B:利用误差传递公式,计算得到不确定度结果,则需要做大量的计算.
4 结果与评论
4.1 答卷得分统计
本次竞赛共有53组队伍选做基础实验试题 B.选手的得分情况如图6~8所示,最终只有10%左右的选手能顺利完成所有实验内容反映出此竞赛题目的难度是偏高的,具有高阶性和挑战度. 从第1),2),4)题的统计结果来看:
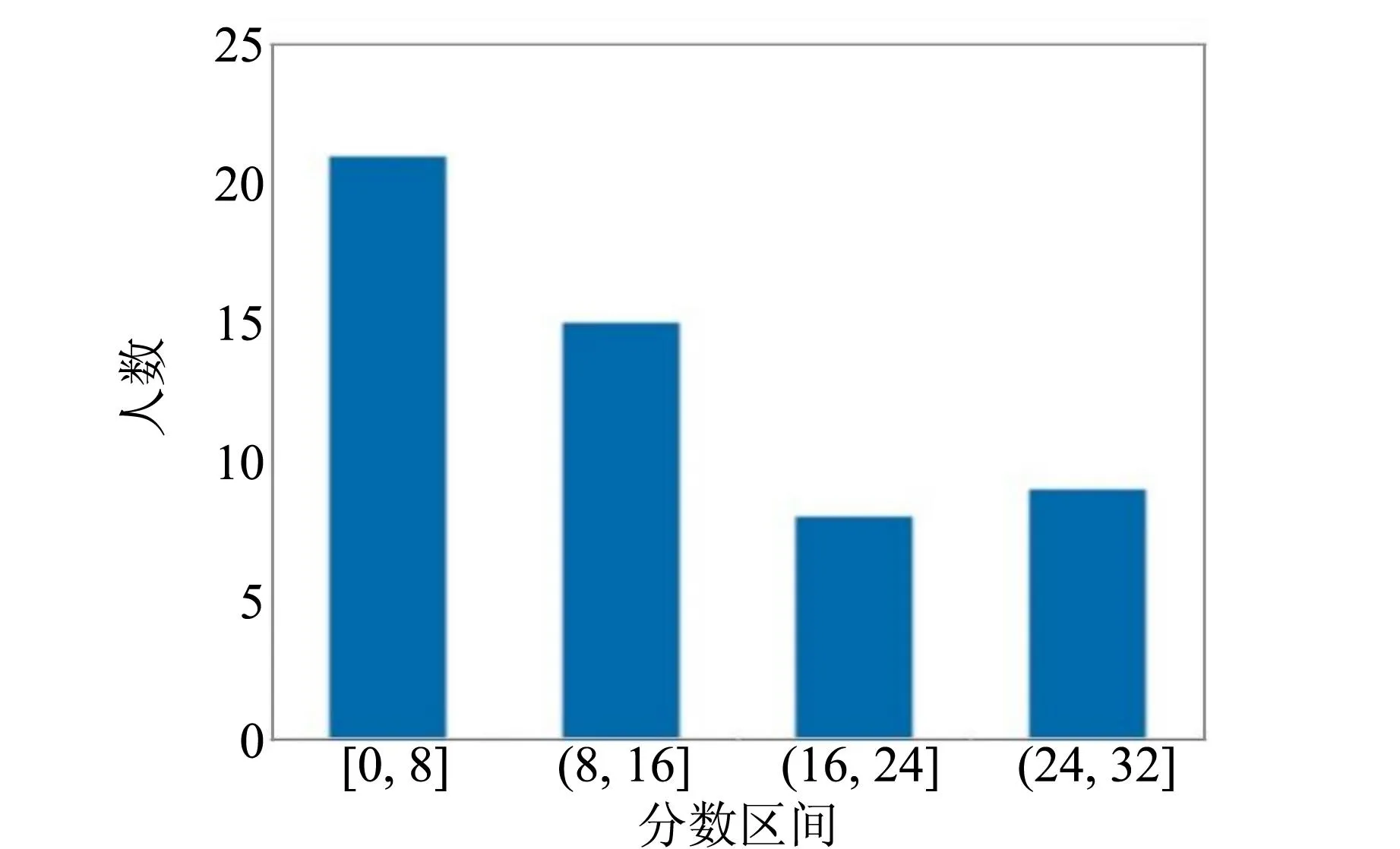
图6 题目1)答题情况统计表
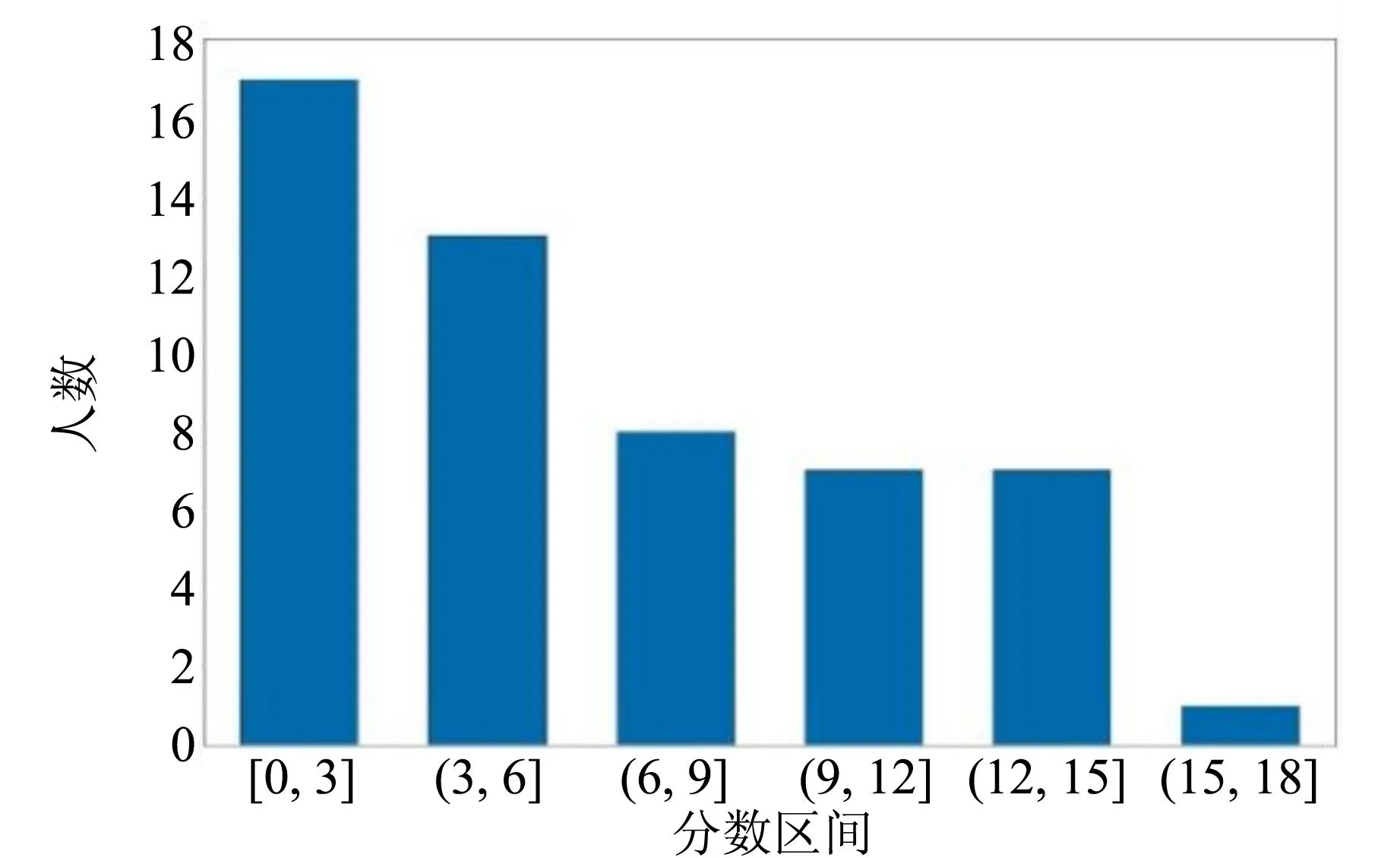
图7 题目2)答题情况统计表
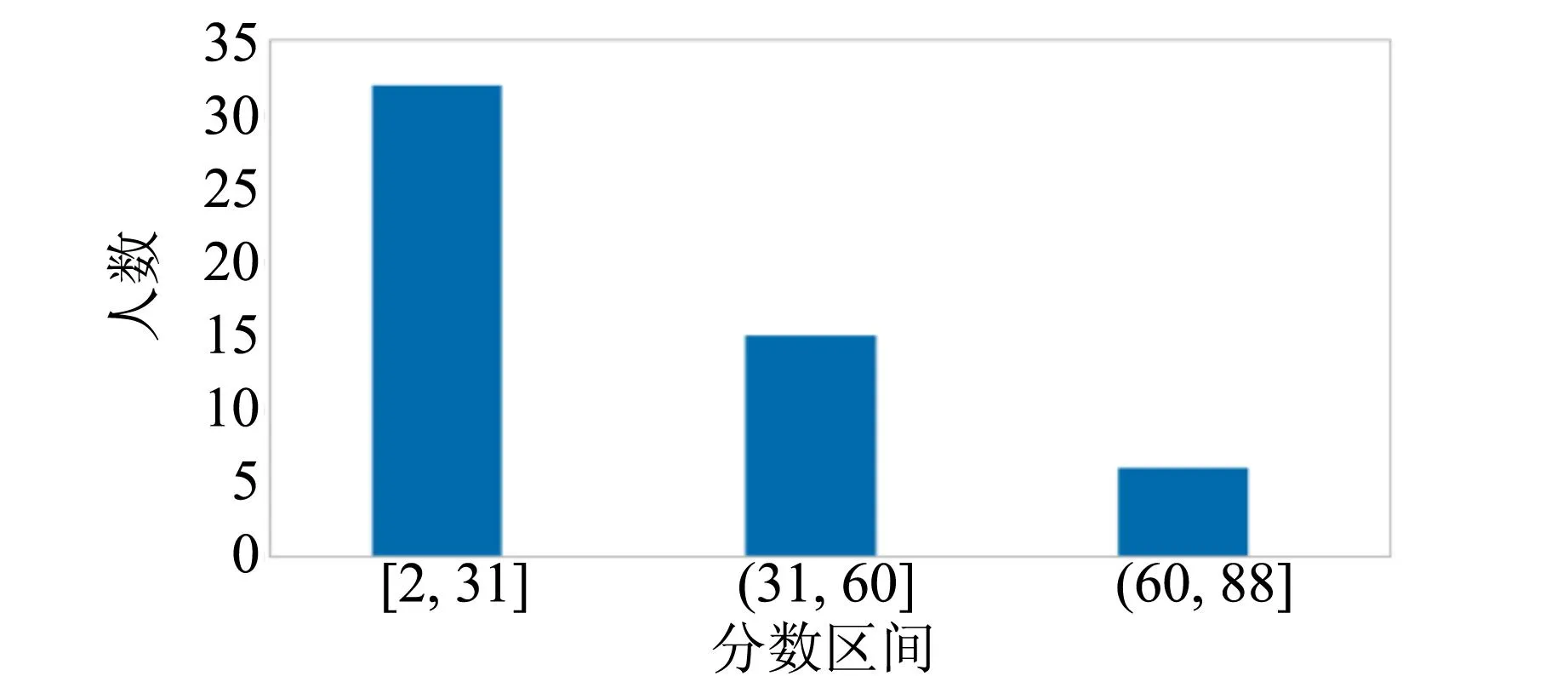
图8 考生总得分情况统计表
接近1/3的学生能在题目1)中得到50%以上的分数,得分区间从低到高,人数大体呈递减趋势,从实验过程和答卷结果看,能够熟练掌握分光计使用的学生占少部分. 大部分学生能够写出题目2的实验方案,但在方案的设计依据、可操作性上没能很好地解释,导致大部分学生的得分偏低,说明学生对折射率、色散等知识点的掌握较弱.
由于大部分学生在前2项实验内容上花费的时间较长,且无法得出正确的结果,导致后面的问题开始出现较大的区别,只有少部分学生能够完成后续实验内容. 在数据拟合及误差分析部分,大部分学生的得分主要来自于对拟合方法及误差来源的定性分析,这与赛前的预期存在较大偏差. 这可能是源于近年的教学中,学生倾向于使用电脑中的Origin, Python和Matlab等工具做误差分析和公式拟合,少有学生会训练使用计算器和最小二乘法手动计算拟合公式以及做误差传递练习. 建议在以后的比赛中,可以考虑给选手们配备计算机和常用数据处理软件来做数据分析.
4.2 数据比对
本次竞赛题目在赛前由出题教师、实验技术人员及本学院优秀研究生对32套实验设备和样品各进行8次完整实验,实验平均用时2 h;为评估难度,邀请本学院已完成基础物理实验课程的优秀本科生试做5次,平均每次用时2.5 h,实验结果皆在参考值范围内.
通过汇总试卷的答题情况,除去数据空白的考卷样本,对考生测出数据与考前测试得出参考数据进行对比,结果如表4~6所示.

表4 测得汞灯中5条发射线数据比对

表5 测得三棱镜的折射率数据比对

表6 测得未知液体的折射率数据比对
在监考过程中,也对学生的实验进度做了相关统计,实验待测元件主要是光栅、三棱镜和未知液体,学生依次按顺序测量,每隔30 min记录学生操作进度如表7所示.
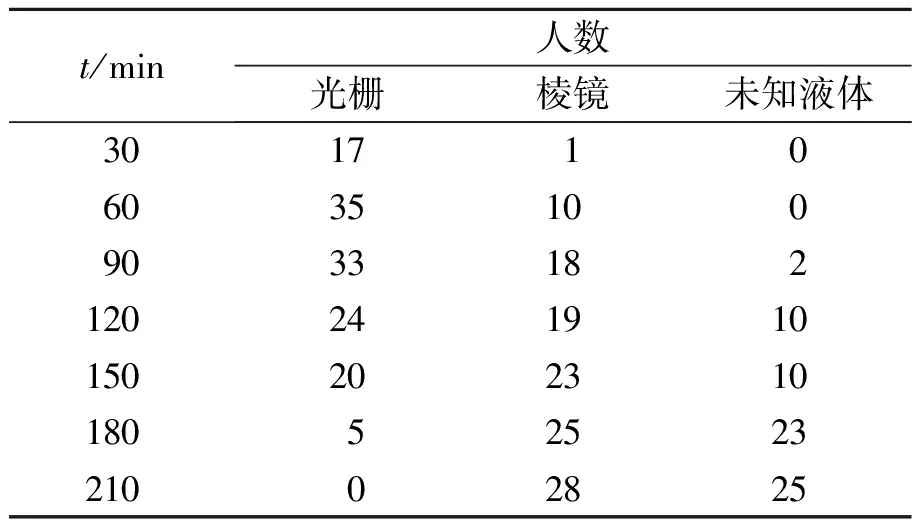
表7 学生操作进度表
从统计数据中看出,大部分学生能在2 h内完成仪器水平调节,测量出光栅常量,但要完全完成本题基本测量内容,测量出棱镜折射率需多花费1 h时间. 从考场的实际情况来看,选手们操作部分的主要问题在于不善于利用学过的理论知识来指导实验操作. 部分选手因为在实验课或光学理论课上学过最小偏折角测量方法,会凭借模糊记忆转动待测物品和望远镜,花费大量时间寻找出射光线. 尤其是当加入液体后,偏折角会大幅度变小,若选手仍在之前的偏折角范围附近寻找出射光线,则会无功而返. 正确的做法是先制定实验方案,通过绘制简单的光路图,快速估算出最小偏折角的大概范围,然后再调节待测样品和望远镜的摆放方位,寻找出射光线.
本次竞赛基础题B在重点考察的第1),2),4)题中分别设置了锦囊1,锦囊2,锦囊3,共有12名考生领取了锦囊1,4名考生领取了锦囊2,1名考生领取了锦囊3. 比赛规定,锦囊1在开考1 h之后可以使用,并扣减对应考题得分分值15分(扣到0分为止,以下同),锦囊2在开考2 h之后可以使用并扣减对应考题得分分值15分,锦囊3在开考3 h之后可以使用并扣减对应考题得分分值4分. 约23%的考生领取了锦囊1,但是锦囊2只有不到8%的同学领取. 事后分析,可能因为考生们觉得领取锦囊2,总分值20分要扣15分不太“划算”,但是领取锦囊1的话则是总分值30分扣15分,相对“划算”. 锦囊3则因为大部分考生在比赛中未能做到第四小题部分,几乎无人领取.
4.3 竞赛题目和教学题目的对比
在大学物理实验教学中,使用分光计和最小偏折角原理测量三棱镜的折射率是比较常见的实验. 为了让参赛学生不重复太多课堂上做过的实验,同时体现竞赛的深度,命题小组成员对教材上的题目做了以下变动:
1)增加了光栅和钠光灯,考察学生使用光栅方程测量未知谱线波长的能力.
2)使用教学分光计来测量三棱镜顶角的不确定度大小一般在几个角分. 在本实验中,为了节约学生的操作时间,移除了三棱镜顶角测量的操作部分,转而要求学生使用固定的顶角值60°来做计算. 该要求会给后续所有折射率的测量带来额外的不确定度,大小估算为0.001.
3)误差分析部分,为节约学生时间,并未要求学生使用多次测量的实验数据来做误差分析,而是做了大幅度的简化,让学生直接使用假设的测量误差来推算500 nm波长下折射率n的误差. 该题目可以考查学生对使用蒙特卡罗法或者误差传递法分析测量误差的掌握程度.
5 调查问卷统计
共回收到40名参赛选手问卷,其中物理类学生29名,非物理类学生11名,统计结果如表8所示. 选手反映的问题主要集中在理论知识没掌握. 不习惯方案撰写及物理建模有困难等3方面,可以理解为在日常实验教学模式中,学生已习惯教师提供资料,学生根据资料进行实验操作,并根据资料进行问答式的数据分析及问题回答,这导致学生独立思考的空间小,扩展能力不足. 对于本赛题的改进建议,主要集中在“提供更多的背景知识和解释”,本赛题是基于大学物理常规实验分光计实验进行提升,平行扩展,对此可以理解为学生对于基础理论知识的掌握不够扎实,在遇到新事物时无法举一反三地使用学过的知识.

表8 调查问卷统计分析
对比竞赛成绩与调查问卷结果,可以看出学生在光学实验中存在以下几方面薄弱点:
1)理论知识掌握不够透彻,对于光的色散、折射的理解层次较浅,当遇到复杂系统时,无法调用基础理论进行实验拓展;
2)高阶层次实验设计能力训练不足,日常实验教学中,学生较习惯由教师提供讲义及实验报告模板,学生按照教师思路按部就班地做实验,学生发现问题,独立思考解决问题的能力较为薄弱;
3)光学具象建模能力弱,若光学实验中使用了导轨,把光轴限定在一维平面时,学生能较轻松地完成实验,而一旦实验光轴扩充到二维平面,学生就需要花费大量时间在“盲猜”中寻找想要的光学现象,从本次竞赛中学生利用最小偏折角方法时的表现也体现出这一点;
4)数据处理能力有待加强.
如何改进以上学生实验学习中的薄弱点,可以作为后续实验教学改革的探索方向,从而培养出基础扎实,具有良好创新能力和科研素养的基础研究人才.
6 结束语
本次竞赛内容从基础光学实验分光计的调节与使用出发,既检验了学生对于光栅和三棱镜等分光元器件的操作使用本领,又考查了学生对光栅方程和最小偏折角原理等理论知识的运用. 相较于传统的课堂实验项目,通过加入未知液体折射率的测量,提升了实验难度,进一步考查了选手“举一反三”的实验方案设计能力. 实验竞赛现场没有配备电脑,对选手的实验数据分析和拟合带来一定影响,未来可考虑通过加大比赛投入来改善. 竞赛结果表明,在未来的物理实验教学中应当思考如何更有效地培养学生的实践能力和综合素养,并能将所学知识应用于实际问题的解决.
感谢何振辉教授对题目设计提出大量宝贵建议,以及对赛后论文撰写的悉心指导!
