一种基于图像的燃气轮机叶型参数测量方法
2024-03-05崔则阳孔祥玲付经伦施佳君
崔则阳,孔祥玲,付经伦,施佳君
(1.中国科学院工程热物理研究所先进燃气轮机实验室,北京市 海淀区 100190;2.中科南京未来能源系统研究院燃气轮机数字化中心,江苏省 南京市 210000;3.中国科学院大学,北京市 海淀区 100000;4.中国科学院大学南京学院,江苏省 南京市 210000)
0 引言
以燃气轮机为代表的叶轮机械是能源动力领域的重要设备,是大电网发电和调峰的最佳选择,在国家能源安全中扮演着无可替代的角色,是关系到国民经济发展的高端核心装备[1-7]。叶片是叶轮机械的关键零件,是实现工质能量转换的重要载体,其造型质量直接影响叶轮机械工作效率和性能。叶片加工过程复杂,精度要求高,必须通过精确的测量手段进行误差评定,以保证叶片制造质量[8-9]。另外,叶片制造通常采用批量生产,且种类繁多,需要快捷高效的检测方式。
当前国内常用的测量方法分为接触式和非接触式。其中,接触式测量包括标准样板测量、电感量仪测量、三坐标测量机测量,非接触式测量包括激光测量和机器视觉测量。标准样板法[10]操作简单、成本低,适用于生产现场,但是测量精度和自动化程度低,需要大量的标准样板进行匹配。电感量仪[10]采用传感器感应截面坐标信息,测量精度较高,环境要求低,但是成本高、通用性差,需要利用标准叶片对仪器进行校准。三坐标测量机[10-12]选用高精度测头获取叶片轮廓坐标值,测量精度高,但是测量效率低、价格昂贵,需要专业的测量场所。以光学测量为主的非接触测量具有自动化程度高、测量效率高的特点。激光[13]和机器视觉[14]测量是目前2种主要方式,二者相比,激光测量设备成本和对操作人员的要求都比较高;机器视觉测量操作简单、成本低,是实现叶片快速测量的理想方法。
本文提出的基于图像的叶型几何参数测量方法以计算机视觉为基础[15],操作简单且测量精度较高,可广泛应用于叶片检测中。
1 基于图像的叶型参数测量方法
1.1 基于图像的叶型参数测量方法步骤
基于图像的叶型参数测量方法由图像获取、图像预处理、叶型参数初步识别及准确获取4个步骤组成,如图1所示。

图1 基于图像的叶型参数测量方法步骤Fig.1 Steps of the proposed image-based blade parameter inspection method
1.2 叶型图像获取
叶型图像的获取需要综合考虑测量精度和运算效率的要求。假设叶型参数的测量精度要求为λ,所选相机的图像分辨率为u×v,其单位像素pi在目标视距d的图像测量精度σ由计算得出,其中视距d为目标到相机的距离。
若σ≤λ,那么所选相机是合适的;若σ>λ,则需要选用具有更高分辨率的相机。在一定视距下,测量精度要求越高,图像所需的分辨率越高、运算时间越长。
1.3 叶型图像预处理
为了获取高质量的叶型图像,在进行参数测量之前需对图像进行预处理,具体包括噪声处理和特征增强,以分辨率u×v的图像为例进行说明。原始图像表示为f0(i,j),其中(i,j)为图像f0中第i行第j列像素点的坐标。采用高斯滤波器[16-17]G(i,j)进行图像噪声处理,降噪后的图像fG(i,j)通过式(2)对边缘进行增强,以获得准确、清晰的叶型图像f(i,j)[13]。
式中a和b分别为对比度调节因子和亮度调节因子,本文取a=1.2,b=30。
1.4 叶型参数测量
1.4.1 叶型轮廓提取
叶型轮廓的准确提取是叶型参数精确测量的重要保证。本文首先采用Canny算子[18]对叶片图像内的边缘信息进行提取。通过应用形态学图像处理方法[19]的腐蚀和膨胀操作,对边缘提取后的孔洞进行填充[20-22],以获得叶片图像中所有的边缘信息。之后,采用最大外缘轮廓法[23-24]对已提取出的所有边缘信息进行筛选,最终获得叶片外形轮廓信息,记为fc,且fc∊Rm×2,其中m为轮廓点的总数。
本文采用的最大外缘轮廓法的具体实施方法为:假设经过形态学图像处理后的叶片图像为f(i,j),定义f(i,j)中目标叶型及背景所在区域的像素值分别为1和0。最大外缘轮廓法采用图2所示的3×3窗口对f(i,j)进行扫描,根据像素点(i,j)和其邻域的8个像素点N8(i,j)内的值对轮廓进行提取。
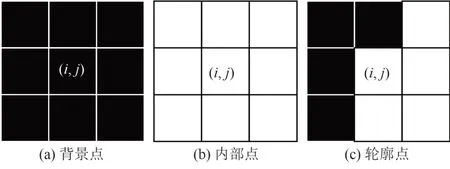
图2 背景点、内部点和轮廓点定义Fig.2 Definitions of background point, internal point and contour point
若像素点(i,j)和其邻域的8个像素点N8(i,j)的值均为0,则判断像素点(i,j)为背景点,如图2(a)所示。反之,则判断像素点(i,j)为内部点,如图2(b)所示。若像素点(i,j)和其邻域8个像素点N8(i,j)内的值既有1也有0时,则判读像素点(i,j)为轮廓点,如图2(c)所示。
1.4.2 测量参照物选择
以10 mm×10 mm大小的正方形作为尺寸参考,通过正方形在图像中所占的像素数,计算出单位像素的长度,从而推算出叶型关键参数。
1.4.3 叶型参数定义
叶型参数[25]如图3所示,定义轴线方向为x轴,额线方向为y轴。图3中,Of(Of,x,Of,y)和Or(Or,x,Or,y)分别为叶片前、后缘圆心;Rf和Rr分别为前、后缘圆弧半径;L为前、后缘圆心间的x轴向距离。叶片中弧线记为αf和αr分别为中弧线在入口边和出口边切向与x轴的夹角,记为几何入口角和几何出口角;Omax,Rmax分别为叶型最大厚度处圆弧圆心和半径;Pmax为前缘圆心Of到Omax的x轴向距离;T为中弧线极大y值点位置;Tmax为前缘圆心与T间的x轴向距离。

图3 叶片叶型参数Fig.3 Feature parameters of the blade
1.4.4 叶型参数初步识别
叶型参数测量的第一步是采用骨架提取的方法确定叶片的中弧线令S(A)表示C(x)上点的集合,以不同半径的圆形结构Bi对叶型图片进行腐蚀和开的运算,如图4所示。

图4 基于图像的叶片叶型关键参数测量软件界面Fig.4 Software interface of the proposed image-based blade feature parameter inspection method

图4 叶片骨架提取Fig.4 Skeleton extraction for a blade image
式中:k为迭代次数;符号“⊖”和“◦”分别表示腐蚀和开运算。最大迭代次数K为
那么,叶片中弧线上的点S(A)表示为
S(A)两端点为叶片前、后缘圆心Of和Or,L可由式(6)计算得到:
式中Of,x和Or,x分别为前、后缘圆心的x轴坐标。
采用三次曲线对S(A)进行拟合,则中弧线方程可表示为
式中:x∊[0,L];a0,a1,a2为系数。方程式(7)求解需满足以下约束条件:
其中,αf和αr的表达式为
将式(8)和式(9)代入式(7),求解得
中弧线极大值点位置T为=0处。前缘圆心Of到中弧线极大值点位置T的轴向距离Tmax由式(11)计算获得
叶型厚度分布函数R(x)采用三次曲线控制:
式中b0,b1,b2,b3为常数。R(x)满足以下约束条件:
令fc,k∊fc,k∊[1,m],(xk,yk)为fc第k个点的坐标,则Rf,Rr,Rmax的表达式[26]为
由式(13)、(14)可求得
最大厚度处圆弧圆心坐标表示为
Pmax表示为
1.5 叶型参数准确获取
叶型中弧线C、前后缘圆心x轴向间距L、最大厚度位置Omax及半径Rmax,前、后缘位置Of,Or及半径Rf,Rr,几何进、出口角度αf,αr等参数决定了叶片形状。令H(i,j)为由叶片参数P确定的叶型,其中P的表达式为
叶型参数准确获取的目的是寻找一组参数P,使得由P确定的叶型H与由图像提取出的叶型轮廓fc重合,那么叶型参数准确测量过程可描述为
式中初始叶型H0为由参数P0确定的叶型,精确的叶型参数采用列文伯格-马夸尔特(Levenberg-Marquardt,LM)算法[27]迭代求解。
2 测试验证
2.1 测试环境介绍
以上基于图像的叶型参数测量方法采用Python 3.85在Pycharm Community 2021.1中编译,并开发了基于图像的参数测量软件(登记号2020SR1770966),集成叶片图像预处理,叶型参数测量和参数检测功能。软件界面如图4所示。
对该软件进行叶型参数测试应用。通过相机采集到的图像分辨率为4 032×3 024,相机水平置于固定支架上,如图5所示,相机距离被测物的高度为380 mm。

图5 图像采集环境Fig.5 Experimental setting for image acquisition
以某型透平叶片的打印图为测量对象,其主要几何参数如表1所示。在被测对象上侧放置10 mm×10 mm正方形块为尺寸参照物。

表1 某型叶片叶型关键参数Tab.1 Feature parameters of a blade
2.2 叶型图像预处理
采用图像预处理程序对目标区域进行截取,截取后图像分辨率为1 056×780。采用大小为5×5,标准差为0的高斯滤波器对图像进行处理。经过图像预处理后的结果如图6(b)所示。

图6 叶型图像预处理Fig.6 Preprocessing for the turbine blade image
2.3 叶型参数初步识别
以前缘圆心Of为坐标原点。表2给出采用1.3.4所述方法提取的叶型关键参数。可见,初步测量的最大误差分别为前后缘圆心间x轴距离L,最大厚度Pmax和几何入口角αr。对比基于测量参数重建叶型和原始叶型(如图7所示),重建叶型有较大误差,需要对测量值进行精确求解。
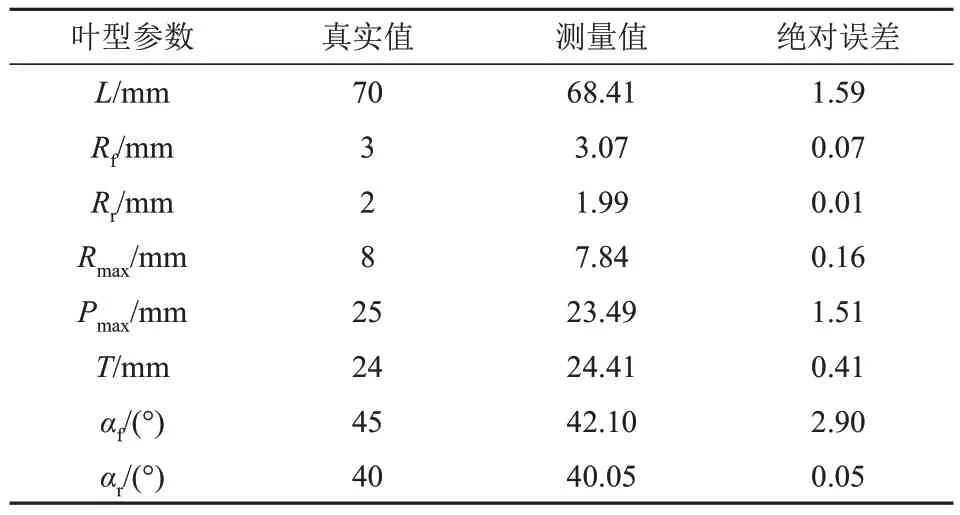
表2 叶型参数测量结果与真实值误差分析Tab.2 Error analysis between the inspected feature parameters and the standard values

图7 基于测量值重建叶型与原图叶型对比Fig.7 Comparison between the original and the turbine blade reconstruction using inspected feature parameters
2.4 叶型参数准确获取
采用LM算法对测量值进行优化,最大迭代数和残差分别设定为n≥1 400和ε≤e-6。优化过程中的残差曲线如图8所示,优化结果如表3所示。
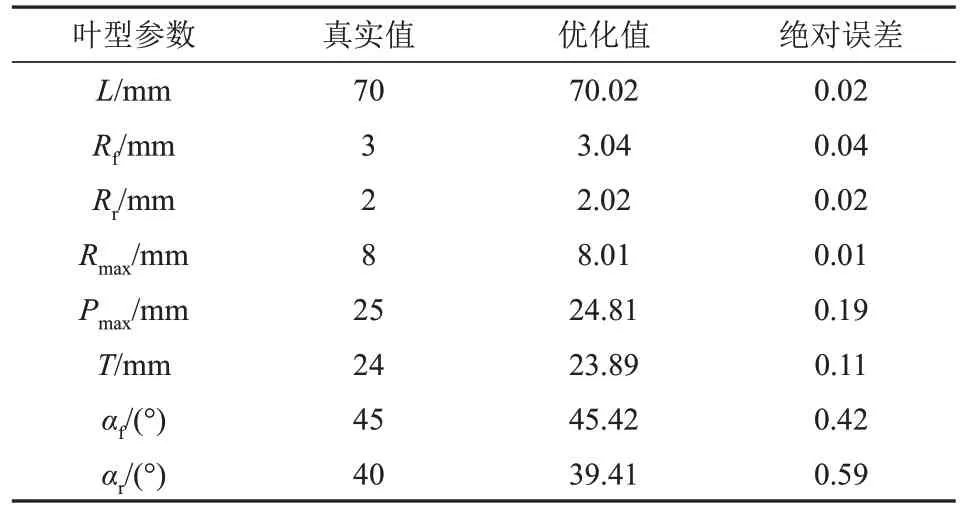
表3 叶型参数优化结果与真实值误差分析Tab.3 Error analysis between the optimized feature parameters and the standard values

图8 参数优化过程收敛性Fig.8 Convergence of the feature parameter optimization
优化后,测量参数最大误差为δ(Pmax)=0.19 mm,最大角度误差为δ(αr)=59°。图9对比了根据最终测量结果重建的叶型与原始叶型,二者吻合效果良好。由于测量精度与图像分辨率有直接关系,通过增大图像分辨率,将进一步提高叶型参数测量精度。
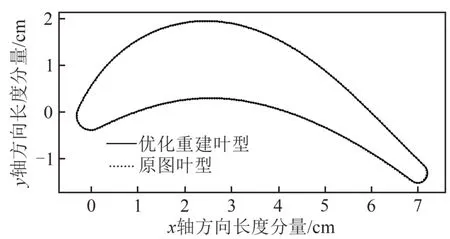
图9 基于优化值重建叶型与原图叶型对比Fig.9 Comparison between the original and the turbine blade reconstruction using optimized feature parameters
3 结论
提出了一种基于图像的透平叶片叶型关键参数优化测量方法。该方法可实现透平叶片叶型关键参数的非接触式测量。实验表明,该方法具有较高的测量精度,测量绝对误差不大于±0.2 mm,相对误差不大于1.5%。开发的软件及测量方法具有自动化、流程化和智能化的特点,可应用于工业叶片的批量生产和检测。
