基于边缘计算的融合多因素的个性化推荐算法

金焕章，朱容波，刘浩，陈慧敏

（中南民族大学 计算机科学学院，武汉 430074）

随着物联网技术飞速发展、用户规模快速增加、移动边缘设备的不断普及、用户需求变得多样性，在海量数据中准确获取感兴趣的内容变得更加困难［1-3］.如果没有及时动态感知用户偏好的变化，会很大程度上降低用户的体验感，因此及时且准确地推荐用户感兴趣的内容具有巨大的应用价值［4］.

为了提高在复杂多样数据下的推荐精确度，现有工作主要集中在解决稀疏数据情况、冷启动和对属性潜在关联的提取问题上［5-6］.比如：ZHAO 等［7］提出了基于多因素聚类的协同过滤推荐算法，使用Kmeans 和差分聚类算法对用户进行分组，根据用户属性和项目属性构建邻接矩阵，稀疏情况下也有不错的推荐效果.考虑到数据稀疏和过拟合对推荐系统的影响，LUMAUAG 等［8］提出了一种改进的协同过滤推荐算法，以解决数据稀疏和过拟合问题.KOREN 等［9］将用户物品评分矩阵分解成用户矩阵和物品矩阵，可以挖掘出用户和物品的潜在关联.文献［10］提出了一种协同奇异值分解模型，考虑了用户偏好随时间的变化和标签与项目之间的相关性，在处理稀疏数据和过拟合问题上取得了不错的效果.该方法综合考虑了多因素，导致算法的时间过高.为了解决数据过载、计算速度慢等问题，采用一种新的预训练任务和框架［11］，把Masked language model 预训练改用判别式的Replaced token detection代替，减少了预训练的时间.然而，现有推荐算法大多采用集中处理模式，无法很好地处理当前网络边缘设备爆炸式增长的数据.集中式推荐系统通过云服务器响应用户的请求，然而云服务器的算力限制和传输时延使得其无法及时感知用户偏好的变化，无法提供更为精确的个性化推荐.

边缘计算为推荐算法的设计注入了新的活力.边缘计算能够将数据转移到网络边缘设备，节省网络带宽、降低延迟、提高数据的安全性［12］，并有效解决响应速度和信息过载等问题.LIN 等［13］将定位器和身份信息整合到边缘设备中，使用固定身份映射预测算法，解决更新的延迟.考虑安全问题，文献［14］提出了隐私保护的检索框架，将每个边缘节点建模成一个分布式的上下文动态处理过程.LI 等［15］研究了下一个新的边缘计算节点隐私保护问题，通过加权噪声注入方法来保护用户的位置信息，基于Forward算法预测用户的下一步动作，具有更好的隐私保护和推荐精确度.考虑到多个边缘节点的关联，KONG 等［16］提出了基于交互行为的边缘节点信任评估机制，在边缘节点之间建立信任关系，通过时间衰减的多源信任融合算法进行聚合，提高了计算效率.文献［17］在边缘计算中运用模糊聚类降噪自编码和重组嵌入网络技术，研究如何更好地利用上下文信息，减少了过拟合问题.

然而，现有研究集中在根据单一的上下文信息构建模型，但是面对大数据，存在数据稀疏、数据特征提取难、冷启动等问题，很难做到个性化推荐.为了解决上述问题，本文提出了基于边缘计算的融合多因素的个性化推荐算法F-SVD，在边缘服务器通过F-PEARSON 计算用户之间的相似度，运用BERT模型训练个人偏好，并上传至云服务器，在云服务器使用F-SVD 计算用户与用户、用户与项目之间的潜在关联特征，并进行预测.

1 基于边缘计算的融合多因素的个性化推荐算法F-SVD

1.1 问题描述

由于物联网行业的快速发展，伴随着5G普及和带宽增加给云服务器带来了巨大的压力，如何在海量数据中给用户精准推荐感兴趣的内容变得困难许多.传统推荐算法大多是基于集中式计算，无法做到随着用户偏好的变化及时调整推荐内容.用户通过手机、电脑、平板和车联网产生数据（itemId、userId、rating、genres、timestamp、tags）、边缘服务器进行个性化计算（Su、μk）、云服务器挖掘用户之间的潜在关联.系统模型如图1所示.本文涉及的符号如表1所示.

表1 符号表Tab.1 Symbol table

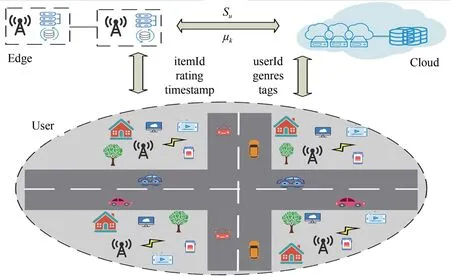
图1 系统模型图Fig.1 System model diagram

在边缘服务器进行数据的个性化计算，包括运用F-PEARSON 计算用户之间的相似性得分Su并排序，采用BERT模型训练数据计算前k位用户对某个年代某种类型项目的平均评分μk.在云服务器，计算用户与用户、用户与项目之间的潜在关联特征，根据F-SVD 算法计算当前用户对物品的预测评分r̂(u，i).目标函数如公式（1）所示：

1.2 F-PEARSON

提出了一种新的用户相似度计算方法FPEARSON，该算法在边缘服务器执行，输入为项目id、用户id、评分、评分时间戳，输出为用户之间的相似度得分，并上传至云服务器.在传统的皮尔森相关系数基础上考虑到两个用户对项目评分的平均值，若用户评分的平均值越接近那么认为用户越相似，定义如式（2）：

式中：a(u1，u2)表示用户关于平均评分的相似度，ṙu1表示用户u1对所有项目评分的平均值，ṙu2表示用户u2对所有项目评分的平均值，χ表示调整超参数.

若用户之间共同评分的项目越多代表用户的兴趣更接近，其中包括共同评分项目的数量、共同评分项目的评分值，定义如下：

式中：c(u1，u2)表示用户在共同评分项目上的关联度，r(u1，i)表示用户u1 对项目i的评分，r(u2，i)表示用户u2对项目i的评分，ṙu1表示用户u1的平均评分，ṙu2表示用户u2的平均评分.

考虑到两个用户评分项目的频率，评分频率越接近那么它们更相似，对计算到的用户评分频率进行归一化处理.

式中：f(u1，u2)表示用户关于评分频率的相似度，t(u1，tmax)表示用户u1 最近一次评分项目的时间戳，t(u1，tmin)表示用户u1 最早一次评分的时间戳，t(u2，tmax)表示用户u2 最近一次评分的时间戳，t(u2，tmin)表示用户u2 最早一次评分的时间戳，γ表示调整超参数.

综合以上因素，最终用户的相似度计算公式为：

1.3 基于机器学习的BERT模型特征训练

在边缘服务器运用BERT 模型进行无监督训练，输入为项目id、项目类型、用户id、用户评分、时间戳，输出为用户对项目的预测评分，在此任务里，通过在具有上下文关系的句子里加入一些特殊的token，在句子开始标志［CLS］，两句话的中间位置标志［SEP］.比如语料库里有两句话：［CLS］用户1 对90 年代Comedy 类型的项目［SEP］评分为5［SEP］具有上下文关系，另外一句为［CLS］用户1 对90 年代Comedy 类型的项目［SEP］武汉疫情［SEP］，没有上下文关系.也就是说句子A 和B 作为预训练样本，B有一半的可能是A的下一句，属于上下文关系，也有一半的可能是随机句子，不属于上下文关系.

通过BERT 模型训练数据进行预测，然后取最相似的k位用户的均值μk作为当前预测的基数.rui为用户对某个年代某种类型项目的评分，定义如下：

1.4 F-SVD

为了解决传统推荐算法使用评分、标签、时间或单一的上下文信息进行推荐，在海量数据中很难挖掘潜在特征信息，难以做到较好推荐，提出了一种基于边缘计算的融合多因素的个性化推荐算法F-SVD.F-SVD 算法本质就是融合考虑用户与用户、用户与项目之间的多属性信息，包括用户的评分、评分频率、标签爱好、对不同年代电影偏好等信息，能够更好地挖掘出潜在关联信息，从而构建更完善的模型，非常适合当前多元化的网络环境.F-SVD 算法如表2所示.

表2 F-SVD算法Tab.2 F-SVD algorithm

在云服务器中F-SVD 算法接收来自边缘服务器的数据，其中包括用户之间的相似度和用户对项目的预测评分.算法具体步骤为：

首先，初始化数据并将数据分为训练集、测试集和验证集.运用F-PEARSON 计算用户之间的相似度得分su并排序.采用BERT 模型训练历史数据，得到用户对某个年代某种类型项目的评分.根据用户对项目的评分数据集转为用户对项目的评分矩阵R.根据矩阵R和特征维度D 转为用户特征矩阵U和项目特征矩阵V.

分类：用户对不同类型项目的喜好程度是不一样的，将项目分成犯罪、战争、爱情、科幻等19类，分别用1～19 标识.遍历用户所有评分的项目，统计每类项目的总评分和对应的项目数量，求出用户在不同类型项目中的平均评分.

用户喜欢项目的类型不一样，通过计算用户使用标签t1的次数和用户使用过的标签总数，计算用户在打此标签的项目评分和当前用户所有项目评分的差值，若当前项目的评分高于平均评分则在预测的时候加上该差值，反之减去该差值.定义如下：

式中：l(u，t1)表示标签对用户评分的影响，w(u，t1)表示用户u使用标签t1所占的权重，t1 ∈r(u，t)表示用户u使用过的t1标签，r(u，i)表示用户u对项目i的评分.

考虑用户对不同类型的项目会打出不同的评分，计算出用户在此类型项目上的评分比上用户对所有项目评分的均值作为用户对不同类型项目评分的偏差.定义如下：

式中：w(u，g)表示在用户u当中类型为g的项目所占的比重，rˉ(u，g)表示用户对类型为g的项目的平均评分.

如果用户喜欢某种类型的项目那么评分的频率会更高，计算用户最近两次评分同种类型项目的时间差，差值越小代表用户越喜欢此类项目，由于用户两次评分的时间戳差值比较大，进行了归一化处理，定义如下：

式中：t(u，t)表示时间t对用户u的影响，f(u，i)表示当前类型项目对用户评分项目总数的占比，β表示调整超参数.

最终融合多因素的预测评分公式定义如下：

式中：k表示与用户最相似的前k位用户，ur表示前k位用户的平均评分的偏差，bu表示用户的评分偏差，bi表示项目的评分偏差.Uu和Vi表示潜在因子矩阵U的第u行和矩阵V的第i行.

最终的目标函数如公式（1）所示：其中为预测的评分，r(u，i)为真实评分，‖U‖，‖V‖分别表示用户特征和项目特征的正则项，λ为正则化参数，通过网格搜索确定，bu表示用户的评分偏差，bi表示项目的评分偏差.在目标函数中分别对ur、bu、bi、Uu、Vi求偏导，如公式（11）所示.运用随机梯度下降法进行求解，使得目标函数下降最快.每一次循环后计算预测值和真实值的误差，并更新矩阵里面的值，如果达到最大迭代次数或者误差小于给定的阀值则跳出循环.

1.5 性能分析

根据具体的算法代码计算，设m为被评分的总数，n为评分的用户总数，p为项目总数，q为标签总数.对F-SVD 算法的时间复杂度分析如下：第1 步，对所有的评分项目进行分类，此时需要遍历所有的评分项目，时间复杂度为O(mp)；第2 步，计算用户在不同类型项目中的评分均值，此时时间复杂度为O(mn)，获取项目类型的时间复杂度为O(1)；第3步，计算用户打标签偏好的时候需要遍历所有的标签次数，此时时间复杂度都为 O(mq).因此，F-SVD 算法的时间复杂度为：O(mp) + O(mn) + O(mq).

2 实验结果和分析

2.1 实验配置

为了验证所提方法的优越性，采用了电影推荐算法领域最权威的公开数据集MovieLens-small（http：//grouplens.org/datasets/），其中包含了100004条评分数据、9125 部电影、671 个用户、1056 个用户标签、时间、类型等属性.选取80%的数据作为训练集，10%的作为测试集，10%作为验证集.由于条件的限制，选择自己笔记本模拟为边缘服务器，实验室服务器为云服务器，给出了操作系统、内存、处理器、语言、工具等信息，具体实验环境配置如表3所示.

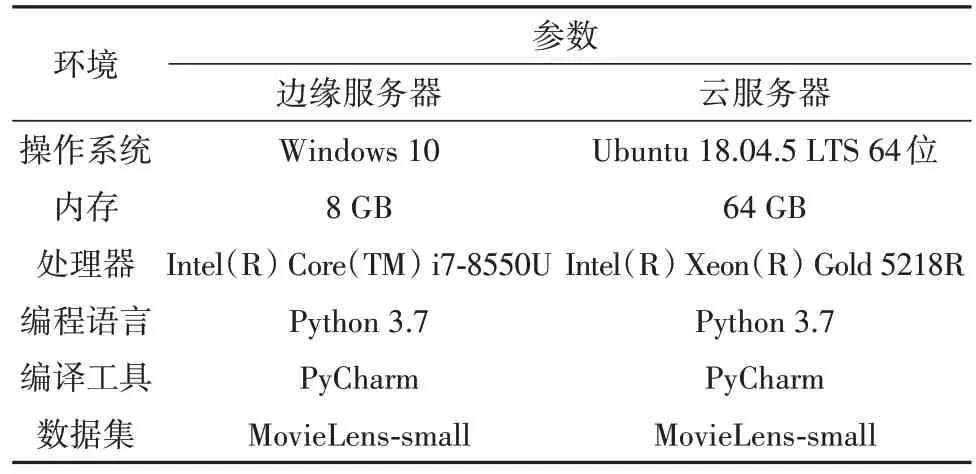
表3 实验环境Tab.3 Experimental environment

2.2 评价指标

为了合理验证本文提出的F-SVD 算法的效果，从以下评价指标进行验证：RMSE 均方根误差表示预测评分和实际评分的误差；MAE 平均绝对误差表示预测结果的实际误差情况；PRECISION 精确率表示用户感兴趣的产品包含在推荐列表中的比例：

实验包括：（1）确定参数对F-PEARSON 和FSVD 算法的影响；（2）将提出的F-SVD 算法和EnhancedCF、RSVD、Co-SVD 算法在RMSE、MAE 和PRECISION 上进行对比.在F-SVD 算法中加入基于机器学习的BERT 模型与Word2Vec 和AutoEncoder的对比实验.

2.3 参数对算法性能的影响

在边缘服务器中，为了确定χ参数和γ参数对F-PEARSON 相关系数的影响，分别做了20 组实验来确定χ的值和γ的值，确保取到可靠的参数.

图2 为不同χ值在RMSE 和MAE 上的实验结果图.随着χ参数的增大，误差曲线从0 到0.05 有下降趋势，之后一直呈上升的趋势，χ= 0.05 时，此时RMSE=0.73398，MAE=0.53577.在0.05 到0.15 期间，误差变化最快，随后误差呈平稳缓慢上升.根据公式a(u1，u2)= exp (-χ|rˉu1-rˉu2|)，该指数函数单调递减，χ值越大该值越小，对相似性的影响就越低.在计算相似性时是加上该函数的值，如果函数值太小，对相似性的影响几乎可以忽略，那么χ值应该在（0，1）内取.通过反复试验，最后发现当χ=0.05 时RMSE和MAE误差均为最小.

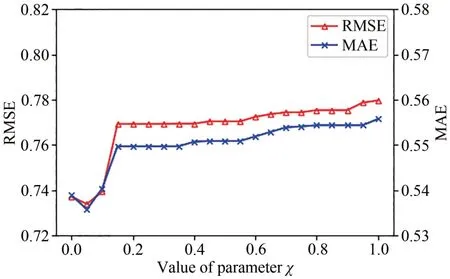
图2 χ值对误差影响Fig. 2 Impact of parameter χ on error

图3 为不同γ值在RMSE 和MAE 上的实验结果图，有图3 可见：0 到0.02 过程中RMSE 和MAE 误差趋于下降，然后出现快速上升，之后趋于平稳.由于数据稀疏性，用户评价电影的频率可能有很大的不同，因此对用户的评分电影频率进行归一化处理，保证归一化后的值都为正数.同样地该指数函数单调递减，随着变量取值的增大其函数值越小，则对相关性的影响就越弱.归一化后用户的评分电影频率相差绝大多数比1 大，而e 的负1 次方约为0.368，而e的负2次方约为0.135，下降的速度很快，所以应该尽量的缩少变量值，得出γ= 0.02 时，RMSE=0.73826和MAE=0.53945最小.

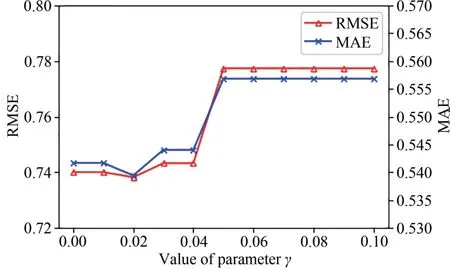
图3 γ值对误差的影响Fig. 3 Impact of parameter γ on error

在云服务器中，分别进行了多组实验确定参数对算法性能的影响，图4为确定参数k对F-SVD算法性能的影响，k为取最相似的用户数量，可见随着k取值的增大，RMSE 和MAE 误差曲线先降低，在k=18 时取最小值，随后误差稳步上升.当最相似的用户数过少，会出现一定的偶然性，容易造成误差较大.当取值较大，相似性较低的用户不能够很好地代表当前用户的偏好.当k= 18，此时误差最小，RMSE=0.75067，MAE=0.59075，即选最相似的前18个用户评分取均值代替传统的单源数据效果最佳.在目标函数里k位用户的评分均值占了预测评分很大的一部分，选择合适的k值对预测评分很重要.

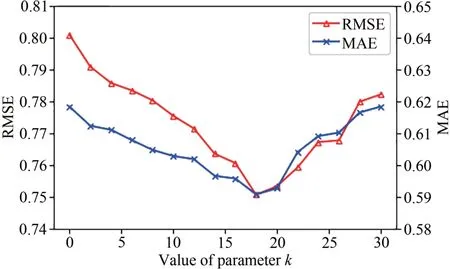
图4 k值对误差的影响Fig. 4 Impact of parameter k on error

图5 为验证参数α对F-SVD 算法性能的影响，表示用户在不同类型电影上的评分对预测评分的影响.随着α的增加，RMSE和MAE误差在0～0.72呈现降低的态势，在α= 0.72时误差最小，此时RMSE=0.78685，MAE=0.61597，随后呈现稳步上升的趋势.当α值较小时，用户在同种类型电影上的评分对总预测评分的影响过小，此时预测评分可能出现偏低的情况，从而导致预测误差增大.同理，当α值较大时也会导致预测评分误差增大.

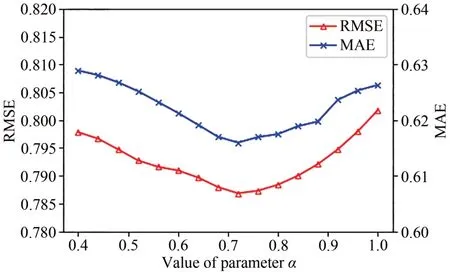
图5 α值对误差的影响Fig. 5 Impact of parameter α on error

图6 为参数β对F-SVD 算法性能的影响，表示用户对不同类型电影评分频率对预测评分的影响程度.随着β的增加，RMSE 和MAE 误差在0～0.56缓慢下降，当β= 0.56 误差最小，此时RMSE=0.79482，MAE=0.61134，随后出现稳步上升的趋势.当β取值过小时，用户在不同类型电影上的评分频率对预测评分的影响程度较低，此时可能导致预测评分偏小，从而导致预测误差增大.反之，若β取值偏大会导致预测评分偏大，同样也会使预测误差增大.

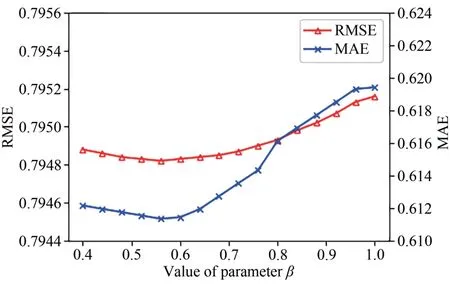
图6 β值对误差的影响Fig. 6 Impact of parameter β on error

综上，在多组实验对比下，各参数的取值分别为χ= 0.05，γ= 0.02，k= 18，α= 0.72，β= 0.56 时RMSE和MAE误差最小.

2.4 算法性能对比

在云服务器中将本文提出的F-SVD 算法在MovieLens-small数据集上与EnhancedCF［8］、RSVD［9］、Co-SVD［10］算法在RMSE、MAE、PRECISION 指标上进行性能对比实验.

在MovieLens-small 数据集下，从验证集中随机选择目标用户的近邻用户数，选取5～50 个近邻用户数，间隔为5，进行Top-10 预测推荐.图7～9 为EnhancedCF、RSVD、Co-SVD 和本文算法的RMSE、MAE、PRECISION对比图.

图7 不同算法的RMSE对比图Fig. 7 RMSE comparison diagram of different algorithms

根据图7 和图8，随着近邻用户数的增加，4 种算法的RMSE 和MAE 都逐渐下降，然后趋于平稳.近邻用户数较少的时候，基数较少，存在一定的偶然性，个别预测误差较大会导致整个结果的误差偏大.当用户数增加，基数增大，可以有效地降低个别预测对整个结果带来的误差.本文算法在近邻用户数为20 时趋于平稳，此时RMSE 为0.900，MAE 为0.674.可见本文算法在不同用户数情况下的误差都要优于其他算法，本文将计算用户相似度和多因素融合可以有效地降低预测误差.

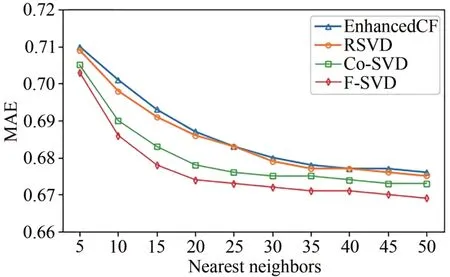
图8 不同算法的MAE实验对比图Fig. 8 MAE experiment comparison diagram of different algorithms

图9 为不同算法的预测精确度对比图.随着近邻用户数的增加，本文算法的精确度明显高于另外3个算法，当近邻数为20的时候，本文算法达到了最高的精确度，随着近邻用户数的增加，各种算法的精确度略微下滑.当近邻用户数较少的时候，基数较少，所以各种算法的精确度较接近.随着基数的增加，本文算法推荐的精确度优势逐渐体现.

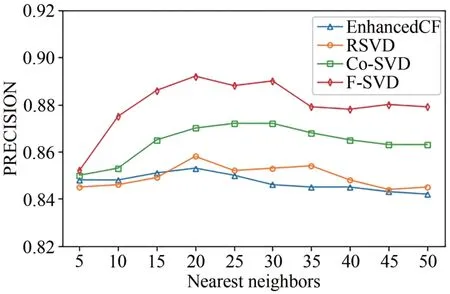
图9 不同算法的PRECISION对比图Fig. 9 PRECISION comparison diagram of different algorithms

图10 为不同算法在云服务器上的运行时间实验图.由图10可知：随着近邻用户数的增加，各算法的运行逐渐增加，本文算法运行时间要少于另外三种算法.由于在边缘服务器已经进行了用户相似度的计算和预测了用户对不同类型电影的预测评分，在云服务器中直接拿取结果进行计算，分担了云服务器的计算任务.

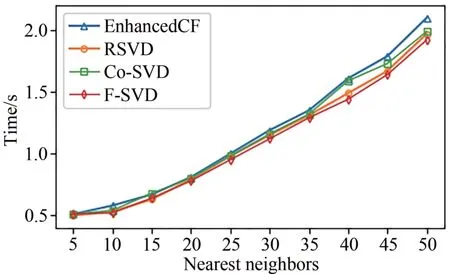
图10 不同算法的运行时间对比图Fig. 10 Execution time comparison diagram of different algorithms

图11 和图12 是加入BERT 后在MovieLenssmall 数据集上的RMSE 和MAE 分别随epochs 的变化趋势.实验结果表明：训练的前8 次，3 种模型的RMSE 值不断降低，到达最低点后，后面趋于平稳状态.本文算法在第8 次的时候RMSE 达到最低值为0.8793，MAE 最低为0.6590，Word2Vec 在第10 次的时候RMSE 达到最低值为0.8797，此时MAE 为0.6595，AutoEncoder 在第9 次的时候RMSE 达到最低值为0.8796，MAE 值为0.6593.因此本文算法具有较快的收敛速度，并且误差更小.

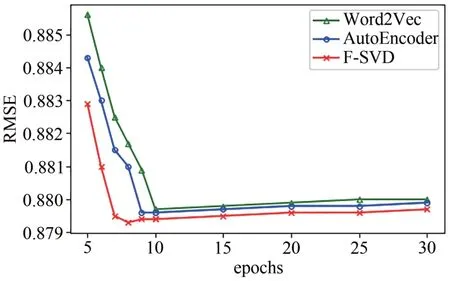
图11 BERT模型RMSE值的比较Fig. 11 Comparison of RMSE values of the BERT model

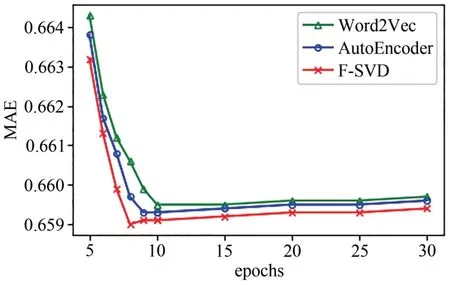
图12 BERT模型MAE值的比较Fig. 12 Comparison of MAE values of the BERT model

图13为加入BERT后在MovieLens-small数据集上的精确度随epochs 的变化趋势实验结果图，选择的近邻用户数为20，由图7 和图8 可知，当近邻用户为20的时候精确度最高.随着训练次数的增加预测的精确度逐渐提升，当达到最高值后，大体呈现略微下降的趋势，当训练次数为8的时候，本文提升的F-SVD 算法达到了最高的精确度，次数预测精确度为0.880，当训练次数为10 的时候Word2Vec 达到了最高的精确度为0.877，训练次数为9 的时候AutoEncoder达到了最高值为0.878.

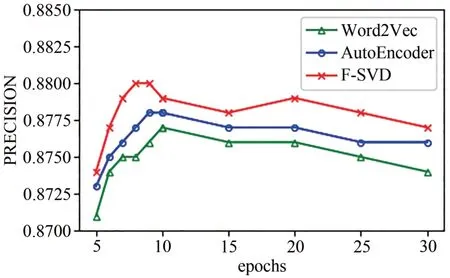
图13 BERT模型PRECISION值的比较Fig. 13 Comparison of PRECISION values of the BERT model

综上，本文所提的算法相比于其他算法，在MovieLens-small 数据集下，本文算法在RMSE、MAE上比其他算法总体上都要低，能有效地减小预测误差，表现最好.在预测精确度PRECISION 上，随着维度的增加本文算法要高于其他算法，故本文算法能够进行更精确地推荐.当加入BERT 模型训练历史数据，同样地具有更小的预测误差和更高的预测精确度.即本文算法能保持较低的预测误差，保证较好的预测精确度，还能够减少运行时间.

3 结语

本文以用户多属性和项目多属性为基础，提出了基于边缘计算的融合多因素的个性化推荐算法F-SVD，在数据稀疏、冷启动、数据复杂多样的情况下能降低评分预测误差和提高预测的精确度.在边缘服务器运用F-PEARSON 计算用户之间的相似度和运用BERT 模型对用户的历史数据进行训练得到用户对电影的评分，解决数据稀疏、冷启动下推荐效果不佳的问题.在云服务器运用F-SVD 挖掘用户、项目之间的潜在联系，以解决在复杂多样的数据下提取信息难的问题，运用随机梯度下降方法进行求解.实验结果表明：本文F-SVD 算法在不同评价指标上相比其他算法有较好的表现，表明本文算法能在保证较低的预测评分误差情况下同时具备不错的预测精确度.下一步将继续深入研究如何简化算法并提高算法的效率.