基于暂态数据戴维南等值参数辨识的时变广义短路比计算方法
2024-03-05孙锐鹏王奕鑫王玉昊吴浩辛焕海但扬清
孙锐鹏,王奕鑫,王玉昊,吴浩,辛焕海,但扬清
(1.浙江大学电气工程学院,浙江 杭州 310027;2.浙江省电力有限公司经济研究院,浙江 杭州 310008)
0 引 言
随着我国西北风电、光伏等新能源基地相继建成,各区域电网之间大规模、长距离输电形成多馈入直流系统[1]。多条直流馈入同一交流电网一方面消纳西北区域多余的风电光伏新能源电力,另一方面缓解了东南区域负荷需求大的现状,实现了电网的电力供需平衡,加快了电力系统向“高比例可再生能源”和“高比例电力电子设备”的新型电力系统转变的速度[2,3]。多条直流馈入同一交流电网加重了多条直流之间的相互耦合形势,产生交直流系统之间相互影响的问题,是影响电网安全稳定水平的因素之一。同时越多直流馈入同一交流电网,整个系统存在电压失稳风险,连续换相失败隐患,甚至导致系统无法安全稳定运行。
目前,单馈入和多馈入直流系统能否安全稳定运行一般由受端交流系统电网强度衡量。单馈入直流系统的受端交流电网强度由短路比表征,其定义为交流系统短路容量与直流额定容量之比。为了拓展到多馈入直流系统电网强度量化,国际大电网会议(International Council on Large Electric Systems,CIGRE)提出了多馈入短路比指标(multi infeed short circuit ratio,MISCR)、多馈入有效短路比(multi-infeed effective short circuit ratio,MIESCR)、多馈入相互作用影响因子指标(multi-infeed interaction factor,MIIF)[5]。虽然解决了描述受端交流电网强度评价指标缺失问题,但文献[6]指出MISCR、MIESCR与MIIF物理意义不明确,边界条件弱,并根据电压稳定分岔与系统雅可比矩阵奇异的等价性,建立交直流系统雅可比矩阵,定义了广义短路比指标(generalized short circuit ratio,gSCR),克服了传统短路比机理不明确的缺陷。
gSCR一般通过等值获得直流馈入节点的等值导纳矩阵计算。等值导纳矩阵的计算是电力系统阻抗辨识问题,基于电网的信息来源,该问题的解决方法一般分为两大类:基于网络参数与拓扑的白箱法和基于机电暂态仿真端口量测数据的黑箱法[7]。
第一类白箱法是基于已知完整的外网结构、线路元件参数和潮流信息,通过建立网络方程计算等值系统的戴维南等值参数。如文献[8]提出基于节点导纳矩阵的戴维南辨识方法,该方法基于全网信息,得到系统节点导纳矩阵,并对导纳矩阵进行修正、求逆求解戴维南等值参数,但该方法在电网状态改变时,无法准确求解[9-10]。文献[11]利用仿真分析了基于BPA-SCCP软件的多端口等值功能,阐明SCCP等值方法,但该方法不适用于系统参数时变的情况。
对于白箱法,其自身存在一定的局限性,一方面实际系统内部参数并非可以做到全知;另一方面系统的某些参数可能在不断的变化,而又难以精确描述。
第二类方法黑箱法是基于机电暂态仿真,获得等值端口机电仿真数据,提取机电仿真数据之中隐含的系统特征,经过数据处理等手段反推戴维南等值参数。最简单的黑箱法仅利用两个时间断面的仿真数据作差,可直接解出戴维南等值阻抗,故称两点法。此外,文献[12]提出一种基于时域仿真的戴维南等值参数辨识方法,其采用补偿法,结合全局网络方程计算等值节点处的开路电压和短路电流,辨识戴维南等值阻抗。但是该方法在形成全局网络方程时,将负荷统一看作恒阻抗负荷,忽略了系统非线性负荷的动态特性。
对于黑箱法,其在辨识数据上不可避免地会造成戴维南参数零点漂移问题[13];在方法上,不论是两点法还是时域仿真并补偿的方法,对于负荷都失去了有效性,原因是绝大多数负荷的阻抗模型是非线性的,节点负荷阻抗是变化的,其值与该时刻下负荷特性曲线的切线大小相关[14]。这表明将负荷统一为恒阻抗负荷无法计及非线性负荷对戴维南等值参数的影响。
为此,本文在机电暂态时间尺度下,提出基于戴维南多端口等值模型,采用最小二乘法辨识系统故障后暂态数据,得到受端交流电网的时变等值导纳矩阵,进而计算gSCR。通过单馈入直流仿真算例和某省级电网算例,本文分析了负荷对戴维南等值参数的影响,在减少了计算量的同时考虑了系统中各元件的动态过程,实现了对gSCR的进一步分析,精准量化了受端交流电网的强度,验证了所提方法的实用性和有效性。
1 基于戴维南等值的广义短路比计算
1.1 多馈入直流系统的戴维南等值模型
相较于单馈入直流系统,多馈入直流系统更为复杂,多条直流之间相互耦合同时直流系统与交流电网相互影响。因此,对多馈入直流系统在馈入节点做戴维南等值时,在尽可能简化其受端交流电网结构的同时突出直流间的耦合关系。多馈入戴维南等值结构将多馈入直流系统分为多馈入直流(multi-infeed direct current,MIDC)和受端交流电网。其中受端交流电网为研究区域,等值前多馈入直流系统如图1所示,等值后多馈入系统戴维南等值结构如图2所示。
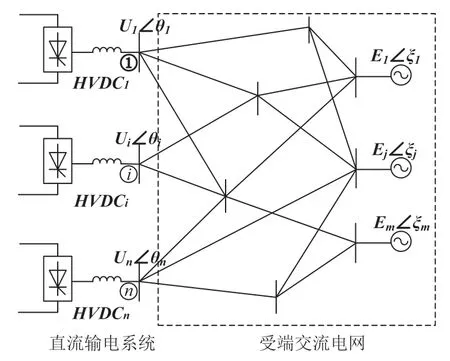
图1 多馈入直流系统
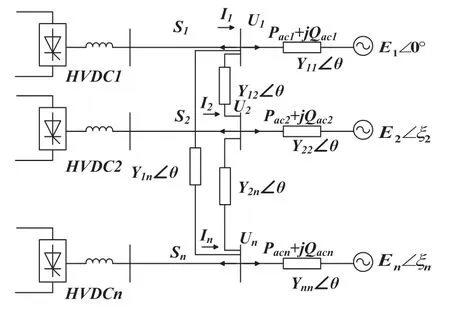
图2 多馈入系统戴维南等值结构
图2中研究区域等值端口数量n等于多馈入直流落点,Ui为端口等值节点的电压相量,Si为端口等值节点i注入研究区域的视在功率,其值等于研究区域内与端口等值节点i相连线路上传输功率之和。在研究区域每个端口节点i处,将研究区域等值为恒定电势Ei、Paci+JQaci、导纳Yii表示虚拟发电机的电压、功率和等值端口节点与系统各发电机之间的等值联络导纳。在研究区域端口等值节点i与端口等值节点j之间,将研究区域等值为导纳Yij=Gij+jBij,表示直流i和直流j的耦合关系。
1.2 广义短路比计算
文献[3]基于以下3个假设条件,提出多馈入系统广义短路比指标。
假设1:考虑的n条直流系统都是“相似的”,且控制方式都为整流侧定功率控制、逆变侧定熄弧角控制。即除了额定容量外,控制方式、以自身容量为基准的主电路参数标幺值都相同。
假设2:受端交流电网是电感型、拓扑连通的系统。
假设3:在额定点处直流系统注入交流系统的无功功率很小,即直流间直流落点间交流联络功率远小于其传输极限。
多馈入直流系统广义短路比定义为拓展导纳矩阵的最小特征值,即:
JB为研究区域的拓展导纳矩阵,具体为:
式中:Si为n馈入直流系统中第i条直流的额定容量。基于多馈入戴维南等值模型,可计算多馈入等值系统的节点阻抗矩阵,对节点阻抗矩阵求逆为多馈入等值系统的节点导纳矩阵,由式(2)可计算gSCR。特别指出,对于单馈入直流系统,其广义短路比为拓展导纳矩阵维数为一的情况[15],并基于式(2)可知,决定广义短路比的是系统等值阻抗。
gSCR描述多馈入交直流系统强度和稳定性时,须借助临界短路比(critical generalized short circuit ratio,CgSCR)辅助评判,特别指出一般CgSCR≈2,gSCR略大于2为弱交流系统,小于2为极弱交流系统[16,17]。特别指出,广义短路比计算基于拓展导纳矩阵的最小特征值,系统的导纳大小不能直接决定广义短路比的大小,但依据经验,导纳矩阵各元素越小,广义短路比越小。
2 基于暂态数据的时变戴维南等值参数辨识
2.1 基于暂态数据的多馈入时变戴维南等值参数辨识方法
戴维南定理表明:在任意时刻,交流电网可看作由等值电势通过等值阻抗进行供电的戴维南等值电路。当拓展到多端口时,n馈入交直流系统可看作n个等值电压源通过n(n+1)/2个等值阻抗进行供电的互联网络[18]。
如图2所示,t时刻注入研究区域端口节点多端口戴维南等值方程如下:
式中:上标t表示第t时刻数据,]T表示端口流入电流n维列向量,表示端口节点电压的n维列向量,Y表示多端口等值系统n×n的节点导纳矩阵,特别指出节点阻抗矩阵为Zth=Y-1,表示研究区域的等值电势,Y'为n×n的对角矩阵表示端口节点和等值电势之间的自导纳矩阵diag(y11,y22,K,ynn),其中对角元素分别表示等值节点的对地导纳。
根据式(3)在t时刻时,取式(3)的第i行,在端口节点i处有:
同时在仿真数据中,在端口节点i处注入:
根据式(4)和式(5),多馈入戴维南等值参数最小二乘估计模型为:
式中:m为在第t时刻的窗口大小,而端口节点个数为n时,可用的方程式共nk个。同时,式(3)中待求解等值参数Ei有n个,节点导纳矩阵Y是对称阵,有n(n+1)/2个参数,因此待求等值参数共n(n+3)/2个。随着多馈入直流系统中直流个数的增加,待求等值参数呈平方关系增加。若使得式(6)有解,则必须nm>n(n+3)/2成立,即m≥[(n+3)/2]。
将基于式(6)可辨识出在t时刻的戴维南等值导纳矩阵与结合n馈入直流系统中直流的额定容量,由式(2)计算出t时刻的广义短路比。
2.2 基于暂态数据的多馈入时变戴维南等值参数辨识计算步骤
多端口时变戴维南等值方法具体流程如图所示;
基于暂态数据多馈入戴维南等值参数计算方法的主要步骤如下所述:
1)对多馈入直流系统暂态仿真,选取故障恢复后等值端口的n个节点的电气量数据(S,U)。
2)计算端口节点的节点电压以及注入电流,并选取每时刻的窗口大小m。每时刻依据步骤1)的电气量数据,可得到n个端口节点的电压相量和n个端口节点的视在功率。计算在各个端口的电压电流,将后者除以该节点的电压并取共轭便得到流入n个端口节点处的电流相量,并由端口节点数n计算该时刻戴维南值参数的窗口大小m,将n×m个节点电压与注入节点电流数据作为步骤3)的辨识数据。
3)辨识该时刻的多端口戴维南等值参数。将步骤2)中计算n×m个端口节点电压和注入端口节点电流数据,建立如式(3)所示的方程,并基于此建立如式(6)所示的多端口戴维南等值参数的最小二乘模型,获得戴维南等值参数,形成受端交流电网的等值节点矩阵。
4)依据式(1)计算该时刻的广义短路比。
5)将窗口随时间移动,重复步骤1至步骤4,直到系统稳定结束,获得时变广义短路比。
3 电力系统负荷对戴维南等值参数的影响
3.1 戴维南等值参数理论值计算
系统等值阻抗可以根据网络阻抗以及负荷等值阻抗的串并联关系聚合得到,该聚合阻抗即为从等值端口看进去的理论戴维南等值阻抗。因此从外特性等价的角度来看,复杂系统总可以简化成图2中所示的戴维南等值模型[19]。
戴维南等值参数辨识的目标就是系统理论等值阻抗Zth,其可以作为验证辨识戴维南等值阻抗计算准确的依据。由于网络阻抗在暂态过程中保持恒定,后续需关注负荷等值阻抗对于戴维南等值参数阻抗Zth的影响。
从物理意义上讲,电力系统负荷是消耗功率,但不发出功率,因此在戴维南理论值计算中,将其按时变的等值阻抗。负荷节点i处的等值阻抗可结合t时刻与t−1时刻的负荷节点电压与注入电流求出:
3.2 静态负荷模型对于戴维南等值参数的影响
静态负荷由恒阻抗、恒电流和恒功率负荷组成,其中恒阻抗负荷为线性负荷;恒电流和恒功率负荷为非线性负荷模型。式(8)为静态负荷的数学模型:
式中:KPZ、KPI、KPP分别为有功负荷中,恒阻抗负荷、恒电流负荷、恒功率负荷所占的比例,且满足KPZ+KPI+KPP=1,KQZ、KQI、KQP类似。PL0为负荷有功分量初始值,QL0为负荷无功分量初始值,U0为节点电压幅值的初始值;PL为负荷有功分量实际值;QL为负荷无功分量实际值;U为负荷节点电压幅值的实际值。其计算值:
其中ux、uy表示负荷节点电压的实部和虚部。已知负荷节点电压U,可知负荷功率:
式中:ix、iy表示注入负荷节点电流的实部和虚部,可解得电流:
对式(11)线性化:
其中消去中间变量可得:
式中:Gxx为在该时刻线性化后电压实部对于电流实部的系数,类似的Bxy、−Bxy、Gyy为电压虚实部对于电流虚实部系数,其值如下:
引入如下转移矩阵:
利用上述转移矩阵T对式(13)进行变换,可得:
其中Ypn各个元素为:
故静态负荷线性化后的戴维南阻抗为:
将不同的KPZ、KPI、KPP,与KQZ、KQI、KQP带入式(18)。当且仅当KPZ=KQZ=1,即ZIP负荷为恒阻抗负荷时,负荷戴维南等值阻抗恒定不变,由式(18)可得其值为:
此外在ZIP负荷系数取其他值时,由于z12≠0,因此,非线性负荷的戴维南阻抗包含电流向量共轭的耦合项,与各时刻电压电流相关。如在电流变化较大的时刻,传统认为非线性负荷是恒阻抗的做法对于戴维南等值参数具有较大的误差。
4 算例仿真分析
4.1 单馈入构造算例
基于PSD-BPA暂态仿真软件搭建单馈入直流系统模型,以验证图3中提出的基于戴维南参数辨识的时变广义短路比计算方法的有效性,并分析负荷特性对时变广义短路比的影响。
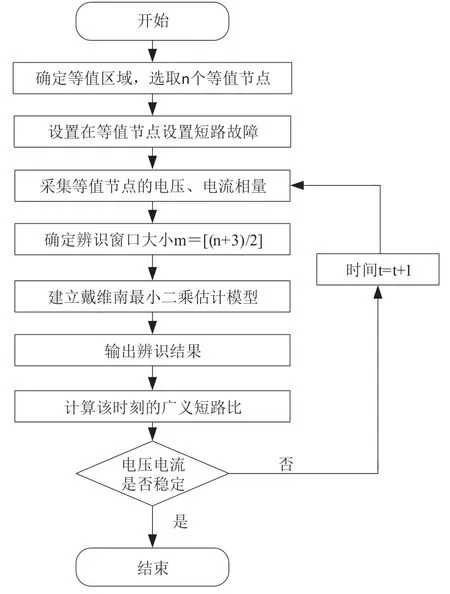
图3 多馈入直流系统戴维南参数辨识流程图
构造单馈入直流系统拓扑结构如图4所示,在节点1处对受端交流电网进行戴维南等值。电网中各参数如下:受端交流电网电压等级为500kV,基准功率为1000MVA,线路阻抗ZL1=ZL2=0.02+j0.06,负荷有功功率PL、无功功率QL分别为2000MW、1000MVar,其中静态负荷功率占比42%,感应电机占比58%,其中KPZ、KPI、KPP、KQZ、KQI、KQP系数分别0.13、0.34、0.53、0.13、0.34、0.53,E节点接入无穷大电源。在节点1处设置三相金属接地故障,故障持续 0.1s以故障切除作为辨识数据的起始时刻0时刻,每个窗口大小m为2,包含2个时刻的数据,窗口起始时刻至结束时刻时间间隔为0.01s,每个窗口计算出的广义短路比为窗口结束时刻的广义短路比。故障前系统戴维南理论阻抗为0.0489+j0.1170,广义短路比为2.4628,暂态数据中各节点电压与节点注入功率精度为10-5。
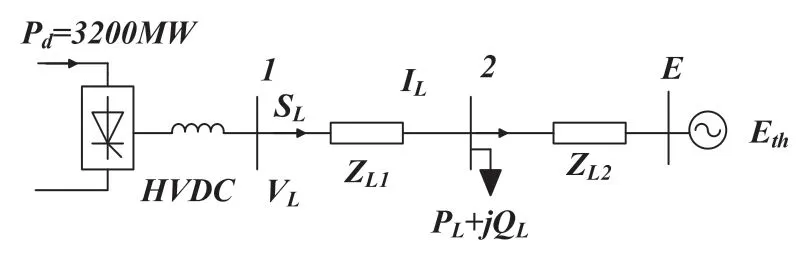
图4 单馈入直流系统等值算例
将综合负荷模型接入节点2,验证所提方法的准确性。节点1电压及注入功率如图5所示,故障清除后节点1的节点电压与注入功率在0.3s后基本保持不变。因此,选取节点1在故障清除后0~0.3s期间的U、S等电气量作为辨识数据,采用所提方法辨识系统等值阻抗,辨识与理论等值阻抗对比如图6所示,时变广义短路比对比如图7所示。
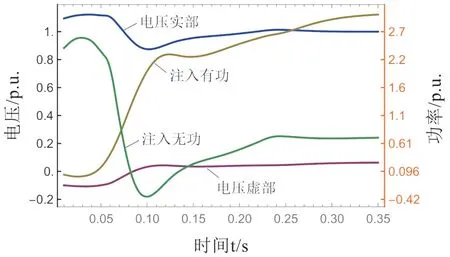
图5 节点1电压及注入功率

图6 辨识与理论等值阻抗对比

图7 时变广义短路比对比
由图5、图6和图7可知:
1)在图中,辨识与理论电阻、电抗以及广义短路比曲线基本重合,这是基于所提方法辨识得到时变电阻、电抗以及广义短路比,在0.3s范围内均能够较好拟合戴维南理论电阻、电抗和广义短路比;
2)在图中,广义短路比的变化趋势与等值电抗的变化趋势相反,这与单馈入直流算例中基于式(1)得出广义短路比与阻抗成反比关系结论相吻合;
3)在0.01~0.05s内,共有五个窗口,计算得到的每个窗口理论广义短路比从1.6541减小至0.5576后,迅速增大到7.4124,最后减小到2.9885。这是在期间内由于节点2处的感应电机负荷在故障恢复时,其有功功率从1543MW近似线性增加到1730MW,无功功率从1840MVar近似线性减小至1292MVar,同时负荷节点电压从0.9701增加到1.0325后,减小至1.0215。其中最大电压差出现在0.02~0.03s,为0.0216,使得由式(7)基于0.02s窗口内的电压、功率数据计算的负荷理论阻抗大,导致节点1处等值阻抗大,基于式(2)得到的理论广义短路比最小,为0.5576;同理整个期间0~0.04s功率线性变化,而0.03~0.04s的电压差最小仅为0.0011,使得在0.03s处得到的理论广义短路比最大,为7.4124;
4)当0.05s以后,系统理论阻抗变化不超过2%,其值与故障前戴维南理论阻抗0.0489+j*0.1170不超过变化2%,理论广义短路比变化不超过5%。由于感应电机暂态过程缓慢逐渐恢复至稳态,其中注入感应电机负荷的功率在1870MW、1220MVar附近,范围不超过3%,且负荷节点电压变化在0.1以内,负荷等值阻抗变化不超过2%,其值与故障等值前负荷阻抗接近,与恒定的线路阻抗聚合后,计算所得系统广义短路比接近故障前的广义短路比。
为了量化辨识戴维南阻抗、辨识广义短路比相对于理论值的误差,定义t时刻阻抗误差、和为:

图8 对比
为了进一步研究不同负荷对戴维南参数与时变广义短路比的影响,分别在单馈入直流系统节点2处接入恒阻抗、恒电流、恒功率、感应电机及综合负荷,计算五种负荷下系统的等值阻抗以及时变广义短路比,如图9所示,计算不同类型负荷的戴维南等值阻抗,如图10所示,分析不同负荷对单馈入直流系统广义短路比计算的影响。

图9 不同类型负荷的戴维南等值阻抗
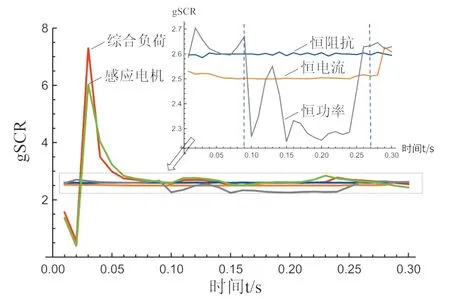
图10 五种负荷类型下的等值系统时变广义短路比
由图9、图10可知,节点2处连接不同负荷类型时,戴维南等值阻抗以及时变广义短路比是不同的,其中恒阻抗、恒电流、恒功率以及感应电机负荷对于戴维南等值阻抗以及广义短路比影响依次增大,这表明了忽略负荷的动态特性计算广义短路比是不准确的。
对于恒阻抗负荷,其暂态过程中负荷阻抗不变,由于算例中BPA数据精度问题,使得负荷等值阻抗变化略有波动,但不超过1%,因此理论广义短路比基本不变,故恒阻抗负荷特性对于广义短路比无影响。
对于恒电流负荷,相较于恒阻抗负荷,其计算的时变广义短路比总体更小。
1) 在0.01~0.27s期间,其时变广义短路比小于恒阻抗负荷的时变广义短路比。恒电流负荷在暂态过程中,电流基本不变,而电压从1.0214减小到0.8835,然后持续上升至0.9817,电压差最小在0.26~0.27s之间,为10-4数量级,使得在此期间由式(7)计算的恒电流负荷等值阻抗恒大于恒阻抗负荷等值阻抗,并与线路聚合得到的戴维南等值阻抗大于恒阻抗负荷戴维南等值阻抗,导致在恒电流负荷情况下的时变广义短路比小于恒阻抗情况下的时变广义短路比;
2) 在0.27~0.3s期间,其时变广义短路比增加0.1124,其值为2.6238。这是由于BPA输出精度为10-5,而在此期间节点2处节点电压差很小,实部与虚部范围分别为10-4数量级,注入恒电流负荷的电流差也很小,实虚部范围分别为10-5数量级,而该时刻广义短路比2.6238在考虑带入BPA误差计算得到时变广义短路比范围内,其范围为2.5089 ~2.8667。
对于恒功率负荷,其对于广义短路影响复杂,这是由于在为了满足负荷为2+j1,电压实部与虚部变化,导致电流实部虚部中的一个或两个向相反方向变化,使得基于式(7)的负荷阻抗呈负电阻或负电抗特性,需要结合电压电流变化分析负荷阻抗的变化,进而广义短路比变化复杂。
1) 在0.01~0.03s期间,广义短路比从2.5860增加到2.7042然后减小到2.6571,这是由于该期间负荷节点电压实部由1.0150上升至1.0179,而电压虚部由-0.1508减小到-0.1552,电流实部从1.7838减小到1.7736,电流虚部从-1.2498减小到-1.25334,计算得到负荷阻抗实部为负电阻,其中0.02s与其他时刻相比,其电流变化相较于电压更大,使得基于式(7)计算的负荷等值阻抗在该期间最小。
2) 在0.03~0.13s期间,广义短路比变化从2.6701减小到2.6653,随后增加到0.14s的2.5400,这是由于负荷节点电压快速恢复,实部虚部快速变化,其间电压实部增加了0.0136,电压虚部减少了0.0051,进而引起电流相反方向变化,其中电流实部减小了-0.0446,电流虚部增大了0.0173,此时由式(7)计算得到恒功率负荷阻抗与线路阻抗聚合后的系统等值阻抗最大,使得广义短路比在此阶段最小。
3) 在0.14 ~0.25s期间,广义短路比变化幅度较小,为7%,这是由于在每个窗口内,电流实部约线性增加0.0041,虚部约线性减小0.0210,对于电压实部线性增加0.0034,虚部线性增加0.0021,使得计算戴维南等值阻抗变化不超过10%;
4) 在0.26~0.30s期间,此时广义短路比相比0.25s最大增加0.3274,这是由于在0.09~0.25s前后负荷节点电压变化为10-4数量级,电流变化为10-3数量级,与恒电流负荷类似,由BPA输出精度造成此期间广义短路比计算范围应为2.2630~2.9662,该期间的广义短路比仍在此范围内。
对于感应电机负荷,在图中感应电机与综合负荷时变广义短路比两者变化趋势一致,但与综合负荷相比,感应电机负荷条件下的广义短路比最小值降低了0.1855,其最大值降低了1.282,这是由于单馈入直流广义短路比与戴维南等值阻抗成反比关系,而感应电机的戴维南等值阻抗变化比综合负荷大,其中戴维南等值最大阻抗约为综合负荷的1.5倍,最小戴维南等值阻抗约为综合负荷的1.2倍,导致广义短路比最值减小。这表明感应电机占比越大,时变戴维南等值阻抗最大值越大,计算所得时变短路比最小值越小。
4.2 实际系统算例
以某省级实际电网为例,验证本文方法的实用性。在实际四馈入直流系统中,设置四个馈入点同时发生三相金属接地短路故障,故障持续时间0.1s,四条直流线路的额定功率分别为8000MW,8000MW,8000MW,8000MW。记故障清除时刻为起始时刻,记录1s的U、S等电气量作为辨识数据。分别计算负荷为恒阻抗和综合负荷两种情况下的实际的馈入直流系统时变广义短路比,与SCCP等值计算的广义短路比相比较。其中SCCP等值方法基于网络参数与拓扑,将负荷按照恒阻抗处理求取戴维南等值参数,求取计算广义短路比。
图11为三种情况下实际电网的广义短路比,其中SCCP等值计算的广义短路比为2.0370。
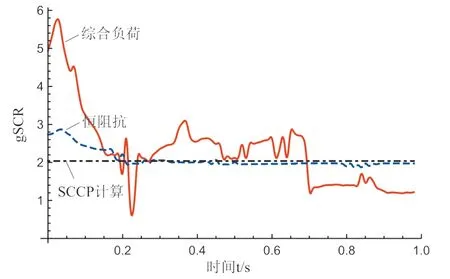
图11 三种计算条件下实际电网的广义短路比
由于实际系统中负荷采用综合负荷模型,为更好解释系统的广义短路比变化,将实际系统各直流端口节点注入有功功率绘制如图12。
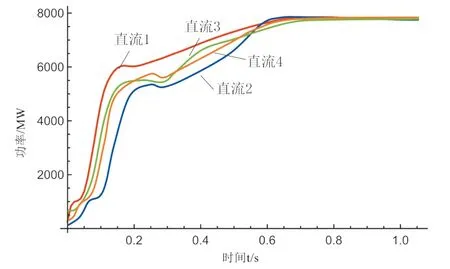
图12 实际系统各直流端口节点注入有功功率
由图11、图12可知:
1) 恒阻抗下与SCCP等值方法相比,恒阻抗情况下计算的广义短路比仍时变,且在0~0.2s广义短路比尚未稳定时大于SCCP计算值,而 0.2s以后广义短路比稳定小于SCCP计算值。一方面是由于系统中除了负荷以外,电力系统中其他元件具有动态特性,并增强了受端交流系统强度,使得0~0.2s的广义短路比大于SCCP计算值,并以同步机励磁系统为例,由于强励磁维持系统发电机节点电压,使得受端电网强度增强;另一方面,由于在系统稳定时,本方法将SCCP计算条件未考虑到的元件内部阻抗计算在戴维南等值参数中,使得戴维南等值阻抗整体偏大,导致在0.2s广义短路比变小;
2) 综合负荷与SCCP条件下广义短路比相比,更具有波动性,且两者相差较大,这表明在时变电力系统中SCCP计算误差较大,不能正确地反映时变系统的广义短路比,同时表明本文能够反映非线性负荷对于广义短路比的影响;
3) 综合负荷与恒阻抗计算条件下广义短路比,时变广义短路比相差最大为2.8912。这是由于在0 ~0.2s四条直流功率快速恢复,使得负荷节点电压快速增加,引起感应电机负荷暂态特性快速响应,导致感应电机负荷等值阻抗小,使得此期间系统广义短路比主要受感应电机负荷动态特性而变化。
5 结语
本文基于暂态数据,准确地辨识出多馈入系统戴维南等值参数,其中包含负荷特性、网络参数等电网信息,有效的避免将电力系统综合负荷按照恒阻抗方式处理的误差,同时反映了系统中广义短路比的变化,提出了一种计算时变广义短路比的方法。单馈入直流等值算例与实际四馈入等值系统结果表明,本文提示的方法具有较高的准确性,相比于SCCP等值方法本方法不仅考虑到不同负荷模型对于戴维南参数的影响,同时将其他元件的动态特性反映在内具有较好的实用性,在计算广义短路比更为准确,有助于准确量化受端交流系统电网强度。
