主成分分析法在水电机组运行监测分析中的适用性探索
2024-03-05金阳
金阳
(浙江省新能源投资集团股份有限公司,浙江 杭州 310020)
0 引 言
在电力市场化改革和生态流量等环保要求趋严等因素的影响下,部分水电站生产成本控制要求逐步提高。根据设备状态适当延长发电机组等主设备的计划检修周期,成为水电站降本增效的重要措施。因短期内以硬件冗余提高设备可靠性的空间有限,以软件解析冗余加强设备异常分析,即成为指导设备运行和开展检修的较优选项。
对于大多数水电站模拟量测点,包括温度、转速和压强等,计算机监控系统一般仅以输入值是否超过整定值作为判定条件将单个测点转化为布尔量,在与其他相关布尔量做逻辑运算后触发告警信号或停机等控制流程,而不进一步分析并表达不同测点之间的数值相关性。经过多年运行,一些水电站各类厂级信息系统已积累大量生产运行历史数据,为针对性开展测点相关性与设备状态分析奠定了一定的数据基础。
在针对设备状态分析的数学方法中,基于数据驱动的方法相较于基于解析模型和基于定性经验知识的方法,计算复杂度较低,更易于在实践中得到应用[1]。基于多变量统计的分析方法是基于数据驱动的方法的分支,能够在尽量避免根据基本原理建立复杂数学模型的前提下,提取对象的主要特征数据,以相对较少的信息维数反映系统主要信息。目前,基于多变量统计的分析方法在水电机组状态分析中的应用较少,主要原因是与化工等行业中许多以保持稳态为目标的生产运行过程相比,水电站主设备的运行受外部电网波动和内部环境变化等因素影响,过程难以保持相对单一的稳态。
本文采用基于多变量统计的分析方法中的主成分分析法,利用MATLAB对某水电站厂级信息系统中一台机组部分测点的运行历史数据进行离线分析,以此探讨主成分分析法在水电机组运行监测分析中的适用性。
1 主成分分析法
1.1 基本思路
主成分分析法是一种经典的基于多变量统计的分析方法,能够在将变量组偏差进行降维处理的同时,保留系统主要变化特征[2]。以主成分分析法为基础建立系统异常监测模型的主要思路,是以由正常观测偏差组成的训练集来确定变量之间的相关性,依此构建一组能够代表不同正交方向上系统最大正常偏差的向量组,并由其中变异性较大的若干向量组成新的空间。在设置适当的置信区间等参数的前提下,根据测试集中的观测偏差在新空间中的投影是否超限来判断系统有无异常。
1.2 建模与分析过程
(1)标准化观测值
选取有关测点组成变量组。因不同测点量纲不同,观测值可能存在数量级上的较大差异。为赋予每个测点变化量以等量权重,将各观测值减去平均值后除以标准差。平均值与标准差可由预先排除野值点后的初始训练集估定。
将初始训练集经过标准化后的数据矩阵记作
其中ynm表示第m个测点的第n个观测值的标准化结果。
(2)相关矩阵计算
测点相关矩阵为
因R为对称矩阵,可将其作特征分解为
其中Λ为对角矩阵,其对角元素为递减的正数特征值λ1≥λ2≥…≥λm≥0,V为相应的单位正交矩阵。在实际计算中亦可将Y作奇异值分解。
(3)确定主成分保留个数
为在保留系统主要变异信息的同时,一定程度上减少随机噪声对监测模型的干扰,需要统一权衡确定保留的主成分个数。方差累计贡献率法是实际中常用的一种方法。将Λ中的特征值按照从大到小排序,则相应计算式为
CPV即方差累计贡献率(cumulative percent variance)。当CPVl达到一定的较高百分比时,一般可以认为l个主成分已经可以充分表达系统状态变化[3]。该百分比可以根据有关监测需求及经验设置。
由V中的前l个向量组成m×l负荷矩阵P,并将原始测试集经过标准化后的数据矩阵记作Z,则表达Z在降维后的空间中的投影信息的得分矩阵T、系统返回重构估计值矩阵和系统残差矩阵E分别为
其中I为单位矩阵。通常情况下,与较大特征值对应的得分空间描述了系统的主要状态信息,与较小特征值对应的残差空间描述了随机噪声[4]。两个空间在方向上的变化可以同时分别监测。
(4)计算过程统计量
计算Z的各行向量z在得分空间中的T2统计量
和残差空间中的Q统计量
T2统计量即Hotelling'sT2统计量。Q统计量亦称SPE,意为平方预测误差(squared prediction error)。
(5)训练集野值点排除
当原始训练集采用大规模样本时,可以先对其自身标准化后的样本集合进行T2统计,并相对欠保守地确定阈值并排除野值点[5]:
或仍以单个测点观测值是否不在整定值上下限范围内作为判定观测值组是否为野值点的条件。两种方法容错率存在一定差异。本文采用第二种方法。
(6)异常检测
由训练集确定的T2统计量阈值为
其中α为给定的显著性水平,Fα(l,n−l)为自由度为l和n−l的F分布的上α临界点[6]。实际中,α的选择本质上是任意的,但又严重受限于习惯,通常取较小的数值[7]。
SPE阈值为
当T2≤Tl2或Q≤Qα时可判定系统正常,反之,则可判断系统存在异常因素。因T2统计量和SPE的阈值计算方法不同,二者对同一空间不同长度投影发生异常的敏感度不同,不能笼统比较优劣[9]。
(7)异常因素识别
贡献率图法是一种常用的用于识别导致T2统计量异常因素的方法[10],其主要步骤如下:
将满足式(13)的ti算作造成异常的得分:
其中z'为Z中已被判定为异常的行向量,pi为负荷矩阵P中第i个负荷向量,λi是相应的特征值,1≤i≤l。
z'的第j列元素z'j即测试集中第j个测点在相应时刻观测值的标准化结果,其对于异常得分ti的贡献率为
其中pj,i是pi的第j行元素。当计算结果为负数时,将贡献率conti,j计为0。
z'j对于该时刻所有异常得分的总贡献率为
根据总贡献率CONTj从高到低对各测点进行排序,溯源总贡献率较高的测点的原始观测值,结合经验推断系统在该时刻异常的具体原因。
尽管总贡献率CONTj对较小特征值的误差较为敏感,但在异常观测值组较少,利用方差分析实际可能不易识别残差空间中的异常因素的情况下,贡献率图法也可以应用于SPE的异常因素识别。
本文为简化判辨过程,将单个测点在不同时刻的总贡献率进行了累加分析。
2 水电机组运行监测分析
2.1 水电机组测点筛选
(1)对象机组简介
本文选取某水电站一台4MW发电机组作为监测分析对象。该机组采用自并励静止励磁系统,水轮机为混流卧式,出线经一台主变接入电网。其计算机监控系统采集的各传感器数据已实时上传至该水电站厂级信息系统。
(2)测点选取
主成分分析法以多变量统计为基础,在选取监测变量时,为避免将全范围内的大量甚至所有变量数据混杂地通过监测模型得出可能错误的结论,需要剔除与分析目标无关的变量,以及虽然和分析目标有关、但为冗余或者存在大量噪声的变量。同时,因在低维情况为正态而在高维情况为非正态的数据集通常是少见的[11],由此,可以通过拟合单个变量的观测值来判断其是否接近正态分布及是否宜纳入监测模型。
对于主要的电气量,虽然机组在一般正常情况下主要以额定功率等为目标长时间运行,但受一次调频、AGC、AVC及电网其他波动因素影响,其过程观测值实际仍然是非平稳动态的。机端相电压等测点观测值仅在特定的统计周期内近似正态分布,如果与其他非电气量共同作为监测变量,将对阈值确定等产生不利影响。对数、差分等变换往往难以直接改善最终分析结果,降低数据精度则将增加主观因素。
水电机组的主要非电气量包括温度、压强和转速等。正常情况下,轴瓦或其相应油槽等位置的温度测点精度相近,到达稳定值后的变化率差异较小。而机组空冷器的冷、热风等位置的温度测点更易受外部环境温度影响,不同时节差异相对较大。同时,多数油、水、气系统压强往往以一定区间而非恒值作为运行目标。水轮机转速与电气量中的机端频率均是机组最稳定的运行参数之一,两者信号源不同但高度相关,在特定条件下可只选其一。
本文主要选取非电气量作为监测变量,有功功率等电气量仅作为机组工况的外部判断条件。具体选取的变量测点顺序如表1所示。

表1 初始变量测点表
2.2 离线数据分析
在实际数据量较大、各测点采样频率不尽相同的情况下,本文统一将有关测点的采样周期设定为1分钟。对于采样时刻无数据的情况,以其前后观测值的平均值插入。统一设置分析过程涉及的参数,包括CPVl≥95%,α=0.01。由于机组开机运行后各温度测点到达稳定值的时间不同,为避免将较低温度误判为异常,采样起始时刻设定为机组有功功率到达额定值附近1小时后。
在MATLAB中建立监测模型,将水电站厂级信息系统中该机组数次以额定功率为目标,功率因数为0.96~0.98的运行过程历史数据以矩阵形式导入。
(1)机组A修前后的数据分析
以该机组A修前的一次运行数据构建训练集,A修后的一次运行数据构建测试集。具体可视化分析结果如图1―图4所示。根据训练集测算,前3个主成分的方差累计贡献率约95.14%。

图1 机组A修后T2统计量与A修前阈值的比较
在图1和图2中,测试集所有数据组的T2统计量和SPE均超过阈值,特别是在采样起始时间段。一方面表明机组在A修后相应的统计中心发生明显变化,另一方面表明尽管测试集采样起始时刻较晚,但仍有测点是在机组继续运行一段时间后才到达稳定值。
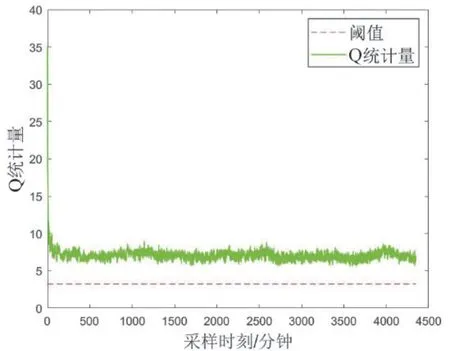
图2 机组A修后SPE与A修前阈值的比较
图3和图4显示,对异常的T2统计量和SPE的累计贡献率最大的分别是第4变量测点后导轴瓦温度和第3变量测点前导轴瓦温度。回溯原始观测值,发现后导轴瓦温度平均值经A修由约36.1℃降低至34.5℃,前导轴瓦温度则由约32.3℃降低至29.6℃,表明此次A修在降低有关部件运行温度方面取得一定效果。
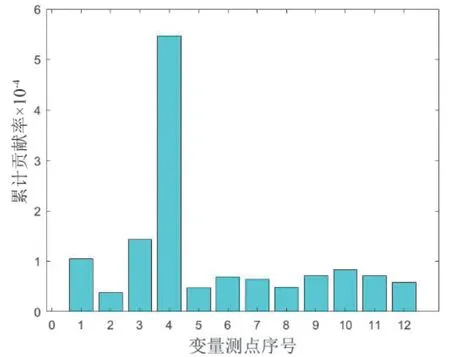
图3 测点对A修后异常T2统计量累计贡献率

图4 测点对A修后异常SPE累计贡献率
(2)机组同一可用周期内的数据分析
以该机组在此次A修后的一次正常运行数据构建训练集,经过一段备用时间后的一次运行数据构建测试集。在进一步延迟测试集的采样起始时刻后,可视化分析结果如图5―图8所示。根据训练集测算,前3个主成分的方差累计贡献率约95.71%。
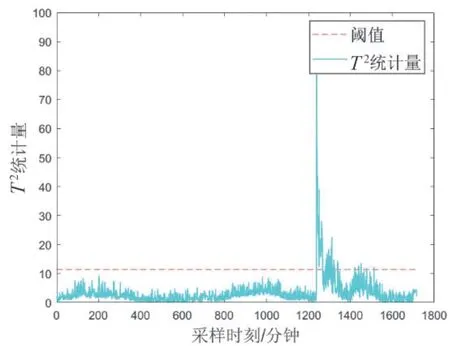
图5 同一周期内T2统计量与阈值比较
在图5和图6中,测试集数据组的T2统计量和SPE总体低于阈值,但在某一时刻突变以至远高于阈值。
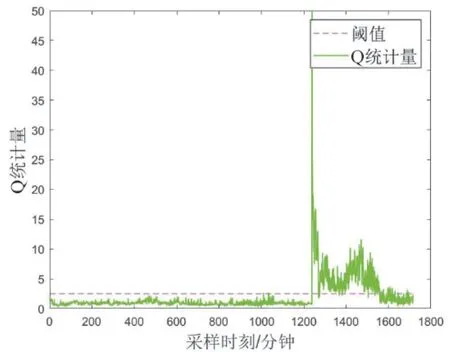
图6 同一周期内SPE与阈值比较
图7和图8显示第4变量测点后导轴瓦温度对异常的T2统计量和SPE的累计贡献率显著高于其他变量测点。回溯原始观测值,后导轴瓦温度在这一时刻由约34.5℃突降至31.7℃。导致测量结果存在粗大误差的可能原因,包括对应的PT100接线端子之间存在污染、变送器电信号受到干扰等。此时在计算机监控系统内,测点输入值未超过整定值,没有相应告警信号。

图7 同一周期内测点对异常T2统计量累计贡献率
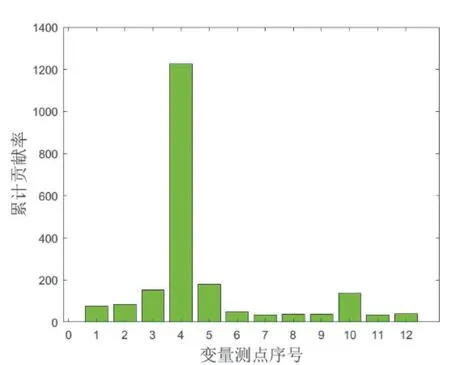
图8 同一周期内测点对异常SPE累计贡献率
3 结论
离线数据分析表明,在工况和测点分类的前提下,主成分分析法可以有限地应用于水电机组运行状态监测分析。尽管将观测值数据进行了压缩处理,但在基本保留测点之间的相关性的情况下,监测模型对于异常的敏感性一般高于单侧点的整定值。数据解析得出的异常结果往往是一种趋势变化的注意值,可以作为判断设备运行状态改善或恶化的参考条件。为使阈值尽可能控制在相对合理区间内,应在机组检修后重新设定训练集,同时需要剔除机组同一可用周期内较为早期的运行历史数据。
本文受限于该水电站各主要监视控制系统之间的通讯限制,未对水轮机导轴承的振动、摆度等测点开展分析。相较于温度,振动、摆度等测点能够更快到达稳定值且相对更少地受到环境因素影响。在具备有关条件后,可以在基本保留测点原始采样频率的情况下将其作为监测变量,同时将主成分分析法穿插于聚类分析等方法中以开展数据解析。
