数据驱动的燃煤电厂脱硫系统多目标优化
2024-03-05马永涛邢江宽罗坤樊建人
马永涛,邢江宽,罗坤,樊建人
(浙江大学 能源高效清洁利用全国重点实验室,浙江 杭州 310027)
0 引 言
我国煤炭资源较为丰富,煤炭消费占据重要地位。据国家统计局统计[1],2020年,火力发电用煤约占煤炭消费总量的52.3%,在源源不断地输送电力的同时,产生了如SO2、NOX、PM2.5等大气污染物。为控制大气污染物排放,我国政府出台了一系列的排放指标要求。湿法烟气脱硫系统能够有效脱除燃煤烟气中的SO2,因此,其被大部分燃煤电厂采用,作为主要的脱硫手段。在脱硫系统实际运行时,运行人员多根据自身经验调整优化系统运行参数,这样无法保证系统全时段实现经济稳定运行,因此,脱硫系统优化一直是研究者们关心的重要问题。
建立较为准确的湿法烟气脱硫系统(Wet Flue Gas Desulfurization,WFGD)排放预测模型是对其进行进一步优化的基础。第一性原理或机理模型,也被称为“白箱”模型,通过联立质量和能量守恒方程、运动学方程、热力学方程和输运方程等求解得到。这一类模型通常由有物理意义的相关参数来表征,并能在较大运行参数变化范围内保持其有效性,但是其结构较为复杂,建模的成本较高[2]。脱硫塔中的脱硫反应是复杂、多变量、强耦合、非线性的过程[3],难以建立其机理模型。近年来,随着计算机和人工智能技术蓬勃发展,使用过程数据来训练机器学习等人工智能算法的数据驱动模型或“黑箱模型”,因其建模成本低,被学者们用来建立多种复杂过程的模型。Chen等人[4]提出了一种宽深结构的长短时记忆神经网络模型,用来预测循环流化床的二氧化硫排放。Li等人[3]使用动态建模方法建立二氧化硫排放的预测模型,结果显示动态神经网络模型要优于其它模型。基于脱硫系统历史运行和实时运行数据,建立SO2排放预测模型之后,可以在较短时间内用较低的成本来优化脱硫系统的部分运行参数。Guo等人[5]基于组合数学模型和人工神经网络的SO2排放预测模型,使用粒子群算法优化湿法烟气脱硫系统。葛志辉等人[6]使用聚类算法挖掘得到脱硫系统可调运行参数的目标值,并建立了脱硫系统优化运行的目标库。但上述预测模型的建模准确性仍有待提升,并且大多为单目标优化研究,数据驱动的脱硫系统多目标优化需要进一步研究。
本文的研究目的是建立适用于湿法烟气脱硫系统的SO2排放预测模型,然后基于该模型对湿法烟气脱硫系统进行多目标优化。首先,本文基于某1000 MW燃煤电厂的运行数据,采用静态建模和动态建模两种建模策略,并对比建模效果;然后结合动态建模和一阶差分预测(Differential Prediction,DP)方法,对比随机森林(Random Forest,RF)、极致梯度提升(eXtreme Gradient Boosting,XGBoost)、支持向量回归(Support Vector Regression,SVR)、深度神经网络(Deep Neural Network,DNN)、长短时记忆(Long Short-Term Memory,LSTM )神经网络五种机器学习算法的建模效果,用决定系数(coefficient of determination,R2)和均方误差(Mean Squared Error, MSE)作为算法的评价标准。最后本文选取准确性较好的基于长短时记忆神经网络算法训练的模型作为SO2排放预测模型,使用多目标粒子群优化(Multi-objective particle swarm optimization,MOPSO)算法优化脱硫系统运行参数,将优化结果用来指导实际操作,实现脱硫系统稳定经济运行。
1 数据预处理和建模方法
1.1 异常值处理
在电厂机组实际运行时,由于设备故障等原因会产生明显偏离数据正常分布的值,即异常值[7]。如果将这些异常值作为训练数据的一部分,就会严重影响建模精度。如图1所示,烟气脱硫系统(Flue Gas Desulfurization,FGD)入口烟气SO2浓度数据中有一些异常值,因此有必要对原始数据进行预处理,剔除异常值。本文采用箱形图中使用的四分位距(Inter-Quartile Range,IQR)法来识别出原始数据中的异常值。找到任一维度数据的四分之一位数Q1,四分之三位数Q3,定义四分位间距QR为:
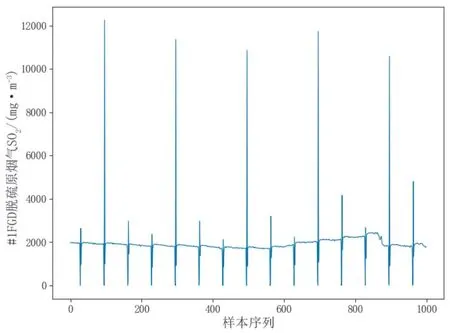
图1 部分样本的FGD入口烟气SO2浓度值
数据的上边缘Qup和下边缘Qlow分别定义为:
其中scale为尺度,通常取值为3或1.5,超过上边缘Qup或者低于下边缘Qlow的点被认为是数据中的异常点。当scale取3时,剔除的值为极端异常值;当scale取1.5时,剔除的值为温和异常值和极端异常值。
1.2 动态建模
本文采用动态建模方法[3],如图2所示,Xt(p×1)为当前采样时间维度为p的输入变量,Yt+1(l×1)为下一采样时间维度为l的输出变量。k为时间步,是一个超参数,可以根据实验和经验人工选取。若k值较小,可能无法包含足够的迟滞信息;若k值较大,就会导致输入变量的维度过大,从而延长训练时间。使用动态建模方法可以将输入变量重整如下:
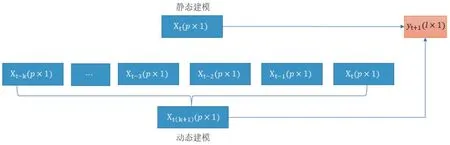
图2 静态建模和动态建模示意图
这样,输入变量就从p维扩展成了(k+1)×p维,总时间步为(k+1)。输出变量则保持不变,维度仍为l维。
1.3 一阶差分预测
一阶差分预测能减小预测数据的自相关性对预测结果的影响[4]。脱硫系统的数据具有明显的自相关性,因此一阶差分预测方法非常适用于对脱硫过程建模。本文结合动态建模和一阶差分预测,采用公式如下:
其中yt+1为t+1时刻预测目标变量值;yt则为t时刻预测目标变量值;Δy即为两个时刻预测目标变量的差值。本文所用模型通过预测Δy,再与yt相加,从而得到yt+1。
1.4 机器学习模型介绍
根据所使用算法不同,可以将机器学习模型分为集成学习、支持向量机和神经网络等。下面对本文所使用的算法原理进行介绍。
1.4.1 随机森林
由L. Breiman于2001年提出的随机森林算法已经成为一个极度成功的算法,被应用于各种一般性分类和回归问题上[8,9]。该算法是一种集成学习算法,通过训练多个不同的随机决策树,并对每棵树的预测结果取平均从而融合得到最终的预测结果。
1.4.2 极致梯度提升
极致梯度提升是由Chen和Guestrin于2016年提出的基于梯度提升且可扩展性较强的决策树集成算法[10,11]。由于其在多种机器学习任务中能有较好的表现和较高的准确性,它被广泛地应用在数据科学竞赛和实际生活中。该算法通过整合树模型和线性模型,最终做出预测,并使用正则化技术来防止过拟合。
1.4.3 支持向量回归
支持向量回归是一种有效的回归分析方法,其用数据集的子集来构建一个函数估计[12],数学形式如下:
其中W∈Rn,为权重特征矢量;b为偏置。代表估计出的映射关系;W∈Rn,为输入矢量。
支持向量回归使用核函数将输入数据映射到高维特征空间,将非线性问题转换为线性问题来求解。径向基函数(Radius Basis Function,RBF)是较为常用的核函数,它将输入数据投射到无限维特征空间,描述如下:
1.4.4 深度神经网络
深度神经网络是深度学习的基础。而模仿人类大脑行为的人工神经元则是构建深度神经网络的基础[13]。这个基础的计算元称为节点,它接收外部输入,通过学习获得内部权重和偏置参数,并利用这些参数产生输出。深度神经网络由输入层、隐藏层、输出层组成,每一层都由多个人工神经元组成,层与层之间通过权重连接。
1.4.5 长短时记忆神经网络
长短时记忆(以下简称LSTM)神经网络算法是一种善于处理非线性时序数据的神经网络算法[14]。与深度神经网络不同,LSTM网络层内也建立了连接。这就使得LSTM能反映出序列中的相关信息,模型有了记忆能力,其记忆用细胞状态表示。LSTM的记忆细胞由一个输入门、一个输出门和一个遗忘门组成[15]。这一结构使LSTM能够基于先前状态、当前记忆和当前输入,从而决定哪些细胞受到抑制、哪些细胞得到激活。
LSTM的结构如图3所示,其中xt表示当前输入;Ct-1表示上一时刻的细胞状态;ht-1表示上一时刻的隐状态;ft表示遗忘门的状态;it表示输入门的状态;Ct为候选细胞状态;ot表示输出门的状态;Ct表示当前细胞状态;ht-1表示当前隐状态;yt表示当前输出。σ(·)为sigmoid函数,作为门激活函数;tanh(·)是双曲正切函数,作为输入和输出模块的激活函数,数学描述如下所示:
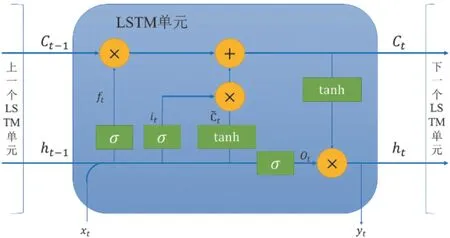
图3 LSTM的结构
1.5 多目标粒子群优化算法
粒子群优化算法是一个经典的群体智能算法,它被广泛应用于单目标优化问题的求解上[16]。由于其收敛速度快和实施简单,后来也被应用到多目标优化问题上。
第一个基于粒子群优化的多目标算法由Coello Coello等人提出[17]。在该算法中,帕累托(Pareto)支配被用来确定群体最优粒子和个体最优粒子,通过不断更新最优解集(Archive)将非支配粒子保存作为群体最优粒子。本文所使用的算法流程如图4所示:

图4 多目标粒子群优化算法的流程图
1.6 评价标准
对回归问题的评价标准主要有决定系数R2和均方误差MSE,具体计算方法如公式(10)和公式(11)所示:
其中n为样本总数;yi表示样本i目标变量的测量值;为样本i目标变量的预测值;为所有样本目标变量的测量值的平均。R2的取值范围为0~1,R2值越大,说明模型的预测能力越好;MSE越小,目标变量真实值和预测值之间的误差越小,模型的预测能力越好。
2 数据驱动的多目标优化模型建立
2.1 样本数据来源和建模问题描述
以某1000 MW燃煤发电机组的湿法烟气脱硫系统作为研究对象,收集到2022年10月至2022年11月间隔为54 s的系统相关运行数据,由文献[18]、[19]可知,该采样间隔是合适的,样本数量为50000,这些数据中可能存在异常值或者被记录下的非真实值,因此需要对其进行预处理,剔除异常值。
在获得数据后,选取合适的参数作为机器学习模型输入变量,将54 s后脱硫系统出口SO2浓度作为被预测量。随后基于该预测模型,对脱硫系统开展多目标优化。
2.2 模型输入参数的选择和异常值处理
本文在选取模型输入参数时,参考了相关文献[3,5]。需要说明的是,煤的工业分析和元素分析作为影响SO2排放的重要参数,但在采样数据所处的时间段内,煤质未发生显著变化,因此为简化模型,煤质信息未被选入输入参数。
为了衡量不同输入参数和被预测量之间的关系,本文首先计算异常值处理前各变量的皮尔逊相关系数rxy,计算方法如公式(12)所示,通常来说,rxy的绝对值越接近于1,两个变量之间存在线性相关的可能性越大。将得到的结果用热力图表示,如图5所示。随后用1.1中所描述的四分位距法剔除异常值,本文scale取1.5,再次计算各变量的皮尔逊相关系数,将得到的结果用热力图表示,如图6所示。最后使用处理后的70%的数据集去训练得到随机森林模型,运用模型特征重要度这一属性得出各输入参数的重要度,并记录在表1中。
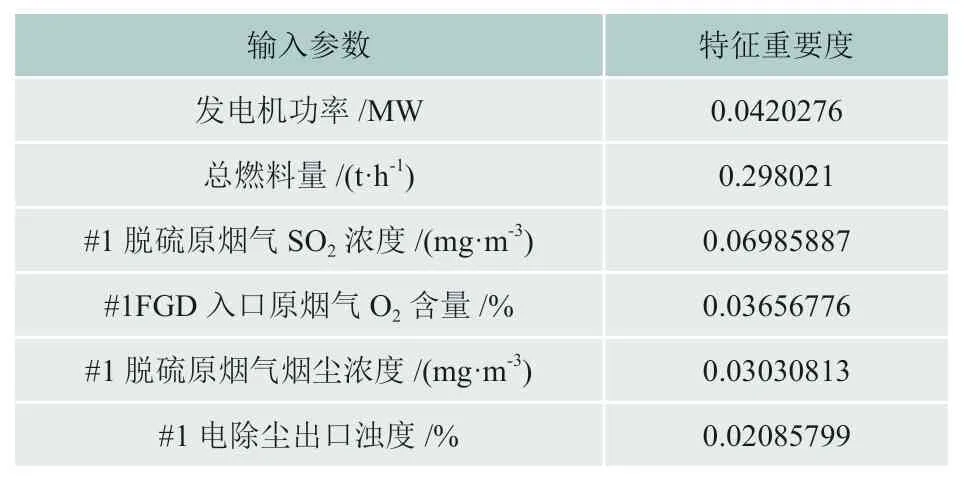
表1 不同输入参数对模型的输入重要性
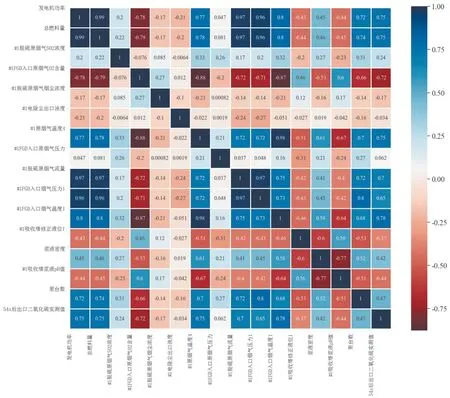
图5 数据预处理前模型输入输出变量彼此相关系数的热力图

图6 数据预处理后模型输入输出变量彼此相关系数的热力图
其中rxy表示样本x和样本y之间的皮尔逊相关系数;xi和yi分别代表样本x和样本y中的第i个样本;n为样本总数。
对比图5、图6可得,虽然数据预处理后#1脱硫原烟气SO2浓度和预测变量之间的rxy为-0.00019,但数据预处理前#1脱硫原烟气SO2浓度和预测变量之间的rxy为0.24,并考虑其特征重要度为0.06985887,因此保留这一参数。同时,从图6可以看出发电机功率、总燃料量、#1脱硫原烟气流量和#1FGD入口烟气压力1这四个输入参数存在一定程度的相关性,但为提高模型的预测能力,本文选择全部保留。最终选为模型输入参数的变量如表1所示。
2.3 动态建模总时间步确定
为确定动态建模时所需总时间步,本文使用随机森林和LSTM两种机器学习算法,对比在不同时间步下模型的预测效果。不同时间步下数据预处理后总量不同,每个时间步下70%的数据作为训练数据,30%的数据作为验证数据。其中使用LSTM建模时结合了一阶差分预测方法,而随机森林未使用。结果如表2和表3所示:

表2 不同总时间步下随机森林模型预测能力

表3 不同总时间步下LSTM模型预测能力
由表2和表3可得,不同总时间步下两种模型的预测能力稍有差别。对随机森林模型来说,总时间步为8小时,预测能力最好;对LSTM模型来说,总时间步为10小时,MSE最小,而总时间步为3小时,R2最大。这种情况是由总时间步不同和各总时间步下用于训练和验证的数据总量不同两种因素共同造成的。因此结合文献[3],同时为降低模型复杂度,本文将总时间步确定为5。
2.4 机器学习模型参数确定
为使机器学习模型获得较好的预测效果,通常需要对其参数进行调优,由2.3节可知,结合一阶差分预测时模型的预测效果较好,因此本文对结合了一阶差分预测的模型调整参数,同时总时间步设置为5小时,结果如下:
2.4.1 随机森林模型参数确定
影响随机森林模型预测效果主要参数为估计器数量,即nestimators,为确定其数值,采用五折交叉验证,用MSE作为衡量标准,根据结果本文将nestimators设置为200,模型其它参数为默认值。该参数下模型的建模效果如表4所示。
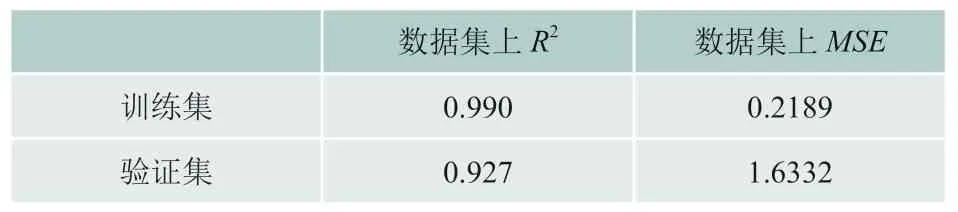
表4 随机森林模型的预测性能对比

表5 极致梯度提升模型的预测性能对比
2.4.2 极致梯度提升模型参数确定
影响极致梯度提升模型预测效果主要参数为估计器数量nestimators和学习率learningrate,为确定这两个参数的取值,分别采用五折交叉验证,用MSE作为衡量标准,根据结果本文将nestimators设置为100,learningrate设置为0.04,模型其它参数为默认值。当前参数下模型的建模效果如表五所示。
2.4.3 深度神经网络模型参数确定
影响深度神经网络模型预测效果主要参数为隐藏层神经元数量和隐藏层层数,为确定这两个参数的取值,基于Pytorch架构,70%的数据作为训练数据,30%的数据作为验证数据,并对数据进行标准化处理,参数batchsize设置为256,初始学习率为0.001,并逐渐减小,进行L2正则化,最终用MSE作为衡量标准,结果如表6所示:
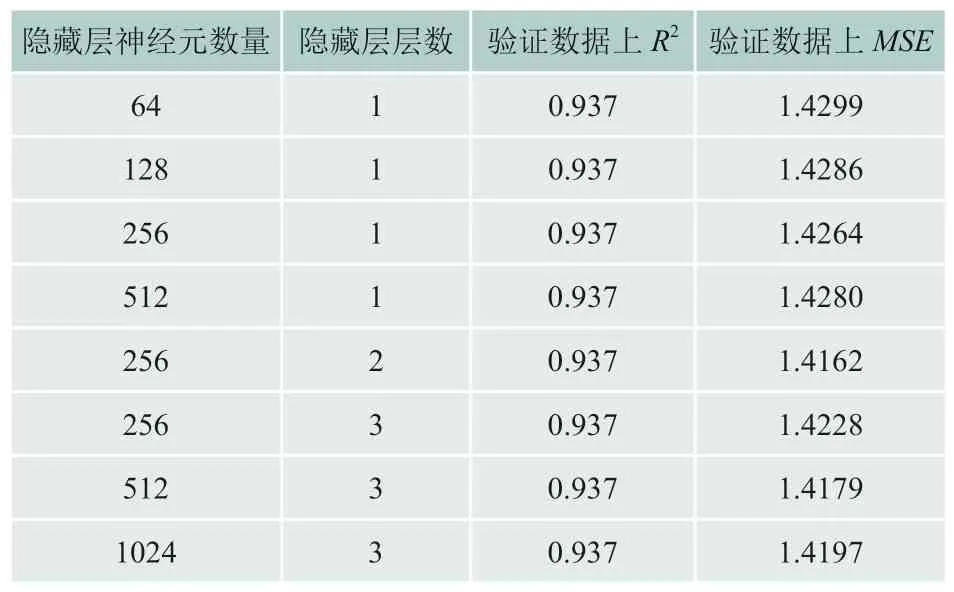
表6 不同隐藏层神经元数量和层数下DNN预测能力
结合表6数据,同时为降低模型复杂度,本文将隐藏层神经元数量设置为256,层数设置为2,其它参数为默认值。值得说明的是,除层数为1的模型外,为缓解过拟合,其它模型均使用了批标准化和丢弃,其中丢弃概率为0.1。
2.4.4 LSTM模型参数确定
影响LSTM模型预测效果的主要参数为隐藏层神经元数量和LSTM层层数,为确定这两个参数的取值,基于Pytorch架构,70%的数据作为训练数据,30%的数据作为验证数据,并对数据进行标准化处理,参数batchsize设置为256,初始学习率为0.001,并逐渐减小,进行L2正则化,最终用MSE作为衡量标准,结果如表7所示:
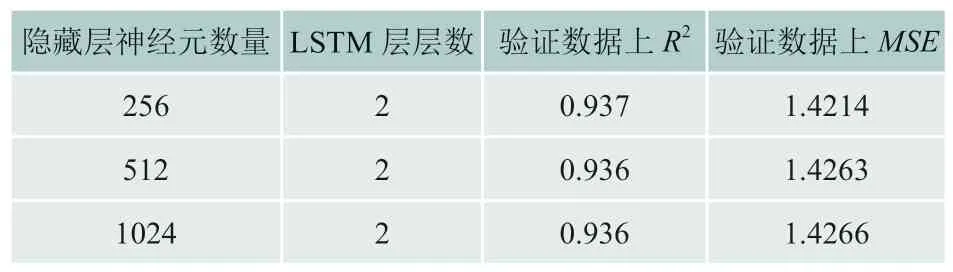
表7 不同隐藏层神经元数量和LSTM层层数下LSTM预测能力
结合表7数据,同时为降低模型复杂度,本文将隐藏层神经元数量设置为256,LSTM层数设置为2,模型其它参数为默认值。值得说明的是,为提升模型预测效果,在LSTM层后添加一层线性层,同时为缓解过拟合,使用了批标准化和丢弃,其中丢弃概率为0.1。
综上所述,本文确定了除支持向量回归外的四个模型的参数,在此处需要说明的是,对支持向量回归,本文选择默认参数。
2.5 多目标优化问题数学描述
由2.4节可知,针对五种模型,本文确定了相关参数,通过比较可以获得较好的SO2排放预测模型,随后可以基于该模型,并结合多目标粒子群优化算法,对脱硫系统相关参数进行优化。本文选择的待优化参数分别为#1FGD入口烟气温度1、#1吸收塔修正液位1、#1吸收塔浆液pH值、泵台数。本文所研究的问题为多目标优化问题,目标函数为SO2排放预测函数和脱硫成本函数,该问题数学描述如下:
其中f1(DV,MV)为前面训练好SO2排放预测函数;MV为操纵变量,即待优化参数,在给定范围内变化;DV为干扰变量,即其它输入参数;为脱硫效率;为脱硫塔出口SO2浓度;costWFGD为脱硫成本函数,即f2(DV,MV, ),以元/(kW·h)衡量,如公式(14)所示:
其中循环泵的运行成本Cpump和增压风机的运行成本Cfan分别用公式(15)、(16)计算:
其中Ui,Ii,φi分别为第i个循环泵的电压,电流和功率因子;Pelec是电价;load为发电机功率;Npump为浆液循环泵开启台数;G为烟气流量;ΔPtower为脱硫塔的压降;ηfan为增压风机的效率。
在消耗石灰石的同时,会生成石膏,其能带来一定的经济回报。从石膏得来的收益可以用公式(18)表示:
由文献[20]可知,离心式浆液循环泵始终在额定功率下运行,这样可简化循环泵运行成本的计算。
对多目标粒子群优化算法来说,本文将种群规模设置为100,代数为100,选择方法为轮盘赌方法。在一次次迭代中获得非劣解集,选取优化后参数值。
以上是数据驱动的脱硫系统多目标优化模型,下面第 3 节对该模型的效果进行比较分析和讨论。
3 结果和分析
3.1 静态建模和动态建模预测性能对比
为验证动态建模方法的有效性,本文使用SVR模型,对比其在静态建模(即总时间步为1)和动态建模(即总时间步为5)情况下各自数据集上的预测性能,结果如表8所示:

表8 支持向量回归在静态建模和动态建模下预测性能对比
由表8可知,动态建模情况下SVR模型的预测性能要优于静态建模,说明考虑了系统迟滞性的动态建模方法适用于对湿法烟气脱硫系统建模。
3.2 一阶差分和非一阶差分预测性能对比
为验证一阶差分预测方法的有效性,本文使用随机森林模型,对比其在结合一阶差分预测和未结合一阶差分预测情况下各自数据集上的预测性能,结果如表9、图7、图8所示:

表9 随机森林在结合一阶差分和未结合一阶差分下预测性能对比

图7 结合一阶差分预测下随机森林模型在验证集上预测性能
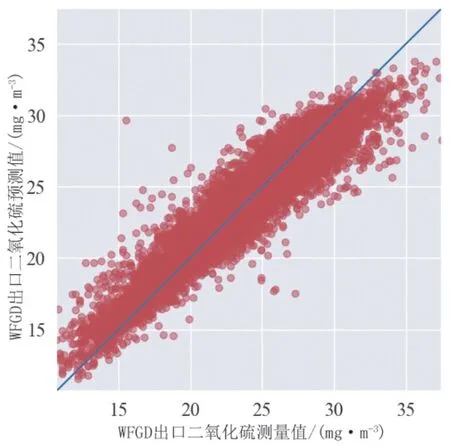
图8 未结合一阶差分预测下随机森林模型在验证集上的预测性能
结合表9、图7和图8可知,结合一阶差分预测情况下RF模型的预测性能要优于未结合一阶差分的情况,说明一阶差分预测方法减小了脱硫系统数据具有的自相关性对建模的影响。
3.3 五种机器学习模型预测性能对比
为确定预测性能最佳的机器学习模型,本文对比五种机器学习模型在结合动态建模和一阶差分预测方法情况下各自数据集上的预测性能,各模型参数设置参照2.4节,结果如表10所示。

表10 五种机器学习模型的预测性能对比
由表10可知,DNN和LSTM模型的预测性能要优于其它三种模型,说明这两种模型能较好地对湿法烟气脱硫系统中的非线性过程建模。考虑到LSTM模型更适用于时序数据,且LSTM模型在验证数据上MSE与训练数据上MSE之差小于DNN模型,因此本文选取LSTM模型为最优模型,其建模效果如图9、图10所示,相对误差在6%以内的数据占验证集总量的70%以上,值得说明的是,在验证集上,浓度在0~10 mg/m3之间的数据量仅为1,在其它浓度范围内相对误差小于5%的数据占比超过了50%。
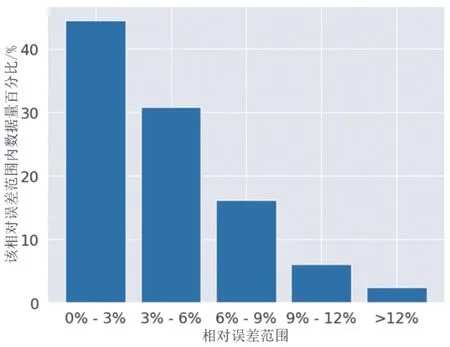
图9 LSTM在验证集上的不同相对误差范围数据百分比

图10 LSTM在验证集上的不同浓度范围内相对误差小于5%数据百分比
3.4 多目标优化结果
在获得最优SO2排放预测模型后,本文利用多目标粒子群优化算法,对湿法脱硫系统的部分运行参数进行优化,部分工况下优化结果表11所示。由表11可知,发电机功率较低时,脱硫成本一般较高。为降低脱硫成本,可尝试减小循环泵开启台数。为进一步说明各参数对湿法烟气脱硫系统的影响,本文分析了在发电机功率为380.442 MW情况下分别改变四个参数时WFGD出口SO2预测值和脱硫成本的变化情况,结果见图11―图14,竖虚线表示该参数的初始值。
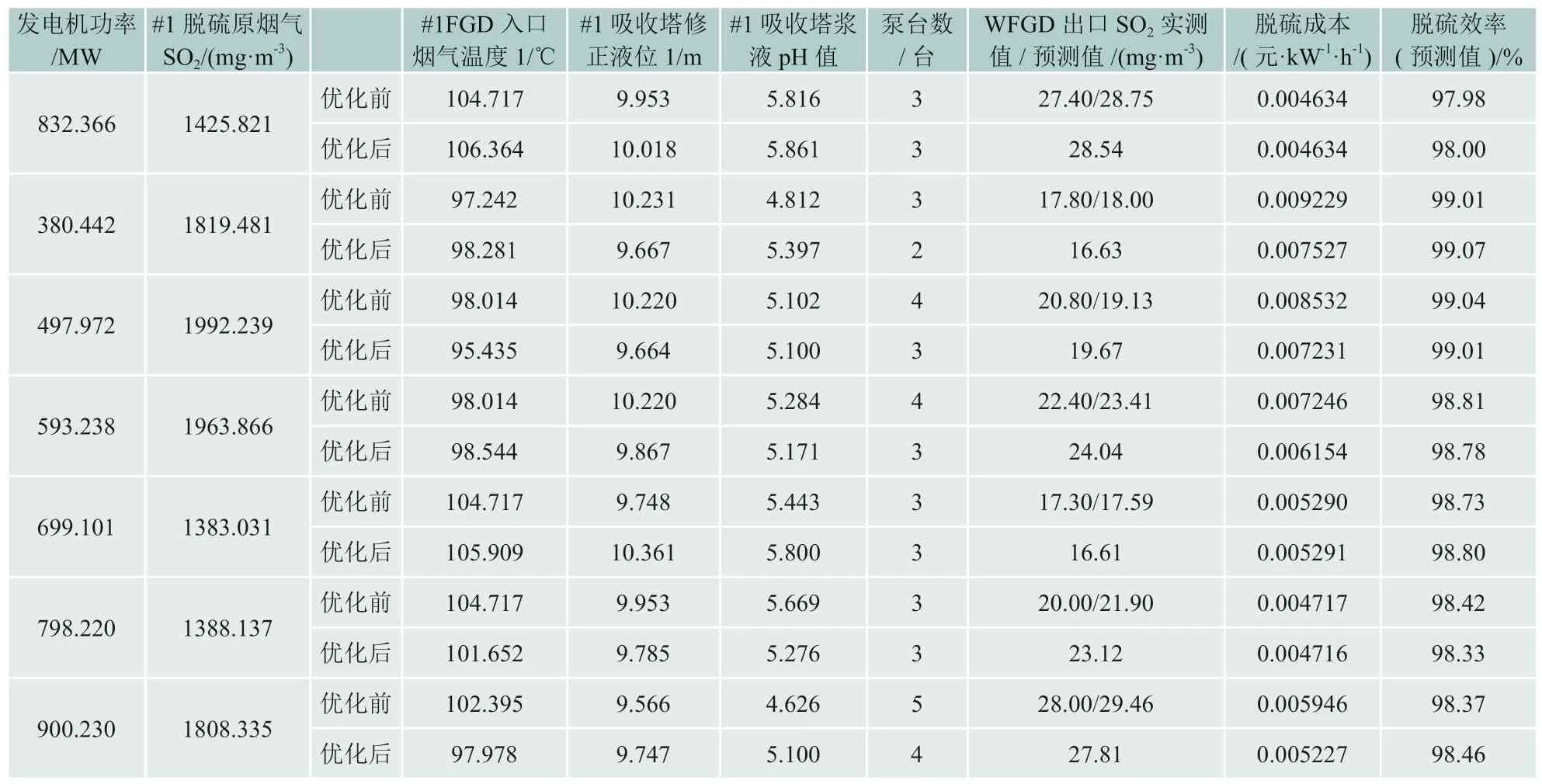
表11 部分工况下脱硫系统优化前后效果对比
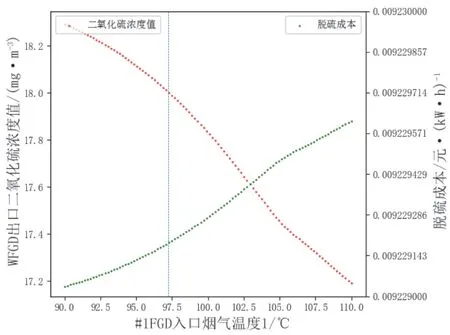
图11 WFGD出口SO2预测值和脱硫成本随#1FGD入口烟气温度1变化

图12 WFGD出口SO2预测值和脱硫成本随#1吸收塔修正液位1变化
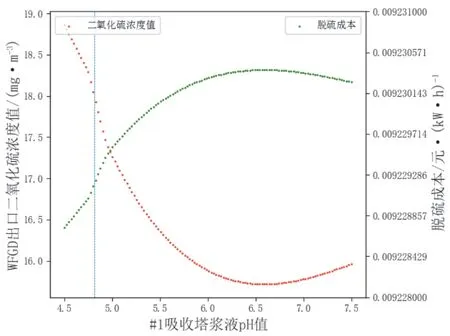
图13 WFGD出口SO2预测值和脱硫成本随#1吸收塔浆液pH值变化
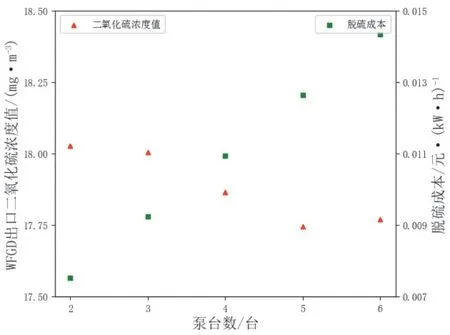
图14 WFGD出口SO2预测值和脱硫成本随泵台数变化
由图11―图14可知,在给定工况下,湿法烟气脱硫系统中#1吸收塔浆液pH值对脱硫过程影响较大,但并不是越大越好,实际运行时通常控制浆液pH值在一个合理范围内,一般认为选择在5.2~6.2为宜;从出口SO2浓度的视角看,另外三个参数的变化对其影响不大;但从脱硫成本的视角看,泵台数的变化对其影响较大,泵台数越多,脱硫成本越高,出口SO2浓度却没有明显下降,另外三个参数对脱硫成本则影响较小。权衡出口SO2浓度和脱硫成本,#1FGD入口烟气温度1的选择在98.281 ℃,#1吸收塔修正液位1选择在9.667 m,#1吸收塔浆液pH值选择为5.397,泵台数选为2台,此时脱硫成本下降了18.44%,出口SO2浓度则由于#1吸收塔浆液pH值的提升有一定程度的下降。
综上所述,本文提出的方法可以用来对湿法烟气脱硫系统开展优化。
4 结论
本文针对燃煤电厂湿法烟气脱硫系统脱硫过程建模存在的模型准确性不足的情况,采用数据驱动建模方法,通过箱形图对异常值进行识别删除,使用动态建模和一阶差分预测方法,用机器学习算法对湿法脱硫系统进行建模,对下一采样时间的脱硫系统出口二氧化硫浓度进行了预测,用决定系数和均方误差判断所建立模型的优劣,并对比不同机器学习算法的预测效果,选出效果较好的模型;并进一步基于数据驱动的脱硫过程模型,根据多目标粒子群优化算法,得到优化后的帕累托最优解集,在脱硫成本和出口SO2浓度之间权衡,在最优解集中选择优化的脱硫系统运行参数值。主要有以下几点结论:
1)由训练结果可以得出,动态建模加一阶差分预测的方法显著优于静态建模方法,说明动态建模加一阶差分预测的方法能较为准确地表征复杂的脱硫过程。
2)通过对比不同机器学习算法的结果,得出LSTM神经网络的建模能力略优于其它算法,说明LSTM神经网络能更好地处理时间序列数据。
3)根据多目标优化结果,随着脱硫成本的上升,出口SO2浓度逐渐下降;在实际运行时,运行人员可以根据优化结果,在脱硫成本和出口SO2浓度两者之间权衡,实现经济稳定运行。
