密林环境空地协同GNSS/UWB快速高精度定位技术

王星星,张子腾,3,盛传贞,蔚保国,张京奎,易卿武

(1.中国电子科技集团公司第五十四研究所,石家庄 050081;2.卫星导航系统与装备技术国家重点实验室,石家庄 050081;3.东南大学仪器科学与工程学院,南京 210096)

0 引言

现阶段,位置服务的获取主要依赖于全球卫星导航系统(global navigation satellite system, GNSS)。而在密林环境中,由于受地形和冠层的影响,卫星信号遮挡严重,观测值噪声大,多路径效应明显[1];此外,密林区域常常地处偏僻地区,通信受阻,使得卫星定位无法满足诸如森林资源管理、野外救援、森林巡护、边界与面积测量等应用的高精度定位需求[2]。

近年来,超宽带(ultra-wideband, UWB)作为一种新型的高精度无线交汇定位技术出现,利用极窄脉冲传输,具有强穿透性和抗多径能力,适用于开阔区、半遮蔽区、遮蔽区高精度定位[3-5]。目前,UWB定位技术已广泛应用于室内定位,但需提前在特定位置安装部署基站,对于临时定位场景来说使用不便且成本高昂。空旷环境下,无人机平台可快速运动,按需部署,由于其高度灵活,在应急环境下常作为空中基站与地面用户建立连接[6-8],利用无人机携带UWB布设可移动基站成为新的思路。有学者提出利用无人机携带GNSS/UWB移动基站辅助定位。文献[9]提出了一种融合GNSS/UWB的协同定位算法,在城市复杂环境下将UWB技术应用于车辆协同导航定位,精度达到分米级。文献[10]提出了一种UWB增强的车辆协同定位方法,通过现场实验生成真实数据集验证了方法的可靠性。文献[11]利用无人机搭载GNSS/UWB,配合地面界址点,按照单机绕飞、多点组网测距的方式完成界址点定位。可见,无人机结合GNSS/UWB的技术具有很多潜在价值,在密林环境下,综合考虑无人机平台在空旷环境快速运动与超宽带的强穿透性测量等特征,利用无人机搭载GNSS/UWB集成化载荷作为空中基站,理论上可实现林中标签高精度定位,为密林环境下高精度定位需求提供服务。

在此背景下,密林环境GNSS/UWB定位技术成为一项重要研究课题。本文提出了一种密林环境空地协同GNSS/UWB快速高精度定位技术,通过无人机携带GNSS/UWB集成化载荷,以移动单基站模拟多基站,配合密林中UWB标签组网测距,完成密林中UWB标签定位,针对运动载体,进一步提出位移辅助的定位方法。利用密林环境下实测测距实验+仿真定位实验对提出的方法进行验证,首先,在测试区域内对无人机基站布设方案展开研究;其次,通过实测实验分析密林环境下UWB测距误差;最后,设计仿真定位实验,统计定位精度。

1 定位模型

1.1 空地协同的系统构成与原理

目标进入密林后,由于卫星信号遮挡难以定位,利用搭载GNSS/UWB集成化载荷的无人机在密林上空空旷区域飞行,以移动单基站模拟多基站,建立可移动UWB测距网络,搜索密林中UWB标签信号,锁定UWB基站可布设区域,具体布设区域如图1(a)所示。图1(b)展示了空地协同定位原理,在密林上空,通过GNSS 星基增强实时动态精密单点定位(precise point positioning-real time kinematic, PPP-RTK)技术对基站位置实时标定,获取基站位置;在密林中,通过UWB测距系统进行测距,获取距离观测值。以基站位置和UWB测距量为原始观测值,基于空间后方交会原理构建观测方程,通过最小二乘算法[12]求解得到密林中UWB标签的绝对位置。

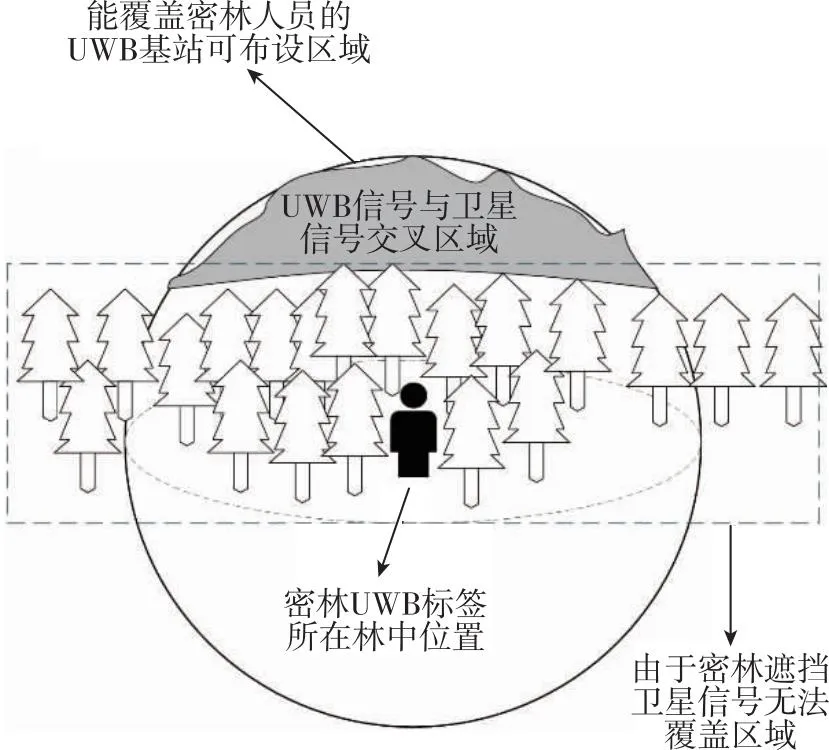
(a) 基站布设区域示意

1.2 定位模型

基于空地协同定位原理建立观测方程如下

(1)

式中,(Xn,Yn,Zn)表示无人机基站位置;Ln表示UWB测量距离;(xn,yn,zn)表示目标标签求解位置;n表示基站序号(根据无人机移动的时间先后顺序编号)。

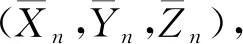
(2)

式中,(x,y,z)表示n=1对应时刻载体的初始位置,将式(2)代入式(1),位移辅助的动态定位观测方程如下

(3)

式中,无人机基站位置为通过PPP-RTK标定的坐标和载体位移建立的虚拟坐标。

为降低定位计算复杂度,使用最小二乘法求解待测点坐标,其函数模型为As=b,其中,A为系数矩阵,b为观测向量,s为未知参数向量,本文中对应载体位置(x,y,z)。对公式在s=s0|x=x0,|y=y0,z=z0处线性化,线性化之后观测方程表示为

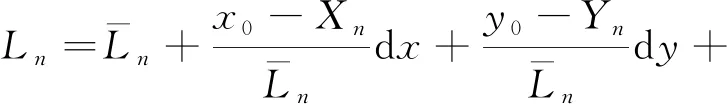
(4)

式中

则矩阵A和b表示为

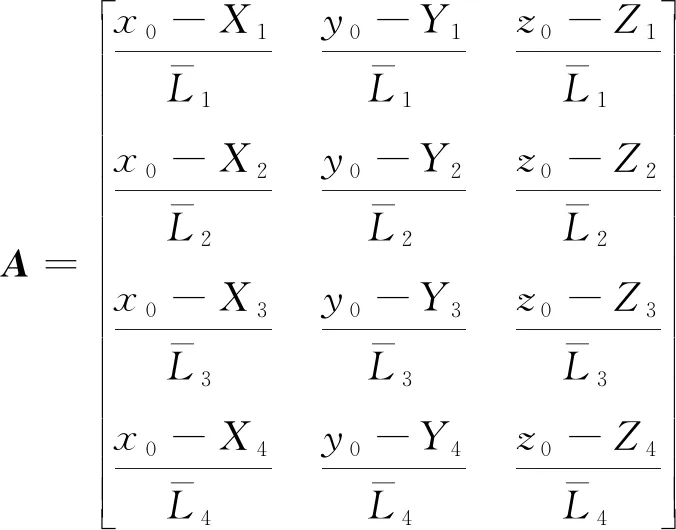
(5)

根据最小二乘原理求解待测点位置坐标并迭代求解,求解公式为s=(ATA)-1ATb。

1.3 精度评价

距离交汇技术的定位精度主要在于测距准确度、基站网型以及定位算法等参数[13],在定位算法确定的情况下,主要影响因素为测距准确度和基站布设。

在测距准确度确定的情况下,定位精度取决于无人机基站布设,可通过位置精度因子(position dilution of precision, PDOP)值衡量基站布设对定位精度的影响,以等高线图形式直观形象地表示出不同基站构型在测试区域内对不同点位定位精度影响的大小[14-15]。某点处PDOP值越小表示该处定位精度越高,在本文设计方法中,无人机基站布设的PDOP取值与基站布设的网型、范围(点位数量)及高度有关。

在无人机基站确定的情况下,定位精度直接取决于距离测量的精度,利用真实坐标计算真实距离,给定距离测量误差,仿真UWB距离观测值,然后按照空地协同定位方法计算目标位置,每点重复测量200次,并与真实坐标作差对比,计算均方根值(root mean square, RMS)评估其精度。

2 仿真实验

首先分析不同网型、不同范围、不同高度基站布设的PDOP值,然后根据实测实验确定UWB测距误差,最后设计仿真实验,分析定位误差。

2.1 无人机基站布设

(1)网型设计

本文使用无人机飞行模拟多基站,设计每隔1 s确定一个基站位置。考虑到无人机飞行速度恒定,相邻历元间基站距离相等,在同一高度面设计了4种网型,分别为正方形、折线形、菱形、直Z形,分析高度为100 m时的PDOP分布。选取200 m×200 m的实验区域,结果如图2所示。可以看出,正方形构型的PDOP值图像体现出良好的中心对称性,以基站为中心各个方向分布均匀,几何构型明显高于其他几种方式。因此,正方形构型不仅适用于初期标签位置未知时对目标的搜索,同时也适用于搜索到目标后对目标的测量标记。

(a) 正方形

(2)范围设计

设计无人机的巡航速度约为14 m/s,每1 s飞行一条边,可构成14 m×14 m的正方形基站网型,每点悬停1 s,7 s完成一次定位;每2 s飞行一条边,可构成28 m×28 m的正方形基站网型,每点悬停1 s,10 s完成一次定位;每3 s飞行一条边,可构成42 m×42 m的正方形基站网型,每点悬停1 s,13 s完成一次定位;每4 s飞行一条边,可构成56 m×56 m的正方形基站网型,每点悬停1 s,16 s完成一次定位。以80 m高度为例,不同边长的构型在200 m×200 m的区域内对应的PDOP如图3所示。

从图3可以看出,正方形边长越长,基站构型越好,表现在随着正方形边长的增加,相应区域内的PDOP值缩小,若边长成倍增加,PDOP值对应缩小。进一步地,组成42 m×42 m的构型需要13 s,这个时间可满足28 m×28 m构型在每边加密一点;同样地,组成56 m×56 m的构型需要16 s,这个时间可满足42 m×42 m构型在每边加密一点。如图4所示,可以看出,与42 m×42 m的4点正方形构型相比,28 m×28 m的7点正方形构型虽点位多,但是在测区范围内PDOP值更大;同样地,42 m×42 m 的 7点正方形构型PDOP值也比56 m×56 m 的4点正方形构型更大。也就是说,同样的组网时间下,增大网型范围对于PDOP值的优化效果优于加密网型基站点。

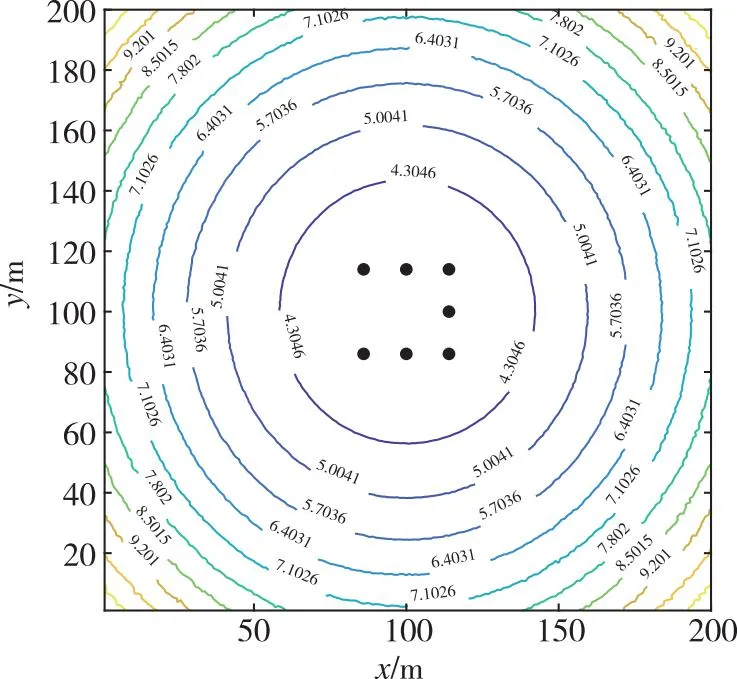
(a) 28 m×28 m

(3)高度设计

分析基站布设范围为14 m×14 m,28 m×28 m时,纵坐标为100,横坐标在0～200范围内,PDOP、水平分量精度因子(horizontal dilution of preci-sion, HDOP)、垂直分量精度因子(vertical dilution of precision, VDOP)随飞行高度的变化,结果如图5所示。可以看出,随飞行高度的增加,HDOP增加,VDOP减小,即受基站几何构型影响的平面定位精度随高程增加而减小,高程定位精度随高程增加而增大。而在三维方向上,PDOP值随着高度增加呈现先减小后增大的趋势,即三维定位精度随高度增加呈现先增大后减小的规律,且平面方向越远离基站,规律越明显。

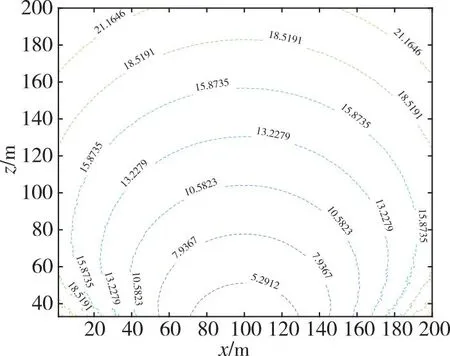
(a) 14 m×14 m基站构型PDOP

2.2 UWB测距误差分析

视距条件下,UWB测距误差约为0.1 m,而在密林中,由于树叶及枝干遮挡带来非视距误差。本节利用空循环LinkTrack P-B室内外高精度测距模组设计测距实验,分析其在树木遮挡环境下的测距性能。测试场景如图6所示, UWB基站布设于高楼窗边模拟无人机,标签在楼下广场移动,基站和标签之间始终有多层茂密大树遮挡。在每个标签点位均进行两组测距实验,一组直接利用LinkTrack P-B室内外高精度测距模组进行测距,另一组在同样位置放置GNSS天线,通过实时动态载波相位差分技术(real-time kinematic,RTK)解算高精度位置,然后反算求解距离。以RTK解算距离作为参考真值,分析UWB在树木遮挡环境下的测距误差。在整个实验过程中,标签放置于开阔或半开阔地带,可以接收到足够卫星进行RTK解算,保证了测距参考值的准确性。

图6 UWB测距误差测试场景

表1显示了RTK解算参考值,UWB测试均值、标准差(standard deviation, STD)及误差RMS,本次测试距离主要集中在100～200 m范围,从表中可以看出,在树木遮挡条件下,UWB距离STD分布于0.04～0.07 m之间,均值为0.05 m,误差RMS分布于0.05～0.29 m之间,均值为0.17 m。

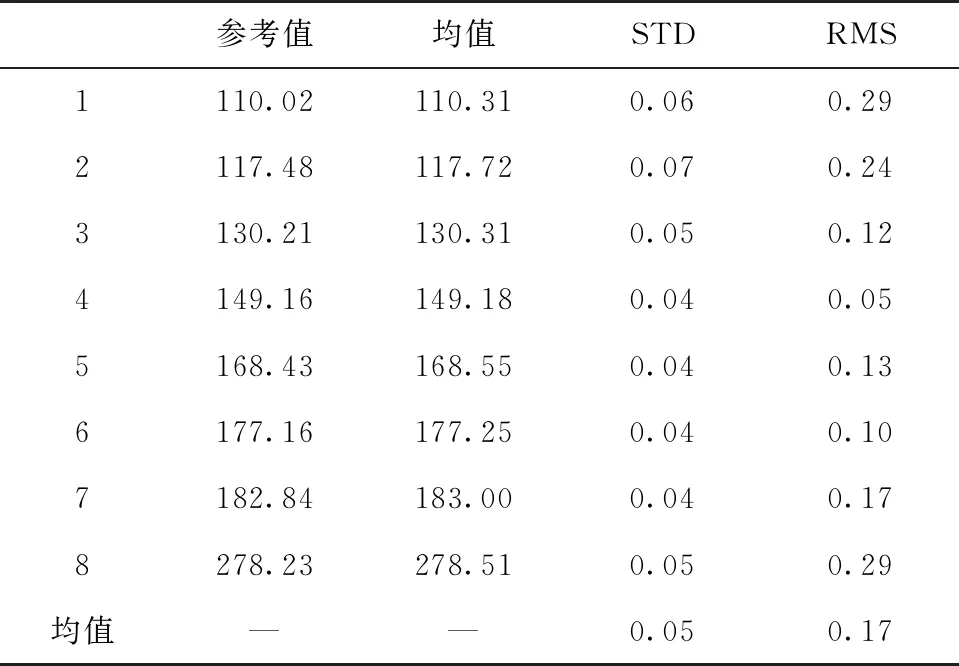
表1 UWB测距误差结果统计

2.3 仿真实验分析

通过无人机基站布设实验验证无人机基站布设对定位结果的影响规律,从UWB测距误差分析实验得出在树木遮挡环境下UWB的测距误差,将此两项分析结果应用于仿真测试中,开展3个仿真实验。实验1验证在静态条件下的定位精度,实验2验证在动态条件下的定位精度,实验3验证在测距误差变化条件下的定位精度。

(1)仿真实验1

本节仿真实验依据在密林下UWB测距误差结果,设计测距误差为0.2 m,方差为0.05 m,如图7所示。分析基站布设范围为14 m×14 m,28 m×28 m时,标签纵坐标为100,横坐标在0～200范围内定位误差随高度的变化,结果如图8所示。

(a) UWB测距仿真误差序列

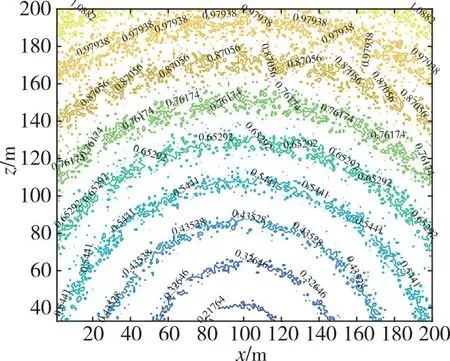
(a) 14 m×14 m基站构型平面定位误差

从图8可以看出,在同样高度下,28 m×28 m无人机构型定位精度优于14 m×14 m,也就是说,基站布设边长越长,定位精度越高,相应地,所需时间也越长,这和图3中PDOP值体现的规律一致。随着高度增加,平面定位误差增大,而高程定位误差减小,这和图5中PDOP值体现的规律一致。在高度80 m以下,测区范围内远离基站处三维定位误差随高度减小而增大;在高度80 m以上,测区范围内三维定位精度随高度增加而增大。综合来看,80 m是适用于整个测区范围内三维定位误差最小的高度。进一步观察在高度80 m处42 m×42 m基站构型在测区范围内的平面及高程定位精度,结果如图9所示。可以看出,在整个测区范围内,平面及高程定位误差均在0.3 m以内,基站覆盖区域内,平面及高程定位误差均在0.2 m以内。

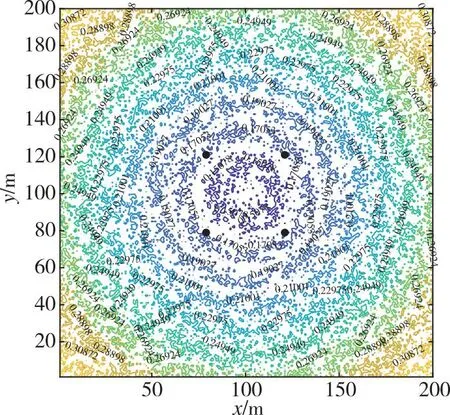
(a) 平面定位误差

(2)仿真实验2

仿真实验1实现静态载体的精密定位,根据式(3),要进一步实现动态载体的精密定位,需预先确定动态载体的位移。首先,进行运动载体的初始化,令载体在3个点位静止,完成静态定位,通过位置差分获取位移,之后开始运动,通过战术级惯性测量单元确定位移,每标定一个基站位置,对标签进行同步定位。具体位移情况如图10所示,载体在P4、P3、P2点位静止,完成静态定位,之后随机运动。为确定P1位置,需确定P1P2、P1P3、P1P4之间的位移,其中P1P2位移通过惯性测量单元确定,P2P3、P2P4位移由位置差分得到,和P1P2位移累加,即可得到P1P3、P1P4位移。一次动态定位后,本次定位的P4点不再参与下次定位,P3/P2/P1依次变为下次定位的P4/P3/P2,依次重复计算,实现动态定位。

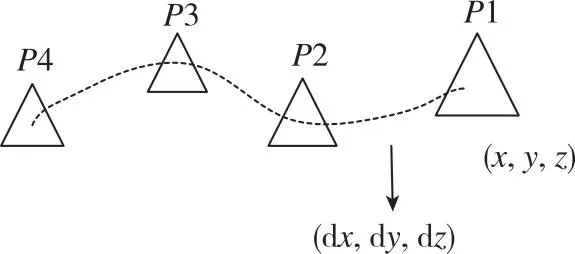
图10 运动载体位移图示

在测试区域内选择A/B/C/D4个点位,设计运动轨迹,根据轨迹变化仿真其位移,并在位移中加入方差为0.1 m的随机误差,利用式(3)求解在高度80 m处42 m×42 m基站构型在测区范围内A/B/C/D4点的平面及高程定位精度(测距误差设计同仿真实验1)。表2给出了在A/B/C/D4个点位标签静止与运动的定位误差对比,可以看出,运动载体的定位精度低于静止载体,整体保持在分米级。

表2 静止载体与运动载体的定位误差对比

(3)仿真实验3

在林中测距时,由于树干及树叶遮挡造成非视距误差,理论上,遮挡树木越多,非视距误差越大。对于林中标签点位而言,无人机基站飞行高度越高,信号传输在林中的距离越短,相应造成的非视距误差也越小。仿真实验设计为UWB信号在林中的传输路径每增大10 m,测距误差增大0.2 m。分析基站布设范围为42 m×42 m时,标签纵坐标为100,横坐标在0～200范围内距离误差、平面及高程定位误差随高度的变化,结果如图11所示。

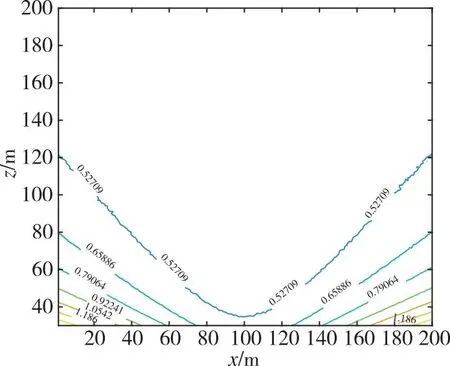
(a) 测距误差

可以看出,在测区范围内,随着高度增加,测距误差变小,在基站分布区域内,定位误差随高度增加而增加;在基站分布区域外,定位误差随高度增加而减小。在高度120 m以下,远离基站区域的定位误差大于0.7 m,综合来看,120～200 m是适用于整个测区范围内定位误差比较小的高度。以120 m为例,图12给出了42 m×42 m无人机构型在测区范围内的距离误差、平面及高程定位误差。可以看出,基站覆盖区域内,平面定位误差小于0.3 m,高程定位误差小于0.4 m,在整个测区范围内,平面定位误差为亚米级,高程定位误差为分米级。

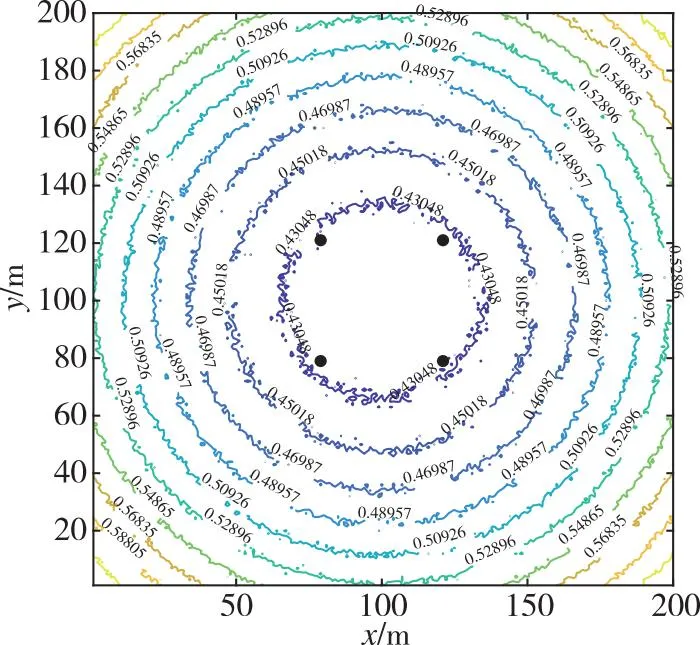
(a) 测距误差

3 结论

针对密林中卫星信号遮挡难以实现高精度定位的问题,提出了一种密林环境下空地协同的GNSS/UWB定位方法,为密林环境下快速高精度定位方法提供了理论支持。

1)利用无人机携带GNSS/UWB集成化载荷升空作为空中基站,并通过PPP-RTK技术对基站位置进行实时标定,大大节省了基站布设时间,解决了传统的 UWB可移动基站布设复杂、成本高等方面的问题。

2)对基站布设方案展开研究,验证基站布设对定位精度的影响。仿真结果表明,通过优选基站布设网型、范围及高度可有效提高定位精度,为密林环境下UWB定位技术的实际应用提供基站布设指导和依据。

3)对密林环境下UWB测距误差进行实测,并将统计误差应用于仿真实验。结果表明,选择合适的基站构型、范围及高度可有效实现密林环境下的快速高精度定位。

该方法仍有不足,主要不稳定因素在于UWB的测距误差,树林茂密且枝干粗壮区域,测距误差可能增大或者信号无法传播,需探索减少非视距误差及增强信号强度的方法,以增强定位算法的可靠性。本文基于仿真实验验证了空地协同GNSS/UWB定位算法的可行性。基于本文研究内容,我们正在研制GNSS/UWB一体化载荷,未来,将在大兴安岭密林地区对本文提出的定位方案进行实测验证。