基于反步法控制器的双缸液压系统同步运动控制研究
2024-03-05刘海星刘凯磊强红宾康绍鹏殷鹏龙
刘海星, 刘凯磊,,3, 强红宾,, 康绍鹏, 殷鹏龙
(1.江苏理工学院机械工程学院, 江苏常州 213001; 2.国机重工集团常林有限公司,江苏常州 213136; 3.江苏大学流体机械工程技术研究中心, 江苏镇江 212013)
0 前言
大型锻件在冶金机械、 电力设备、 兵器、 航空航天工业、 石油化工、 舰船制造、 重型车辆等装备中有着广泛应用[1]。 随着锻造液压机加工精度的提高,对锻造液压机双缸同步控制精度的要求也不断提高,目前, 已有许多学者开展了相关的研究工作[2-4]。 李胜永[5]设计了误差反馈的同步控制结构, 提高了同步控制精度。 李海军等[6]设计了灰色预测前馈控制器,该控制器能够控制双液压缸的同步误差保持在15 mm内。 张兵等人[7]针对强非线性和强耦合作用严重影响双缸同步系统控制精度的问题, 提出基于内力补偿和位置补偿的自由度控制策略, 通过仿真分析验证了该策略的有效性。 吴娜、 袁名伟[8]使用模糊-单神经元PID 控制算法, 通过仿真与实验验证了该算法的可行性。 薛召等人[9]针对传统PID 控制器同步控制稳定性不高的问题, 提出一种基于模糊单神经元PID 复合算法的双缸耦合同步控制策略, 通过仿真与实验证明该控制策略的合理性。 刘爱玲等[10]针对双液压缸同步控制的问题, 基于模糊控制理论提出了模糊前馈控制器。
然而, 锻造液压机液压系统存在活塞摩擦、 液控元件等因素会造成液压损失[6]; 再者, 锻件位置、 形状、 大小、 温度等因素会导致两液压缸受力不一致[11], 这些内在和外在因素会导致双缸同步控制精度降低, 不能满足锻造液压机工况的需求。
因此, 针对锻造液压机双缸同步控制精度不足的问题, 本文作者以传统双缸同步控制系统为研究对象, 建立液压缸位置控制系统运动学模型, 结合Lya⁃punov 稳定性理论, 设计基于模型的反步法控制器,并将该控制器应用到并联型同步控制结构中, 同时采用AMESim 和Simulink 构建双缸同步控制仿真模型,并将反步法控制器与PID 控制器进行仿真比较分析,为后续试验研究提供理论依据。
1 双缸同步控制系统组成
传统的锻造液压机双缸同步系统是由油源、 两个三位四通比例阀、 两个液压缸、 活动横梁组成。 文中对传统的大型液压机双缸同步系统进行改动, 在液压缸1 与液压缸2 左端右端各增加压力传感器, 在液压缸1 与液压缸2 活塞杆处各增加速度传感器、 力传感器、 位移传感器, 如图1 所示。
根据图1 对控制过程进行简要说明: 首先油源对该系统提供压力, 在对液压缸1 和2 提供指定位移信号后, 控制器将收集到位移传感器1 和2 的位移信号、 速度传感器1 与2 的速度信号、 力传感器1 与2的力信号、 无杆腔压力传感器1 与2 的压力信号、 有杆腔压力传感器1 与2 的压力信号, 随后控制器会控制三位四通比例换向阀1 和2 动作, 对液压缸1 和2进行油液补充和减少, 从而调整液压缸1 和2 活塞杆位移, 实现同步控制[5]。 控制的关键在于控制信号与传感器信号之间建立一种闭环反馈机制, 能够实现实时的液压系统变量调控, 以保障同步运行的精确度[12]。
2 位置控制系统运动学模型建立
液压缸位置控制系统运动学模型建立以液压缸1为例, 对其简化如图2 所示。 图中:ps为三位四通比例阀进口压力;pr为系统回油压力(一般设为0);p1为液压缸无杆腔压力;p2为液压缸有杆腔压力;Q1、Q2分别为流入和流出三位四通换向阀的流量;FL是液压缸承受的外负载力。
对该系统做以下假设:
(1) 假设ps是恒压源, 以ps的压力为系统供油;
(2) 系统中采用的比例方向阀为理想对称滑阀且具有零遮盖窗口;
(3) 比例方向阀的节流面积和节流阀口大小呈线性关系。
结合文献[13]的研究可建立电液伺服系统运动学模型为
式中:m为系统负载质量, kg;x1为液压缸输出位移, m;x2为液压缸输出速度, m/s;A1为液压缸无杆腔工作面积, m2;A2为液压缸有杆腔工作面积,m2;V01为液压缸无杆腔初始容积, m3;V02为液压缸有杆腔初始容积, m3;Ct为执行器泄漏系数;βe为液压油弹性模量;G为系统负载重力, N。
根据文献[13]可知比例阀动态方程可近似为
式中:τv、ki、u分别为比例阀时间常数、 阀芯电流增益及控制输入。 为了减小推导的复杂性, 简化比例阀动态环节, 即
为了使伸出或者缩回工况的流量方程合并成为一个方程, 定义变量s, 根据式(4) 可以通过输入值的正负对变量s的值做出调整, 即:
结合式(3) (4), 根据文献[13]可以列出流量方程如下所示:
式中:xv为阀芯位移;kq为流量系数, 展开为
式中:Cd为比例阀节流孔流量系数;w1、w2分别为比例阀阀芯节流孔左右两端面积梯度;ρ为液压油密度。 由于该三位四通比例阀是对称滑阀,kq1=kq2=kq, 同时也是一个定值。
令

先将式(10) 进行求导, 将式 (11) — (14)代入式(1) 中可以简化运动学模型为
从推导过程可以看出, 液压缸位移受到该运动学模型参数的影响, 从式(15) 中可以发现输入u控制x3的变化,x3控制x2的变化,x2控制x1的变化, 于是可以将式(15) 看成是从u至x1的3 个积分组成的串联积分系统。 所以作者从式 (15) 入手, 结合Lyapunov 稳定性理论, 研究基于模型的反步法控制器。
3 反步法控制器的建立
反步设计法是交叉选择Lyapunov 函数与反馈控制的递归过程, 是将整个系统的设计问题分解为一系列低阶子系统的设计方法[14]。
首先定义:
其中:x1d是指定位移;x2d与x3d是虚拟控制量。
第一步, 为了使误差e1趋近于0, 定义一个半正定Lyapunov 函数为

第二步, 为了使得e2趋近于0, 需要找到一个Lyapunov 函数包括e1和e2, 只有这2 个参数全部趋近于0, 系统才稳定。 定义半正定Lyapunov 函数:

第三步, 为了使得e3趋近于0, 需要找到一个Lyapunov 函数包括e1、e2和e3, 只有这3 个参数全部趋近于0, 系统才稳定。 定义半正定Lyapunov 函数:

从式(21) (28) (35) 可以看出控制输入量u由模型参数、 指令变量以及参数k1、k2、k3决定, 控制输入量u能够根据模型参数的变化实时调整, 可以通过调整参数k1、k2、k3对活塞杆位移属性进行控制。
4 双缸同步控制系统策略制定
目前, 串联型与并联型同步控制结构在同步控制中较为常用[5], 考虑到文中控制算法的独立性, 采用并联型双缸同步控制结构, 如图3 所示。
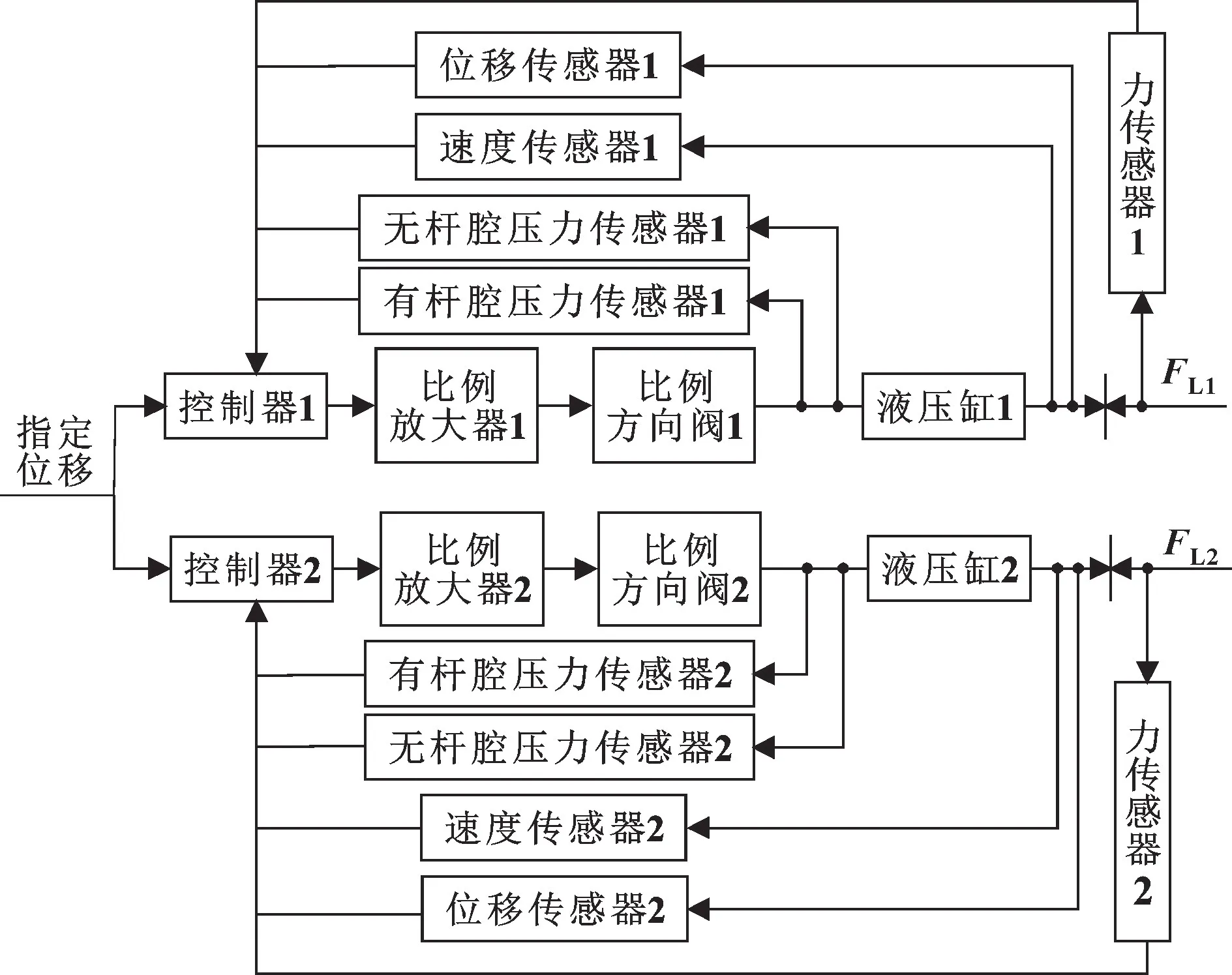
图3 双缸同步控制结构Fig.3 Double-cylinder synchronous control structure
从图3 中可以看出, 给定控制器1 与2 位移信号, 控制器1 与2 将采集力传感器1 与2、 速度传感器1 与2、 位移传感器1 与2、 无杆腔压力传感器1与2、 有杆腔压力传感器1 与2 的信号。 经过反步法计算, 向比例放大器1 与2 施加控制信号, 比例放大器1 与2 将控制信号放大控制比例方向阀1 与2 的动作, 补充或减少液压缸1 与2 油液。
5 联合仿真模型建立
5.1 设置前准备
在建立联合仿真前, 首先需要确定相关设置, 确保联合仿真能够顺利完成[15], 具体如下:
(1) 模型搭建。 根据图1 采用AMESim 软件搭建液压系统模型, 采用Simulink 软件搭建控制器模型,采用S-function 模块将算法封装。
(2) 仿真接口搭建。 根据前面所述, 可以确定液压系统向控制器反馈10 个信号变量, 控制器对液压系统输出2 个控制信号, 根据输入输出信号数量搭建联合接口。
5.2 AMESim-Simulink 联合仿真模型
将设置好的联合仿真接口与AMESim 双缸液压模型和Simulink 控制器模型进行连接, 完成最终的锻造液压机双缸同步控制系统联合仿真模型, 如图4 和图5 所示, 联合仿真主要参数如表1 所示。
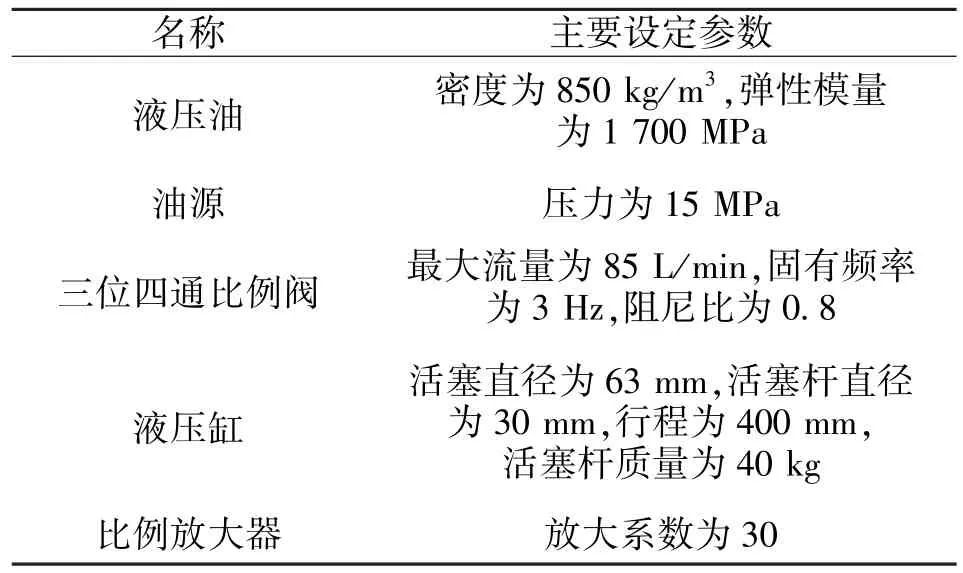
表1 联合仿真主要参数Tab.1 Main parameters of joint simulation
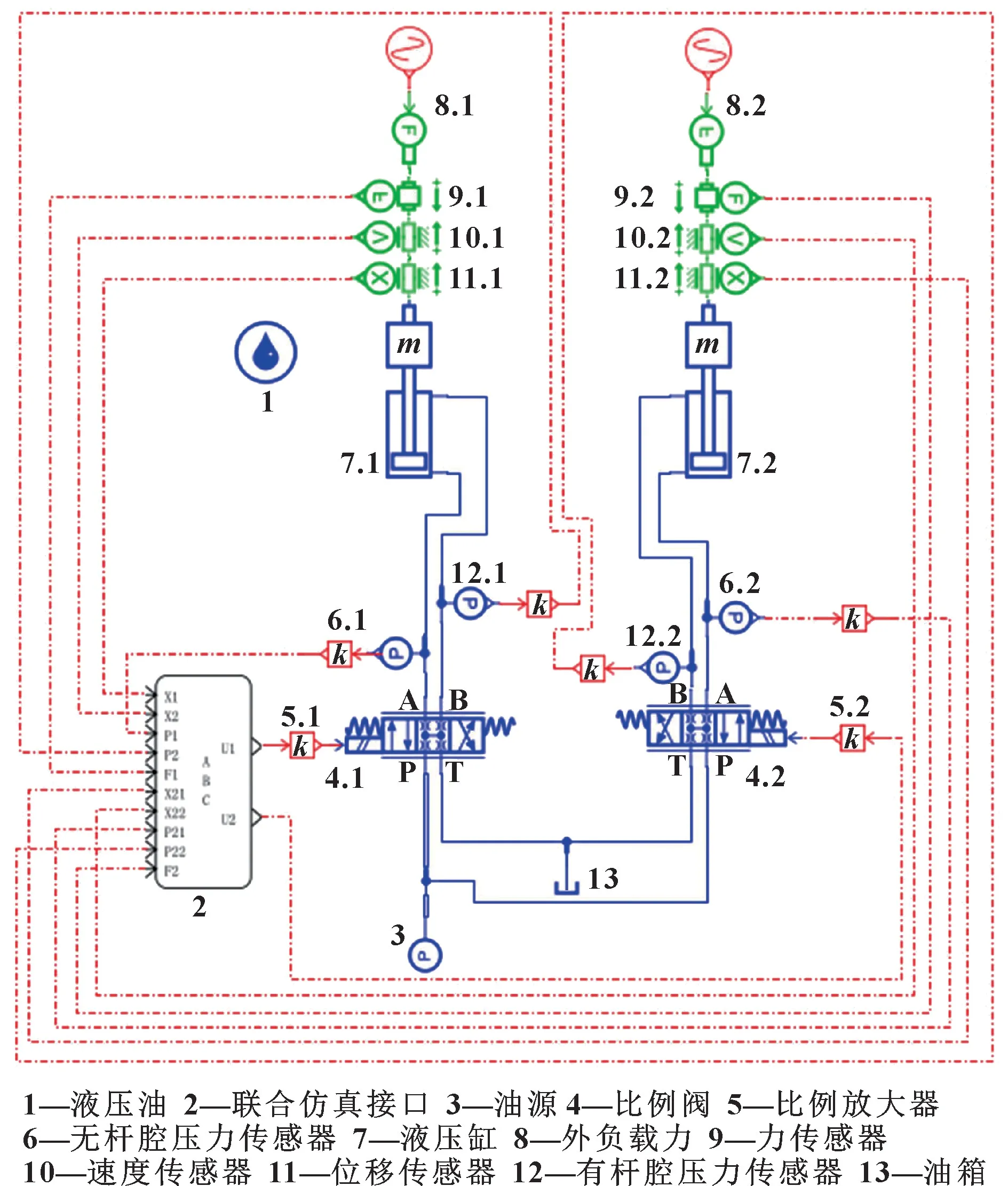
图4 AMESim 仿真模型Fig.4 AMESim simulation model
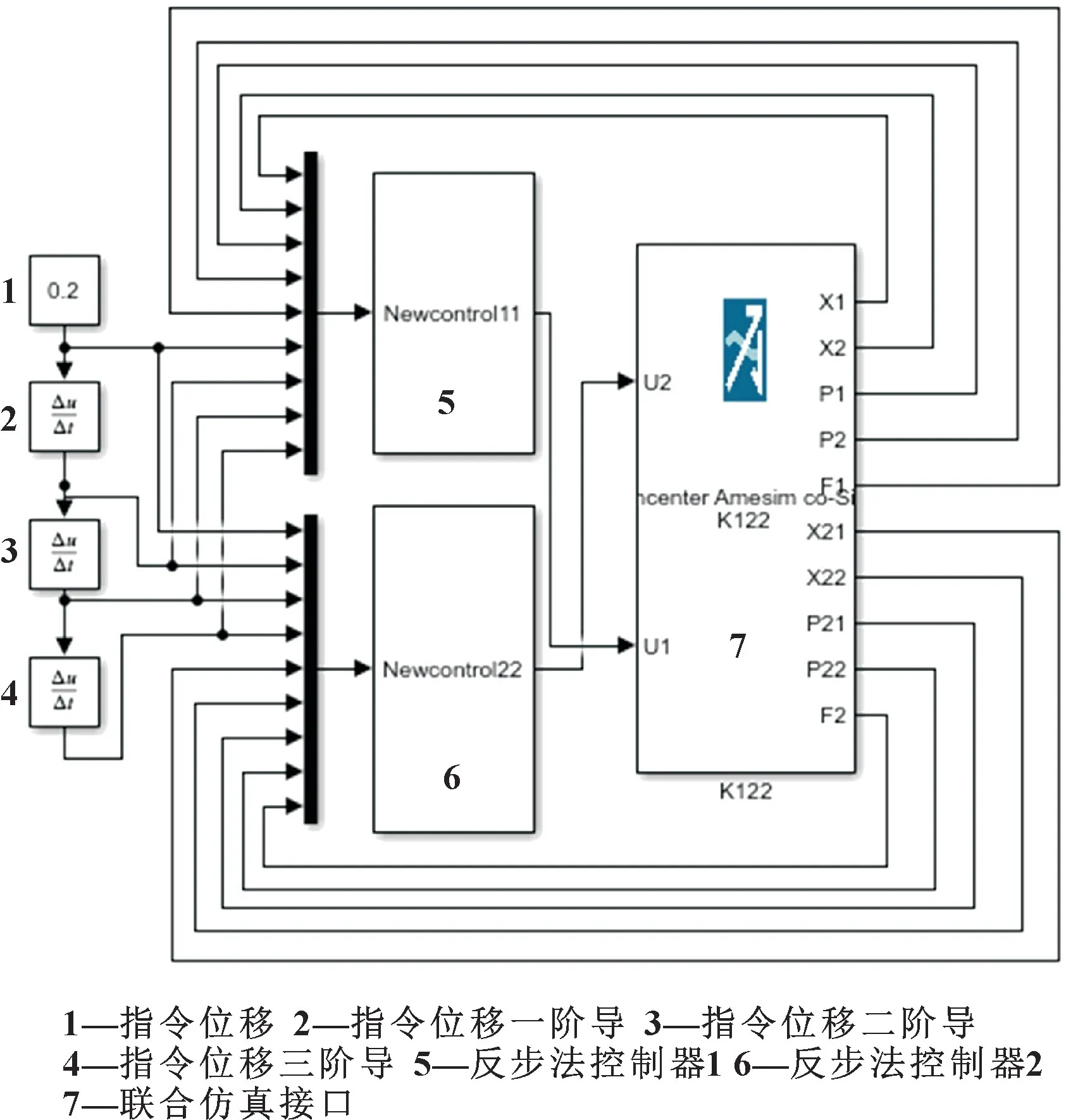
图5 Simulink 仿真模型Fig.5 Simulink simulation model
6 联合仿真
6.1 液压缸位置控制系统数学模型辨识
为了验证反步法控制器的性能, 采用PID 控制器进行对比, 为此需要建立系统输入与输出的数学模型以整定PID 控制器的3 个参数。
采用闭环辨识的方式辨识活塞杆移动至0.2 m 的传递函数, 因仿真软件中获得输入与输出的数据难度较低, 可以采用直接辨识方式, 采集活塞杆0 ~0.2 m、 0.2~0.4 m 内辨识对象输入与输出值, 采集时间为0.001 s。
已知比例放大器放大系数为30, 可以直接得出比例放大器数学模型为
式中:i为电流, A; Δu为输入电压, V。
(1) 比例换向阀传递函数辨识
采集0 ~0.2 m 内输入电流与阀芯位移数据, 将它导入至MATLAB 系统辨识工具箱中进行辨识, 根据文献[4]列举的传递函数结构, 可选择分母阶次为2、 分子阶次为0 的传递函数类型, 运行工具箱得到传递函数为
(2) 比例阀芯位移与液压缸活塞杆传递函数辨识
采集0~0.2 m 内阀芯位移与活塞杆移动速度数据, 将其导入MATLAB 系统辨识工具箱中进行辨识,根据文献[4]列举的传递函数结构, 可选择分母阶次为2、 分子阶次为0 的传递函数类型, 运行工具箱得到阀芯位移与活塞杆速度传递函数, 再乘以积分的时域函数, 得到阀芯位移与活塞杆位移传递函数为
对于液压缸缩回工况, 设置液压缸初始位置为0.4 m, 指令位移给定0.2 m, 采集活塞杆在0.2~0.4 m 内的输入输出值, 辨识方式与活塞杆伸出工况辨识方式相同, 得阀芯位移与活塞杆位移传递函数为
6.2 控制参数设定
首先采用粒子群算法对PID 控制器参数进行整定, 式(36) (37) (38) (39) 参与整定。 系统采用种群规模m=200, 迭代次数n=20, 惯性权重值w=1, 学习因子c1=2, 学习因子c2=2。 以时间误差绝对值积分性能作为参数寻优的适应度函数, 如式(40) 所示:
经过200 粒子的20 次迭代, 可获得液压缸活塞杆2 种状态下参数整定结果, 如表2 所示。
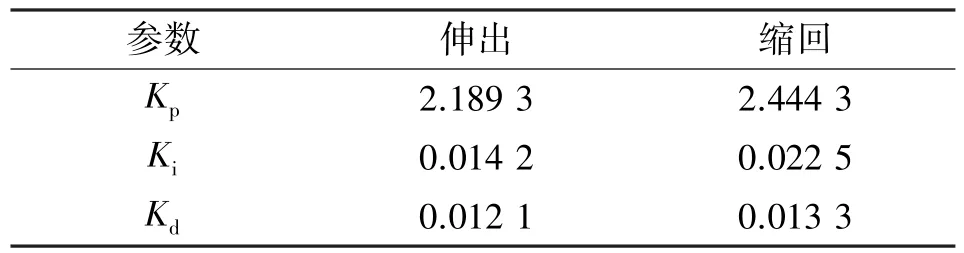
表2 PID 控制器整定参数Tab.2 PID controller tuning parameters
目前对于反步法参数整定的研究较少, 所以此次采用多次调试的方式得出反步法参数, 如表3 所示。
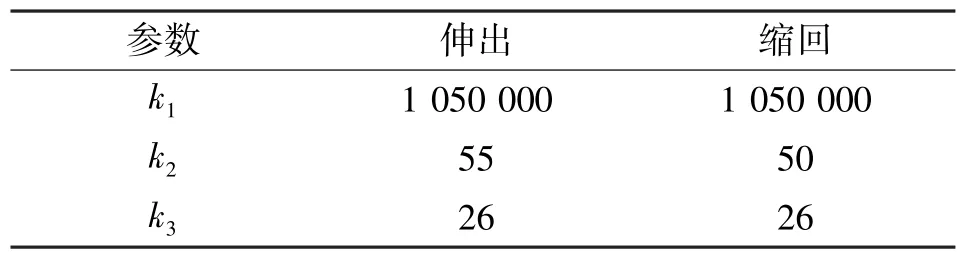
表3 反步法控制器参数Tab.3 Parameters of backstepping controller
6.3 仿真对比
为了验证反步法控制器在双缸同步控制中的性能, 从阶跃响应和正弦响应入手进行仿真测试。
为了测试反步法控制器阶跃响应性能, 给定位移信号0.2 m, 液压缸1 处无外负载力, 对液压缸2 施加4 600 N 的外负载力, 与PID 控制器控制的双缸同步控制仿真模型进行对比, 运行结果如图6—9 所示,仿真结果如表4 所示。
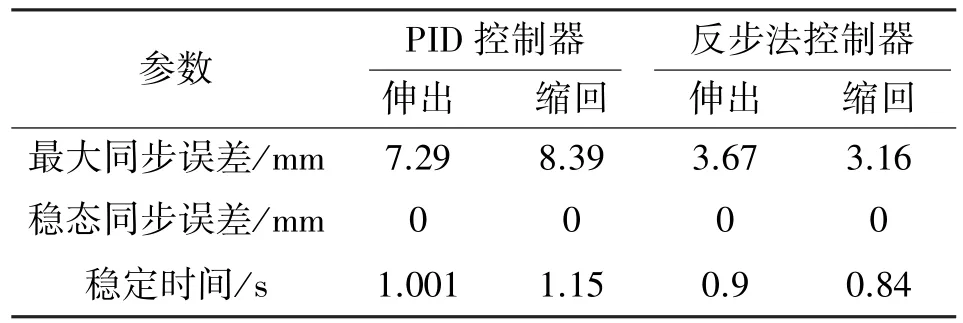
表4 同步控制仿真结果对比Tab.4 Comparison of simulation results for synchronous control
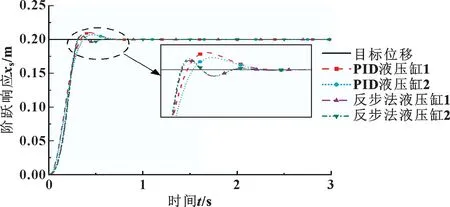
图6 伸出工况阶跃响应曲线Fig.6 Step response curves under extended operating condition
从图6 和图8 中可以看出: 从双缸的超调量与到达指定位置的速度方面讲, 反步法控制器均优于PID控制器; 从同步控制方面讲, 结合图7 与表4 可以得出, 在伸出工况中, 使用反步法控制器的双缸同步控制最大误差比PID 控制器减小了49.7%, 稳定时间减少了10.1%; 结合图9 与表4 可以得出, 在缩回工况中, 使用反步法控制器的双缸同步控制最大误差比PID 控制器减小了62.3%, 稳定时间减少了26.96%,2 种控制器都能将稳态误差控制在0 mm。
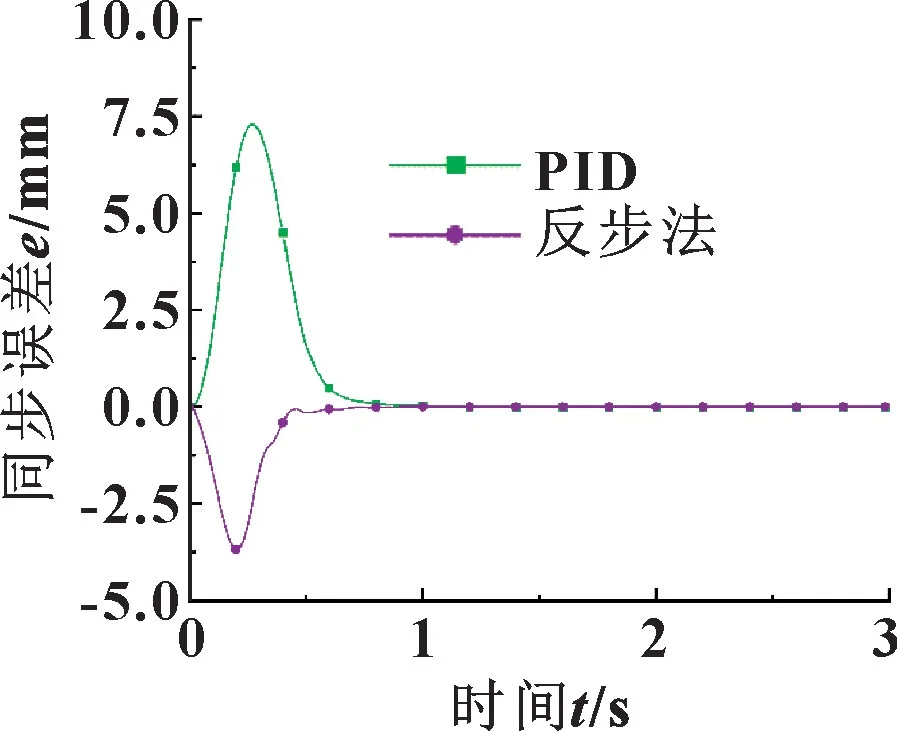
图7 伸出工况同步误差曲线Fig.7 Synchronous error curves under extended operating condition
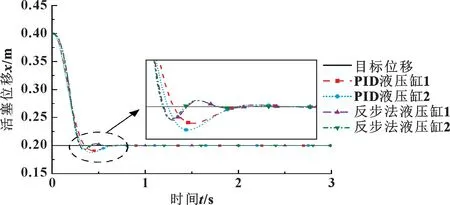
图8 缩回工况阶跃响应曲线Fig.8 Step response curves under retraction condition
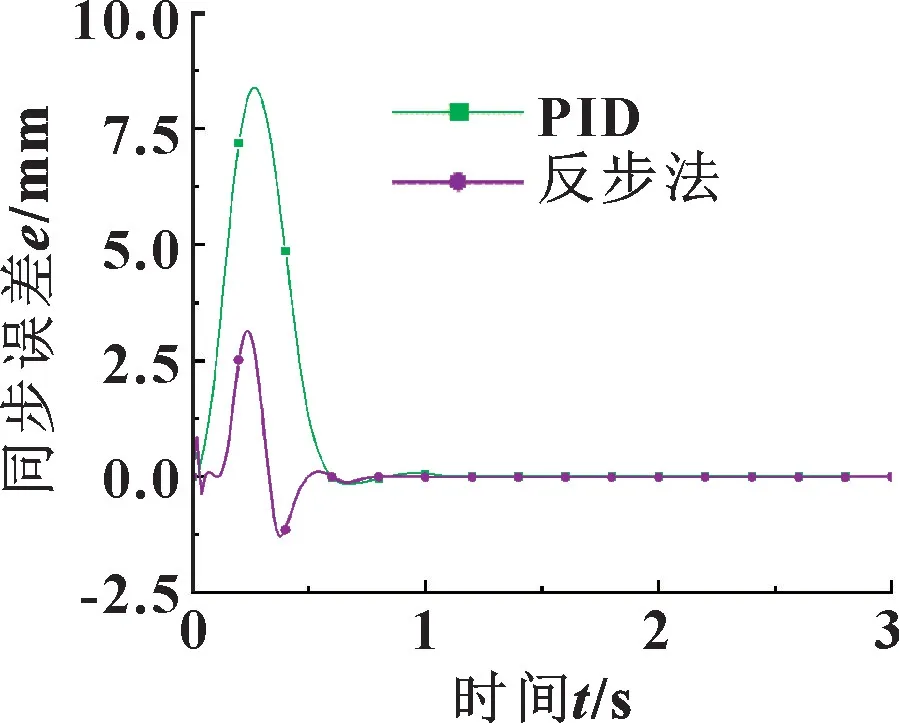
图9 缩回工况同步误差曲线Fig.9 Synchronization error curves of retraction condition
为了测试反步法控制器双缸同步正弦响应性能,给定一个正弦的位置信号, 幅值为0.1 m, 在0.2 m处上下波动, 设定缸1 无外负载力, 缸2 外负载力为4 600 N, 与PID 控制器参与的双缸同步控制仿真模型进行对比, 得出运行结果图10 所示。 可以看出:反步法控制器控制的双缸具有优越的跟踪能力, 其滞后性远远低于PID 控制器。
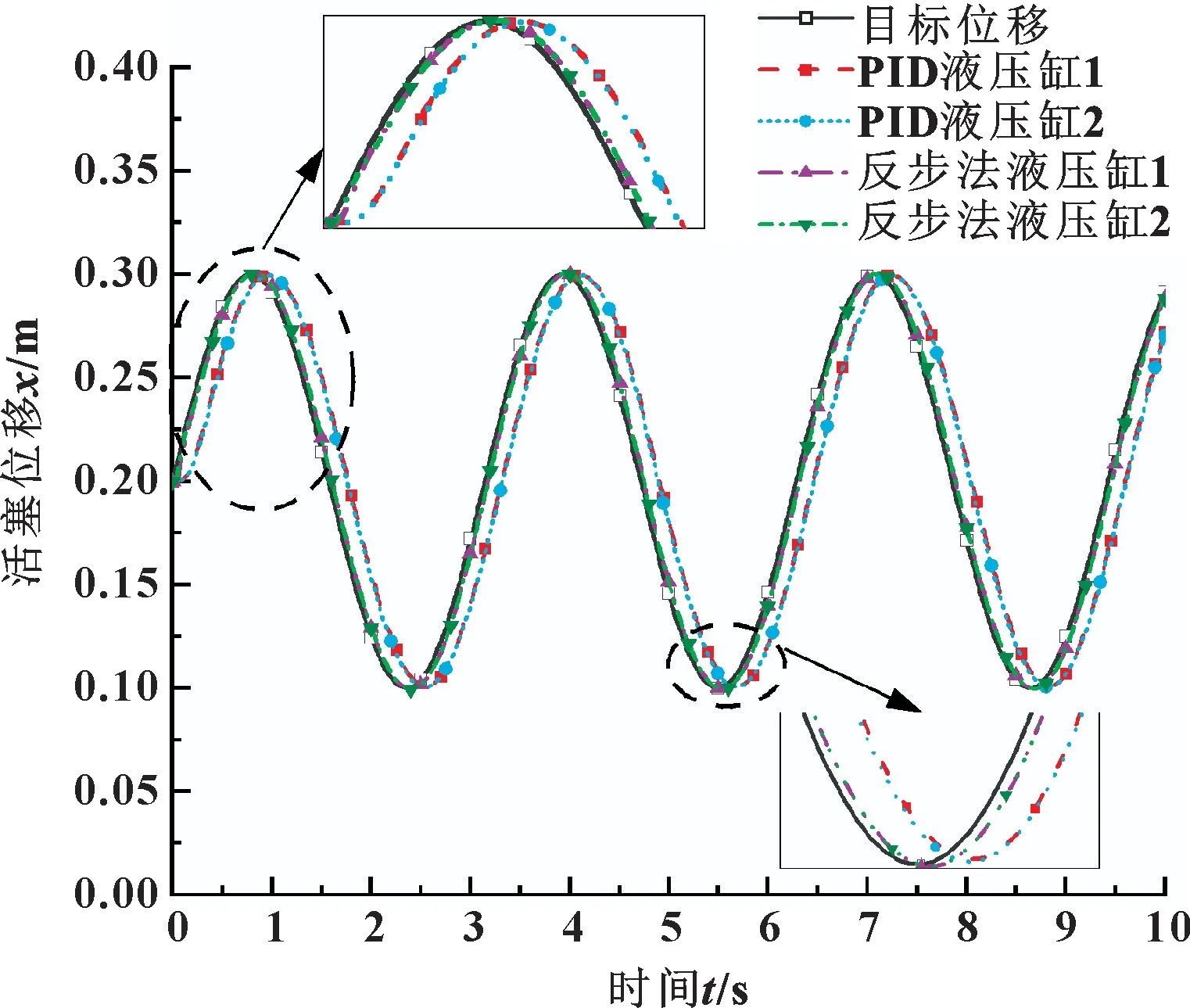
图10 正弦响应曲线Fig.10 Sine response curves
7 结论
为了提高锻造液压机双缸同步控制控制精度, 基于传统双缸同步控制系统, 分析了液压缸位置控制系统运动学模型, 结合Lyapunov 稳定性理论, 设计了基于模型的反步法控制器, 并且应用于并联同步控制结构中, 使用AMESim 与Simlink 联合仿真的方式对反步法控制器与PID 控制器在双缸同步控制中的性能进行对比, 主要得出以下结论: 反步法控制器在双缸同步控制中的表现从阶跃响应方面看, 活塞杆伸出时, 反步法控制器的最大同步误差比PID 控制器最大同步误差减小了49.7%, 调定时间减少了10.1%;在活塞杆缩回时, 反步法控制器的最大误差比PID控制器最大误差减小了62.3%, 调定时间减少了26.96%; 从正弦跟踪能力来看, 相较于PID 控制器,双液压缸滞后性明显降低。 从以上分析对比可以看出, 反步法控制器能够满足双缸同步控制要求。
