改进布谷鸟算法在装配序列规划中的应用研究
2024-03-05秦红斌王玲军唐红涛孔仁杰
秦红斌, 王玲军, 唐红涛, 孔仁杰
(武汉理工大学机电工程学院, 湖北武汉 430070)
0 前言
在制造业中, 产品装配过程所耗费的时间占整个生产时间的20%~50%, 产品的装配成本耗费超过40%[1]。 装配序列规划(Assembly Sequence Planning,ASP) 是产品设计和制造的重要环节, 装配序列的优化对降低生产成本、 提高产品装配质量和生产效率至关重要。 装配序列规划已经被证明是一个典型的NPhard 问题[2-3]。 因此, 国内外的诸多学者对ASP 问题展开大量的研究。 在已有的解决ASP 问题的方法中,智能优化算法展现了其独有的优势。 BONNEVILLE等[4]首次将遗传算法应用于求解ASP 的问题中, 随后蚁群优化算法[5]、 粒子群优化算法[6]等都被应用于求解ASP 问题。
刘冬等人[7]针对基本粒子群算法早熟的缺点, 提出了变种群策略-粒子群优化算法(VPS-PSO) 用于求解ASP 问题, 避免了种群陷入局部最优。 HAN等[8]提出了一种结合共生生物搜索(Symbiotic Organ⁃isms Search, SOS) 和蚁群优化(Ant Clony Optimiza⁃tion, ACO) 的SOS-ACO 算法来计算最优或者接近最优的装配序列。 孟冠军、 杨大春[9]建立遗传-蚁群算法求解ASP 问题, 以加快算法的收敛速度。 任云、刘丹[10]提 出 一 种 将 天 牛 须 搜 索 (Beetle Antennae Search, BAS) 算 法 和 闪 电 搜 索 算 法 (Lightning Search Algorithm, LSA) 混合的BAS-LSA 混合算法,结合天牛须算法较优的局部搜索能力和闪电搜索算法较优的全局搜索能力, 提高了求解精度。 但上述研究仍存在以下不足: 在建立装配关系模型时未考虑零件之间的支撑关系, 或者在建立适应度函数时未考虑待装配零件与所有已装配好的零件之间的装配关系。 布谷鸟优化算法(Cuckoo Search, CS) 是由YANG 和DEB[11]提出的一种群智能优化算法, 也是一种新型元启发式算法。 布谷鸟算法结构简单、 算法参数少、易于实现, 兼备较优的全局搜索和局部搜索能力。 雍升[12]将布谷鸟算法运用到求解ASP 问题上, 但是群体中每只布谷鸟都执行Lévy 飞行, 并且飞行步长是一个定值, 缺乏自适应性, 导致收敛速度变慢。 针对以上问题, 本文作者建立考虑装配序列的几何可行性、 稳定性、 聚合性、 重定向性的装配关系模型和适应度函数, 提出一种改进布谷鸟算法 (Improved Cuckoo Search, ICS), 设计编码方案, 改进种群初始化和种群进化策略, 加快解的收敛速度, 使其具有较强的寻优能力。
1 装配关系模型及适应度函数构建
产品的装配序列有多种方案可供选择, 装配序列会影响装配成本和装配效率, 在评价装配序列的优劣时, 应首先考虑装配序列的几何可行性, 即装配序列在几何空间内可进行装配, 再综合考虑装配序列的稳定性、 聚合性、 重定向性。
1.1 装配序列的几何可行性
几何可行性是指在装配体中装配零件Pi时, 已装配好的零件是否对零件Pi产生干涉。 通常情况下,零件是按d(k)={+x,-x,+y,-y,+z,-z}6 个装配方向中一个方向进行装配的, 建立零件在6 个方向的干涉矩阵[13], 如式(1) 所示:
其中:pij表示零件Pj沿k方向装配时与零件Pi的干涉情况, 若pij=1, 表示零件Pj沿k方向装配时与零件Pi发生干涉; 若pij=0, 则无干涉。 矩阵如式(2) 所示:
定义Iik为零件Pi沿k方向装配时与已装好的零件的干涉值之和, 若Iik=0, 则零件Pi可以沿k方向进行装配, 否则, 不能沿k方向进行装配。Iik的计算公式如式(3) 所示:
对于一个装配序列, 若V1=0, 则证明装配体中所有零件都无干涉, 为可行装配序列; 若V1≠0, 则证明为几何不可行装配序列。
1.2 装配序列的稳定性
稳定性包含2 个方面: (1) 零件之间的连接稳定性, 通过建立连接矩阵来表示装配体中各零件之间的连接关系, 用于判断连接稳定性; (2) 零件在装配过程中重力方向上的支撑稳定性, 通过建立支撑矩阵来表示零件之间支撑关系。 装配序列稳定性的量化指标V2的计算公式如式(5) 所示:
其中:V21表示装配序列连接稳定性的量化指标;V22表示装配序列支撑稳定性的量化指标。
(1) 连接稳定性。 各零件之间的连接关系用连接矩阵C= [cij]n×n表示, 元素cij表示零件Pi与零件Pj之间的连接类型。 定义cij的值如式(6) 所示:
接触连接关系表示零件之间相互接触, 稳定连接表示两零件之间通过连接件连接, 具备稳定的连接关系。
装配序列连接稳定性指标V21的求解算法如下:
①参数初始化, 令V21=0,S1=0,S1为算法计算中间变量;
②从连接矩阵C中取出零件Pi与前i-1 个已装配好的零件连接信息, 并将它置于N1中,N1为算法临时存储信息的变量;
③若N1存在值为0, 则S1=0, 若不存在, 则判断N1中是否存在1, 若存在, 则S1=1, 若不存在,则判断S1=2;
④V21=V21+S1;
⑤i=i+1, 如果i<n, 转至步骤②; 否则转至步骤⑥;
⑥结束。
由上述可知:V21的数值越小, 代表装配过程中稳定连接越多, 装配过程中的稳定性越好。
(2) 支撑稳定性。 各零件之间的支撑关系用矩阵M= [mij]n×n表示, 元素mij表示零件Pi与零件Pj之间的支撑类型。 定义mij的值如式(7) 所示:
装配序列支撑稳定性指标V22的求解算法如下:
①参数初始化, 令V22=0,S2=0,S2为算法计算中间变量;
②从支撑矩阵M中取出零件Pi与前i-1 个已装配好的零件支撑信息, 并将它置于N2中,N2为算法临时存储信息的变量;
③如果N2存在值为0, 则S2=0; 否则,S2=1;
④V22=V22+S2;
⑤i=i+1, 如果i<n, 转至步骤②; 否则转至步骤⑥;
⑥结束。
由上述可知:V22的数值越小, 则代表装配过程中在重力方向的支撑越多, 装配稳定性越好。
1.3 装配序列的聚合性
聚合性表示装配过程中零件装配工具的改变次数, 在装配过程中应该尽可能地减少装配工具的改变次数, 有助于降低装配成本。 装配工具的改变定量计算如式(8) 所示:
装配过程中装配工具的改变次数V3越小, 装配序列的聚合性越好, 装配序列越优。
1.4 装配序列的重定向性
重定向性是指在装配过程中零件装配方向的改变次数, 装配过程中应降低装配方向的改变次数, 提高装配效率。 装配方向的改变定量计算方式如式(9)所示:
装配过程中装配方向的改变次数V4越小, 装配序列的重定向性越好, 装配序列越优。
1.5 适应度函数构建
综上所述, 综合考虑装配序列的几何可行性、 装配序列的稳定性、 装配序列的聚合性、 装配序列的重定向性4 个评价指标, 通过量化方法建立适应度函数, 如式(10) 所示:
其中:ωi(i=1, 2, 3, 4) 为权重系数;V1、V2、V3、V4分别表示装配序列的几何可行性、 稳定性、 聚合性和重定向性评价指标。 适应度值F越小,装配序列越好。
2 改进布谷鸟算法求解ASP 问题
2.1 标准布谷鸟算法

基于被发现概率Pa来淘汰更新后的解, 采用随机游走的局部搜索策略生成相同数量的解补充种群,保持种群数量的一致, 如式(17) 所示:

2.2 编码与解码
标准布谷鸟算法适用于求解连续性问题, 而装配序列规划问题是离散型, 无法直接应用求解。 为此,文中采用随机键和最小位置规则(Smallest Position Value, SPV) 的方法, 对编码方式进行处理, 从而建立起个体与装配序列的映射关系。 如图1 所示,SPV 规则为原向量的每个元素生成随机值, 原向量的元素根据随机值的大小经过升向排序, 得到一个新向量。
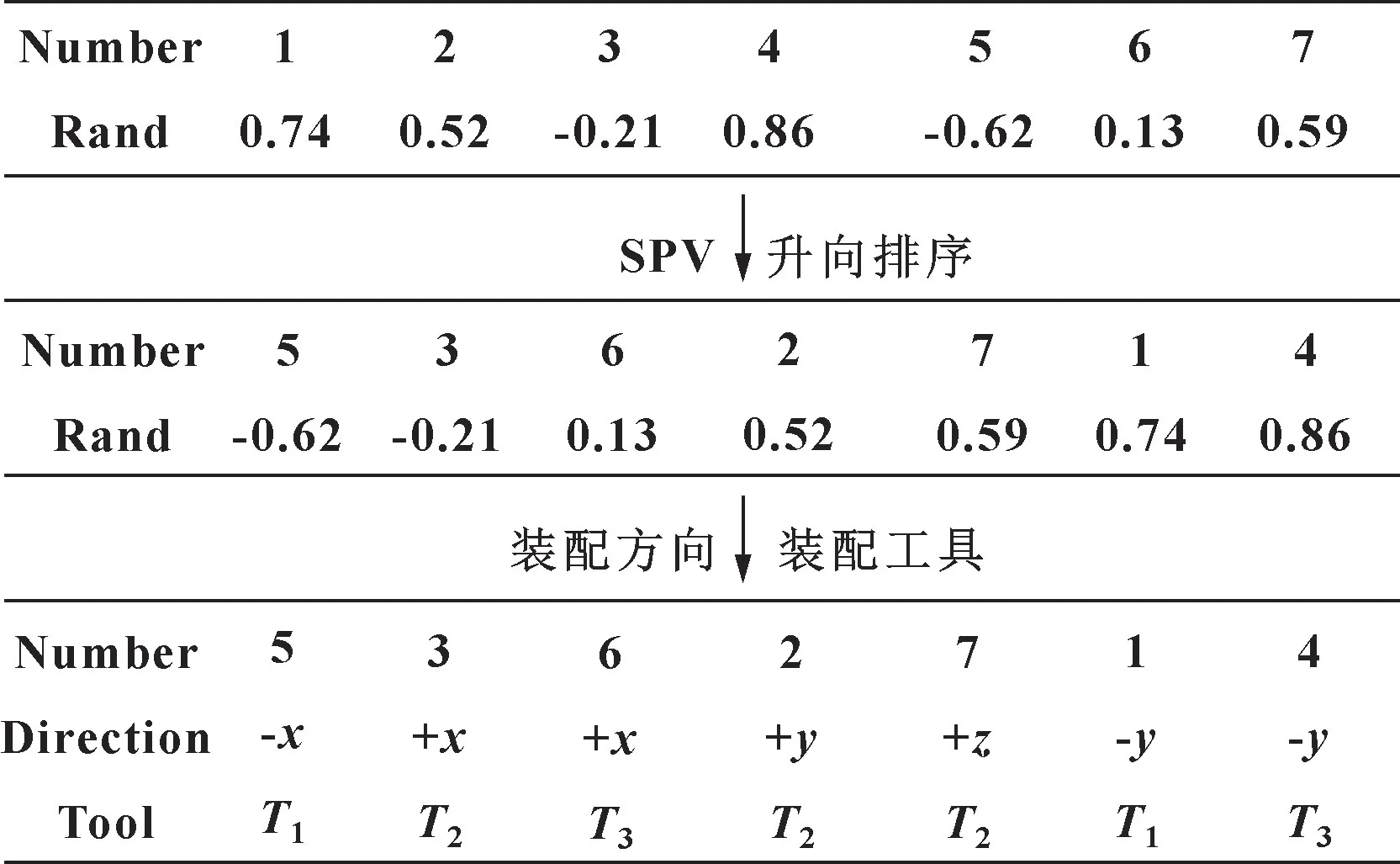
图1 编码过程Fig.1 Encoding process
ASP 问题涉及多零件的装配顺序、 装配方向选择、 装配工具选择问题, 因此, 文中采用基于零件编号、 装配方向、 装配工具的3 层编码规则。 编码时首先生成零件编号序列(Number), 然后根据所生成的零件编号序列对零件的装配方向(Direction)、 装配工具(Tool) 进行选择。 装配方向、 装配工具层用于记录该条装配序列的装配信息。件4 的装配方向也为+y。 如果后续零件的可行装配方向无法与前一位保持一致, 例如零件2 中可行装配方向没+y, 则考虑后续零件5 的可行装配方向, 选择零件2 的装配方向为+x, 同理可得零件5 和零件1 的装配方向分别为+x、+x, 该装配序列的装配方向分别为{+y,+y,+x,+x,+x} 。 装配工具与装配方向的选择机制一样, 可得该装配序列的装配工具分别为{T3,T3,T3,T1,T3} 。
结合编码过程可得: 零件装配顺序为5→3→6→2→7→1→4, 装配方向分别为{- x,+x,+x,+y,+z,-y,-y} , 装配工具分别为{T1,T2,T3,T2,T2,T1,T3} 。
2.3 混合种群初始化策略
为了提高初始化种群的质量和保证种群的多样性,文中设计了混合种群初始化策略进行种群的初始化(包括几何不可行序列), 即: (1) 基于最大化可行序列和最小装配成本的种群初始化; (2) 随机初始化策略。 2 种策略生成的初始化种群数量分别为50%。
文中的编码采用基于零件编号、 装配方向、 装配工具的3 层编码, 在装配模型评价指标中, 装配序列的几何可行性、 稳定性评价指标在零件编号层确定后, 就可以通过对应的算法计算出来。 最大化可行序列和最小装配成本策略体现在对装配方向和装配工具的合理选择上, 随机策略则是对零件的装配方向和装配工具进行随机选择。 如图2 所示, 有装配序列3→4→2→5→1, 装配方向层为此零件与前一个零件不发生干涉的可装配方向, 装配工具层为此零件装配时所需要使用的工具。

图2 优化策略Fig.2 Optimizing strategy
在为首位零件选择装配方向和装配工具时应考虑对后一位零件的影响, 如为零件3 选择时装配方向应在{- x,+y,+z,-z} 中随机选择。 现随机选为+y方向, 后续选择零件的装配方向应尽量在满足装配几何可行性的前提下和前一位的零件保持一致。 零
2.4 改进的种群进化策略与搜索策略
在布谷鸟算法中, 群体中每只布谷鸟都执行Lévy 飞行, 会造成收敛速度变慢, 并且标准Lévy 飞行中的步长是一个定值, 缺乏自适应性, 同样会导致收敛速度变慢。 针对此种情况, 文中将布谷鸟种群分为3 个子群, 分别采用不同的种群进化策略, 按种群的适应度值进行升序排序。 首先取出适应度较差的1/3 种群数量的布谷鸟作为一个子群, 采用交叉、 变异的方式来代替Lévy 飞行进行更新, 其中交叉相当于Lévy 飞行的“长飞行”, 在全局的范围内进行搜索; 变异相当于Lévy 飞行中的“短飞行”, 在局部范围进行搜索, 可以减少Lévy 飞行的次数, 加快收敛速度; 然后再将剩下的种群随机分为2 个子群, 分别采用固定步长的标准Lévy 飞行和基于自适应步长的改进Lévy 飞行进行种群更新; 最后将更新后的3 个子群合并生成的新一代种群。
采用部分匹配交叉(Partially-Matched crossover,PMX) 的方式进行交叉操作[14], 具体操作流程如图3 所示。
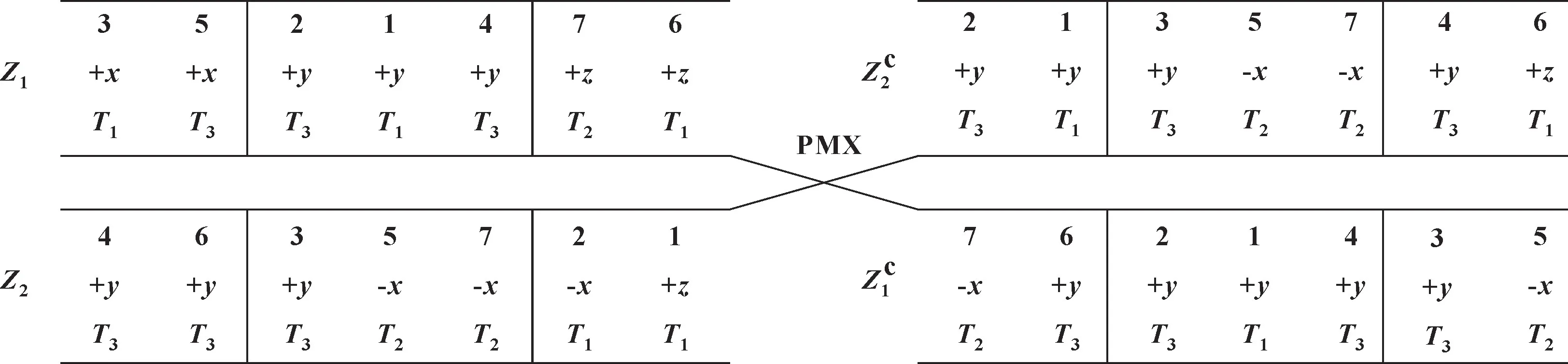
图3 PMX 交叉操作Fig.3 PMX crossover operation
从种群中随机抽取2 个个体Z1和Z2作为父代,首先随机选取2 个交叉的点, 将2 个点之间的部分进行交叉, 再将剩余的部分采用复制或相匹配的方式进行交叉替换。 如图3 所示, 父代Z1中214 被选中,父代Z2中357 被选中, 那么2 与3、 1 与5、 4 与7 相匹配。 首先将214 与357 分别加入子代Z和子代Z中, 再将其他位置上的编号复制到子代中, 若子代中已经存在此编号, 则运用匹配规则将匹配后的编号复制到子代中, 从而得到新的子代。
采用随机选取2 个零件位置进行互换的变异操作方式, 具体操作如图4 所示, 随机选取的第一个是位置2, 第二个是位置6, 将位置2 与6 的零件编号互换, 从而得到新的个体Zf2。
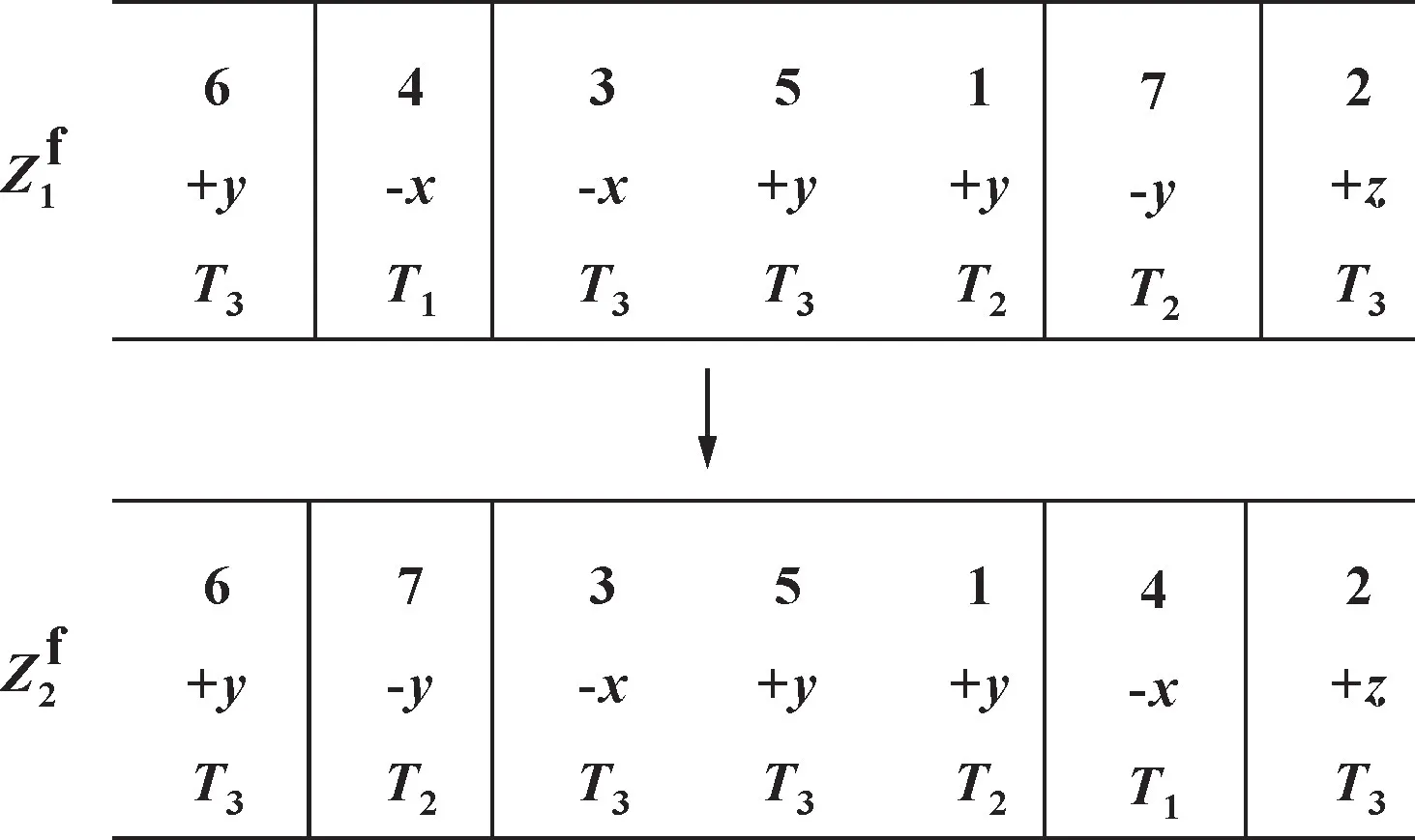
图4 互换变异操作Fig.4 Swap mutation operation
通过算法的迭代次数控制飞行步长: 在算法初期, 应进行较大步长的Lévy 飞行, 有助于提高全局搜索能力, 避免陷入局部最优; 在算法后期, 应进行较小步长的Lévy 飞行, 有助于提高搜索精度。 文中步长因子α的取值如式(18) (19) 所示[15]:
其中:αmax表示步长因子的最大值;αmin表示步长因子的最小值;t为当前迭代次数;T为迭代总次数。 经文献[15]实验验证,αmax取0.5、αmin取0.05效果最佳。
2.5 ICS 算法流程
改进布谷鸟算法流程如图5 所示, 具体步骤如下:
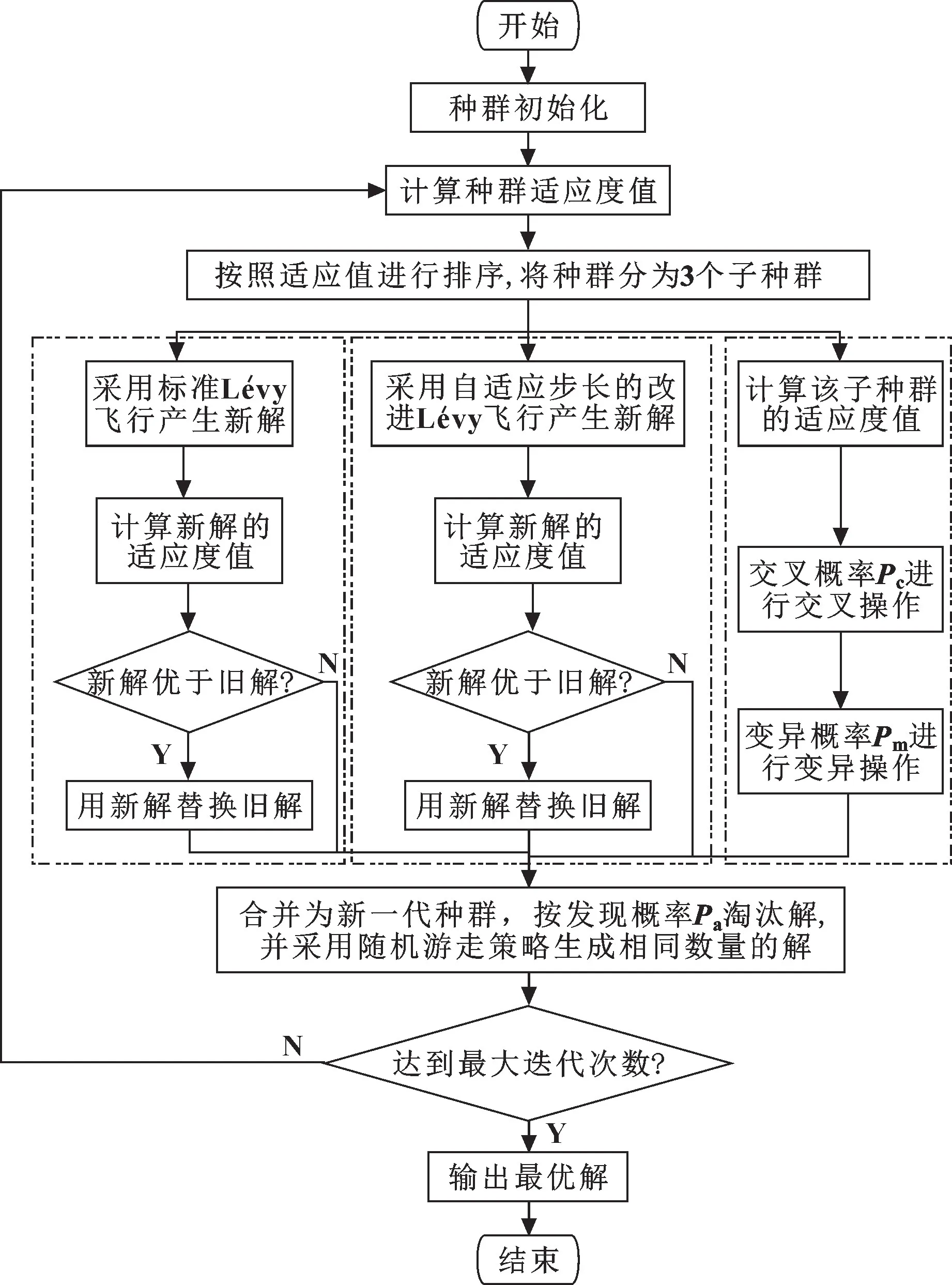
图5 ICS 算法流程Fig.5 ICS algorithm flow
步骤1, 对算法相关参数进行初始化, 包括种群数量n, 最大迭代次数T, 发现概率Pa, 交叉概率Pc, 变异概率Pm, 适应度函数权值系数ωi(i=1, 2,3, 4);
步骤2, 采用上述混合种群初始化策略初始化种群;
步骤3, 按照种群适应度值对种群进行升序排序, 首先取出适应度较差的1/3 种群数量的个体作为一个子种群, 再将剩下的种群平均分为2 个子种群;
步骤4, 将适应度较差的子种群采用交叉、 变异的方式进行种群更新, 剩余的2 个种群分别采用标准Lévy 飞行和基于自适应步长的改进Lévy 飞行进行种群更新;
步骤5, 将采用3 种更新方式得到的新一代种群合并为新的种群, 按发现概率Pa来淘汰更新后的解,采用随机游走策略生成相同数量的解;
步骤6, 判断是否达到最大迭代次数T, 如果未达到, 转至步骤3; 否则, 转至步骤7;
步骤7, 输出种群最优解。
3 实例应用与分析
为了验证文中所提出的ICS 算法求解ASP 问题的有效性, 现以某液压产品制造企业所生产的锁紧机构齿条缸为实例进行验证。 将一组标准件作为一体化零件进行考虑, 则该装配体有24 个零件, 如图6 所示。

图6 锁紧机构齿条缸Fig.6 Locking mechanism rack cylinder
采用MATLAB 2017b 编程软件实现改进布谷鸟算法(ICS), 为了验证改进布谷鸟算法的优越性, 将它与标准布谷鸟算法(CS)[12]、 遗传算法(Genetic Algorithm, GA)[4]、 粒 子 群 算 法 (Particle Swarm Optimization, PSO)[16]进行对比。 改进布谷鸟算法的参数设置为: 最大迭代次数T=200, 种群规模N=90, 交叉概率Pc=0.8, 变异概率Pm=0.2, 发现概率Pa=0.3。 对比算法参数的设置参考相应文献。 改进布谷鸟算法采用文中所提出的混合种群初始化策略, 对比算法均采用随机初始化策略。
图7 给出了某次迭代过程中改进布谷鸟算法与其他3 种算法在求解ASP 问题中适应度值与迭代次数的收敛曲线, 图8 给出了每代适应度平均值与迭代次数的收敛曲线。 可以看出: 基于优化最大化可行序列和最小装配成本的种群初始化策略的改进布谷鸟算法的初始解质量明显优于其他3 种采取随机初始化的算法。 并且, 改进布谷鸟算法的收敛速度和求解质量亦更优。 改进布谷鸟算法的最优适应度值最小(5.25), 在寻优能力上有较大的优势。 改进布谷鸟算法获得最优的可行序列为零件3→零件17→零件4→零件2→零件1→零件14→零件16→零件19→零件21→零件22→零件12→零件15→零件13→零件9→零件7→零件11→零件10→零件8→零件6→零件5→零件18→零件23→零件24→零件20。
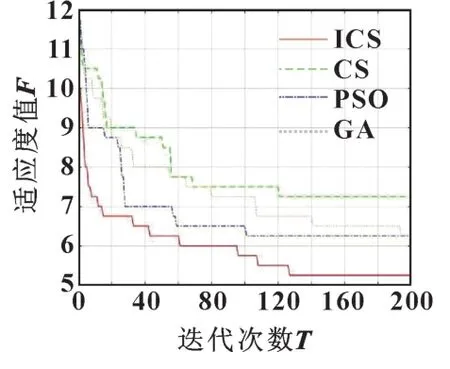
图7 适应度值算法迭代Fig.7 Fitness value algorithm iteration
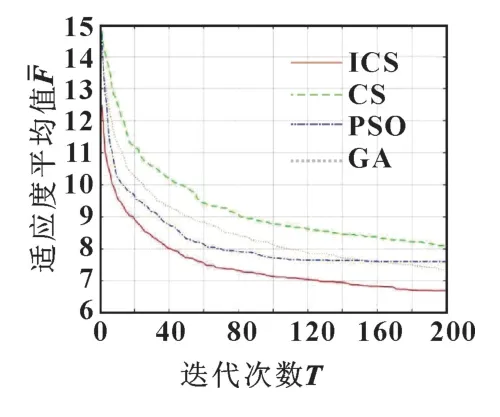
图8 适应度平均值算法迭代Fig.8 Fitness mean algorithm iteration
4 结论
为了求解装配序列的规划问题, 文中建立了考虑装配序列的几何可行性、 稳定性(连接稳定性和支撑稳定性)、 聚合性和重定向性评价指标的装配关系模型和适应度函数。 针对标准布谷鸟优化算法在求解ASP 问题时收敛速度慢的问题, 对布谷鸟算法进行改进, 根据模型的特点设计了混合种群初始化策略, 改进了种群的进化策略。 最后以锁紧机构齿条缸为实例, 验证了所提出的改进布谷鸟算法的可行性, 结果表明: 改进布谷鸟算法加快了算法的收敛速度, 具备较强的全局搜索能力和寻优能力, 能有效地应用到求解装配序列规划问题上。
