复杂纹理工件的位姿检测方法研究
2024-03-05刘建春刘轩蒋炳翔李伟
刘建春, 刘轩, 蒋炳翔, 李伟
(1.厦门理工学院机械与汽车工程学院, 福建厦门 361024; 2.厦门市机器人系统与数字制造重点实验室, 福建厦门 361024; 3.厦门航天思尔特机器人系统股份公司, 福建厦门 361023)
0 前言
刚性物体的位姿检测是一个工业应用场景下质量检测和机器人控制的重要问题[1]。 在工业生产过程中, 部分工件对组合拼装的精度有较高要求, 机器人通过人工示教或视觉识别的方法抓取工件的过程中,由于受机器人自身误差和抓取点定位误差的影响, 机器人将工件移动到指定坐标后, 工件的实际三维姿态会产生细微的偏差[2], 这些姿态偏差会对工件的安装精度造成影响。
视觉检测技术在效率、 成本和稳定性上都有较为显著的优点, 目前, 位姿检测多基于视觉检测方法。牛晨等人[3]利用双目视觉结合SURF 算法, 实现箱体的三维位姿检测, 这种方法适用于边缘纹理稳定的物体, 而对于金属工件, 其表面纹理易受环境光和表面粗糙度的干扰。 高翔等人[4]针对工件摆放误差与拼装误差的问题, 利用多个线激光器采集工件若干边缘点坐标, 但是线激光器的安装位置与测量点需要根据工件的外形调整, 且激光器的位置不可随意变动, 难以同时测量不同形状的工件。 陈艺海[5]利用双目视觉结合光栅条纹对物体进行三维重建, 再将重建模型与理想点云模型做三维配准, 得到物体的三维位姿, 这种方法重建与匹配的计算量较大, 且金属工件的边缘部分重建效果并不稳定, 需要被测工件具有更明显的三维特征信息才便于点云配准。 近年来, 深度学习技术的发展也为物体位姿估计研究提供了新的思路[6]。PENG 等[7]提出PVNet, 根据提取指向物体关键点的方向向量判断物体位姿。 HE 等[8]提出全流双向融合FFB6D 网络, 根据单个RGB-D 图像进行6D 姿态估计, 利用RGB 图像中的外观信息和深度图像中的几何信息作为2 个互补数据源, 但是这2 种方法都依赖对象有较为稳定的二维纹理信息, 而部分利用点云的方法如PointNet[9], 则要求获取较为准确的点云数据, 这对表面质量复杂的金属工件来说具有一定困难。
在工业应用场景下, 部分金属工件三维形状特征匮乏, 只有简单的平面特征, 且其表面的纹理又易受锈迹和加工工艺的影响, 表面粗糙度不均匀, 即使是同种工件, 其纹理也各有差异, 易受环境光干扰, 较为复杂, 不利于提取稳定的特征点。 基于上述情况,为解决这类带有平面特征的复杂纹理金属工件位姿检测的问题, 本文作者提出一种可以灵活适应多种类型工件的三维位姿检测方法, 实现对工件三维位姿的检测。
1 系统设计
1.1 系统平台设计
该方案采用主动投射非编码多线结构光的方式,检测系统由2 台工业相机与DLP 投影仪组成。 相机选用1 200 W 黑白相机, 镜头焦距为25 mm, 工作距离L为400 mm, 结合相机在蓝光波段的量子效率曲线, 选用波长为459 nm 的DLP 投影仪和对应蓝光波长的带通滤光片。
与传统多线激光器和网格激光器相比, DLP 投影仪可更灵活地调节结构光的形状、 间距和密度, 具有较高的自由度, 可以灵活适应不同工件的检测需求。 系统工作平台如图1 (a) 所示。

图1 系统工作平台(a) 和待测工件(b)Fig.1 System working platform (a) and target workpiece (b)
投影仪处于2 个相机中间, 2 个相机的光轴以夹角θ对准被测物体, 在检测不同的工件时, 投影仪分别向被测工件投射预先绘制的多条竖直结构光, 双目相机依次采集投射图案, 完成后续检测流程。 待测工件如图1 (b) 所示, 可见该类工件三维特征较少,工件表面同时存在粗糙部分与易反光的部分, 且位置分布随机, 表面纹理质量较为复杂。
1.2 双目测距原理
双目相机在进行立体标定后[10], 对拍摄图像做极线校正, 使左右相机的光轴“虚拟” 平行。 极线校正后的双目视觉模型如图2 所示。
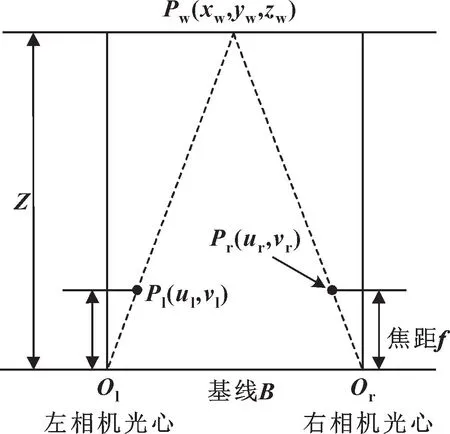
图2 双目视觉模型Fig.2 Binocular vision model
校正后左右照片的同一特征点在行方向上对齐,便于后续对空间点进行三维重建。 设Pw(xw,yw,zw)是空间中的一点,Z是Pw在相机坐标系下的深度值,该点在左右相机成像面上的坐标分别是Pl(ul,vl)与Pr(ur,vr), 相机焦距为f, 左相机光心Ol与右相机光心Or的距离B为相机基线, 可由双目标定获得。设世界坐标系与左相机坐标系重合, 由相似三角形原理可得:
其中:ul-ur即为空间点P在双目相机成像面上的视差。 因此, 左右成像面上的同一空间点, 均可以通过式(1) 实现对该点的三维重建。
2 工件位姿检测算法
该方案的研究路线为: DLP 投影仪向待测工件表面分别投射差分多线结构光, 双目相机采集图片,并分别计算出2 次投射的多线结构光中心线。 对同一侧相机采集的图片, 由2 条中心线相互补偿, 拟合出一条虚拟的新中心线。 再由两侧各自拟合的新中心线, 以线序和特征点行坐标的顺序, 依次提取左右照片中新中心线上的立体匹配点并进行三维重建。 随后, 利用基于Tukey 权重函数的平面拟合方法与直线拟合方法, 求解被测面的法向量, 提取工件的若干边缘和角点坐标。 最后, 将边缘点和角点坐标映射到拟合平面上, 实现对工件的三维位姿检测。 研究路线如图3 所示。
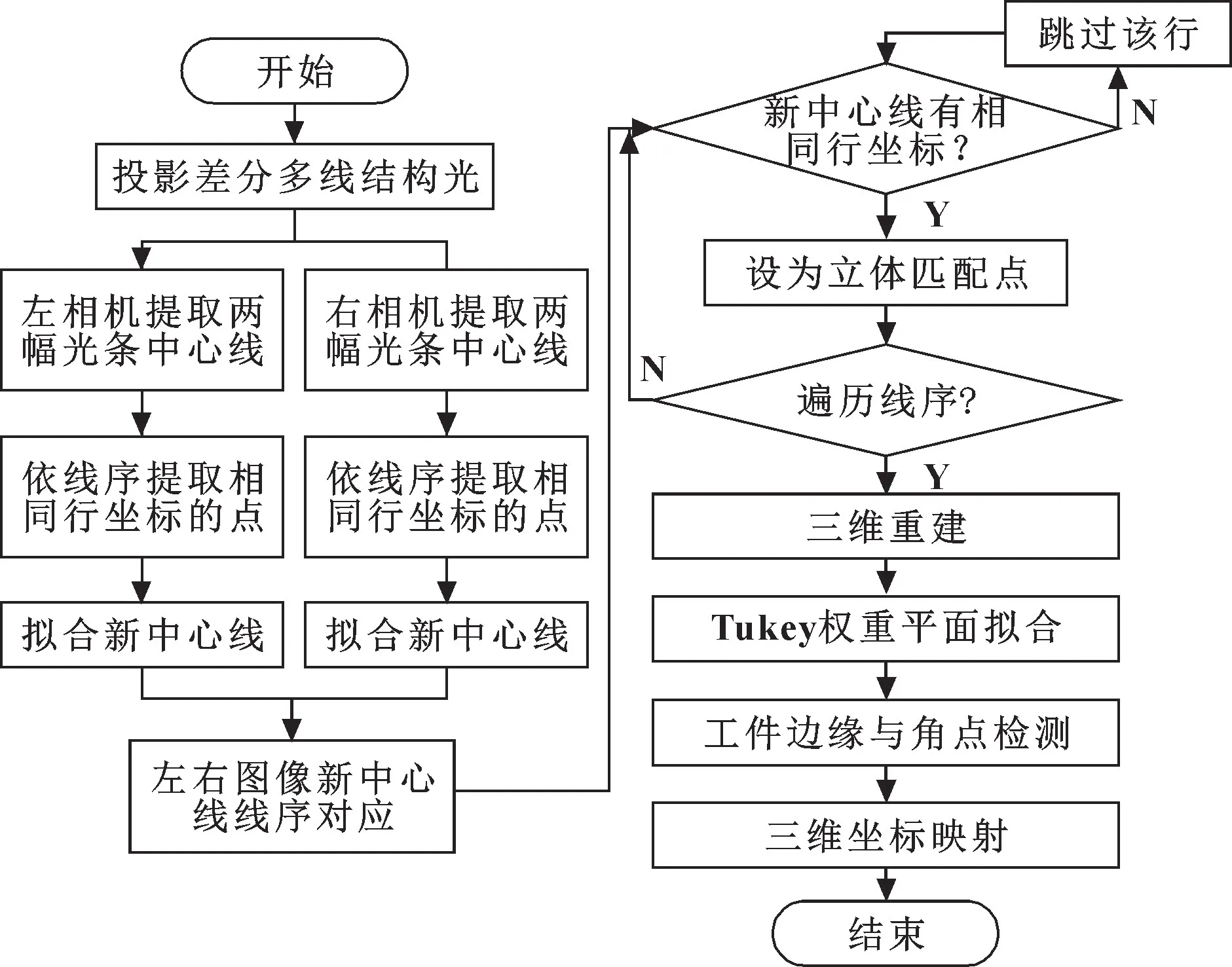
图3 研究路线流程Fig.3 Flow of research roadmap
2.1 基于差分多线结构光的平面特征点提取方法
目前提取光条中心线的方法有灰度重心法、 形态学骨架法和极值法等[11], 然而受工件表面粗糙度的影响, 实际拍摄的光条极易受反光干扰, 或遇到光条灰度值局部异常的缺陷, 上述算法极易受到这些缺陷的影响, 降低提取中心线的质量。 而Steger 算法常用于检测图像中的线条, 该算法可以将光条的截面光强分布转变为理想的正态函数, 并补偿灰度值非对称的光条, 校正待提取光条的位置与宽度, 有较好的抗干扰能力[12], 因此选用Steger 算法初步提取光条中心线。
设图像的灰度分布函数为I(x,y), 利用Hessian矩阵[12]计算光条图像中每个点附近的光强度特征向量, 并以沿着光强变化最快的方向对像素灰度做泰勒多项式展开, 进而计算出光条中心的亚像素位置。 对于二维高斯函数G(x,y), Hessian 矩阵H(x,y)可以表示为
H(x,y)最大特征值所对应的特征向量即为光强法向(nx,ny)。 设像素点(x0,y0)的法线方向为(nx,ny),沿着法线方向对图像灰度进行二阶泰勒展开:

则光条中心线亚像素坐标为(x0+tnx,y0+tny)。
上述步骤虽可以较为准确地提取光条中心线, 但部分受工件表面瑕疵干扰严重的光条依然会导致提取中心线的部分坐标产生误差。 如图4 (a) 所示, 单幅结构光条纹能够提供的三维结构信息量有限, 拟合中心线无法对细微的异常值做补偿。 为降低这些误差点对三维重建精度的影响, 增强光条中心线的抗干扰能力, 引入一种基于差分多线结构光的中心线提取方法。
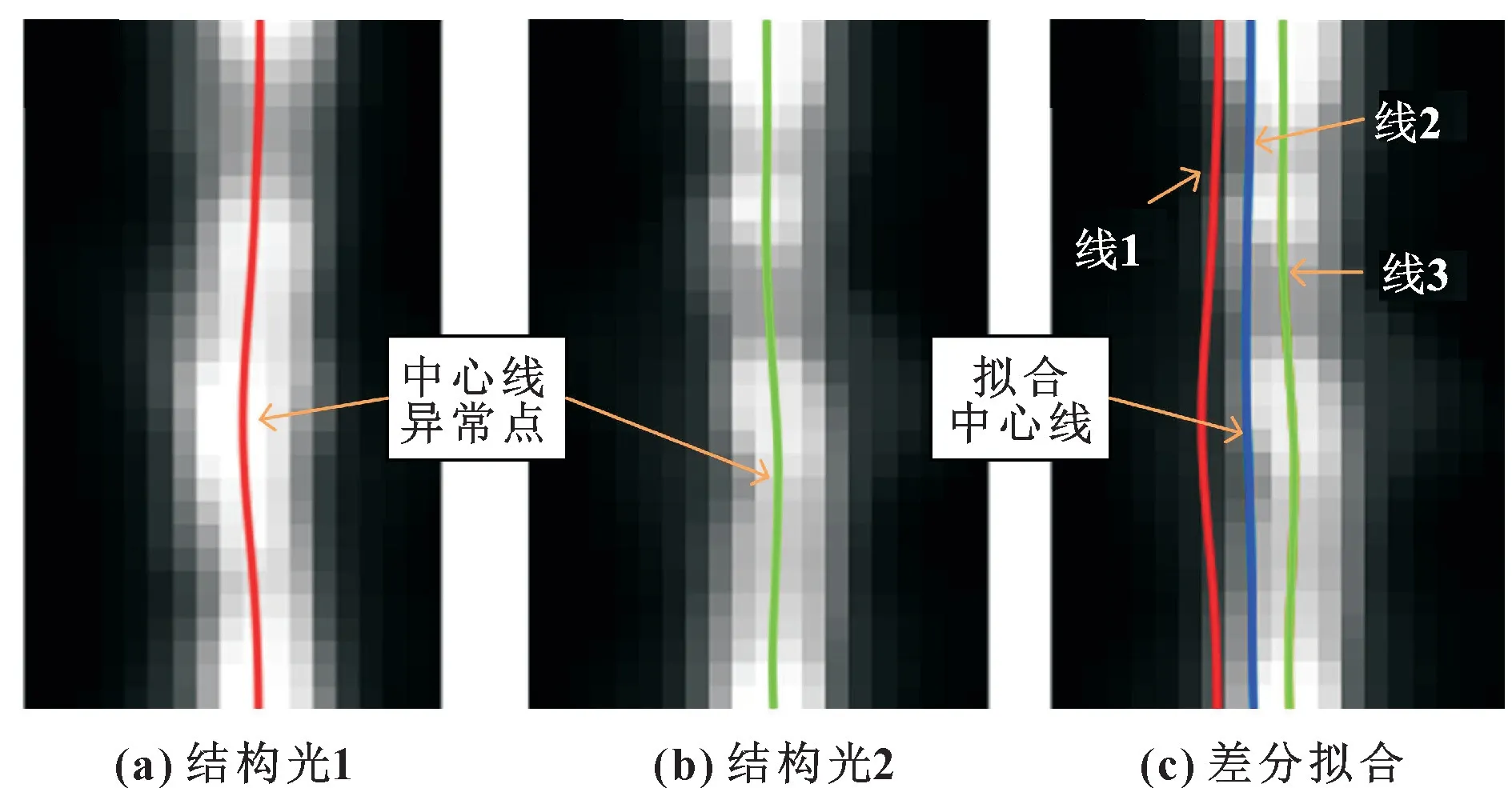
图4 Steger 法与差分法提取的中心线Fig.4 Centerline extracted by Steger method and differential method: (a) structured light 1; (b) structured light 2; (c) differential fitting
双目相机在采集一幅多线结构光图案后, DLP投影仪将投影图案整体水平移动一个像素, 并由双目相机再次采集。 以左相机为例, 对2 幅结构光图像分别提取每道光条的中心线, 如图4 (a) (b) 所示的2 道结构光图像即为同一光条图案在整体水平移动一个像素前后产生的不同效果, 将这2 道光条视为一组差分结构光。
对无编码的双目结构光系统, 特征点匹配的顺序需严格对应, 因此对左相机2 张照片中的中心线分别以左上角起始点纵坐标值递增排序, 将次序一致的中心线视为同一组差分结构光中心线, 使2 幅图像中每一组差分光条的中心线都可以相互对应。
对每组差分光条的2 条中心线, 取拥有相同行坐标的2 个点视为有效点, 再计算有效点列坐标的平均值, 即可拟合出该组差分结构光的新中心线。 新中心线坐标(xn,yn)的计算方法可以表示为
拟合效果如图4 (c) 线2 所示, 与单次投射结构光计算出的光条中心线相比, 新中心线在2 道差分结构光的相互补偿下, 更符合工件表面的实际轮廓,提高了提取平面特征点的稳定性。
对右相机采集的图像同样进行上述提取新中心线的步骤, 由于左右相机下各自拟合的新中心线的线序依然不变, 则再次依照线序, 以相同行坐标的原则,筛选出新中心线下可以相互匹配的坐标点, 并依照新中心线的线序和行坐标递增排序, 如图5 所示, 将左右图像中同一线序下同一行坐标的点视为立体匹配特征点, 由此遍历所有新中心线, 最终得到所需的特征点。
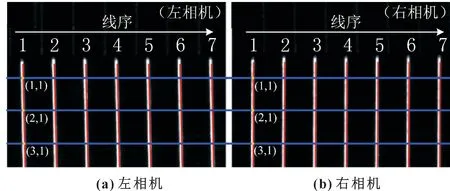
图5 新中心线线序及特征点匹配Fig.5 New centerline sequence and feature point matching:(a) left camera; (b) right camera
以线序和行坐标约束的排序方式避免了无编码双目结构光系统立体匹配失序的问题。 将匹配的特征点三维重建, 即可获得工件被测平面的点云。
2.2 基于Tukey 权重函数的平面拟合
三维空间中常见的平面拟合方式有RANSAC 拟合法[13]、 ICP 配准法[14]和最小二乘法。 最小二乘法因计算方式简单而得到了广泛的应用, 但是因其拟合过程中对点集内每一个点都赋予了相同的权重, 使拟合结果容易受到异常值干扰。 RANSAC 和ICP 配准法都是采用迭代方式估计预置数学模型的算法, 其不同之处在于ICP 配准法需要同时确立初始点集和目标点集, 是一个求取点集刚性变化的过程; 而RANSAC则是在点集中随机抽取用于估算预置模型的若干样本, 并迭代出样本内置信点最多的模型作为结果, 但是受阈值和迭代次数的影响, 容易产生局部最优解。
为提高拟合平面的稳定性, 减少工件平面点云受到如倒角、 破损缺陷等异常情况的干扰, 采用Tukey权重函数[15]对最小二乘法做出改进, 降低异常点的干扰。
设平面方程为z=ax+by+c, 构建误差函数为
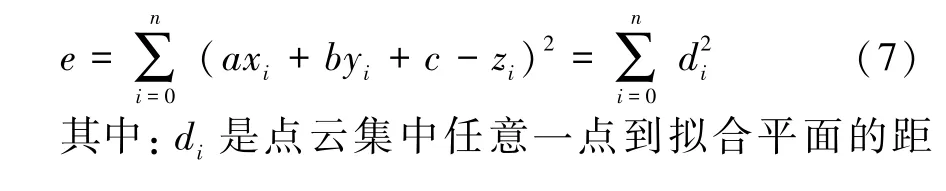
式中:τ为消除异常值的剪裁因子;δi是每个点到拟合平面的距离阈值。 将点集中异常点的距离阈值设置为σδ, 以下式表示:

经整理, 将求解自变量a、b、c的过程表示为矩阵形式:

2.3 基于Tukey 权重函数的边缘提取方法
为获取准确的工件边缘, 利用投影仪照亮工件的边缘部分, 改变工件表面与背景的对比度。 使用Sobel滤波器[16]增强边缘特征, 并通过膨胀腐蚀和筛选轮廓面积的方式排除大部分干扰点, 保留工件轮廓信息,提取出轮廓的粗边缘。 随后沿着工件边缘方向, 每隔若干像素绘制一个测量矩形, 测量矩形如图6 所示。
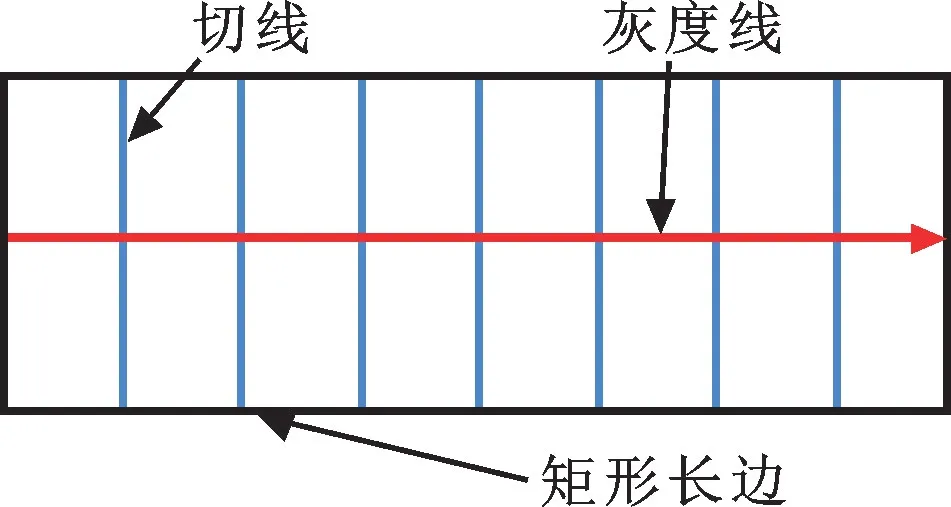
图6 测量矩形示意Fig.6 Schematic of measuring rectangle
矩形的长边与工件边缘近似垂直, 取测量矩形2条长边的中心线作为灰度线, 在矩形内部沿着灰度线每隔一个像素宽度做一条矩形切线, 并沿着灰度线方向计算每条切线的平均灰度值, 作为灰度线上的灰度分布函数, 其中, 切线上各点的灰度值采用双线性插值法计算[17]。
随后对灰度分布函数作高斯平滑, 并求一阶导数, 取导数极值点作为一个轮廓点, 提取边缘效果如图7 (a) 所示。 对同一边缘上的多个边缘点进行直线拟合, 即可作为工件的实际边缘轮廓线。
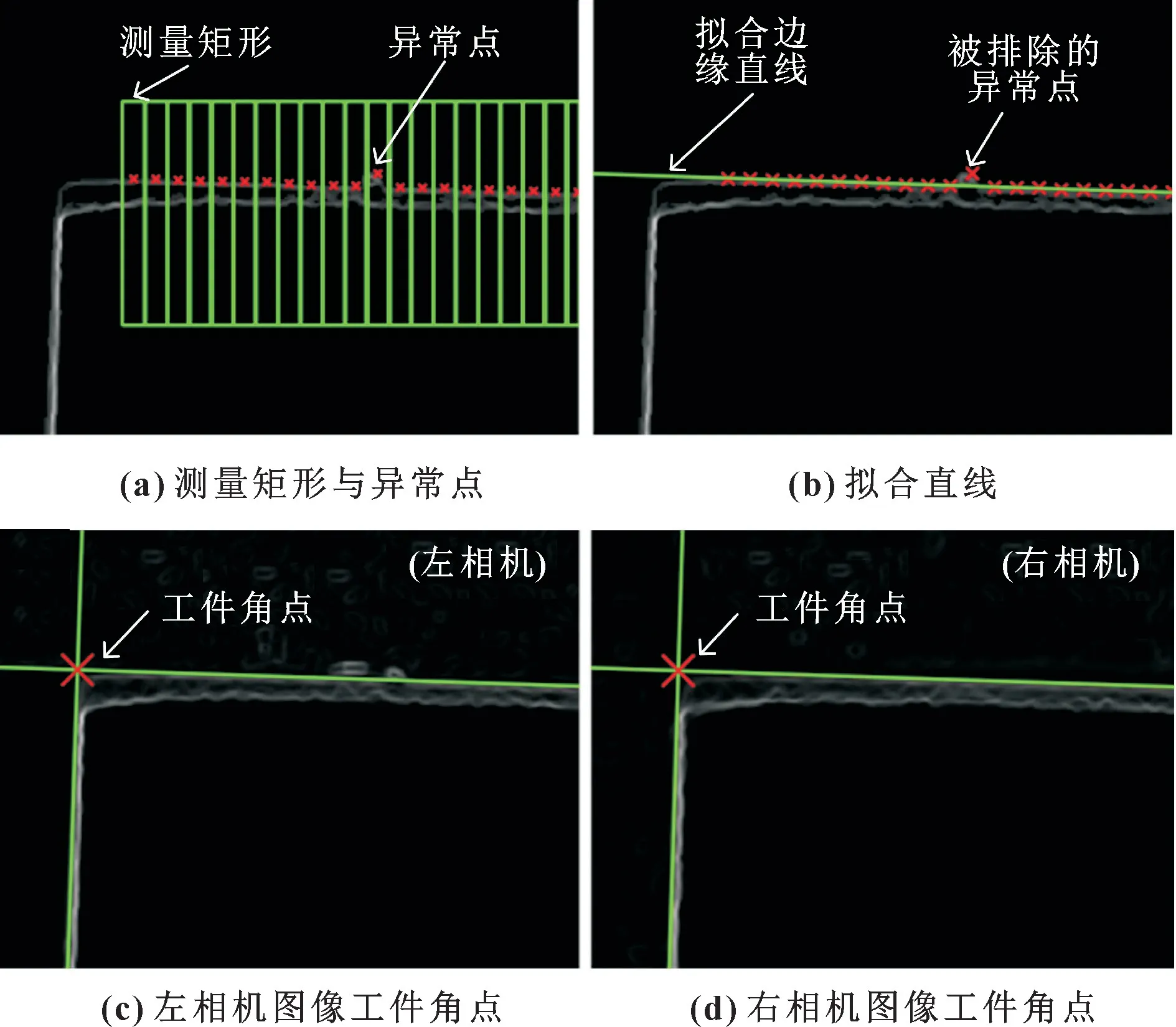
图7 提取工件边缘点示意Fig.7 Extracting workpiece edge points: (a) measuring rectangle and exception points; (b) fitted line;(c) workpiece corner in left camera image;(d) workpiece corner in right camera image
为避免提取异常的边缘点对拟合直线产生干扰,再次引入Tukey 权重函数对各点加权。 设直线方程y=ax+b, 构建误差函数:
式(13) 可由式(11) 递推, 拟合直线效果如图7 (b) 所示, 拟合的直线排除了异常点的干扰。由此拟合多条工件轮廓, 如图7 (c) (d) 所示, 各轮廓线的交点即为工件实际的角点。 将工件角点和若干边缘点的点云X、Y坐标映射至拟合平面, 即可求得工件边缘实际三维坐标, 获取工件三维位姿。
3 实验及结果
将实验设备和待测工件置于三坐标测量平台(蔡司CONTURA G3, 探头为VAST XXT, 分辨率0.002 mm), 实验平台如图8 所示。

图8 实验平台示意Fig.8 Experimental platform
3.1 平面精度验证实验
3.1.1 平面抬升精度验证
将待测工件置于三轴精密滑台上, 并由双目结构光系统采集工件被测初始平面的点云数据作为基准平面。 随后在滑台行程范围内, 每次沿着滑台Z轴方向对滑台抬升0.5 mm, 并由三坐标仪测量每次平面抬升的实际距离da作为真实值, 一共抬升10 次。 双目结构光系统依次采集滑台抬升后的平面图像, 提取平面点云数据, 计算每个点云到基准平面的相对距离di, 取其均值d-作为系统测量的平面抬升距离值。
分别对使用差分结构光和普通结构光的2 种方法进行试验, 将每次抬升滑台的测量结果d-与三坐标仪测量值da进行比较, 结果如图9 (a) 所示, 2 种测量方法的平均距离相对误差都没有超过±0.01 mm, 符合测量要求。 而使用差分结构光方法的距离标准差则明显小于对照组, 如图9 (b) 所示, 其最大标准差仅为0.023 mm, 提取平面点云的稳定性提高了16.67%~55.17%, 证明使用差分结构光的方法有效可靠。
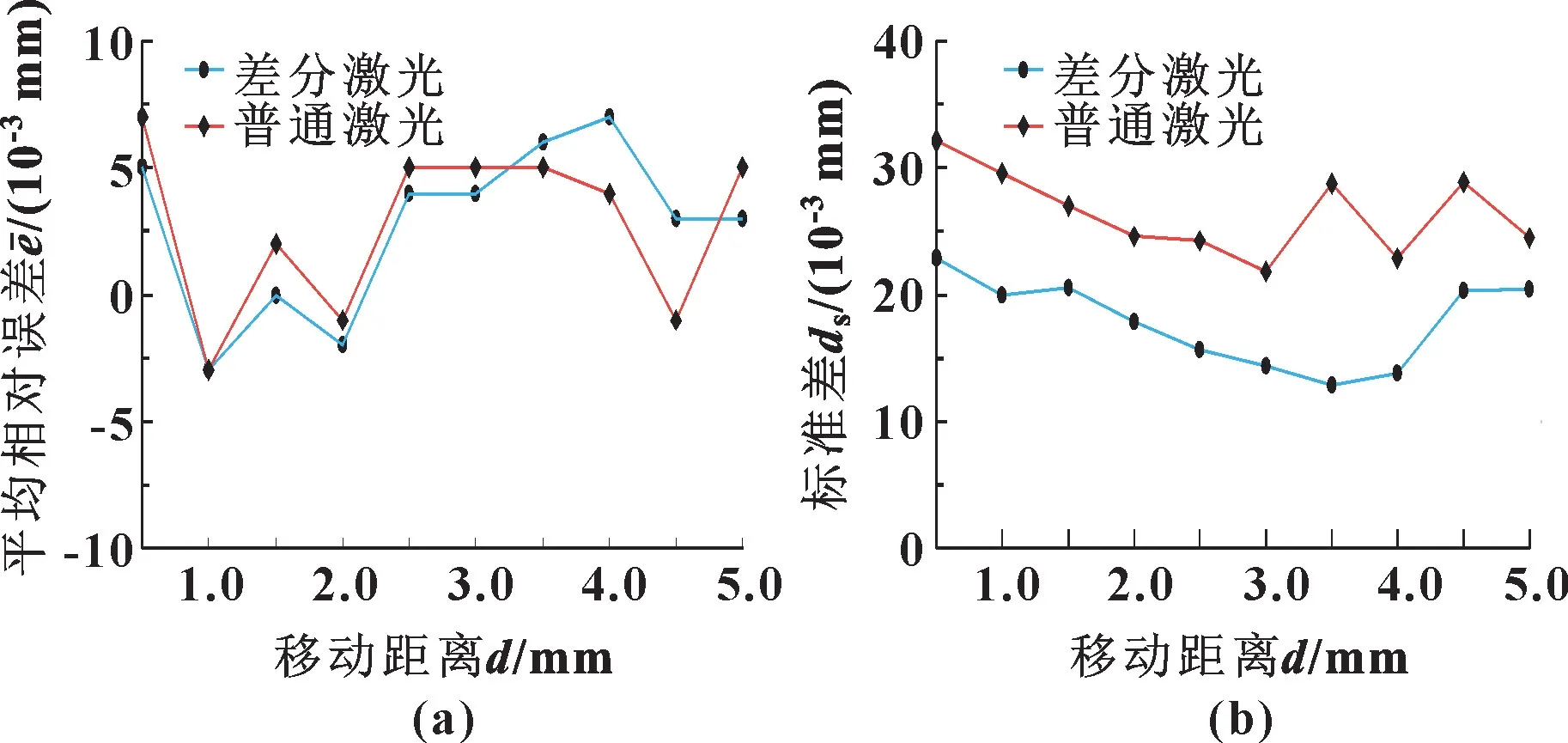
图9 测量平面点云至基准平面平均距离相对误差(a) 和标准差(b)Fig.9 Relative errors (a) and standard deviations (b) of the average distance from the point cloud to the reference plane
3.1.2 平面法向量稳定性验证
为测量Tukey 权重拟合平面的法向量稳定性,将工件静置于精密滑台上, 由投影仪分别沿同一水平方向移动多线结构光图案10 次, 每次平移一格像素, 使结构光图案可以完全扫描整个被测平面,且每平移一次图案拍摄5 组照片, 总计拍摄50 组照片。 分别利用最小二乘法、 RANSAC 拟合法和Tukey 权重法拟合50 次平面, 各自计算3 种拟合方法的法向量均值作为被测平面的实际法向量, 随后计算各拟合方法下每组平面法向量与实际法向量的夹角偏差。
由图10 与表1 可知: 使用Tukey 权重法拟合平面可以大幅降低异常数据对平面拟合质量的影响, 其均方根误差相较使用最小二乘法和RANSAC 拟合法的对照组分别减少了60.0%和19.6%, 法向量最大偏离误差仅为0.016°。

表1 不同平面拟合算法的法向量稳定性Tab.1 Normal vector stability of different plane fitting algorithms

图10 不同平面拟合算法的法向量偏差对比Fig.10 Comparison of normal vector deviations of different plane fitting algorithms
3.2 水平位移精度验证
在滑台行程范围内, 将滑台分别沿着x轴和y轴方向每次移动0.5 mm, 由三坐标仪测量每次滑动的距离作为实际值, 一共移动10 次。 相机检测工件的角点坐标, 并将角点映射到工件被测平面上, 分别计算映射角点在滑台沿x轴和y轴方向移动时的位移增量, 对比检测值与实际值的误差。 由图11 可知: 在多组实验验证下, 系统在x轴方向上的检测误差最大为0.024 mm, 在y轴方向上的检测误差最大为0.028 mm。 上述结果表明: 该方案用于检测工件边缘和提取角点也具有较高的精度。
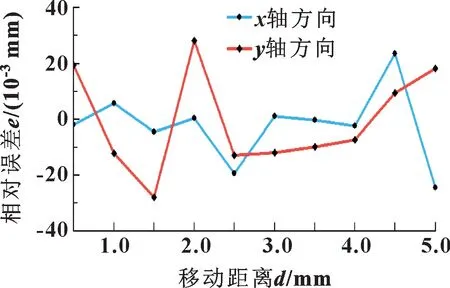
图11 x 轴与y 轴方向相对误差Fig.11 Relative errors of x-axis and y-axis direction
4 结论
针对一类带有平面特征但表面粗糙且纹理复杂的金属工件位姿检测问题, 设计了如下检测方法:
(1) 将复杂纹理工件的局部特征作为检测重点,采用投影差分多线结构光的方法, 提高了提取光条中心线的精度;
(2) 利用极线约束的特性, 设计了无编码双目结构光系统特征点匹配方法, 提高了提取平面特征点的稳定性;
(3) 基于Tukey 权重函数改进拟合算法, 提升了工件被测平面的拟合精度和提取工件边缘和角点的精度。
最后利用分辨率为0.002 mm 的蔡司三坐标仪和三轴精密滑台验证算法精度, 将检测结果与测量值做比较, 实现了提取粗糙平面点云标准差小于0.023 mm, 平均深度误差小于0.01 mm, 角点坐标在x轴方向最大误差为0.024 mm、 在y轴方向最大误差为0.028 mm, 法向量最大偏离误差仅为0.016°的结果,可以满足工件三维位姿检测的需求。
