基于概率路由的出租车共乘调度算法
2024-03-05蔡文广刘佳旭张小欣
蔡文广 刘佳旭 张小欣


收稿日期:2023-06-02;修回日期:2023-08-01 基金项目:辽宁省教育厅青年项目(LJ2019QL022)
作者简介:蔡文广(1998—),男,辽宁阜新人,硕士研究生,CCF会员,主要研究方向为时空数据管理、数据挖掘;刘佳旭(1979—),男(通信作者),辽宁葫芦岛人,讲师,硕导,博士,主要研究方向为时空数据管理、群体智能、城市计算、数据挖掘等(liujiaxu@buaa.edu.cn);张小欣(1998—),女,辽宁营口人,硕士研究生,主要研究方向为时空数据管理、数据挖掘.
摘 要:针对现有的拼车方案大多服务在线乘客请求,而忽略了离线乘客请求,导致出租车资源无法得到充分利用这一问题,提出了一种基于挖掘历史出行轨迹数据的概率路由拼车优化算法。该算法根据乘客请求的历史时空数据计算出区域概率转移矩阵,并使用该矩阵优化平台为出租车推荐拼车路径,提供了历史数据和拼车问题相融合的一种解决方案,可以有效提高出租车的载客量。在保障离线乘客接载率、在线乘客忍耐度的同时,使用松弛时间的度量指标,可以在O(n)内对整条路径的乘客忍耐时间进行评估预测,并用迪杰斯特拉算法对绕行区域进行路径规划,让出租车的绕行距离最短。使用滴滴GAIA真实数据集对算法有效性进行验证,结果显示,该算法在服务请求数量上高于基准算法12%。
关键词:共乘;路径规划;K-means聚类;概率路由
中图分类号:TP391.41 文獻标志码:A
文章编号:1001-3695(2024)02-017-0432-06
doi:10.19734/j.issn.1001-3695.2023.06.0248
Algorithm for taxi ride-sharing scheduling based on probabilistic routing
Cai Wenguang,Liu Jiaxu,Zhang Xiaoxin
(College of Software,Liaoning Technical University,Huludao Liaoning 125105,China)
Abstract:Aiming to address the issue that current ridesharing solutions mostly focus on serving online passenger requests and overlook offline ones,leading to underutilization of taxi resources,this paper proposed a probability-based routing ridesharing optimization algorithm that relied on mining historical travel trajectory data.This algorithm calculated a regional probability transition matrix from historical spatiotemporal data of passenger requests and utilized this matrix to optimize the recommended ridesharing routes for taxis.It presented a solution that integrated historical data with the ridesharing problem,effectively increasing the taxis passenger capacity.By ensuring the offline passenger acceptance rate and online passenger tolerance,the algorithm employed a relaxed-time metric to predict and evaluate the passenger tolerance time for the entire path in O(n) time,and used the Dijkstra algorithm to plan routes through detour areas,minimizing the detour distance for taxis.This paper validated the effectiveness of the algorithm by using the real-world DiDi GAIA dataset.Experimental results demonstrate that the proposed algorithm outperforms the baseline algorithm by 12% in terms of the number of service requests served.
Key words:ride-sharing;route planning;K-means clustering;probabilistic routing
0 引言
随着共享经济的快速发展,通过共享闲置社会运载资源,为消费者提供服务的拼车平台已对交通运输产生了深远的影响。为了提高出租车的空座利用率,降低乘客的出行成本,滴滴出行等平台[1,2]提供了共享拼车的服务。当出租车与多名乘客有相似的行程时,共乘平台允许两者共享一辆车,这样可以显著缓解城市交通拥堵,降低能源消耗,实现出租车和乘客的双赢。由于出租车在城市中的便利性和实用性[3],共乘成为一种高效的交通出行方式[4,5]。与基于私家车的拼车[6]不同,其乘车请求是静态的,可以提前规划拼车路线。出租车拼车更复杂,乘车请求和出租车都是高度动态的模式。更糟糕的是,有一些乘客不会明确提交他们的请求,而是在路边呼叫出租车,在城市中没有固定的路线运送乘客,这种拼车方式难度很大。出租车需减少路边乘客的等待时间,并及时服务乘车请求,同时还要更新出租车时间表和路线以保证服务质量,导致出租车实时调度极具挑战性。
目前,学者们已经提出了很多共乘问题的算法,成果主要集中在以下优化目标,例如从驾驶员的角度最小化总行程[7]或最大化共乘系统的服务率[8],从平台的角度最大化平台收益[9]等。共乘问题是NP-hard问题,需要设计近似算法为每辆出租车寻找合适的路线。Tong等人[10]优化了共乘算法的时间复杂度,利用动态规划的方法把一条路线上的各个事件点的时间戳在O(n)时间内预计出来。当出现一个新的请求,可以在O(1)时间内计算出最优的插入位置,时间复杂度从O(n3)降到了O(n)。Zheng等人[11]考虑拼车平台收益问题,用贪心策略把订单集和车辆集进行匹配,选择最优的匹配对,提出一种定价机制,更好地激励出租车和乘客参与拼车。Cheng等人[12]优化了平台收益目标,提出一种动态共乘框架,用机器学习模型预测每个区域未来的乘车需求,然后用排队论把新到来的车辆分配给需要的区域,并在调度过程中考虑平台的最大化整体收益以及对乘客满意度的影响。Li等人[13]考虑价格和社会关系对乘客的影响,提出一种新颖的定价方案,设计一种高效的剪枝算法,为乘客推荐前k个合适的出租车。Luo等人[14]考虑请求数量远大于出租车的数量,提出一种距离优先和贪心策略相融合的匹配方法,从而提高了平台整体服务率并实现了出租车最小绕行距离。Ma等人[15]正式定义了生成时间表的大规模实时出租车服务问题,提出单边出租车搜索、双边出租车搜索算法和過滤无效候选集的时空索引相融合的方法。Na等人[16]根据出租车和乘客具有相似的路径,提出一种高效的共享路径百分比框架,结合二分图的匹配筛选出权重最优的匹配结果。Chen等人[17]在动态拼车问题中考虑时间和价格的影响,乘客可以从时间的角度选择时间短的方案,乘客也可以从价格的角度选择价格低的方案,并使用大量剪枝技术筛选掉不符合条件的候选集。Ma等人[18]提出一个移动云框架的出租车共享系统,并根据时间、容量和价格为乘客分配合适的出租车。Huang等人[19]考虑实时大规模拼车问题,提出了分支界定算法和整数规划的方法,但是这两种方法的时间复杂度相对较高,为此又提出了动态树的算法,大大降低了时间复杂度。Lin等人[20]利用出行需求的数据来优化拼车路线,把它归结为一个满足乘客出行延时要求和在线作出事先不知道出行情况下的决策优化问题,提出一个两阶段动态规划的解决方案。Yuen等人[21]提出最短路径不是共享出行的最佳路径的问题,把搜索空间缩小到一个有向无环图中,用动态规划的方法来解决,并使匹配乘客的失败率降低40%,同时还将客户的等待时间缩短20%。Lowalekar等人[22]认为实时拼车平台的关键是应该把请求分成正确的组,使得系统的服务请求、收入和延时等目标可以被自然优化,通过设计一种区域路径的方法,用在线和离线组合的方法来优化请求组合,并从长远的角度出发,预测未来可能出现的乘车请求,在线生成更优的请求组合。Liu等人[23]把离线乘客和在线乘客都作为拼车的用户,从在线乘客的移动方向出发,能更好地为乘客寻找到更合适的车辆。共乘的众多优点,引起学术界和工业界极大的兴趣。
从上述研究中可以看出,现有的共乘问题主要研究在线乘客,而缺少对离线乘客的关注。根据一份出租车研究报告[24],离线乘客占据了总拼车人数的13.71%,并且有41.68%的人既喜欢离线拼车又喜欢在线拼车。为了最大化服务乘客数量,本文提出了一种基于挖掘历史轨迹数据的概率路由算法,通过出租车日常转移方式对道路网络的顶点进行聚类,得到的转移概率矩阵可以预测未来出现的离线乘客。因为路径规划是NP-hard问题,本文将出租车路线中的行程事件分区,减少整个道路网络的搜索空间,可以在多项式时间内求解。为了寻找离线乘客,基于历史订单数据挖掘乘客出行需求的潜在规律,用条件概率挖掘出一条累积出现离线乘客概率最大的路线。
1 问题定义
定义1 道路网络。道路网络是由图G=〈V,E〉的多个顶点和多条边组成的无向图,每条边(u,v)∈E,表示从顶点u到顶点v的旅行成本,旅行成本是在旅行中的时间或者距离,其中dis(u,v)是两个顶点之间最短的旅行成本。
定义2 请求。请求R分为在线请求和离线请求,在线请求R+=〈or,dr,tr,er,Kr,arr〉,or∈V是请求的起点,dr∈V是请求的终点,tr是请求的发布时间,er是请求的截止时间,Kr是请求中乘客的数量。离线乘车请求R-只有在共享出租车偶然遇到时才能获知,这里使用R-专门表示离线乘车请求。
定义3 出租车。出租车由t=〈loct,St,Rt〉表示,其中loct表示出租车t的当前位置,St和Rt分别是出租车t的行程事件表和共享出行的路线。
定义4 行程事件。一个出租车的行程事件表St=〈L0,L1,L2,…,Ln〉,它是由出租车的当前位置loct和所有请求起点or和目的地dr的序列组成,事件L0是出租车的当前位置,后面的每个事件对应于在某个位置乘客上车或下车的位置,但是对于同一个请求R来说,它的起点or必须出现在终点dr的前面。
定义5 出租车的路线。根据出租车的行程事件表St生成出租车路线Rt,其指St中任意两个连续事件的行驶路径。对于共享同一辆出租车的请求,应制定有效的行程事件表,以便沿着计划的拼车路线依次接送乘客。
定义6 分区。给定一个出租车和一个行程事件St,在St中任意两个连续事件之间的路线对应一个分区。初始时,如果St有n个事件,那么就形成了n个区。
定义7 地标。空间簇Cz的地标顶点LMz∈Cz,它是由簇Cz内顶点的距离属性和概率属性组成,选择Rank(D,P)最大值为地标顶点,具体确定地标顶点LMz的公式为
Rank(D,P)=α×LMz到Cz内所有顶点的距离之和累加Cz内所有边的和+(1-α)×LMz 到簇C 的概率和Cz 内顶点的数量(1)
其中:α是平衡距离和概率的系数,默认值为0.5。为了公平地测量这两个因素,并将它们保持在相同的范围内,归一化到[0,1]。
定义8 最大化服务请求。给定一组乘车请求,包括在线请求和离线请求,以及道路网络上的一组出租车。目标是共享出租车在原来行驶的路线基础上寻找离线请求,使得服务的乘车请求数量最大化,而总的绕行成本最小化,同时也要受到以下時空约束:容量约束,出租车载客人数任何时候都不得超过租车的容量;时间约束,在一条路线中想要接载一个离线请求,必须满足已在车上的请求,能在最后截止时间er之前送达。
2 框架
本文方法的主要架构如图1所示,从出租车状态、乘车请求信息和历史出租车数据以及路线图获取输入,动态安排共享出租车服务在线和离线乘车请求。在出租车方面,它会不断上传自己的状态(包括位置、可用座位等)并从服务器接收和更新自己的路线;在请求方面,乘客可以向服务器提交乘车请求,或者以离线方式在路边呼叫共享出租车;通过挖掘历史出租车数据,筛选出隐藏在道路网络顶点中的热门上车位置,对这些顶点中暗含的转移方式进行空间聚类。通过聚类算法、行程事件分区和概率路由算法寻找离线乘客,如果寻找到合适的路线则返回更新的路线,否则返回原有路线。
2.1 阶段1 节点聚类
节点聚类的目的是为了预测离线乘客,让出租车有机会遇到离线请求。节点聚类需要从大量的历史出租车信息中挖掘出相似的转移方式。具体的地图分割过程如下:
a)地理聚类。首先利用K-means算法根据道路网络中顶点的地理位置将其分成k个空间簇。初始化阶段将所有顶点进行聚类,空间簇中的顶点在地理上是接近的。在后面的过程中,按比例对在步骤c)中导出的每个转移簇进行聚类。给出大小为n的转移簇,其顶点被分组到nkN+12」空间簇内,其中N是V中的顶点总数。
b)转移概率的计算。基于步骤a)中获得的k个空间簇,计算每个顶点vi的转移概率。每一项Bi,j(i=1,2,…,N和j=1,2,…,K)是在顶点vi到第j个空间簇内的转移概率,这可以利用历史出租车数据来计算。
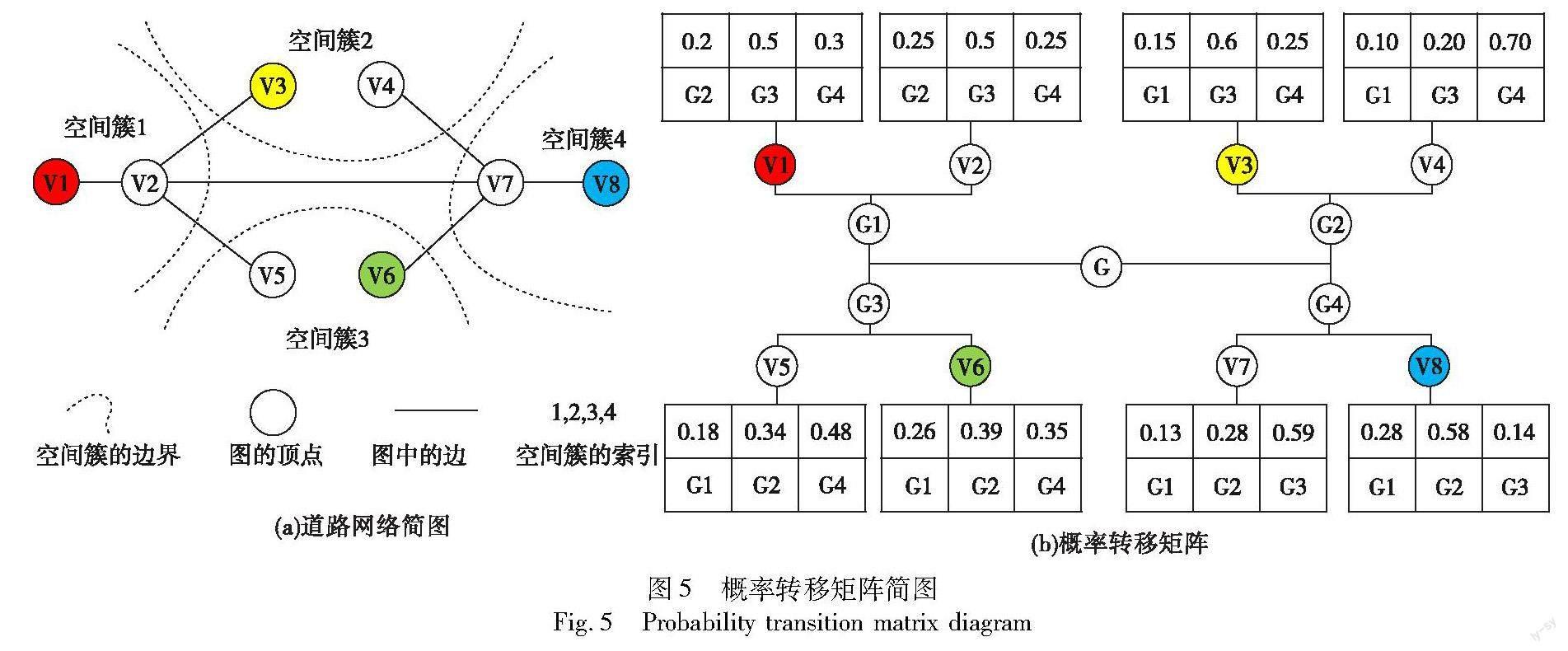
c)转移聚类。把矢量Bi看作顶点vi的移动特征,并使用K-means聚类算法根据所有顶点的转移概率矢量,将所有顶点分组为kt个转移簇,其中kt 2.2 阶段2 路线分区 路线分区是为了重新规划路径以遇到离线乘客,基于路线分区的关键是可以对行程事件进行分区并划分为n(行程事件的数量)个不相交的集合,并且独立地处理它们的目标函数OBJ(St)。路线分区基于绕道的概念,绕道表示插入新位置后与原始路径的行程时间相比增加的行程时间。当引入松弛时间,出租车在从一个事件行驶到另一个事件的区间中,对路线进行重新规划,让出租车更有机会遇到离线乘客,使服务请求数量达到最大化。当给定一条行程路线时,可以将其划分为n个分区,如图3所示。 分区1是出租车当前位置到事件L1的行驶区间,分区2是事件L1到事件L2的行驶区间。结合图3和松弛时间式(2)可以计算出每个事件的松弛时间,在所有事件的松弛时间集合中选择最小的松弛时间来约束下一阶段检查截止时间的约束:将slk[i]定义为在事件Li之后满足截止时间约束的绕行的最大忍耐时间(松弛时间),有 slk[i]=min{slk[i+1],ddl[i+1]-arr[i+1]}(2) 其中:arr[i]表示出租车到达事件Li的时间;ddl[i]表示在不违反最后截止时间约束的情况下出租车到达Li的最晚时间。具体而言,ddl[i]可计算为 ddl[i]=er-dis(or,dr)如果Li是起点 er如果Li是终点(3) 将arr[i]表示为出租车到达Li的时间,有 arr[i]=arr[i-1]+dis(Li-1,Li)(4) 计算完每个事件的松弛时间,选择最小的松弛时间规划搜索离线乘客范围的概率路由算法,虽然出现离线乘客的顶点非常多,但是不能无限制地去遍历,这是非常耗时的。把最小的松弛时间分配到具有最高概率遇到离线乘客的分区Pmax中,Pmax是由当前事件顶点到下一事件顶点簇的转移概率值决定的。当松弛时间小于阈值,直接结束循环(据图4最长边长在0~500 m的概率占绝大部分,出租车在街区中绕行500 m大约需要1 min,没有必要松弛,所以阈值选择1 min)返回原有的路线。目标是要选择最大的: OBJ(Rt)=max{分区i 的概率|i∈(1,n)}(5) 2.3 阶段3 寻找离线乘客 本阶段假设在不同时间、不同路段之间的离线请求是可以预测的,路线规划通常又是出租车调度的效率瓶颈。为了设计出满足以上两阶段要求的路径规划算法,提出了基于历史数据的预测结果进行分区过滤的Dijkstra最短路径算法,以优化概率路由算法。给定一个行程事件表St,通过阶段2得到的分区,对事件(Lz,Lz+1)∈St重新规划路线,即减少路线的搜索空间并返回一条在松弛时间约束内的可行路径。假设出租车在事件(Lz,Lz+1)∈St可能路线被表示为Rt=(Lz,LM1,LM2,…,LMn,Lz+1),其中Lz是分区z+1的起点,Lz+1是分区z+1的终点,从事件Lz到Lz+1经历了n个簇,其中LMi分别是簇i的地标顶点。 为了在路线分区阶段寻找到适合本次行程的路线,本阶段基于分区过滤和转移概率矩阵的概率路由算法组成,它支持出租车有机会遇到合适的离线乘客。如果R-是在松弛时间内找到乘客,并且满足时空约束,则认为该请求R-被认为是合适的。从理论上讲,应该在可行的松弛时间内计算所有分区的所有顶点上合适请求的概率,并计算一条累积最大概率的路线来搭载离线乘客。然而这在计算上是十分复杂的,已经被证明是NP完全问题[16],假设离线乘客的出行需求遵循时间相关的统计模式。在时间戳t和事件Lz处,存在概率P(Lz|t)的行驶要求,共享服务以条件概率P(Lz+1,Lz|t)到达节点z+1。进一步假设乘客到达在不同节点和不同时间戳是独立的。因此,该路线的概率可以计算为 P(Rt)∑P(Lz+1,Lz|t)(6) s.t.→t≤min{slack[1],…,slack[n]}+dis(Lz,Lz+1)(7) 图5(a)描述了道网聚类后空间特征的一个示例,共分为四个簇,v1、v3、v6和v8分别是空间簇1、空间簇2、空间簇3和空间簇4的地标顶点,每个簇都包含两个顶点,虚线代表空间簇与空间簇的边界。图5(b)描述了图5(a)中各个顶点在历史出租车数据中的转移概率,其中每个子簇Gu包含一个顶点子集Vu和一个边集Eu,每个顶点集又包含一组map集合。例如在子图G1中有两个顶点v1和v2,v1中的key就是其他簇的索引,value是v1到其他各簇的转移概率,并且使得∑k-1j=1Pij=1,Pij是顶点vi到簇j的转移概率。为了避免大量的计算,在多个分区中只选择一个分区,在这个分区规划出一条高概率遇到离线乘客的路径,主要步骤如下: a)概率路由过程。给定一条出租车路线,根据阶段2得到的分区,选择用迪杰斯特拉算法遍历从源行程事件到目标行程事件由地标顶点映射的簇,在这些簇集内再次枚举从源行程事件到目标行程事件的累积转移概率和最大路径。同时满足已经在出租车上乘客的最后截至日期的约束,它是行程事件(Lz,Lz+1)之间具有最大概率遇到合适离线乘客的路线。如果在此过程中找不到有效的路线,则将返回出租车上原有的路线St。由于概率路由比普通路由的计算时间要长,出租车仅在有足够的空闲容量且松弛时间充足时才调用它,否则返回原有路线。尽管在规划中遇到离线乘客的路线可能会带来轻微的延迟,但它可能会为出租车和离线乘客带来各自的收益。 如算法1,第1行为初始化出租车路线分区的集合、松弛时间集合和尝试遍历寻找离线乘客的次数。第3~10行表示如果出租车的容量小于0,直接退出循环,否则對出租车的行程路线进行分区,根据式(2)计算每个事件的松弛时间,在松弛时间内选择出现离线乘客概率最大的分区。第11~19行表示在选出的分区重新对出租车路线进行规划,利用地标顶点筛选出要遍历的簇,过滤掉不符合条件的簇,再利用每个簇内顶点的转移概率值,规划一条累积最大概率权重的路径,其中最短路径需要用迪杰斯特拉来寻找。如果找到有效路线,则将返回更新的路线USt,重复这两个步骤,如果找不到有效路线或超过了尝试的次数,则返回原有的路线St。 算法1 PR-share算法 输入:A taxi with route St。 输出:A taxi with updated route USt。 1initialize P=、slack[]、attempt=0 2while(true){ 3 if remaining capacity of taxi < 0 4 break; 5 else{ 6 for Li∈St do { 7 Construction partition P=P∪Pi∈(Li,Li+1) 8 Calculate slack[i] According to formula 2 9 } 10 Select P* = max OBJ(Rt) 11 while(true){ 12 Select the maximum weighted path Rt from Lz to Lz+1 with Landmarks in clusters 13 Find the shortest path Rt using the Dijkstra algorithm on USt 14 attempt=attempt+1 15 if Rt is valid 16 return USt 17 if attempt>5 18 return St 19 } 20 } 21} b)时间复杂度。为了服务请求,需要检查出租车中的所有行程事件,然后选择合理绕行成本的路线,概率路由的算法时间复杂度为O(mNDP/K),其中m是行程事件的个数,N/K是平均每个簇中顶点的个数,D是查询转移概率矩阵的次数,P是所选择簇的数量。因为任何两个顶点之间的最短路径可以预先计算和缓存,所以最短路径查询与以前的研究一样可以在O(1)时间计算出。 3 实验分析 3.1 实验数据 本文使用滴滴GAIA计划公开发布的真实世界数据集[25]进行实验评估,该数据集包含成都市2016年11月18日上午10:00~11:00的数据。实验中的时间段是非上下班高峰期,大多数出租车的在线乘车请求不足,有足够的空余容量,可以启用概率路由算法。数据集中每个元组都由上车的经度/纬度、下车的经度/纬度和发布时间组成29 534个出租车请求。使用开源的OpenStreetMap[26]导出成都市的道路网络,并将道路网络表示为一个由214 440个顶点和466 330条边组成的无向图G(V,E)。表1总结了请求的数量以及导论网络中顶点和边的数量。 3.2 实验方法 为了模拟一个典型的共享出行应用程序,应遵循已有工作实验[27]中的设置,采用相同的请求集、顶点集和边集,改变实验的参数,例如,使用2k、5k等不同数量的出租车和其他的默认参数进行评估。转移概率是通过某一个顶点附近的若干个历史订单数量来近似计算这一顶点的转移概率,当历史订单规模越大,预测得会更准确,本文将每个请求的起点和终点预先映射到道路网络中最近的顶点。出租车的初始位置是从道路网络顶点中随机选择的,当它服务请求时,会按照计划的路线行驶到目的地。为了模拟离线乘车请求,随机将5 000个在线请求的起点、目的地和发布时间对出租车不可见,测试出租车能否完成离线请求的任务。本文采用服务请求的数量和响应时间指标来评估算法的性能,表2列举了实验的主要参数,默认参数值以粗体标记,例如:发布时间为tr的请求的默认截止时间为tr+10 min。所有实验均在Intel Core i7(2.80 GHz)和16 GB RAM的服务器上进行,所有算法均在Ubuntu环境下使用 C++来实现。在相同的实验设置下,用Python生成10次不同位置的出租车初始数据,并报告同一设置下的平均结果。 3.3 实验结果与分析 将本文方法与No-Sharing、T-Share[15]、mT-Share[23]、NDP[7]进行比较。No-Sharing是用一对一的方式来服务乘客,将乘车请求分配给搜索范围γ内最近的空出租车。T-Share 是最先进的方法之一,使用空间网格对所有出租车和请求进行索引跟踪,从请求起点和请求终点的γ范围内双边搜索候选出租车,如果找到有效的候选者,它将立即返回。mT-Share首先在请求的搜索范围γ内选择候选出租车列表,在出租车列表的基础上又用出租车向量和请求向量的夹角余弦值判断是否服务新请求,向量的起点是出租车(请求)的起点,向量的终点是出租车(请求)的终点。NDP把出租车和请求的匹配问题转换为请求的插入问题,在满足最小化绕行成本的前提下,结合動态规划和最大流算法,在一个分区框架中让新请求选择最适合的插入位置。 图6为改变出租车数量的影响结果。所有算法的服务数量随着出租车数量的增加而增加,在服务数量方面,PR-Share优于T-Share和No-Sharing,因为它优化了拼车路线,可以返回更多的请求-出租车匹配对,与mT-Share和NDP相比,PR-Share略差一些。例如,在3 000辆出租车的情况下,所服务的No-Sharing、T-Share、NDP、mT-Share和PR-Share请求数量分别为6 521、7 841、10 032、10 619和8 934。与 T-Share和No-Sharing算法相比,PR-Share分别多提供了12%和27%的乘车请求,这是由于概率路由可以服务更多的离线乘客,而其他算法忽略了这一点。 通过改变簇数κ并保持其他参数为默认值来进行实验,图7为T-Share、mT-Share、NDP和PR-Share对服务请求数量的影响。T-Share、mT-Share和NDP通过改变网格的大小可以近似地和PR-Share中簇的大小在功能上实现相同的作用,起初增加网格和簇的数量可以让服务请求的数量增加,然而随着增加数量的变多,服务请求的数量也开始减少。例如,κ=150,这是因为太小或过大的κ将导致增加和减少候选簇的集合,进而影响算法的性能。以PR-Share为例,当κ从100变化到150时,服务请求的数量增加了6%,服务请求的数量从6 123增加到6 547,然而当簇数增多,总的服务请求也慢慢变少。 图8为改变截止时间的结果,通过改变截止时间,出租车的搜索范围也会变化,随着截止时间的增大,算法的服务数量都有所增加。原因在于较长的截止时间允许搜索更多的请求,但是较长的截止时间会影响乘客的满意度。虽然增加了服务请求的数量,但是牺牲了乘客的忍耐性,等待时间变长导致增长速度缓慢。在截止时间为10 min,PR-Share比T-Share算法提高了14%。 图9显示响应时间随着可用出租车的数量增加而增加。很明显,No-Sharing总是可以在1 ms内处理请求,因为它只服务一个请求。PR-Share比mT-Share和T-Share需要更长的时间来响应请求,而NDP是最慢的一个。这是因为在决策阶段,NDP计算每个候选出租车的绕行下界是非常耗时的,一般来说,本文算法在100~280 ms就可以响应乘车请求,并且在响应时间上优于NDP 3~9倍。 图10显示在2 000辆出租车、150个簇集、容量为4和截止时间10 min情况下服务请求数量的结果,被服务请求的总数量由在线请求的数量和离线请求的数量组成。虽然PR-Share服务请求的总体数量没有NDP和mT-Share多,但是在离线请求数量上分别比mT-Share、NDP和T-Share多17%、29%和33%。 4 结束语 为解决现有共乘方案仅对在线乘客服务而缺少对离线乘客服务的局限性,针对现有求解离线乘客的方法并不能很好地与预测方法相匹配的问题,本文提出了一种挖掘历史出租车数据的概率路由算法。a)利用顶点附近的历史订单数据中潜在转移方式聚类,生成的概率转移矩阵预测离线请求;b)对出租车路线中的行程事件进行分区,选择出现离线乘客概率最高的分区,用概率转移矩阵在该分区重新规划路线。同时使用松弛时间,缩小寻找离线乘客的范围,提高了算法的灵活适应能力。通过在真实数据集上进行比较,验证了该方法不仅能有效地匹配离线乘客、增加服务请求的数量,还能进一步提高平台和出租车的收益。但是实验中的个别离线乘客很难被服务,未来将侧重于对这些离线请求的位置进行算法优化。 參考文献: [1]Didichuxing[EB/OL].https://www.didiglobal.com/. [2]Uberpool[EB/OL].https://www.uber.com/. [3]徐毅,童咏昕,李未.大规模拼车算法研究进展[J].计算机研究与发展,2020,57(1):32-52.(Xu Yi,Tong Yongxin,Li Wei.Research progress on large-scale carpooling algorithms[J].Journal of Computer Research and Development,2020,57(1):32-52.) [4]Zhang Shanfeng,Ma Qiang,Zhang Yanyong.QA-Share:towards efficient QoS-aware dispatching approach for urban taxi-sharing[C]//Proc of the 12th Annual IEEE International Conference on Sensing,Communication,and Networking.Piscataway,NJ:IEEE Press,2015:533-541. [5]Zhang Wei,Shemshadi A,Sheng Quan.A user-oriented taxi ride-sharing system with large-scale urban GPS sensor data[J].IEEE Trans on Big Data,2021,7(2):327-340. [6]He Wen,Wang Kai,Li Deyi.Intelligent carpool routing for urban ridesharing by mining GPS trajectories[J].IEEE Trans on Intelligent Transportation Systems,2014,15(5):2286-2296. [7]Xu Yi,Tong Yongxin,Shi Yexuan.An efficient insertion operator in dynamic ride-sharing services[J].IEEE Trans on Knowledge and Data Engineering,2022,34(8):3583-3596. [8]Lyu Jingwei,Hao Jiannan,Yao Shuzhen.A two-sided stable matching method in ridesharing[C]//Proc of the 8th IEEE International Conference on Cloud Computing and Intelligent Systems.Piscataway,NJ:IEEE Press,2022:671-675. [9]Elmer R,Gerard R C,Francis E.A game theory-based pricing technique for ridesharing pairings[C]//Proc of the 1st International Conference on Advanced Innovations in Smart Cities.Piscataway,NJ:IEEE Press,2023:1-5. [10]Tong Yongxin,Zeng Yuxiang,Zhou Zimu.A unified approach to route planning for shared mobility[J].Proceedings of the VLDB Endowment,2018,11(11):1633-1646. [11]Zheng Libin,Chen Lei,Ye Jieping.Order dispatch in price-aware ride-sharing[J].Proceedings of the VLDB Endowment,2018,11(8):853-865. [12]Cheng Peng,Jin Jiabao,Chen Lei.A queueing theoretic framework for vehicle dispatching in dynamic car-hailing[C]//Proc of the 35th IEEE International Conference on Data Engineering.Piscataway,NJ:IEEE Press,2019:2177-2189. [13]Li Yafei,Wan Ji,Chen Rui.Top-k vehicle matching in social ride-sharing:a price-aware approach[J].IEEE Trans on Knowledge and Data Engineering,2019,33(3):1251-1263. [14]Luo Hui,Bao Zhifeng,Choudhury M.Dynamic ride-sharing in peak travel periods[J].IEEE Trans on Knowledge and Data Enginee-ring,2021,33(7):2888-2902. [15]Ma Shuo,Zheng Yu,Wolfson O.T-Share:a large-scale dynamic taxi ride-sharing service[C]//Proc of IEEE International Conference on Data Engineering.Piscataway,NJ:IEEE Press,2013:410-421. [16]Na Ta,Li Guoliang,Zhao Tianyu.An efficient ride-sharing framework for maximizing shared route[J].IEEE Trans on Knowledge & Data Engineering,2018,30(2):219-233. [17]Chen Lu,Zhong Qilu,Xiao Xiaokui.Price-and-time-aware dynamic ride-sharing[C]//Proc of the 34th IEEE International Conference on Data Engineering.Piscataway,NJ:IEEE Press,2018:1061-1072. [18]Ma Shuo,Zheng Yu,Wolfson O.Real-Time city-scale taxi ride-sharing[J].IEEE Trans on Knowledge & Data Engineering,2015,27(7):1782-1795. [19]Huang Yan,Jin Ruoming,Bastani F.Large scale real-time ride-sharing with service guarantee on road networks[J].Proceedings of the VLDB Endowment,2013,7(14):2017-2028. [20]Lin Qiulin,Lei Deng,Sun Jingzhou.Optimal demand aware ride-sharing routing[C]//Proc of IEEE INFOCOM -IEEE Conference on Computer Communications.Piscataway,NJ:IEEE Press,2018:2699-2707. [21]Yuen C,Singh A,Goyal S.Beyond shortest paths:route recommendations for ride-sharing[C]//Proc of World Wide Web Conference.New York:ACM Press,2019:2258-2269. [22]Lowalekar M,Varakantham P,Jaillet P.Zone path construction based approaches for effective real-time ride-sharing[J].Journal of Artificial Intelligence Research,2021,70:119-167. [23]Liu Zhidan,Gong Zengyang,Li Jiangzhou.mT-Share:a mobility aware dynamic taxi ride-sharing system[J].IEEE Internet of Things Journal,2022,9(1):182-198. [24]Taxi research report[EB/OL].http://www.transformcn.com/Topics/. [25]Gaia[EB/OL].https://outreach.didichuxing.com/research/opendata/. [26]OpenStreetMap[EB/OL].http://www.openstreetmap.org/. [27]Asghari M,Deng Dingxiong,Shahabi C.Price-aware real-time ride-sharing at scale:an auction-based approach[C]//Proc of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.New York:ACM Press,2016:1-10.
