基于傅里叶成像网络的全息粒子成像技术研究

李宇杰, 程伟哲, 余 乐, 王华英, 王 丹, 李学燕,李伯仕

1. 河北工程大学数理科学与工程学院, 河北 邯郸 056038; 2. 北京理工大学深圳研究院, 广东 深圳 518057

粒子场主要由各种微小的物体构成,如细胞、环境中的微颗粒等,在医学和环保领域有重要应用。近年来,越来越多的人将三维成像用来检测粒子的形态、运动状态、空间位置等。例如,根据红细胞的数量来判断患者的健康状况,进而在临床医学假设病理过程,红细胞浓度可作为判断分子生物学化学用量的指标[1]。另外,燃烧后产生的颗粒物可以判断不同燃料的燃烧效率,颗粒越小表明燃烧得越充分[2]。在许多产业使用光散射分析颗粒大小用来把控产品的质量,例如制药业、美容化妆品行业、聚合物生产和食品业等[3]。数字全息术通过物光波和参考光波的干涉生成一张包含物体三维信息的全息图,且只需要一张全息图就可以重建物体的三维信息的特点,使数字全息术成为热门的三维成像方法。而数字全息关键点就是重建,传统全息重建算法对噪声敏感且计算复杂度高使得它们在实时或大规模应用方面表现不佳。随着深度学习的出现,发现可以有效解决传统算法遇到的问题,且各种网络架构已经证明可以有效处理图片方面的任务,例如卷积神经网络(CNN)[4]、循环神经网络(RNN)[5]以及生成对抗网络(GAN)[6],其出色的拟合能力,有效地解决线性或非线性映射任务。而且深度学习在数字全息方面已经有很多应用,例如,Rivenson等[7]使用CNN对全息图重建和相位恢复,同时对双像和空间伪影有很好的抑制效果。通过Y-Net网络可以大幅缩短全息重建时间[8]。O’Connor等[9]提出一种多尺度卷积网络有效去除全息重构过程中的负一级像与零级像。传统数字全息粒子场恢复方法需要通过图像处理以及各种算法才能获得粒子三维坐标、半径。而深度学习通过其强大的特征提取能力,可以有效地根据特定参数来表征颗粒,只需通过全息图就可以获取粒子的信息,不需要额外图像处理,进而加快数据处理效率。2021年,Shimobaba等[10]使用U-net网络对全息颗粒表征,并在三维粒子场中重建颗粒坐标和半径,实现了比理论值更高的定位准确性。此外,在2021年,吴羽峰等使用Dense_U_net网络对全息颗粒表征,有效提取粒子坐标、半径以及深度信息[11],虽然实现了很好的定位,但在重建质量上以及在大密度粒子群提取粒子时仍有不足,并且真实的粒子群往往是以大数量高密度出现。鉴于此,本文基于傅里叶成像网络(Fourier imager network,FIN)[12],提出一种融合注意力机制的傅里叶成像网络(squeeze and excitation Fourier imager network,seFIN)用来对全息粒子场定位。在CNN网络中卷积层的感受野大小的限制,对于一些尺寸较大的全息图会导致重建精度不足。而傅里叶成像网络利用经过训练的空间傅里叶变换(spatial Fourier transform,SPAF)模块[13]替代CNN网络中的卷积操作来处理全局空间频率信息。而加入的通道注意力机制(squeeze and excitation,se)模块可以实现不同通道间权重分配不同的优先级,抑制作用不大的通道,提高网络对图像细节的提取,从而实现高精度的颗粒表征。首先使用模拟生成三维粒子全息图,并将其作为网络的输入数据,使用表征法对全息图表征,作为网络的真实值。同时我们对seFIN网络的输出结果与Dense_U_net网络的结果质量进行比较,使用结构相似性(structural similarity index,SSIM)和峰值信噪比(peak signal to noise ratio,PSNR)作为网络输出图像的质量评判。最后,通过实验采集同轴全息图验证了傅里叶网络的可行性和有效性。

1 基础理论

1.1 层结构角谱法

数字全息经过物光和参考光干涉,生成包含物体振幅和相位信息的图像,投射到CMOS传感器在计算机上生成相应的全息图。记录过程表示为

(1)

(2)

λ为波长,k为波失,z表示物体到传感器距离。

在数字全息中,使用角谱法来进行数值重建。在角谱法中,全息图在频域内进行傅里叶变换和逆傅里叶变换,以还原物体的三维信息,包括振幅和相位:

E(x,y,z)=F-1{F{Iz(x,y)}×G(fx,fy;z)}

(3)

其中F和F-1为傅里叶变换及其逆变换,fx和fy表示频域坐标,z表示传播距离,G为传递函数:

(4)

同样地,基于角谱法的思想,我们将光场信息根据其深度距离z进行分层划分。每一层都代表了光场在不同深度的信息。这种分层方法允许我们分别处理每个深度层的光场信息,形成了一种适用于层次性光场处理的角谱法的变体[14]。

EHi(x,y,z)=F-1{F{Izi(x,y)}×G(fx,fy;zi)}

(5)

(6)

其中EHi(x,y,z)为每一层全息图的复振幅,zi表示每一层全息图的传播距离,通过累加所有层后可以获得一个完整的全息粒子场。

1.2 粒子场模拟生成及表征

在通常情况下,空气中的微粒子表现出布朗运动,这是由于它们不断受到气体分子的碰撞和热运动的影响。在不考虑重力或磁场等额外力的情况下,这些微粒子的运动是随机的、无规律的,它们在空气中无法被精确预测。为了体现粒子运动的无规律性,本文通过图1所示生成边长为5.12 mm的立方体区域在其中随机生成1～300个粒子,粒子大小在5～10 μm之间,每个粒子随机分布在距离传感器1～2.048 mm之间。然后通过将三维粒子场分层,并对每层粒子通过层结构角谱法得到子全息图,将子全息图在干涉面叠加,生成包含整个粒子场的全息图。最后根据模拟粒子场得到对应的粒子表征图,粒子表征使用(x,y,z,R)的形式来描述,(x,y)表示粒子的质心位置,(z)表示粒子纵深,(R)表示粒子的直径,通过粒子表征方法,将每个粒子的(x,y,z,R)坐标编码成一个512×512px的灰度图像。为了描述粒子特征,采用二维矩形而非二维圆形主要考虑到操作上的便利性。矩形在图像处理中易于检测和识别,同时测量其尺寸和计算灰度平均值的过程也更加直接和简单。使用矩形中心坐标表示粒子中心的位置(x,y)。用矩形边长代替粒子半径(R),矩形的灰度值作为粒子在z轴的纵深。其中灰度值与粒子深度位置(z)关系:

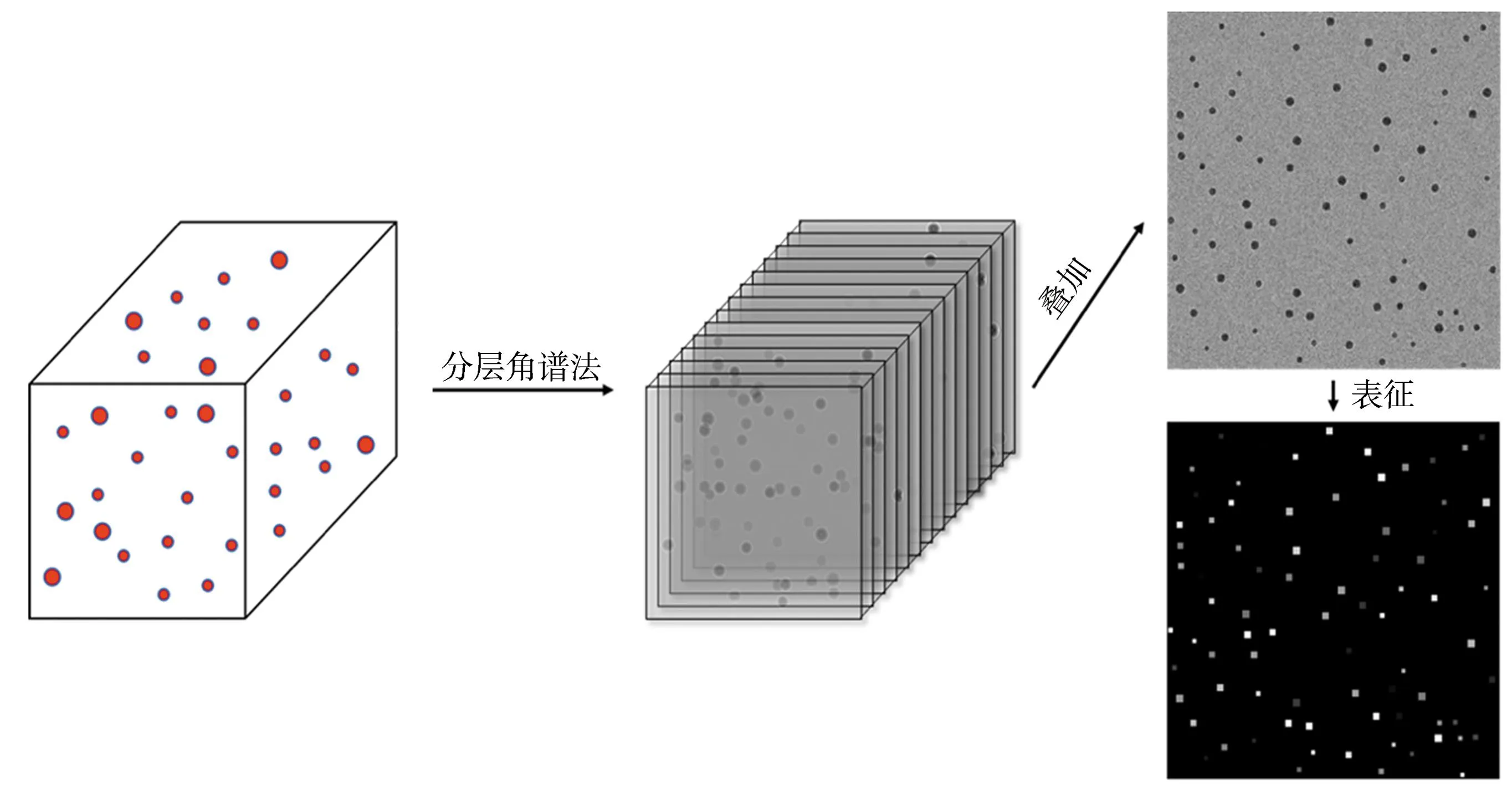
图1 粒子的模拟生成及表征

(7)

其中,2.048表示3D粒子场的深度范围(单位为mm)。

2 seFIN结构

近年来,随着神经网络的快速发展,它在光学成像领域的应用不断增加。经典的卷积神经网络(CNN)在成像任务中表现出卓越的能力,但它们仍然受限于感受野的大小。本文中,介绍了一种名为seFIN的网络,它使用傅里叶变换来将对象转化到频域,以有效处理全局空间频率信息,从而提高网络性能。

如图2所示,seFIN网络基于FIN架构进行了优化。其中,se注意力模块使模型能够更加专注于关键信息,加快模型收敛速度。该网络采用多级残差连接结构,提升了特征抽取效果。为减少深度增加带来的信息丢失,网络结合了多个SPAF组,每组包含se通道注意力模块、两个SPAF模块和一个卷积核大小为1的卷积层。通过残差连接,网络的容量得到增强,同时没有明显增加其大小。SPAF模块通过线性变换W来滤除频域张量中的高频信息,并通过窗口大小k截断高频信号:

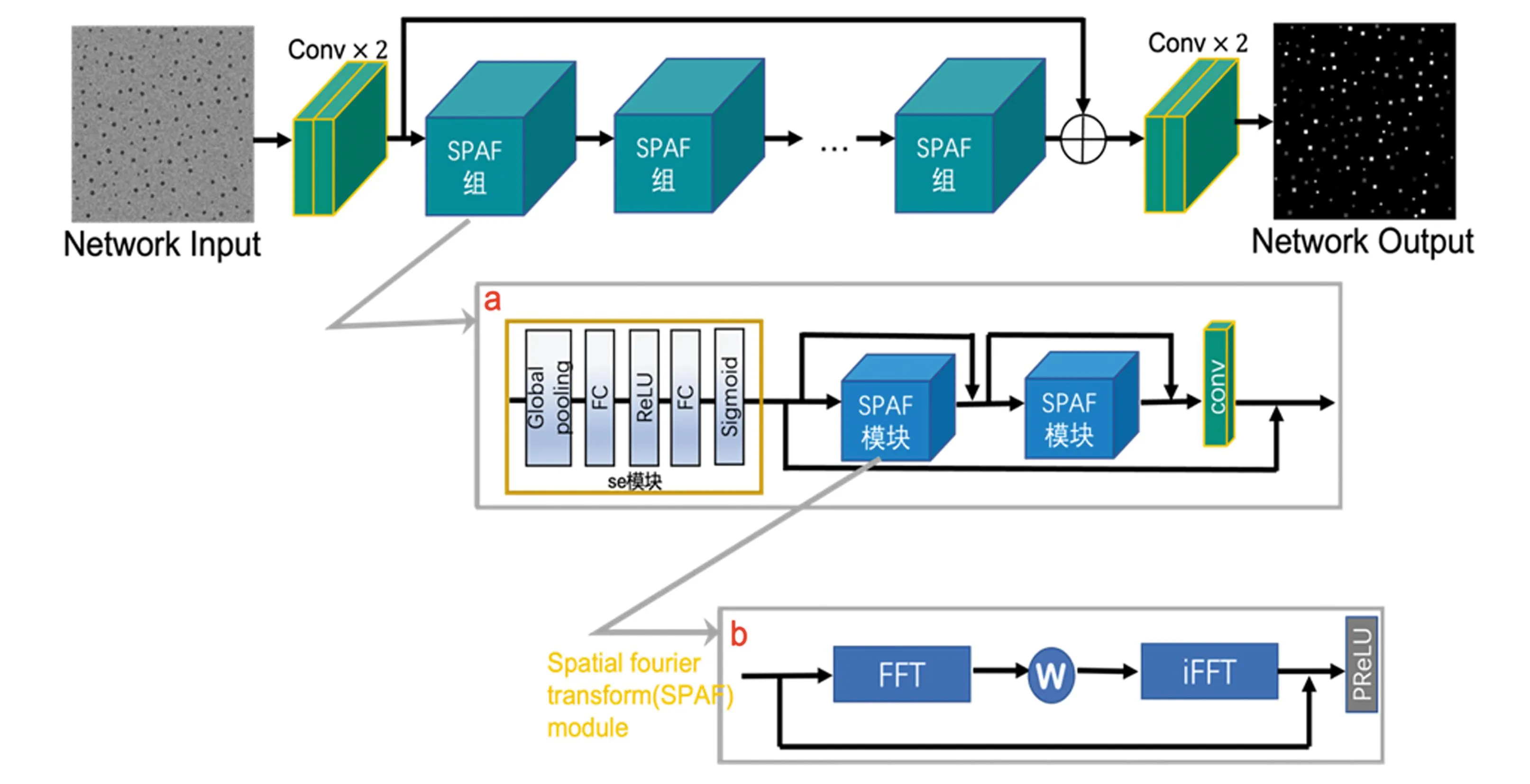
图2 seFIN架构

(8)

其中F∈c,2k+1,2k+1是表示输入到SPAF模块经过二维离散傅里叶变换后的截断频域表示;W∈c,2k+1,2k+1代表可训练权重;c是通道数,k为窗口大小。完成线性变换后,通过逆二维傅里叶变换将数据重新转换到空间域,并在之后使用PReLU作为激活函数:

(9)

a是一个可学习参数。

本实验使用了递减的窗口大小k,形成了一个金字塔状结构。这种结构可以将全息衍射图案的高频信息映射到前几层的低频区域,并以较小的窗口大小传递这些低频信息给后续层,从而更好地利用多个尺度上的特征,同时大幅减小模型大小,可以避免可能存在的泛化和过拟合问题。

其次对于3D粒子场全息实验,本网络所使用的损失函数:

Lloss=αLMAE+βLcomplex+γLpercep

(10)

(11)

(12)

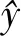
3 仿真结果分析

3.1 数据集及网络配置

网络的数据集分为训练集和验证集,通过模拟的手段生成数据集,包括8000张训练集和2000张验证集,以及使用(x,y,z,R)表征粒子对应标签图。seFIN网络训练了100个epoch,每个batch_size包含8000张图片。我们为这个网络设置了0.0001的学习率,因为在之前的实验中,这个值为我们的模型提供了最佳的验证性能。在我们的网络中,“残差深度”指的是网络中包含的残差块的数量,我们选择了22作为这个值,因为它为我们的特定任务提供了良好的性能。对于Dense_U_net,我们使用了一个batch_size包含8000张图片,并训练了800个epoch,学习率设置为0.001。

3.2 网络预测结果分析

如图3所示,我们对比了两种网络在不同颗粒子数量下(分别为75、150和300颗粒子)的预测结果。为了细致地对比,我们将预测结果进行了局部放大。在75和150颗粒子的场景下,两种网络的预测结果看起来非常接近。但在图3中,特定的黄色圆形区域标注出了一个被放大6倍的单一粒子。在这里,seFIN展示出了清晰的边缘,而Dense_U_net与真实值之间存在明显的差异,特别是粒子边缘的像素块显得模糊不清。然而,当粒子数量增加到300颗时,Dense_U_net的预测开始出现明显错误。相比之下,无论是在75、150颗粒子还是300颗粒子的场景中,seFIN都展现出了稳定而准确的预测,不论是图像的细节还是深度信息都与原图高度一致。

图3 seFIN和Dense_U_net网络的预测结果

3.3 评价函数

为了更直观地体现两种网络的差异通过使用评估图像质量的两种算法来评估网络预测的图像与原始图像之间的差异。表1是两种网络在不同粒子数量下的两种指标的结果。可以看出,在随着粒子数量的增加,Dense_U_net网络的SSIM指数逐渐下降,尤其到300颗粒子时明显下降,但是seFIN网络却保持在0.99内的一个稳定的数值,同样的seFIN网络的PSNR值无论哪种数量级的粒子始终高于Dense_U_net网络,从而可以得出seFIN网络在预测粒子方面性能始终优于Dense_U_net。

表1 seFIN与Dense_U_net预测图的SSIM和PSNR

3.4 粒子场重建结果分析

最后根据网络预测粒子信息重建粒子场,如图4所示,在粒子数量为75和150颗粒子时,两种网络的预测结果的准确率在95%以上,但是提升到300颗粒子,Dense_U_net只可以预测到位置(x,y)的信息,对于纵深z轴已经失去预测能力,反观seFIN网络依然可以准确地预测,且预测准确率依然在95%左右。

图4 seFIN和Dense_U_net根据预测信息重建粒子场后与真实粒子场对比

通过计算平均绝对差,我们比较了两种网络在预测粒子的横向和轴向位置以及大小的误差。具体的计算方法是:对每个粒子,取其原始值Aj和预测值Bj之间的差的绝对值,然后计算这些差的平均值。公式为

(13)

其中Aj和Bj是第j个粒子的原始值和预测值,P表示粒子的总个数。根据表2的数据,seFIN网络在75和150颗粒子的数据集上,无论是横向位置还是粒子大小,误差都为0,即完全准确。尽管在轴向位置的预测上存在5左右的误差,但相比Dense_U_net网络,仍有约55%的性能提升。在300颗粒子的数据集上,seFIN网络的横向位置和大小预测出现了轻微误差,但都小于0.1,而Dense_U_net在此数据集上的预测能力已经完全丧失。这表明在处理较大规模数据集时,seFIN网络显示出更强的鲁棒性和准确性。

表2 seFIN和Dense_U_net的预测粒子与原始粒子的平均绝对差值对比

4 实验验证

通过实验进一步验证网络的性能,图5展示了实验光路,其中采用激光的波长为532 nm,使用CMOS(MV-UBS500M,1944×2592,2.2 nm方形像素)捕获。通过捕获分布在乙醇溶液中的约200～300个聚苯乙烯颗粒(直径20 nm),生成同轴全息图。通过角谱法重建并结合手动阈值化及强度加权质心计算,我们获得了真实测量下的粒子位置。这些粒子的位置和大小被编码为2D矩形。我们的训练数据集由从全息图中随机裁剪的400张1024×1024像素的图片组成,并附带它们对应的粒子位置信息。为了增加样本多样性,我们采用了图像增强技术,如垂直和水平镜像,从而将训练数据集扩展到2500个样本。图6展示了粒子的三维分布,验证了该方法在真实复杂粒子预测上的有效性。并且如表3所示粒子的平均绝对误差,横向误差和大小误差均控制在0.3以内,这显著证明了横向位置和大小的高精度预测能力。尽管轴向误差最大达到6.56,但仍在可接受的范围之内,指明了未来研究的主要优化方向。

表3 预测粒子与原始粒子的平均绝对差值

图5 实验装置图

图6 通过seFIN对实验全息图重建结果

5 结论

本文介绍了一种通过傅里叶成像网络来重建粒子的三维位置的方法。该网络采用了空间傅里叶变换模块,并结合了可学习的滤波器和全局感受野,以快速而准确地处理全息图中的空间频率信息。相比传统方法,傅里叶成像网络不仅提高了数据处理的效率,而且具备了更强大的特征提取能力。这使其能够成功地表征和区分不同的颗粒特性。与Dense_U_net网络的预测结果相比,seFIN在不同数量级的粒子场的重建质量和准确率都表现得更为优越。