一维管网与二维地表双向耦合的城市暴雨内涝模拟

郑茂辉， 姚 帅， 周念清， 刘俊兵

（1. 同济大学 上海防灾救灾研究所，上海 200092；2. 同济大学 城市安全风险监测预警应急管理部重点实验室，上海 200092；3. 同济大学 水利工程系，上海 200092）

受人类活动和气候变化双重影响，国内外极端强降雨频发，城市内涝问题加剧［1-2］，特别是部分沿海城市受海平面上升和地面沉降影响面临着额外的内涝灾害风险［3］。探索准确、高效的城市内涝模拟方法对于预防和减轻城市内涝灾害具有重要意义。

城市内涝通常与排水系统能力不足有关［4］。欧美发达国家从20 世纪60 年代开始研制多种城市雨洪模型用来评估排水管网的水力特征，代表性模型有：美国环境保护署的暴雨洪水管理模型（storm water management model，SWMM）［5］、丹麦水力学研究所的城市水文模型（Mike Urban）［6］和城市排水系统模型（MOUSE）［7］、英国Wallingford公司的城市综合流域排水模型（InfoWorks ICM）［8］等。其中，SWMM 模型免费开源，对管网汇流计算表现良好，应用最为广泛。一维管网模型不能模拟二维地表积水扩散，结合水位-体积曲线方法能够确定积水深度及范围，但对于管网和上覆地面之间复杂的水力交互仍缺乏有效模拟手段。

为准确模拟城市区域暴雨内涝淹没过程，需要将一维管网模型与二维淹没模型进行结合［9-10］。一些商业软件，如MIKE Urban、XP-SWMM 和PCSWMM等，虽然实现了一维/二维水动力耦合模拟，但软件价格昂贵，且耦合机制未公开，一定程度上限制了其使用。一些学者［11-13］尝试结合SWMM和开源或半开源二维水动力模型，实现城市暴雨内涝过程模拟。例如，曾照洋等［12］耦合SWMM和半开源二维水动力模型（LISFLOOD-FP）［14］对东莞市某区域进行了洪涝模拟，结果表明耦合模型在研究区具有较好适用性；李鹏等［13］通过连接SWMM 和LISFLOOD-FP模拟了济南市某流域实测场次降水过程，取得了较好的模拟效果，认为耦合模型可用于城市流域暴雨内涝的模拟。以上研究通过SWMM管网模型和LISFLOOD-FP 淹没模型的单向连接，将管网节点溢流作为点源边界条件驱动LISFLOOD-FP 模型，实现过程相对简单、易用，但忽略了管网节点的地表积水回流，内涝模拟结果可能趋于严重。

本文提供了一种基于开源暴雨洪水管理模型接口（PySWMM）［15-16］实现一维管网模型与二维淹没模型双向耦合的方法，构建SWMM/LISFLOODFP耦合模型，实现排水管网及其上覆地表的双向水量交换，并利用上海市浦东外高桥地区的两次降水序列对耦合模型进行校验，同时对比单向和双向2种耦合方式的模拟结果，验证模型的适用性和精确性。

1 模型方法

所构建的SWMM/LISFLOOD-FP 双向耦合模型中，SWMM 模型用于产汇流和一维管网模拟计算，LISFLOOD-FP模型则用于地表二维淹没模拟。一维和二维模型以管网的检查井为连接点，通过节点溢流和回流实现管网和地表的双向流量交互，其中节点溢流量通过PySWMM 提取，回流量采用堰流和孔口流量公式确定；一维模型采用固定时间步长，二维模型采用可变自适应步长，二者通过时间同步实现步长级数据交换。

1.1 SWMM管网模型

SWMM 模型是一个降雨径流水量和水质分析的综合性计算机模型，由水文、水力及水质三个主要模块组成，可以实现地表产汇流、管网一维水动力模拟以及水质模拟。其中，地表产流可选择霍顿（Horton）下渗模型、格林-安普特（Green-Ampt）下渗模型和径流曲线法（soil conservation service curve number method，SCS-CN）模拟下渗过程，地表汇流采用非线性水库法，管网一维水动力可选择运动波或动力波模拟。SWMM 能够模拟汇水区域、检查井、管道等水文和水力要素的时空分布［17］，具有适用性良好、开源和应用简便等优点，在城市排水系统模拟中得到了广泛应用［18］。本文重点考虑暴雨、径流、内涝的关系，未将水质模拟纳入到此项研究之中。

雨水管网汇流计算采用一维非恒定流模型，通过连续性方程和动量方程联立求解：

式（1）—（2）中：Q为管道中的流量，m3·s－1；A为过流断面的面积，m2；S0为管道坡度，P为湿周长，m；n为曼宁摩擦系数；h为水流深度，m。

1.2 LISFLOOD-FP淹没模型

LISFLOOD-FP 模型是英国布里斯托大学Bates 等人开发的一种基于栅格计算的二维水动力模型［14，19］，该模型可以和高精度的数字高程模型（digital elevation model， DEM）结合，在低海拔洪泛平原区适用性较好，是一种简单可靠的二维洪水淹没模型［20］。经过不断的升级更新，近年来LISFLOOD-FP模型在城市内涝模拟中也得到应用和推广。

采用LISFLOOD-FP的洪泛区求解器模拟地表汇流，将二维地表水流运动离散到正方形栅格上，用连续性方程和动量方程描述：

式（3）—（4）中：t为时间，s；Qup、Qdown、Qleft、Qright分别为来自上游、下游、左边和右边栅格单元的流量，m3·s－1；当前时间步长某栅格单元的水量变化等价于其4 个邻接栅格的流量累加；Qij为相邻栅格单元i，j交界处的流量，m3·s－1；Aij为相邻栅格单元i，j交界处的截面积，m2；Rij为i，j栅格交界处的水力半径，m；Sij为相邻栅格i和j之间的水面坡度；n为曼宁系数。

1.3 模型耦合

1.3.1 模型耦合原理

一、二维水动力模型的耦合可分为单向耦合与双向耦合。单向耦合将一维管网模型（SWMM）的节点溢流过程作为点源边界条件驱动二维淹没模型（LISFLOOD-FP）（图1a），该耦合方式不考虑管网节点回流，数据单向传递。双向耦合则是将一维、二维模型分步模拟，互为驱动（图1b），该耦合方式不光考虑管网节点溢流，地表积水也可通过节点回流到地下管网，数据双向交互。

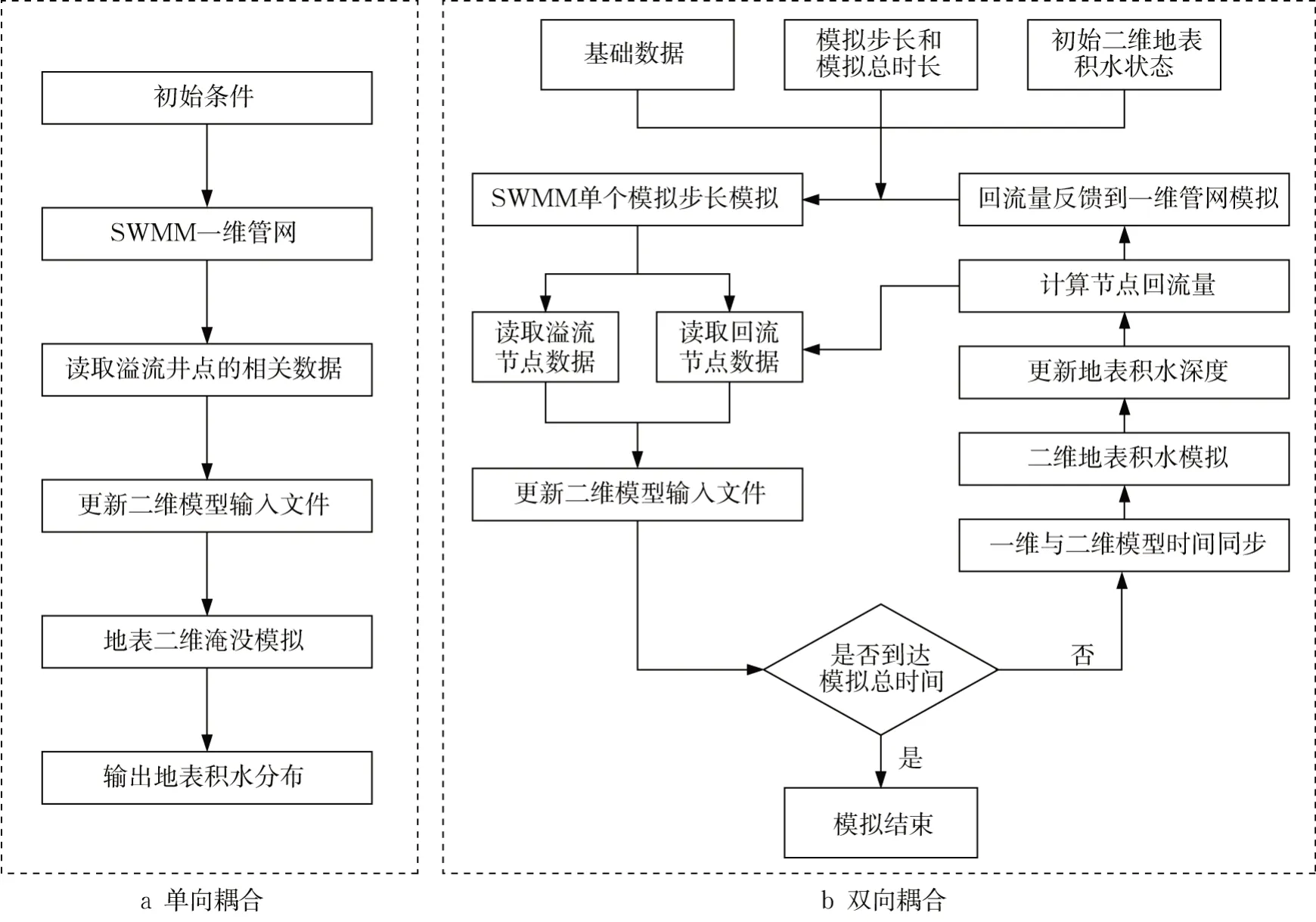
图1 模型耦合原理及过程Fig. 1 Coupling principle and process of models

美国环境保护署的SWMM 模型不具备在运行过程中读取模拟结果和交互数据的功能，通常需要修改模型源代码方能实现其同二维水动力模型的数据互操作，本文选择基于SWMM5 开发的第三方开源库PySWMM，实现任意时间步长模拟结果的读取，通过开发控制算法对节点流量交换实现步长级控制。

双向耦合模型通过发生溢流或回流的节点连接一维管网模型和二维淹没模型，实现双向数据交换。当降雨强度超过管网排水能力时，管网中的水量通过超载节点溢流到上覆地表；相反，当管网排水能力充足时，地面积水通过对应的井点回流到地下管网中。双向耦合模型主要由4个模块组成，（1）SWMM一维管网模拟：SWMM模型每完成一个步长模拟，均记录发生溢流或回流的井点坐标、水深和流量（溢流为正，回流为负），作为点源边界驱动二维淹没模型；（2）LISFLOODFP二维淹没模拟：接收一维管网模型的节点流量，模拟二维地表漫流，更新地表积水深度；（3）一维和二维模型的数据交互：两个模型通过节点溢流和回流进行双向流量交换，溢流量通过PySWMM读取，回流量采用堰流或孔流公式计算；（4）一维和二维模型的时间同步：一维、二维模型以串行方式连接，耦合模型每完成一个时间步长的模拟即进行数据交互，必须保证将两个模型的时间同步。

1.3.2 双向流量交互

一维、二维模型通过检查井连接地下管网和地表栅格单元，进行双向水量交换。假设管网节点水头为hw，其对应的地表栅格单元水位为h2d，则有如下垂向流量交换：①hw＞h2d，管网中水流由节点溢出到地表；②hw＜h2d，地表水由节点回流到地下排水管网；③hw=h2d，或地表无积水，则地下管网和地表不存在垂向水量交换。

目前关于地下管网和地表的垂向水流交换的基础理论尚不成熟，计算方法也较为有限［21］。本文通过PySWMM 编程获取每个时间步长溢流节点的流量，而节点回流量则采用堰流公式和孔口流量公式计算。假定井口地表高程为hz，概化井口过水面积A=BL，其中B表示过水断面宽度，L表示过水断面长度。节点回流计算方法如下：

（1） 当h2d＞hz＞hw时，节点回流量采用自由堰流公式计算：

式中：Q为当前时间步长的节点回流量，m3·s－1；cw为堰流流量系数，取值［0，1］；g为重力加速度，m·s－2。

（3） 当h2d＞hw＞hz且（h2d-hz） ＞L时，节点回流量采用孔口流量公式计算：

式中：co为孔口流量系数，取值［0，1］。

1.3.3 时间同步

一维、二维模型的时间同步是数据双向交互的重要前提。本研究中管网汇流和地表淹没模拟采用独立的动力学模型，其中一维管网模型采用固定的时间步长，二维淹没模型采用的是可变自适应时间步长，因此需要将一维、二维模型的时间步长进行同步匹配。

如图2 所示，将耦合模型总模拟时长T0划分成多个等时长间隔，每个等时长间隔即为一维模型的一个固定时间步长Δt1D，同时对应二维模型的一个模拟批次的模拟时长ΔT2D，每个二维模拟批次包含若干自适应时间步长（ΔT2D=ΣΔt2D）。二维模型运行过程中通过设置“检查点”属性，使得下一个批次的模拟计算可以继承上一个批次模拟结束时的水力状态，由此实现一维模型固定时间步长和二维模型可变步长的时间同步。

图2 一维和二维模型时间同步Fig. 2 Time synchronization between 1D and 2D models

式（8）—（9）中：T0表示耦合模型的总模拟时长，s；Δt1D表示一维模型的固定时间步长，s；ΔT2D表示二维模型一个批次的模拟时长，s；Δt2D表示二维模型的自适应时间步长，s。为确保数值模拟的稳定性，自适应时间步长可基于克朗 （Courant-Friedrichs-Lewy，CFL）条件进行估算［22］。

2 应用案例

2.1 研究区与数据

受亚热带季风气候影响，上海雨量充沛，年平均降水量约为1 200 mm，且60 %的雨量集中在5 至9月。本文研究区位于上海市浦东新区北部，长江入海口南侧，整体地形平缓，海拔4～5 m，区域面积为5.56 km²。北侧和东侧为外环运河，西侧和南侧分别以主干道杨高北路、洲海路为界（图3a）。该区为上海外高桥保税区核心区域，建筑物密集，地面硬化程度高，遭遇强降雨时易因排水能力不足造成积水内涝。

（二）分析电路图，找到问题与已知条件间的关系。在做电学题时，要在读清题之后，仔细的分析电路图，先要正确的判断电路的串并联情况。教师可以用去掉一个用电器的方法，教学生正确的判断电路。若去掉用电器后，电路相互影响则为串联，若不会相互影响，则为并联。其次要找清楚电表测量的对象，在看电压表时，可以观察他并联在谁的两端，就是测谁的电压。在判断电流表时，可以去掉电流表，看哪个用电器被影响到就是测谁的电流。最后根据欧姆定律，运用所学的电学公式解题。

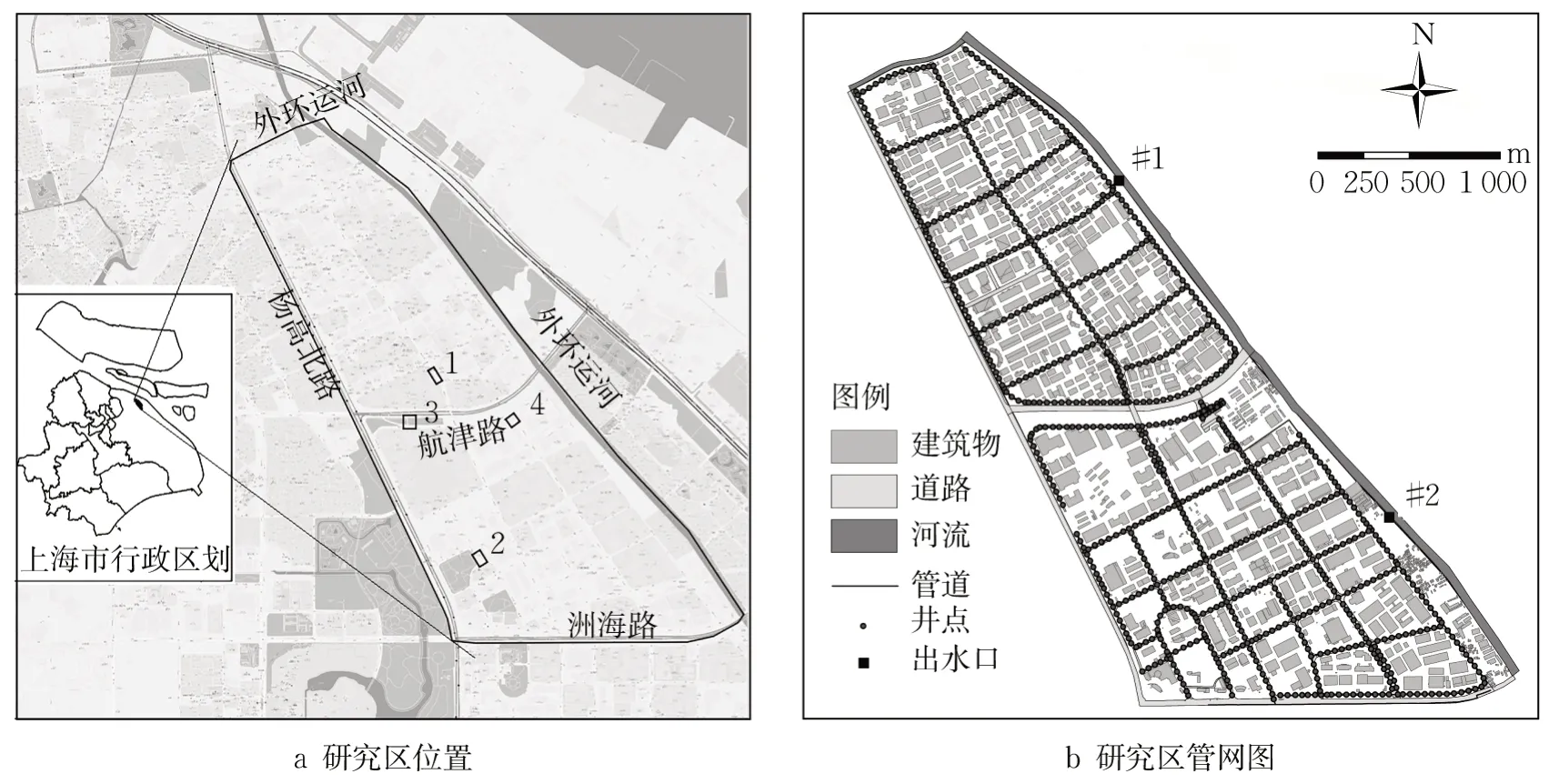
图3 研究区位置与排水设施分布Fig. 3 Location and distribution of drainage facilities in the study area

本文采用研究区2015 年的土地利用数据和排水管网数据， DEM 的分辨率为2 m×2 m。考虑到建筑物对地面积水的阻挡作用，采用设定高程法，在ARCGIS（地理信息软件）中将建筑物矢量图层转化为2 m×2 m栅格数据，叠加到DEM上，并根据建筑物分布修正地面高程。研究区排水管网设计暴雨重现期为1 年，自2010 年以来未有过系统性更新和改造。管网以航津路为界分为南、北两个部分，互不相连，汛时主要依靠东部边界2 个雨水泵站抽排至外环运河，汇入长江口。图3 b 给出管网概化图，共包括检查井925 口，管道987 根、泵站排水口2 个。根据管网连通状况，将研究区划分上下2 个一级子汇水区；利用泰森多边形进一步划分二级子汇水区，确保每个二级子汇水区对应一个检查井节点。采用2013 年8 月4 日（20130804）和2013 年9 月13 日（20130913）两次短历时暴雨过程对模型进行校准和验证，降雨数据源自研究区高东雨量站，积水数据采用图3 a中4个位置调研的积水深度数据。

2.2 模型校验

模型经验参数取值参考SWMM用户手册［23］，采用“20130804”场次降雨过程以及实测积水数据对管道曼宁系数、霍顿下渗参数、孔口系数、堰流系数等敏感性参数进行率定。利用“20130913”场次降雨验证模型，该场次降雨强度较大，降雨量主要集中在15：30～17：30，2 h 降雨量占全天总降雨量的97 %。大暴雨导致浦东中北部地区内河水位急剧上涨，其中外高桥内河水位达3.18 m，多条马路短时积水20～50 cm。

采用双向耦合模型对“20130913”场次降雨进行模拟，模拟时长为6 h。图4a给出降雨过程和两个出水口的流量过程线。与降雨双峰曲线不同，2个出水口流量过程基本上均呈单峰特征，涨洪段较陡，流量峰值出现在第2次雨量峰值后30～60 min，在降雨停止后流量持续走弱。提取图4b中4个监控点位的最大水深数据，与调研水深对比以验证模拟结果。由表1可知：模拟水深与调研结果较为接近，说明模型在该片区具有较好的适应性，模拟结果较为可靠。

表1 模拟积水深度与实测结果对比Tab. 1 Comparison of simulated ponding depth with measured depth

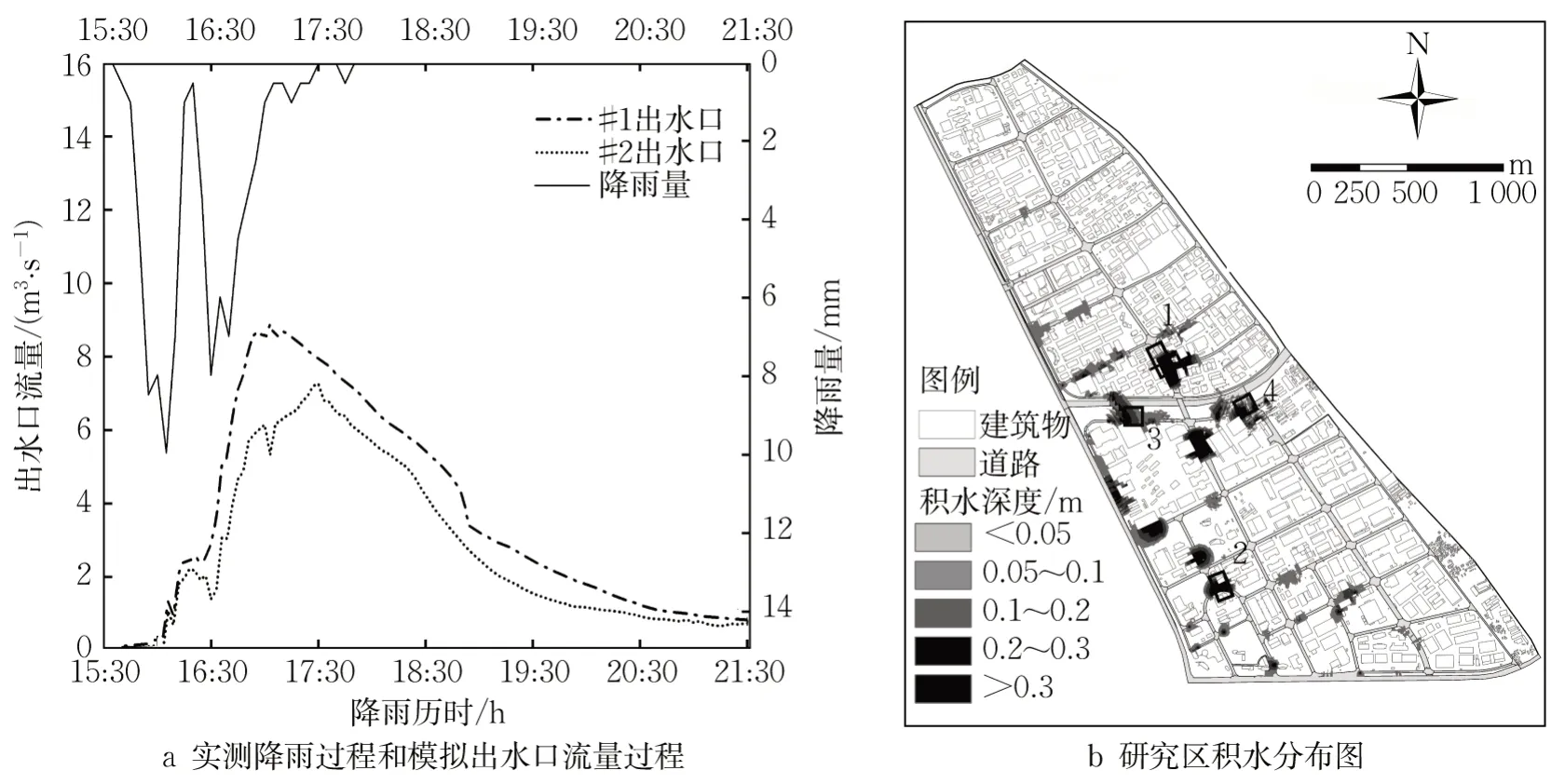
图4 研究区“20130913”场次降雨模拟结果Fig. 4 Measured rainfall process and simulated water outlet flow process

2.3 模拟结果分析

分别采用单向、双向耦合方式对“20130913”场次降雨进行模拟，对比2 种耦合方式的积水面积和水深分布，并对2 种耦合方式的模拟计算效率进行了比较。

2.3.1 最大积水分布范围对比

图5a、图5b给出单向和双向耦合的最大积水分布图，两者最大积水面积分别为27.21×104m2和21.07×104m2，交集区域（图5c）面积达17.67 ×104m2，2种耦合方式对内涝淹没范围的预测重叠率较高。由表2不同积水深度的面积统计结果发现，对于占比80 %以上、水深0.2 m以下的轻度积水区域，单、双向耦合的模拟积水面积相近，前者约为后者的1.21倍，但对于中等（0.2～0.3 m）和严重（＞0.3 m）积水区域，该比值分别达到1.88和2.1。可见，相对于双向耦合，单向耦合的模拟积水范围，特别是对于水深0.2 m以上积水区域的预测结果趋于严重。此外，尽管单向耦合的模拟积水面积为双向耦合的1.3倍，但前者出现溢流的节点却略少于后者。这应与单向耦合未考虑管网节点回流有关，即降低了排水管网超载的压力。

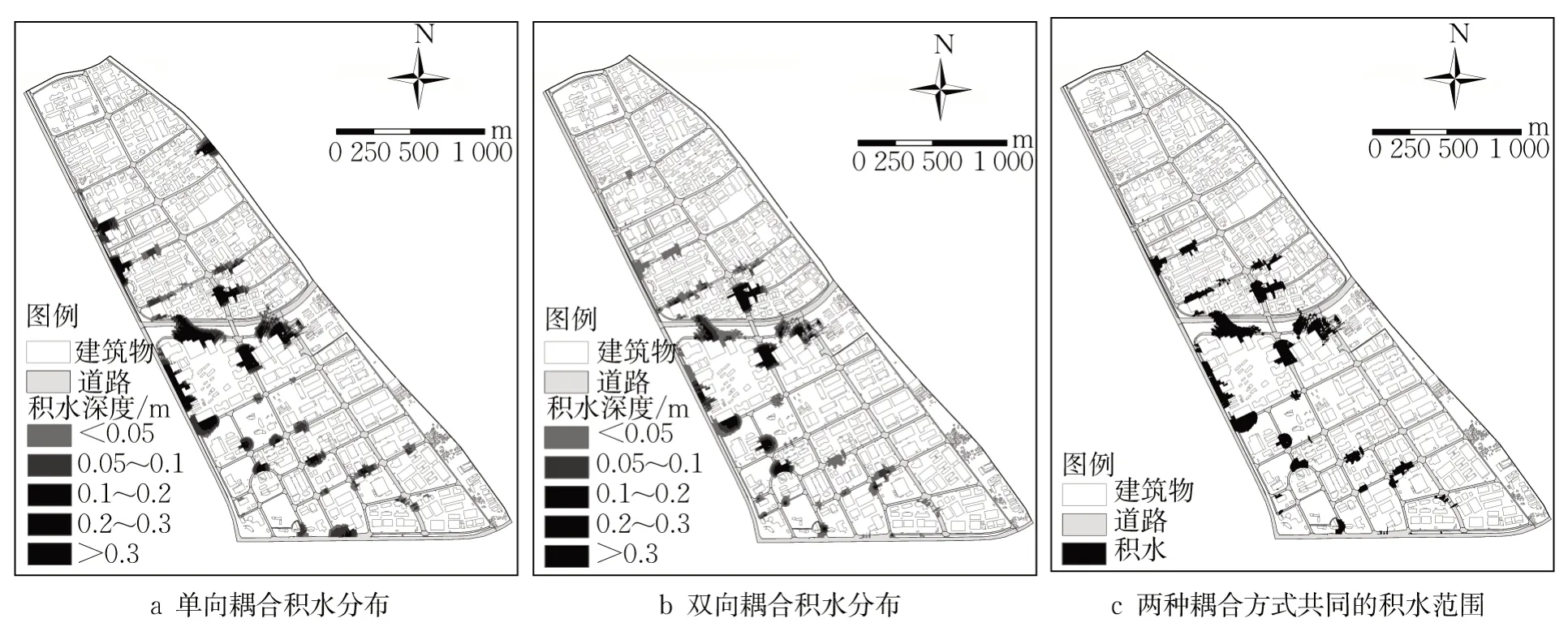
图5 单向和双向耦合最大积水分布图Fig. 5 Maximum water accumulation area

2.3.2 积水面积与水深动态变化

为定量分析2种耦合方式模拟的积水面积和水深动态变化，图6 给出了积水面积和最大水深随时间的变化曲线。结果表明：

图6 积水面积与最大水深随时间变化曲线Fig. 6 Time-varying curves of stagnant water area and maximum water depth

（1）在2次雨峰之后即17：00左右，模拟积水面积达到峰值；其后，单向耦合的积水面积基本保持稳定，双向耦合则更如实反映了地表积水的消退过程（图6a）。

（2）不同于积水面积过程曲线，水深变化曲线具有明显的双峰特征，与降雨过程相符（图6b）。单向和双向耦合方式模拟最大水深分别为0.79 m 和0.61 m，水深峰值时刻出现在雨峰后的20～30 min，且单向略滞后于双向（表3）。

表3 单向和双向耦合模型结果对比Tab. 3 Comparison of result between unidirectional and bidirectional coupling models

（3） 17：30 后单向耦合最大模拟水深基本保持在0.3 m，双向耦合最大水深则在18：00 后降至0.2 m以下，并逐渐消减。对照2种方式模拟结果 ，双向耦合模拟的积水范围与水深变化与研究区9.13 暴雨内涝报道情形基本一致，能够更好揭示城市内涝积水以及扩散、消退的全过程。

这一差异增加了双向耦合的一维模拟计算量。不过考虑到双向耦合数据交互耗时与计算总时长及步长大小有关，对耦合模型总体运行效率的影响尚需进一步探讨。

2.3.3 单、双向耦合计算效率对比

2种耦合方式固定时间步长均设为30 s、模拟时长为6 h，在同一工作站配置计算环境下对模型运行耗时进行对比。由表4结果可知：在一维模拟阶段，双向耦合的计算耗时是单向耦合的1.8 倍；但在二维模拟阶段，双向耦合计算耗时要略低于单向耦合；总模拟耗时双向耦合稍大于单向耦合，约为后者的1.1 倍。2 种耦合方式的计算耗时差异原因在于模型运行原理不同：单向耦合模式下一、二维模型可独立运行，一维模型中管网节点溢流驱动二维水力计算；双向耦合模式中一维和二维模型需要进行数据双向交互，互为驱动。

表4 耦合模型计算时间对比Tab. 4 Comparison of calculation time between two coupling models

3 结语

城市下垫面建筑物和基础设施密布、排水系统立体式分层结构显著，使得城市的产汇流机制远比天然流域复杂。为快速、准确模拟城市区域暴雨产汇流过程，本文提供了一种一维管网与二维地表的动态水力交互方法，构建了SWMM/LISFLOODFP双向耦合模型。以上海外高桥地区为例，采用两场次降雨过程对耦合模型进行了校准和验证，并对比了单向耦合和双向耦合的模拟结果，主要结论如下：

（1）所构建的双向耦合模型通过时间同步实现了一维/二维模型之间步长级的流量交换控制，能够较好地模拟地下排水管网与上覆地表之间复杂的水力交互。对实测场次降雨过程的模拟结果表明，该耦合模型具有较好的精度，在研究区适用性良好。

（2）比较单向耦合和双向耦合模拟结果发现，对于占淹没区域80 %以上的轻度（＜0.2 m）积水区二者模拟积水面积接近，对于水深0.2 m 以上的积水区，单向耦合模拟结果则相对趋于严重，约为后者的1.9倍。降雨结束后，双向耦合的积水面积和水深随着积水消退而逐渐减小，更好揭示暴雨积涝的全过程。在计算效率上，双向耦合增加了数据交互耗时，但二维模拟阶段用时略有下降，后续需结合时间步长设置进一步讨论，并通过图形处理器（GPU）高性能计算进一步提升运算效率。

（3）值得补充说明的是，本文采用开源PySWMM 和半开源LISFLOOD-FP 构建了双向耦合模型，该方法同样可选择其他水动力模型进行双向耦合，耦合模型及成果可用于城市区域暴雨内涝数值模拟及推演，为城市防洪和内涝治理措施的制定提供科学依据。

作者贡献声明：

郑茂辉：耦合模型总体设计，论文修改与定稿。

姚 帅：算法实现，论文初稿撰写。

周念清：指导论文框架，协助论文修改。

刘俊兵：协助数据处理与分析。