低成本航空发动机控制器的低温加热设计及优化
2024-03-04邓淼森胡春艳孙嘉娴陈弘扬
邓淼森,胡春艳,孙嘉娴,陈弘扬
(1.中国科学院工程热物理研究所 轻型动力重点实验室, 北京 100190; 2.中国科学院大学 航空宇航学院, 北京 100049)
0 引言
导弹、巡飞弹、靶机等飞行器使用的航空发动机属于消耗性产品,具有寿命短、需求量大的特点,这使得该类航空发动机对成本因素较为敏感。控制器是航空发动机的重要组成部分,其低成本化是降低航空发动机总成本必不可少的环节之一。
采用商用现货(commercial-off-the-shelf,COTS)元件开发航空发动机控制器是降低成本的重要技术途径[1]。COTS元件是指可以直接从民用市场购买的元件,如汽车级/工业级元件。相比于军品级元件,COTS元件具有成本低廉、供货稳定、研发周期短等优点,但是其可靠性与环境适应性较差,这给COTS元件在航空电子设备中的应用带来了诸多困难。为解决这些问题,国内外学者开展了相关研究,目前在器件筛选、性能评估、容错控制、冗余设计等方向[2-6]已经有了一些研究成果,而环境防护方面的研究相对较少。
航空发动机控制器需要在-55 ℃的环境温度下稳定工作,而汽车级/工业级元件的最低工作温度为-40 ℃。如果在超出额定温度范围的情况下使用,元件的可靠性、稳定性、寿命等都会受到影响[7],这对于直接关系到飞行安全的航空发动机控制器而言是无法接受的。因此,加热设计对于低成本航空发动机控制器在低温环境中的稳定工作起着重要作用。
张娅妮等[8]设计了一种基于电阻加热膜的加热电路并进行了板级试验,试验结果表明,该加热方法能够满足机载电子设备的低温加热需求。张先锋等[9]提出了一种印制电路板(printed cir-cuit board,PCB)内埋薄膜电阻的加热方法,该方法将加热功能集成至PCB中,不需要添加额外的附件,有利于电子设备的小型化、轻量化设计。尹可等[10]通过在PCB走线层布置导线来实现加热功能的集成化设计,相比于张先锋的内埋电阻方法,PCB内置走线加热层对PCB加工工艺的要求更低。聂营等[11]在电动机控制器中安装一块加热板以维持控制器内部温度,在稳态情况下,该方法可以保证元件维持在额定温度范围内。
目前针对系统级电子设备低温加热的研究比较有限,大多数文献相关研究的分析与验证工作都局限在电路板级,其实用性有待商榷;少数系统级研究虽然对低温加热有所涉及,但仅仅只是做了简单介绍,并没有针对该部分展开深入探讨。
针对现有研究的不足,本文中以某低成本航空发动机控制器为研究对象,设计了一种基于PI加热膜的加热方案,使用ANSYS Icepak对该方案的加热效果进行了数值仿真分析,并在低温试验箱内完成了实验验证。为了解决主板元件在升温过程中温度均匀性差的问题,本文中提出了一种基于遗传算法的加热膜几何形状优化方法,并对主板加热膜进行了优化设计。
1 加热方案设计
PI加热膜厚度薄、质量轻、电阻温度系数小,且可以根据使用需求定制尺寸形状、工作电压、加热功率等参数,能够很好地满足航空发动机控制器的低温加热需求。基于上述原因,本文中选择PI加热膜作为加热器,将其贴附在电路板表面。由于加热膜必须完全贴合在被加热物体表面,两者之间不能存在气隙,因此,加热膜只能布置在电路板表面没有元件的区域。如图1所示,电路板共3块,包括接口板、电源板和主板,加热膜形状根据元件分布情况进行定制。

图1 加热方案示意图
根据GJB/Z 457机载电子设备通用指南[12]的规定以及汽车级/工业级元件的最低工作温度,将加热目标定为:环境温度-55 ℃、控制器未上电(元件自身不发热)的情况下,在升温阶段,应保证120 s内将控制器中所有元件加热至-40 ℃以上;在恒温阶段,应保证控制器中所有元件的稳态温度在-40 ℃以上。
2 仿真分析与实验验证
2.1 几何模型
2.1.1机箱
机箱材质为铝合金,整体尺寸为152 mm(L) × 147 mm(W) × 40 mm(H)。机箱上的倒角、螺孔和密封凹槽等细节对仿真结果影响很小,在建模时进行了简化。简化处理有利于网格划分时减少网格数量、提高网格质量。
2.1.2PCB
PCB采用ECAD模型进行建模。ECAD模型根据PCB的过孔、布线等实际结构来计算得到PCB的物性参数,能够准确地反映出PCB各布线层的物性参数分布情况,效果如图2所示。
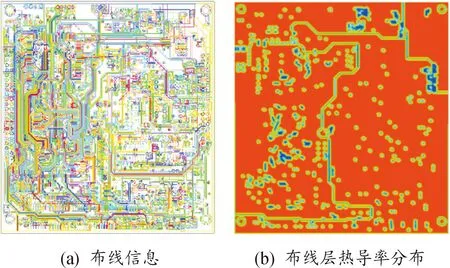
图2 ECAD模型示意图
2.1.3元件
对于体积较小的电阻、电容、磁珠等元件,建模时予以忽略。其余元件采用块模型,材料性质参考FLOMERICS公司的典型集总封装(typical lumped packages)材料库,具体数值见表1。
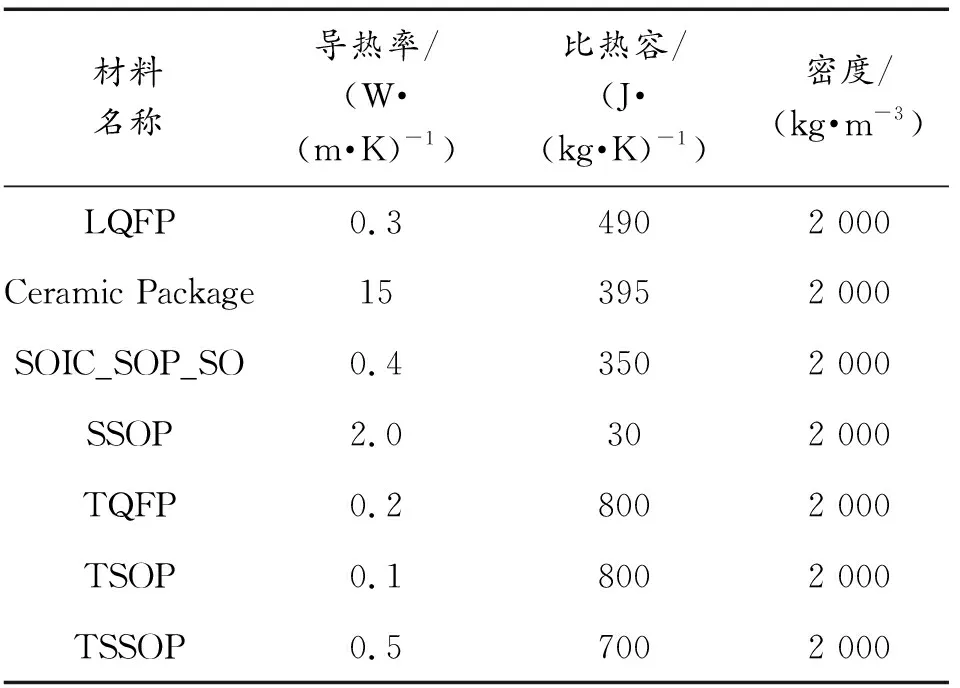
表1 典型集总封装材料性质
2.1.4其余几何模型
加热膜内部布线排列紧密、分布均匀,因此将加热膜简化为均匀发热的热源,表2中列出了加热功率的分配情况。
按照低温试验时的换热情况进行计算域建模,控制器外部为大空间自然对流换热,为保证数值计算的精度,参考文献[13]中的自然对流计算域设置准则,将计算域尺寸设置为400 mm(L)×400 mm(W)×400 mm(H),以确保远场处的变量梯度足够小,整体视图见图3。控制器被放置在一块泡沫板上,泡沫板热物性参数如下:导热率0.03 W/(m·K)、比热容2 300 J/(kg·K)、密度30 kg/m3。
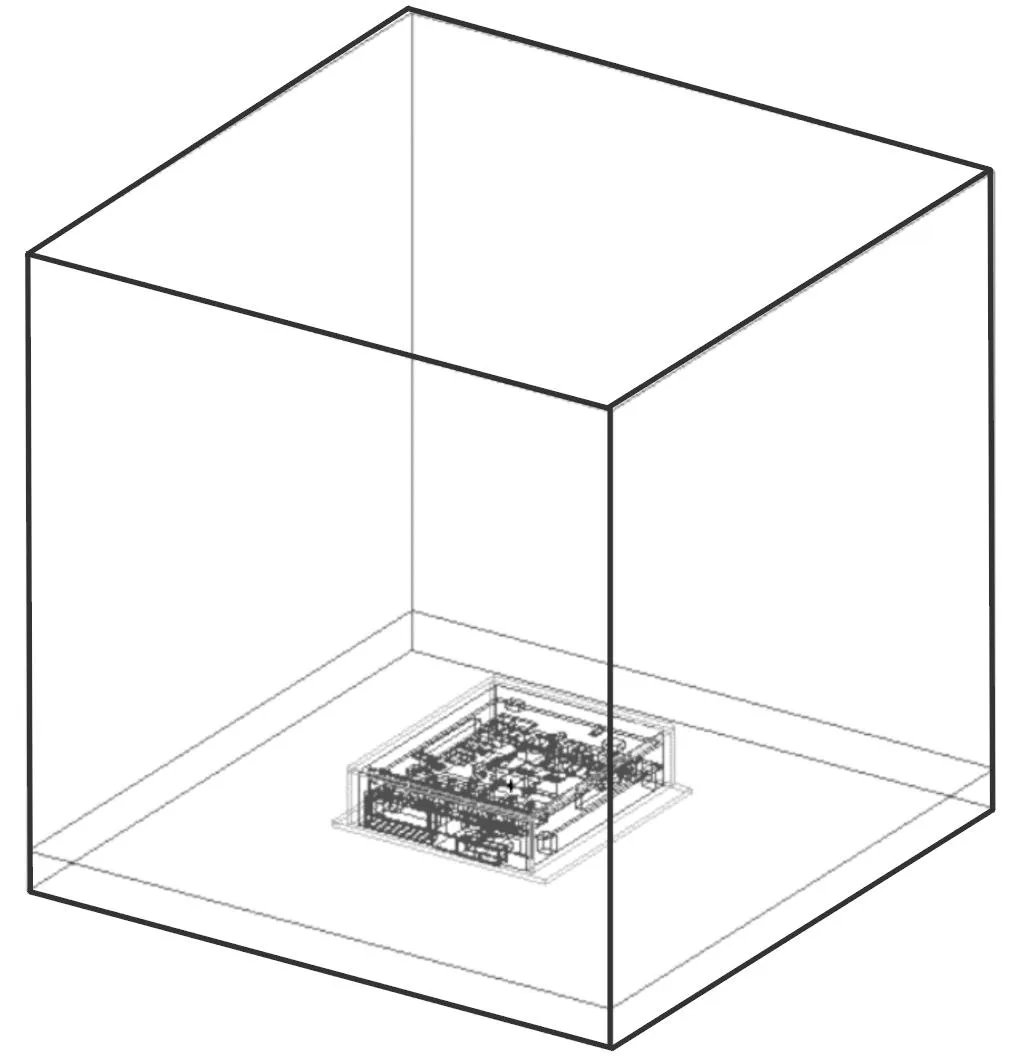
图3 几何模型整体视图
2.2 边界条件与求解器设置
恒温阶段算例进行稳态仿真,计算域底部边界设置为无滑移恒温壁面,其余5个边界设置为opening边界,环境温度-55 ℃。升温阶段算例进行瞬态仿真,边界条件与恒温阶段算例相同,设置初始速度为0 m/s,初始温度为-55 ℃,时间步长0.1 s,计算终止时间120 s。
加热过程中,控制器外部的空气进行自然对流,瑞利数在105量级,处于层流流态;控制器与外部空气进行小温差换热,采用Boussinesq假设来引入密度差产生的浮力效应;辐射换热采用离散坐标法进行求解;收敛残差、离散格式、松弛因子等参数采用Icepak默认设置。
2.3 网格划分
将计算域分为3个部分:控制器内部区域、机箱及近壁流体区域、背景区域。采用Mesher-HD网格对各区域进行非连续网格划分,各区域的网格尺寸根据区域内几何模型的尺寸进行相应设置,在变量梯度较大的区域进行网格局部加密,网格数量330万,划分结果见图4。

图4 网格示意图
2.4 仿真结果与分析
图5为恒温阶段的仿真结果,总加热功率为10 W。机箱的温度分布非常均匀,稳定在-30 ℃左右;各电路板上元件的稳态温度(取元件中心处温度)在-25~-13 ℃范围内。稳态情况下,电路板的温度均匀性受电路板导热率影响,从温度分布图中可以发现,热量可以在电路板水平方向进行有效扩散,加热膜覆盖区域的温度会略高于未覆盖区域的温度,但总体而言,各电路板元件的温度均匀性较好:接口板元件温度范围-24~-21 ℃,电源板元件温度范围-26~-20 ℃,主板元件温度范围-19~-14 ℃。
图6为升温阶段第120 s时的仿真结果,总加热功率为70 W。经过2 min的加热,机箱温度上升至-50 ℃左右;各电路板上的元件均被加热至-40 ℃以上。升温过程中,电路板的温度均匀性受电路板的热扩散系数影响,热扩散系数由导热率、密度和热容共同决定,因此,升温过程中电路板的温度分布可能会与恒温阶段的温度分布有较大差异。对各电路板元件在第120 s时的温度(取元件中心处温度)进行了统计:接口板元件温度在-32~-17 ℃范围内,电源板元件温度在-36~-10 ℃范围内,主板元件温度在-26~+24 ℃范围内。从仿真结果可以看出,主板中心区域的元件与边缘区域的元件出现了较大的温差,这主要是因为加热膜集中布置在主板中心区域,主板在水平方向上的导温能力不足以将中心区域的温度变化及时地扩散至边缘区域。

图5 恒温阶段温度分布图

图6 升温阶段温度分布图(第120 s)
2.5 实验验证
为验证仿真结果的准确性,在低温试验箱内进行了实验。温度传感器为T型热电偶,共布置5个测点;实验过程中,低温实验箱目标温度设置为-55 ℃。测点位置以及实验环境见图7。

图7 实验配置
恒温阶段实验结果在加热膜通电3 h后测得,此时测点温度已达到稳态,实验与仿真结果对比如表3所示。

表3 恒温阶段实验与仿真结果
升温阶段实验结果取加热膜通电后120 s内的数据,每秒采集1次数据,实验与仿真温升曲线如图8所示。

图8 升温阶段实验与仿真结果
实验数据和仿真数据的对比结果表明,仿真结果能够反映各PCB及元件的实际温度分布情况,仿真模型是可靠的。
3 加热膜几何形状优化
为解决主板元件在升温过程中的温度不均匀问题,采用遗传算法对主板加热膜的几何形状进行了优化设计,优化流程见图9。
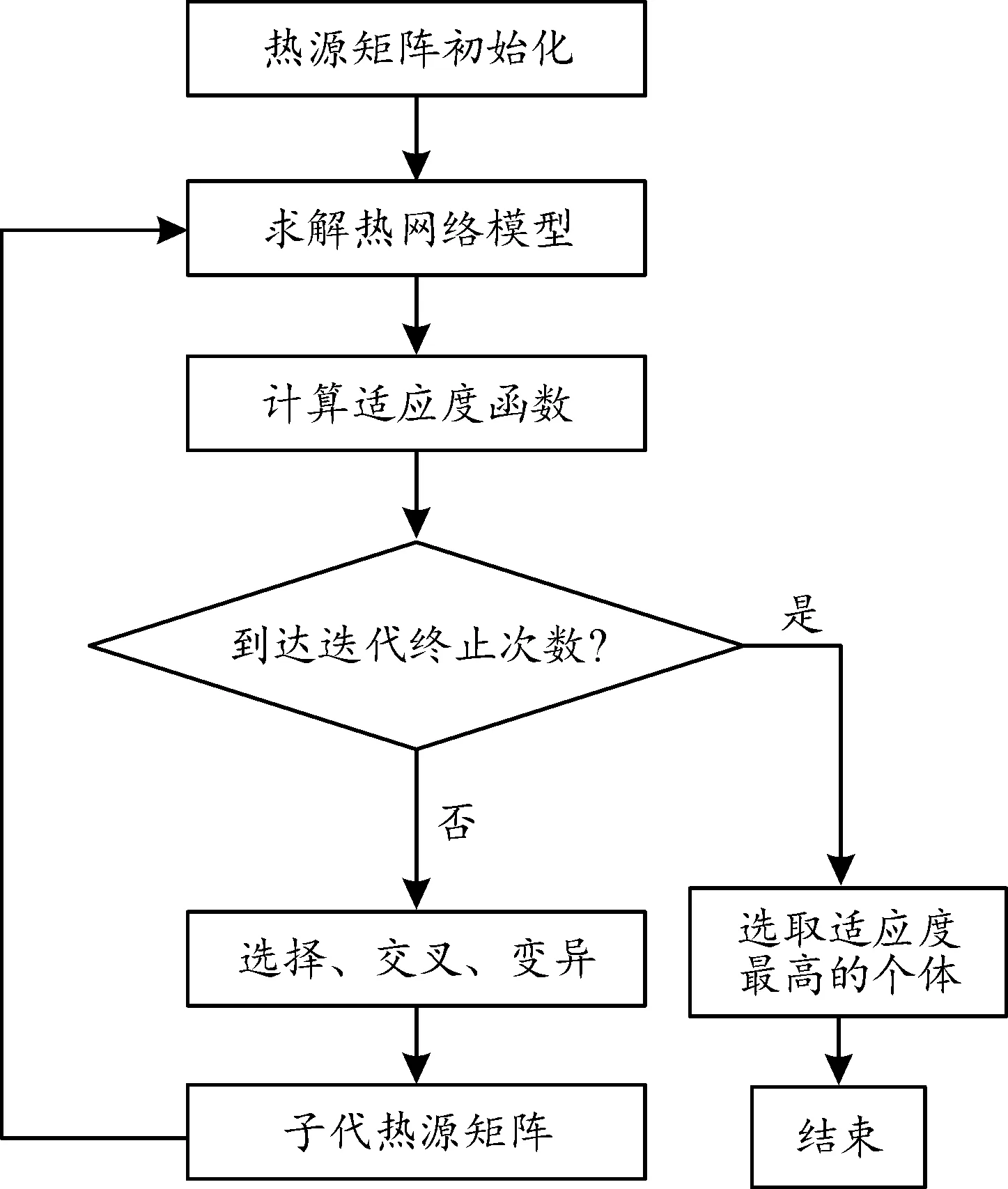
图9 优化流程
3.1 热网络模型
为了提高优化效率,对主板温度分布的求解不再沿用前文的全域求解方式,而是根据主板在控制器内部的传热情况,建立了板级热网络模型。将主板和板上元件离散为图10所示的均匀网格单元,所有网格的长宽均为2.24 mm,电路板网格高度取板厚1.982 mm,元件网格高度为元件高度。

图10 热网络模型网格示意图
考虑到热传导是决定主板温度分布均匀性的主要传热方式,因此忽略了对流和辐射换热,网格节点之间通过热平衡方程建立联系,即:
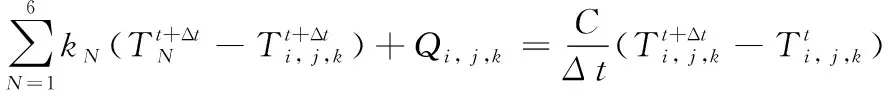
(1)
式(1)中:k为节点间的热导;N为中心节点周围6个节点的坐标;T为节点温度;t为时间;Δt为时间步长;i、j、k为中心节点的坐标;Q为热源;C为网格单元的热容。将所有节点的热平衡方程联立为热平衡方程组,使用高斯-赛戴尔迭代法对方程组进行求解即可得到主板的温度分布。
3.2 遗传算法
将加热膜几何形状优化问题处理为一种节点布置问题(node placement problem,NPP),即在某网格节点布置加热膜则标记为1,不布置加热膜则标记为0。节点布置问题在风力发电、无线传感器网络、石油天然气等领域已经得到了广泛研究,遗传算法是这类问题最常用的优化方法之一[0-0]。
遗传算法是根据生物进化论和遗传学机理发展而来的一种全局搜索方法,它通过对个体适应度的评估来自主积累搜索空间的知识,并对搜索过程进行自动调整,从而搜寻到问题的最优解。遗传算法最常用的编码形式是二进制编码,基本的遗传算子都是根据二进制的特点来对编码串进行操作,这使得遗传算法在处理二进制优化问题时有天然的优势。
3.2.1编码方式、适应度函数与约束条件
将加热膜布置次序作为编码对象,搜索空间为24×21的二维矩阵,编码长度504位,加热膜布置区域编码为1,未布置区域编码为0。编码中的元素与热源矩阵Q中的元素存在对应关系,一个编码次序对应一个热源矩阵。
优化目标为主板的温度均匀性,适应度函数定义为:
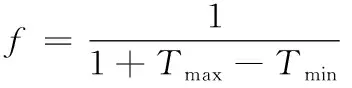
(2)
考虑到实际应用中的限制,将约束条件定为:
1) 加热膜布置区域必须为连通域。若布置区域为非连通域,则需要铺设多张加热膜并分别进行供电,实现过程过于复杂。
2) 加热膜的覆盖面积与原设计保持一致。加热膜形状重新设计以后,板面的元器件也需要重新布局,必须给元器件留下足够的布置空间。
3.2.2操作算子
标准的遗传算法通过选择操作、交叉操作以及变异操作来产生子代,其具体操作策略可以根据优化问题的特点以及约束条件进行改进。各操作算子的执行策略如下:
1) 选择算子采用“轮盘赌”和“最优保留策略”,即每一代中适应度最高的个体完整地复制到下一代,剩余个体采用“轮盘赌”方式选择。
2) 交叉算子执行流程见图11。根据交叉概率选出参与交叉操作的个体作为父辈,为保证交叉后的子代依旧满足连通域约束条件,首先判断配对的父辈是否存在公共点。若不存在公共点则重新进行父代配对;若存在公共点,则随机选择一个公共点作为交叉点执行交叉操作。对交叉后的个体进行连通性判断,若满足连通性,则完成交叉操作;若不满足连通性,则从公共点矩阵中剔除该公共点,并重新选择一个公共点进行交叉,当公共点全部被剔除后依旧无法获得满足连通性的子代,则重新进行父代配对。
3) 变异算子执行流程见图12。经过交叉操作产生的子代只满足连通性约束条件,不一定保证覆盖面积不变,因此通过变异操作来对子代个体进行进一步处理。根据编码中“1”的个数来判定加热膜覆盖面积是否与原设计相等,若大于或小于规定值,则根据差值确定变异基因个数;若等于规定值,则变异的基因个数由设定的变异概率确定。随机选定基因并取反后,若变异子代不满足连通性,则取消取反操作,重新选择其他位的基因进行取反操作,直到子代满足连通性。

图11 交叉流程
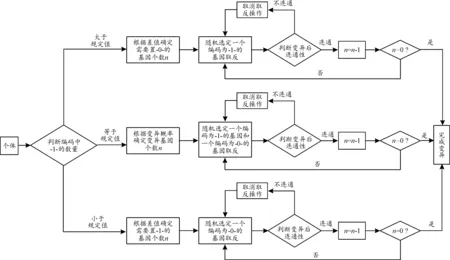
图12 变异流程
3.3 优化结果
设置个体数量为50,交叉概率为0.8,变异概率为0.01,迭代步数为2 000,最优个体适应度随迭代次数的变化如图13所示。优化至第1 100步以后,迭代曲线不再产生明显变化,此时最优个体的适应度值为0.036 8,加热膜的形状如图14所示。可以发现,经过优化后的加热膜在板面分布得更加分散,这有利于热量在电路板水平方向上均匀地扩散。

图13 最优个体适应度值迭代曲线
为验证优化方法的有效性,将重新设计后的主板加热膜代入前文的全域仿真模型进行求解,除主板加热膜形状以外,其他设置保持不变,得到的结果如图15所示。从图15中可以观察到,经过优化后,主板在升温过程中的温度均匀性得到了明显改善,第120 s时,元件的温度范围由原先的-26~+24 ℃缩小至-13~+1 ℃。主板在恒温阶段的温度均匀性也有略微提升,元件的温度范围由原先的-19~-14 ℃缩小至-19~-16 ℃。
优化前后的仿真结果对比表明,优化后的加热膜布局更加合理,加热均匀性更加优异,优化方法是切实有效的。
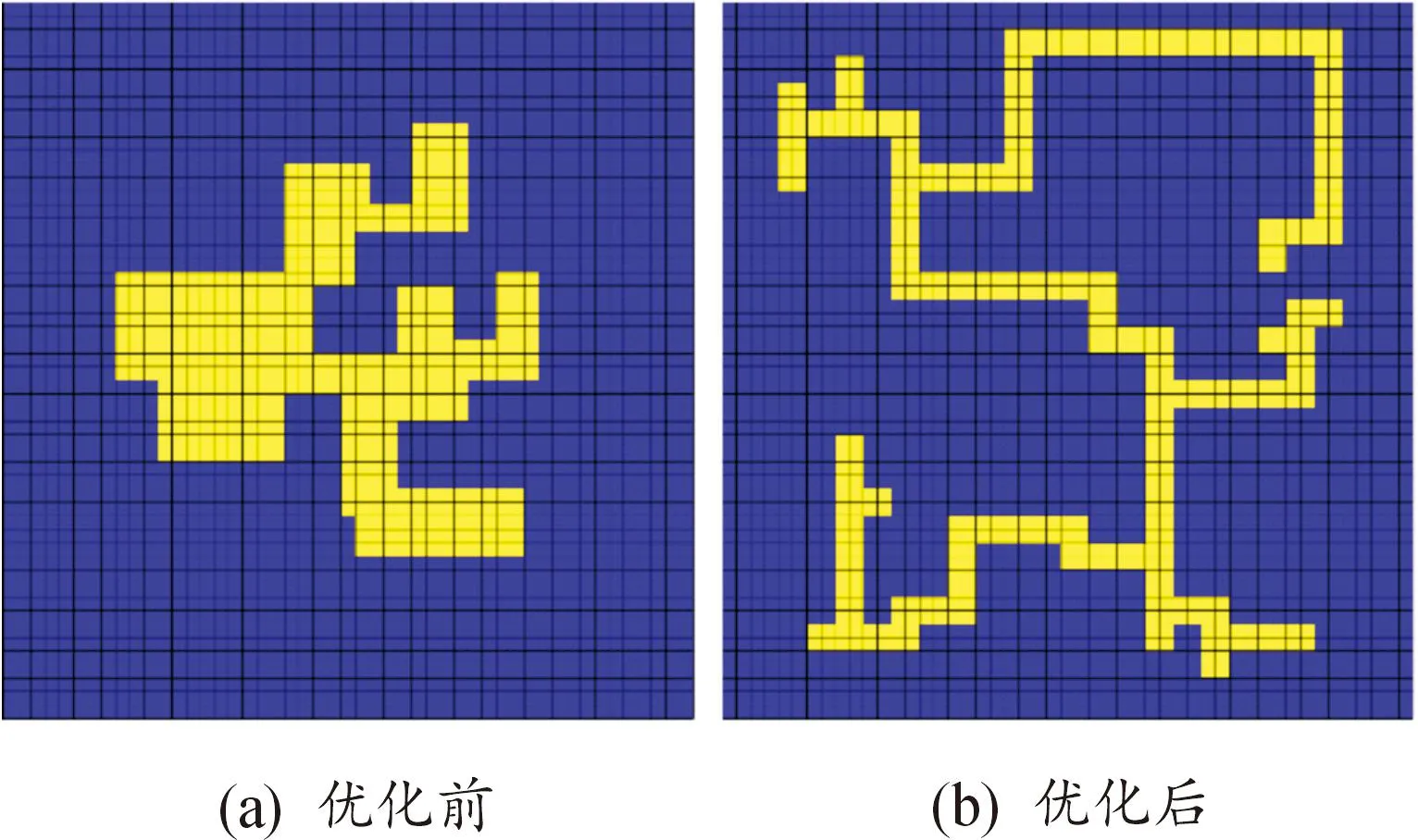
图14 加热膜优化前后对比图

图15 加热膜优化后主板温度分布图
4 结论
本文中以某航空发动机控制器为研究对象,设计了一种基于PI加热膜的加热方案;采用数值仿真和实物实验方法开展了系统级低温加热研究;使用遗传算法对主板加热膜形状进行了优化设计。研究结论如下:
1) 初始设计方案能够满足恒温阶段与升温阶段的温度要求,但是主板元件在升温过程中的温度均匀性较差。环境温度为-55 ℃的情况下:总加热功率10 W,所有元件的稳态温度可以维持在-25 ℃以上;总加热功率70 W,所有元件的温度可以在120 s内提升至-40 ℃以上。
2) 采用遗传算法对主板加热膜几何形状进行优化后,主板元件在升温过程中的温度均匀性有了明显提升。优化前,升温阶段第120 s时主板元件的温度范围为-26 ℃~+24 ℃,优化后,该温度范围缩小至-13 ℃~+1 ℃。对比结果表明,优化后的加热膜布局更加合理,优化方法是有效的。
