GeoGebra用于酸碱滴定曲线精准绘制及滴定终点误差计算

张红医，何珺瑶，石志红,2

1 河北大学化学与材料科学学院，河北 保定 071002

2 河北大学化学教学研究所，河北 保定 071002

酸碱滴定曲线可反映滴定突跃大小和化学计量点，并可指导指示剂选择，是分析化学重要教学内容之一。在分析化学经典教科书中[1]76–81,[2]143–147(中括号后面数字为页码，后同)，滴定曲线绘制通常 以“三段一点”式的方法来完成。滴定前、滴定开始至化学计量点前、化学计量点、化学计量点之后，针对不同阶段采用不同计算式来计算滴定分数所对应的溶液pH，而且只有有限数据点来绘制滴定曲线，这种方法不仅制作过程繁琐而且所绘滴定曲线的精度不高[3]。信息技术为解决这个问题提供了新思路。灵活运用化学平衡关系，可以建立起酸碱滴定曲线的数学模型，获得对滴定过程规律性的认识。此时，滴定曲线的绘制问题则变成了在适当软件辅助下滴定方程的可视化过程，但在实践中还存在如下需要解决的问题：第一，软件版权的制约。已有文献使用Origin[3]和Matlab[4,5]绘制滴定曲线，但这些软件价格不菲，购买这样的软件会在一定程度上增加学生的经济负担，因此限制了它们在课程学习中的应用。第二，已报道的方法操作还不够便捷。不少滴定方程是隐函数，难以写成y=f(x)这种显函数形式，绘制滴定曲线时还需要采取一些巧妙的反函数变换方法[3–6]，将x与y互换后再进行坐标轴的旋转，这些操作增加了滴定曲线绘制的难度。另外当用Origin绘制滴定曲线时偶尔也会在所需滴定曲线之外的边界区域产生奇异曲线。第三，滴定曲线应用不足。在通行的分析化学教材中，滴定曲线绘制与滴定终点误差计算之间缺乏有机衔接，滴定误差计算完全依据基于浓度定义的公式来完成[7]，这不仅阻断了与相对误差概念一脉相承的根本联系，而且也割裂了与滴定曲线的内在逻辑联系，从而影响学生对酸碱滴定问题的全面性和完整性认识。

GeoGebra是一款免费的数学软件，既可在手机上使用，也可在电脑上运行。GeoGebra软件在教学中的应用越来越广泛[8]，但它在化学中的应用还鲜有报道。本文介绍一种新方法将滴定方程推导–滴定曲线绘制–滴定误差计算三者紧密联系在一起，不仅可以帮助学生形成关于酸碱滴定的整体性认识，还会帮助学生在面对酸碱滴定多样化的问题时形成富有共性的处理方法。以电荷平衡关系式和形态分布系数为基础，形成了滴定方程的“三步模型法”。借助GeoGebra为信息化手段，迅速实现基于滴定方程的滴定曲线的精确绘制和滴定终点误差的计算。

1 酸碱滴定方程

酸碱滴定方程就是滴定过程中被滴定溶液pH与滴定剂加入体积(或滴定分数)间的依存函数关系，是软件法绘制滴定曲线的数学基础。下面以两个例子说明“三步模型法”滴定方程的推导过程。

1.1 一元强酸滴定方程——以HCl为例

以NaOH滴定HCl为例，若滴定剂NaOH的浓度为1c，滴定剂的消耗体积为tV，HCl 的初始浓度为c0和初始体积为V0，那么滴定分数则可定义为：。为了使讨论简化，在下面的讨论中沿用通行教材的做法设定c0=c1。一般可以通过以下三个步骤，推导出酸碱滴定方程。

第一步，写出电荷平衡表达式：

第二步，对(1)式中H+和OH−之外各项借助稀释效应(及形态分布系数)进行改写：

将滴定分数的定义代入到(2)中，则有

第三步，考虑到一般滴定曲线都是以滴定分数为横坐标，pH为纵坐标，所以设 [H+] = 10-pH=10-y和[OH-] = 10-14+y代入到(3)式：

1.2 一元弱酸滴定方程——以HAc为例

以NaOH滴定HB为例，滴定剂NaOH的浓度为1c，滴定剂的消耗体积为tV，被滴物HB的初始浓度为0c和初始体积为0V。将前述的滴定方程的三步模型法经验，应用推广到一元弱酸，在问题迁移的过程中，使学生模型化处理滴定方程的能力得到进一步提高。

第一步，电荷平衡关系式。

第二步，非H+和OH−项的形式变换，此时对[B−]变换需要引入形态分布系数。

第三步，将H+和OH−项换为pH表达。

1.3 一元弱碱滴定方程——以NH3为例

以HCl 滴定NH3为例，滴定剂HCl的浓度为c1，滴定剂的消耗体积为Vt，被滴物NH3的初始浓度为c0和初始体积为V0。

第一步，电荷平衡关系式。 [H+] + [NH+4] = [Cl-] + [OH-] (9)

第二步，非H+和OH−项的形式变换，需要引入形态分布系数对 [NH+4]进行变换。

第三步，将H+和OH−项换为pH表达。

1.4 多元碱的滴定方程——以Na2CO3

以HCl滴定Na2CO3为例，滴定剂HCl的浓度为c1，滴定剂的消耗体积为Vt，Na2CO3的初始浓度为c0和初始体积为V0。按照前述的三步模型法推导过程进行滴定方程的推导：

第一步，电荷平衡关系式。

第二步，非H+和OH−项的形式变换，需要引入形态分布系数。为了书写方便，定义M为：

则有：

第三步，将H+和OH−项换为pH表达。

1.5 混合体系的滴定方程——以甲醛与铵的混合体系为例

假设最初的铵盐为氯化铵，经过甲醛处理后相当于被滴定的物质 H+和(CH2)6N4H+，按照前述的三步模型推导过程进行滴定方程的推导：

第一步，电荷平衡关系式。

第二步，非H+和OH−项的形式变换，需要引入形态分布系数对 [(CH2)6N4H+]进行变换。为了书写方便，令

第三步，将H+和OH−项换为pH表达。

2 GeoGebra软件滴定曲线的绘制

GeoGebra软件可以在计算机、手机上运行，下面以计算机上的操作为例，说明如何利用它进行滴定曲线的绘制。

首先登录GeoGebra的国内镜像网站(https://ggb123.cn)，然后点击图1中的“计算器套件”进入到GeoGebra的工作界面。可以把工作界面按照功能大致分为三个区(如图2所示)：(1) 最左面的模型录入区；(2) 录入操作键盘区；(3) 图形显示区。

图1 GeoGebra的镜像网站界面

图2 GeoGebra的工作界面

将“酸碱滴定方程”部分所推导出的模型录入到图2的模型录入区后，然后通过对图形显示区右侧的齿轮形调节钮，对图形的横纵坐标最大显示值进行适当调整，最终得到酸碱滴定曲线。与以往的滴定曲线的绘图工具相比，首先，GeoGebra不仅是免费的，而且在电脑和手机上都可以运行。其次，前述的滴定方程很多较难得到显函数形式，但以前报道的软件大都只能根据显函数形式的模型绘制滴定曲线，而GeoGebra软件可以直接根据隐函数形式的模型而画出相应的曲线。再次，在模型输入区将数学模型键入过程中，十分接近化学工作者的自然语言，几乎不需要额外掌握特殊的命令。

下面以一元强酸滴定曲线绘制为例，来说明GeoGebra绘制滴定曲线的操作过程。式(4)为一元强酸的滴定方程，假设被测物的初始浓度c0= 0.1000 mol·L−1。因此首先在图2的模型录入区录入c0= 0.1后，回车；然后在第二行将式(4)录入。此时，在图形显示区可以看到图形了，为了能得到更加直观地显示，点击图形显示区右上角的齿轮状的设置按钮；最后设置x的最小值为0，x的最大值为2，y的最小值为0，y的最大值为14。这样就可以得到滴定曲线的直观显示了。

要是想得到一元强酸浓度分别为0.01、0.1和1 mol·L−1三个不同浓度的滴定曲线，则需将c0= 0.01、0.1和1分别代入到式(4)，然后分三行录入三个方程，调节齿轮状调节按钮后，得到的最终滴定曲线(图3所示)。

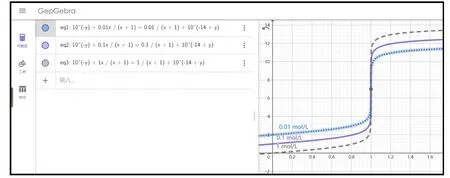
图3 三个不同浓度HCl (0.01、0.1和1 mol∙L−1)的滴定曲线

式(8)和(12)分别为一元弱酸和一元弱碱的滴定方程。选定一元弱酸为HAc (pKa= 4.76，初始浓度为0.1000 mol·L−1)，一元弱碱为NH3(pKb= 4.75，初始浓度为0.1000 mol·L−1)。将这些信息和滴定方程一起输入到GeoGebra，得到滴定曲线如图4所示。

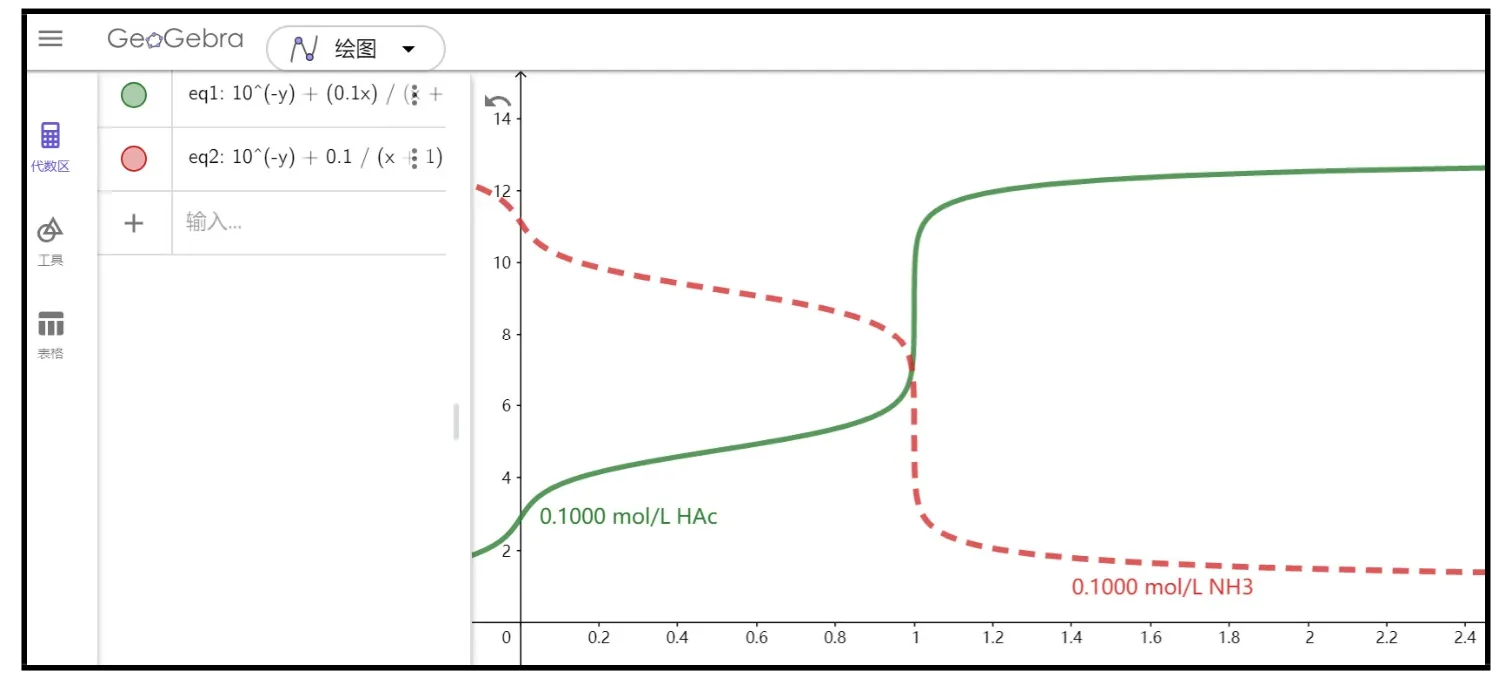
图4 浓度为0.1000 mol∙L−1的HAc和NH3的滴定曲线

按照式(17)绘制多元弱碱的滴定曲线时，操作流程与前面的方法基本一致。Na2CO3(pKa1= 6.38，pKa2= 10.25)的初始浓度设定c0= 0.1000 mol·L−1，它们的滴定曲线如图5所示。按照式(21)可以绘制出NaOH滴定甲醛与铵盐反应后产物的滴定曲线(曲线如图6所示)。

图5 浓度为0.1000 mol∙L−1的Na2CO3的滴定曲线

图6 浓度为经甲醛处理后的0.1000 mol∙L−1 的滴定曲线

3 滴定方程的应用与滴定误差的计算

滴定终点误差的计算是分析化学教学中的一项重要内容。目前分析化学教材大都是依据基于浓度定义的公式来开展终点误差的计算。而运用终点误差的浓度定义式往往需要依据具体的滴定类型而发生变化，从而造成了终点误差公式的碎片化问题[7]。另外，教材中的滴定误差计算过程普遍与滴定曲线之间缺少必要的联系，没有挖掘二者之间的共性，导致学习知识点多，碎片记忆多。本文在三步模型法推理的基础上，将滴定方程-滴定曲线-滴定终点误差有机联系在一起，形成了对滴定分析的共性认知，系统性大大增强，也减少了机械性记忆。采用GeoGebra软件可将滴定方程迅速转化为可视化的滴定曲线。然后再通过命令nsolutions (｛y= pHep，x｝)可迅速得到终点时所对应的滴定分数xep。由于滴定误差就是由于指示剂所指示的终点与化学计量点不一致所产生的误差，其本质就是相对误差(见式22)：

下面以例1–例3来说明滴定误差的求解过程，以例4–例6来说明滴定方程在混合酸(碱)体系中的应用。

【例题1】计算0.1 mol·L−1NaOH滴定0.1 mol·L−1HCl至甲基橙变黄(pH 4.4)和酚酞变红(pH 9.0)的终点误差[1]87,88。

解：前面已经按照三步模型法得到了对应的滴定方程式(4)，在此不再赘述。接下来可以用GeoGebra快速画出对应的滴定曲线。将表1对应内容录入到GeoGebra如图2所示的模型录入区中，然后根据式(22)得到下面的结果。

表1 GeoGebra辅助下根据pHep确定xep

结果与文献[1]87,88完全一致。

【例题2】计算0.1 mol·L−1NaOH滴定0.1 mol·L−1HAc至pH 9.0和7.0的终点误差[1]87,88。(pKa= 4.76)

解：前面已经按照三步模型法得到了对应的滴定方程式(8)，在此不再赘述。将表1对应内容录入到GeoGebra如图2所示的模型录入区中，然后根据式(22)得到滴定误差。

结果与文献[1]87,88完全一致。

【例题3】计算0.1 mol·L−1NaOH滴定0.05 mol·L−1H2C2O4至酚酞变色时(pH = 9.0)的终点误差[1]87,88。(H2C2O4的pKa1= 1.25，pKa2= 4.29)

解：按照前述的三步模型推导法，得到如下二元弱酸的滴定方程。将表1对应内容录入到GeoGebra如图2所示的模型录入区中，然后根据式(22)得到滴定误差。滴定方程和滴定误差如下：

结果与文献[1]87,88完全一致。

再举三个滴定混合酸的例子，一方面是为了进一步展示本方法解决问题的能力，另一方面是为了引起大家对复杂表达式键入技巧的重视。当酸碱溶液体系变得较为复杂时，势必导致滴定方程表达式的臃肿，而把这样的表达式键入到GeoGebra同一行中在操作上是不方便的，不仅会影响键入速度，在视觉上也不利于对程序的键入检查，因此一方面要做好酸碱滴定方程中同类项合并，以便得到较为精简和美观的表达式；另一方面要做好课上小组间键入经验技巧交流分享，以便丰富和发展将复杂模型拆解成较短的可分步键入形式的“技巧库”。

【例题4】用0.1000 mol·L−1HCl溶液滴定20.00 mL 0.1000 mol·L−1NaOH。若NaOH溶液中同时含有0.2000 mol·L−1NaAc，计算化学计量点以及化学计量点前后0.1%时的pH；若滴定到pH 7.0，终点误差有多大[1]104？(已知：HAc的pKa= 8.48)

解：电荷平衡： [H+] + [Na+] = [Ac-] + [Cl-] +[OH-]考虑滴定过程中锥形瓶中溶液的稀释作用以及形态分布系数，得：

将上述滴定方程键入到GeoGebra软件，并键入下列命令得到结果。

键入命令：solutions[{eq1,x= 0.999}]，则可求出 pH前0.1%=9.71

键入命令：solutions[{eq1,x= 1.001}]，则可求出 pH 后0.1%=8.05

键入命令：solutions[{eq1,x=1}]，则可求出pHsp=8.88

键入命令：solutions[{eq1,y=7}]，则可求出终点时所对应的滴定分数xep=1.011

然后根据式(22)滴定误差有：

结果与文献[1]104一致。

【例题5】用0.10 mol·L−1HCl滴定0.10 mol·L−1甲胺和0.10 mol·L−1吡啶混合液中的甲胺，已知滴定终点的pH比化学计量点的pH高0.5个单位，计算滴定终点误差[2]154。(已知：吡啶阳离子的pKa= 5.23，甲胺阳离子的pKa= 10.62)

解：电荷平衡： [H+] + [PyH+] + [MAH+] =[Cl-]+[OH-]

令c( HCl) =c1,c( Py) =c( MA) =c2,V(HCl) =Vt,V(Sample) =V0,考虑滴定过程中锥形瓶中溶液的稀释作用以及形态分布系数，得：

将上述滴定方程键入到GeoGebra软件，并键入下列命令得到结果。

键入命令：solutions[{eq1,x=1}]，则可求出pHsp=7.93；

键入命令：solutions[{eq1,y= 8.43}]，则可求出终点时所对应的滴定分数Vep= 0.9942，然后根据式(22)滴定误差有：

文献[2]154结果为−0.57%。

【例题6】用0.1000 mol·L−1NaOH溶液滴定0.1000 mol·L−1盐酸羟胺(NH3+OH⋅Cl−)和0.1000 mol·L−1NH4Cl的混合溶液。求化学计量点时的pHsp以及在化学计量点有百分之几的NH4Cl参加了反应[2]169。(已知：NH3+OH 的pKa= 5.96，NH4+的pKa= 9.26)

考虑滴定过程中锥形瓶中溶液的稀释作用以及形态分布系数，得：

将上述滴定方程键入到GeoGebra软件，并键入下列命令得到结果。

键入命令：solutions[{eq1,x=1}]，则可求出pHsp=7.61

通过形态分布系数NH4Cl的参加反应的百分数：

文献[2]169中化学计量点pH和NH4Cl的参加反应的百分数分别为7.60%和2.2%。

4 教学实施

数字时代下，我们一线教师需要思考和探索分析化学课程的新模式。从2008年我们就开展了将信息技术解引入分析化学课堂用以解决分析化学问题的探索[9]。在教学实践中我们发现，PeakMaster软件只能解决酸碱平衡中的溶液pH计算问题而不具备绘制滴定曲线和计算终点误差的能力；CurTiPot软件也主要局限在酸碱滴定问题的解决，而且由于软件所确定的Vep不够准确的问题进而导致终点误差计算结果存在波动的不足[10]；我们也介绍了一种基于Origin软件的溶液pH计算法[11]，除此而外该软件还可以绘制酸碱滴定曲线，甚至也可以绘制其他滴定曲线，但它在绘图的过程中需要进行反函数变换[12]，因而Origin不能很好满足滴定曲线绘制和终点误差计算的教学要求。我们发现，GeoGebra软件不仅可以完美解决分析化学问题，而且具有软件免费、易得、易学(编程语言非常接近化学工作者熟悉的自然语言)等突出优点。经过多年的教学实践中，逐步形成了“强模型化-融信息化-增可视化-去公式化”的分析化学教学新模式(图7)，本文着重介绍其在酸碱滴定中的应用。教改改到深处是课程，教改要真正在学生身上发生化学反应、真正发生质量跃迁。如图7所示，本文提出的分析化学教学新模式不仅通过信息技术改变了教学内容，而且强化了学生的深度参与。

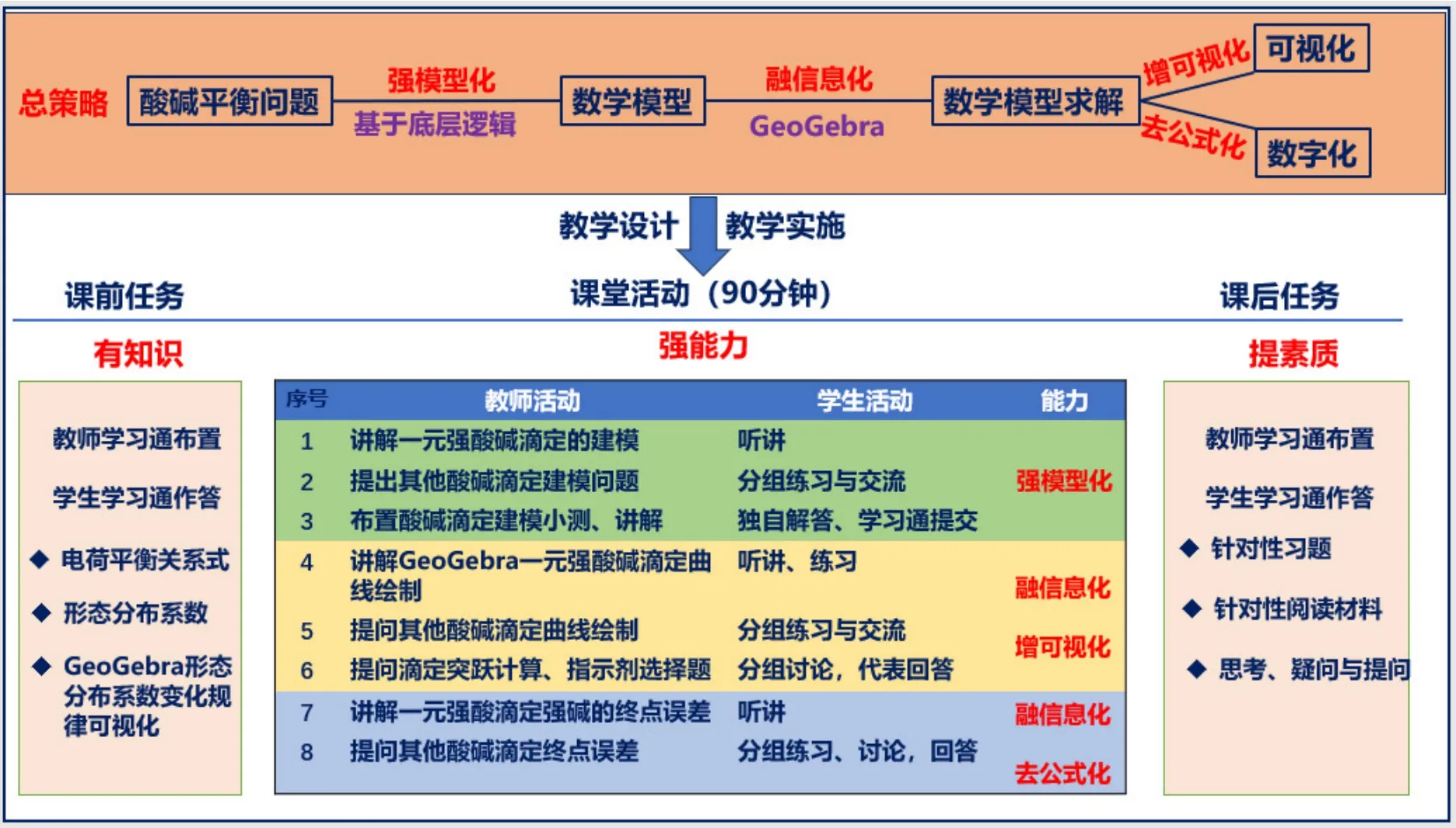
图7 酸碱滴定问题的教学设计

首先，课前要确立预备知识内容，夯实学生学习基础。确立下列内容为本节课的预备知识能力：电荷平衡关系式、形态分布系数的书写和基于GeoGebra的形态分布系数分布规律的可视化；选择和编写针对性的练习题，推送题目到学习通所建班级群，督促学生完成强化课前练习，检验和发现学生课前练习效果。其次，课中开展酸碱滴定模型建立、酸碱滴定曲线绘制和滴定终点误差计算三项逻辑上紧密相连的课堂活动，发展学生解决酸碱滴定问题的能力——“强模型化、融信息化、增可视化和去公式化”。通过对最简单酸碱滴定问题实例的讲授重点阐明解决问题的思路和方法，凸显教师的主导作用；通过对复杂酸碱滴定实例的讨论和练习发展学生解决酸碱滴定问题的能力，凸显学生的主体作用。最后，课后通过针对性的作业和课后阅读材料等任务，激发学生对酸碱滴定产生更深层次的思考，发展学生提出问题能力、自主学习的能力和创新意识。学生学习了本次课以后提出了以下问题：滴定分数可以不为1吗？当滴定分数不为1时，如何确定化学计量点时的滴定分数？通过滴定曲线能否判断可以准确滴定？把化学计量点前后0.1%确定为滴定突跃范围是基于什么考虑？可否用其他值代替0.1%呢？将这些问题梳理后，就产生了下次课程的内容，是对酸碱滴定问题更深入的探讨课程。图7给出了酸碱滴定曲线和终点误差计算的入门阶段内容(2课时)，更高层次的练习和讨论建议额外增加2–4课时。

本部分的教学重点是将酸碱滴定问题转化为酸碱滴定模型。在酸碱滴定模型建立过程中强调分析化学的底层逻辑，这部分内容的底层逻辑就是电荷平衡关系式和形态分布系数，基于底层逻辑所形成了“三步模型法”，删减和弱化了以前的近似式和最简式等内容，不仅保留了此部分分析化学基本内容，还增强了分析化学推理过程的严谨性，避免了机械性记忆的教学内容。之所以将酸碱滴定问题转化为酸碱滴定数学模型确定为教学重点，首先从模型推导过程来看，完全是从分析化学的底层逻辑出发经过严密推理获得的，过程体现了分析化学课程学习的最基本要求；其次从模型的应用来看，它是酸碱滴定曲线绘制和滴定终点误差计算的源头，是利用GeoGebra软件求解的对象。当模型比较复杂时在GeoGebra中如何实现快速录入是教学难点，因为模型键入的正确与否和键入速度很大程度上影响着问题的解决，所以要掌握各种灵活技巧将复杂模型拆解成较短的可分步键入的形式。

如图7所示，通过电荷平衡关系式和形态分布系数将酸碱滴定问题转化为酸碱滴定模型，并经过多年的教学探索发现GeoGebra软件是最适合将酸碱滴定模型转化为可视化曲线和数字解的信息化工具，在此过程中形成“强模型化、融信息化、增可视化和去公式化”的解决酸碱滴定问题的总策略。在此基础上，我们已将这样的思路迁移到络合滴定、氧化还原滴定和沉淀滴定等章节中的滴定曲线和终点误差教学中。针对这些滴定问题的模型建立过程和酸碱滴定模型建立过程存在一定差异，其主要体现在所依赖的分析化学底层逻辑会有不同(比如，络合滴定模型建立中所对应的底层逻辑就是物料平衡关系式和副反应系数)，而在后续的基于GeoGebra软件实现模型的可视化和数字化过程存在明显的相似性。我们已将这种做法应用到整个分析化学课程的化学分析部分，三年多的教学实践表明学生学习分析化学的热情高了，投入多了。

5 教学效果

第一，以电荷平衡和形态分布系数等分析化学基本技能为基础，采用三步模型法得到酸碱滴定方程。推理过程严谨，凸显了共性的推理步骤，夯实了分析化学基本功，易于学生掌握。

第二，GeoGebra软件可以方便地将所建立的酸碱滴定方程以图形化的方式展现出来。该软件免费易得，可在不联网情况下使用，在手机、电脑和平板上均能运行，在解决本文的分析化学问题中，几乎不用学习额外的编程内容。所以我们介绍的方法易于推广。

第三，GeoGebra软件的编程语言最接近化学工作者的自然语言，而且它可以方便地实现将所建立的隐函数滴定模型图形化和数字解。

第四，本文介绍的方法将滴定方程的推导、滴定曲线显示和滴定误差的计算有机结合在一起，解决了目前教材里滴定曲线的绘制与滴定误差的计算存在二者关联性不强的问题，解决了滴定误差计算存在推导复杂、公式类型多的问题。

6 结语

经过多年实践，我们已经形成了“强模型化、融信息化、增可视化、去公式化”的分析化学教学方法，已经连续三年在我校本科教学中使用，涉及学生480余人。相较于以前的教学方法，学生学习热情高了，学习效果好了，相关计算题目正确率由以前的不到50%提升到了近90%。在数字赋能呼声越来越高的今天，将信息技术与分析化学教学深度融合，尝试用信息化手段解决传统分析化学教学问题，已成为分析化学教师需要面对的一种新挑战。课程改革改到痛处是教师，我们分析化学教师不仅要成为信息技术与分析化学教学深度融合的拥趸者和实践者，也应该努力成为引领者。