考虑中频变压器非理想几何结构的通用漏感解析模型

郭 轩，郑泽东，李 驰

（清华大学 电力系统及大型发电设备安全控制与仿真国家重点实验室，北京 100084）

0 引言

变压器漏感定义为只与一次绕组或二次绕组自身交链的，对互感磁通没有贡献的漏磁通所对应的集总参数电感［1］。其通常作为功率传输组件或谐振元件，对变换器的运行特性和效率特性产生较大影响［2⁃3］，因此需要对变压器漏感进行精准建模。

变压器漏感计算通常分为解析法和数值法，数值法指有限元仿真算法，通过求解小区域内麦克斯韦边值问题得到整体问题的解，计算精度高，误差通常在5 % 以下，但计算复杂度高，计算时间长［4⁃5］。而中频变压器优化设计往往需遍历数万乃至数百万个设计点［6⁃7］，漏感数值计算法难以满足设计要求，因而对于漏感计算的研究主要集中于解析建模计算。

变压器漏感解析计算方法通常采取能量法，基于变压器理想几何结构假设，即漏磁场只存在沿窗口高度方向的一维分量，且沿窗口宽度方向漏磁场强度呈线性梯形分布。通过对原边绕组、副边绕组及原副边绕组间绝缘区域漏磁能量积分后便可得到整体漏感［1，8⁃10］。该方法计算简单，且对于理想几何结构变压器漏感的求解计算精度较高。文献［11⁃13］基于以上方法，进一步考虑高频条件趋肤效应和邻近效应对磁场分布的影响，实现了高频条件下理想几何结构变压器漏感的精准建模。但因绝缘要求等原因导致的变压器非理想几何结构（如原副边绕组高度不等，绕组非密绕导致匝间距离对漏磁计算的影响不可忽略）会使得“漏磁场只存在沿窗口高度方向的一维分量”的假设不再成立，因而上述模型在求解非理想几何结构变压器漏感时误差极大［14⁃17］。

目前对于非理想几何结构变压器漏感的解析计算研究集中于基于物理模型和基于数据驱动算法的公式推导。文献［18］提出基于数据驱动算法的漏感求解方法，基于大量仿真数据，拟合复杂多项式的系数，进而通过复杂多项式预测非理想几何结构变压器漏感，实现较高的计算精度，计算误差在10 % 以下。但基于数据驱动算法的漏感求解方法需大量数据（50 000 组及以上）进行训练拟合，拟合复杂度较高，且无明确物理含义，难以适用于所有漏感求解情况。

对于基于物理模型的漏感计算，文献［15⁃16］对于原副边绕组高度相等，但变压器绕组高度小于磁芯窗口高度的简单非理想几何结构，提出一种基于洛氏高度等效的漏感建模方法。在传统理想几何结构下一维漏感模型的基础上引入修正系数。对于简单非理想几何结构求解精度较高，相比传统一维漏感模型，计算误差可由40 % 降至7 % 以下，但该方法对于原副边绕组高度不等、绕组匝间距离不可忽略等更典型的非理想几何结构不适用。文献［19］针对原副边绕组高度不等的非理想几何结构进行基于叠加定理和洛氏高度等效方法的解析建模，相对传统不考虑非理想几何结构的一维漏感模型，计算误差可由50 % 降至7 % 以下。但该模型只针对原边绕组密绕、副边绕组单层绕制的情况。而原副边绕组多层绕制、原副边绕组均为非理想几何结构等更典型、更一般化的非理想几何结构并未被纳入考虑范围。本文在文献［19］的基础上，提出一种更加通用的考虑非理想几何结构的中频变压器漏感解析模型，考虑了原副边绕组多层绕制的非理想几何结构；此外，在原边非密绕情况下，考虑了原边匝间距离对漏磁场分布的影响，旨在进一步提升漏感解析建模的计算精度，为中频变压器优化设计提供理论基础。

1 副边绕组为非理想几何结构的多层绕组变压器漏感建模

非理想几何结构会使变压器部分区域产生漏磁场畸变，进而影响整体漏感的计算，此时变压器漏磁场强不再满足沿窗口宽度方向一维梯形分布的假设，见图1，磁场畸变对漏感解析求解产生较大影响。此外，变压器窗口内外漏磁场分布并不完全相同［17］。图中：|H|为磁场强度模；左、右两图分别对应变压器原副边绕组高度相等及不等的情况。

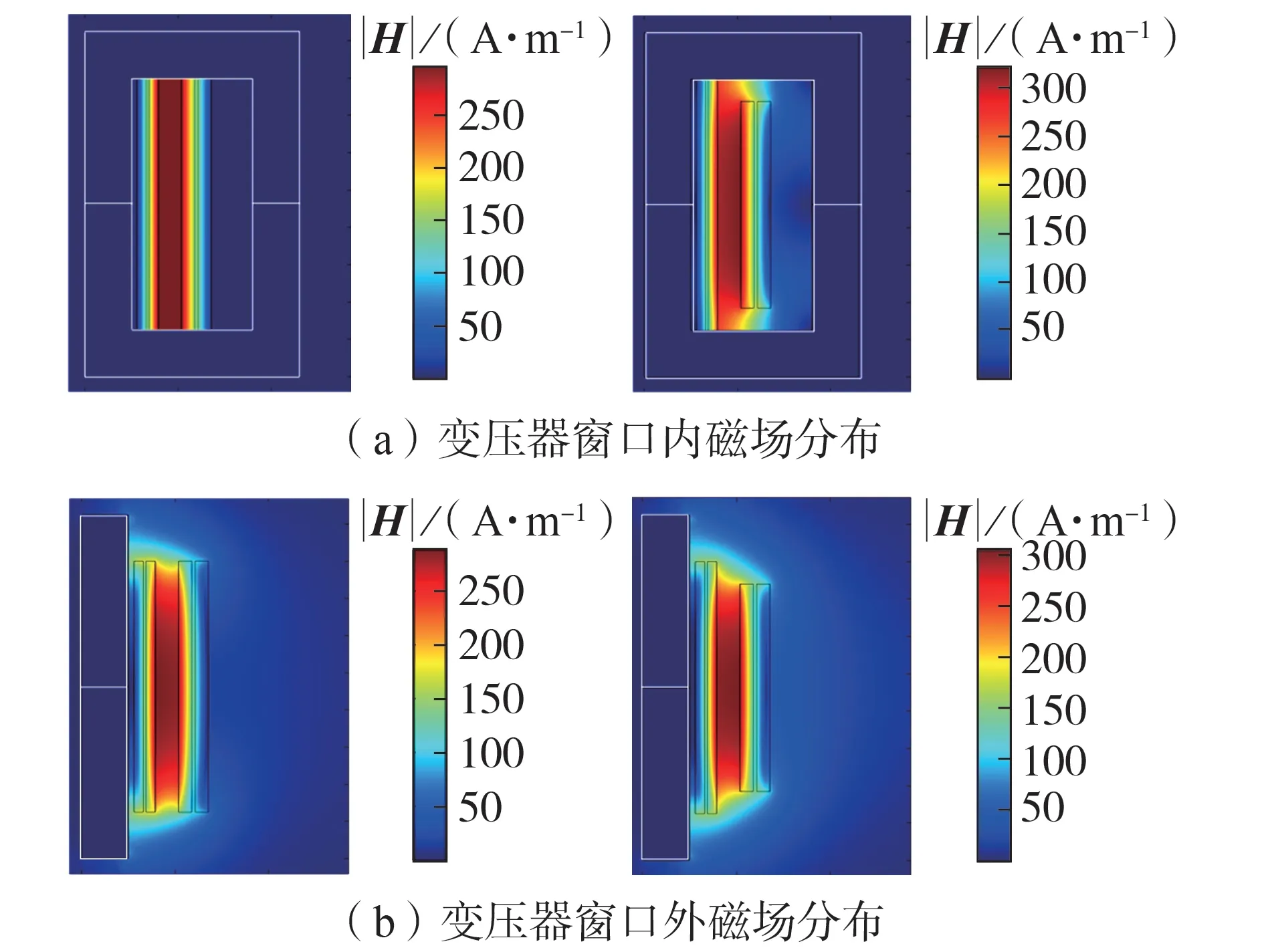
图1 变压器原副边绕组高度相等及不等时漏磁场分布Fig.1 Leakage magnetic field distribution of transformer with equal and unequal winding height of primary-side and secondary-side

因此，需综合考虑非理想几何结构引起的磁场畸变以及变压器窗口内外磁场分布不均的情况。

典型多层绕组变压器排布结构有2 种：第一种为副边多层绕组相同层间（same arrangement，SA）排布，见附录A 图A1（a）；第二种为副边多层绕组优先内层布满（full inter-layer arrangement，FI）排布，首先将内层密绕绕满之后再绕外层，见附录A 图A1（b）。图中：dwp、dws、dins分别为原边绕组宽度、副边绕组宽度、原副边绕组间绝缘距离；hwp、hws分别为原、副边绕组高度；dk1、dk2分别为副边多层绕组相同层间排布、多层绕组优先内层布满排布下原副边绕组高度差的一半；λl为纵向磁场宽度，λl=dwp+dws+dins；s1、s2分别为高度更低的绕组与左侧、右侧磁芯柱的距离。

对于副边多层绕组相同层间排布的结构，原边、副边绕组高度不等，沿窗口宽度方向的安匝数不平衡，此时采用传统Dowell 模型会引起较大误差。对此，本文基于叠加定理将漏磁场分解为安匝数平衡的纵向漏磁场和横向漏磁场的矢量和，如图2 所示。图中：λ1、λ2为2段横向磁场宽度。

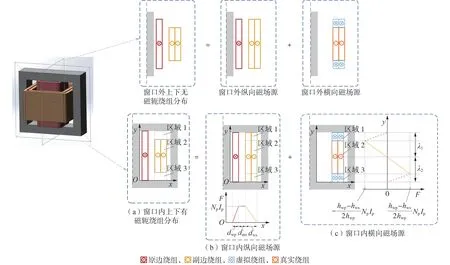
图2 副边多层绕组相同层间排布下漏磁场矢量叠加Fig.2 Vector superposition of leakage magnetic field with same arrangement structure of secondary-side multi-layer winding

图2（a）中原边绕组单位高度磁动势为NpIp/hwp，副边绕组单位高度磁动势为NsIs/hws，且磁动势只存在于区域2中，其中原边绕组磁动势NpIp等于副边绕组磁动势NsIs。首先为保证纵向磁场沿x轴安匝平衡，在图2（b）中将副边绕组延展至与原边绕组相同高度，总磁动势不变，此时区域1 — 3 中副边绕组单位高度磁动势为NpIp/hwp，进一步地，为了保证分解后的磁动势分布与图2（b）中磁动势分布相同，引入虚拟绕组，在图2（c）中令区域1、3的单位高度磁动势为-NpIp/hwp，令区域2 中的单位高度磁动势为NsIs/hws-NpIp/hwp，图2（b）和图2（c）叠加后，仍可保证区域1 和区域3 的单位高度磁动势为0，区域2 中单位高度磁动势为NsIs/hws。此时图2（b）中磁场沿x轴安匝平衡，磁场强度只有y轴分量，图2（c）中磁场沿y轴安匝平衡，磁场强度只有x轴分量。

由于图2（b）中的纵向漏磁场与图2（c）中的横向漏磁场正交，可以分别计算两部分漏磁场能量后标量叠加，以得到整体漏磁场能量。纵向漏磁场和横向漏磁场磁动势分布曲线如图2 所示，由于合适的利兹线线径选取，交流效应对漏磁场分布的影响可以忽略，因此纵向磁场磁动势分布为梯形分布，横向磁场磁动势分布曲线为三角分布。

对于绕组高度小于窗口高度的非理想几何结构，需要采用洛氏高度等效的方法，将不同路径的磁力线转换为全部平行于磁芯窗口高度方向的磁力线，并且各磁力线具有相同的计算高度heq［20］，如图3所示。图中：hw为绕组高度；dw为绕组宽度；deq为绕组洛氏等效宽度。洛氏高度等效方法此前已被Mogorovic 用于纵向漏磁能量计算，但未考虑横向漏磁和窗口内外磁场分布不同的影响［13］。

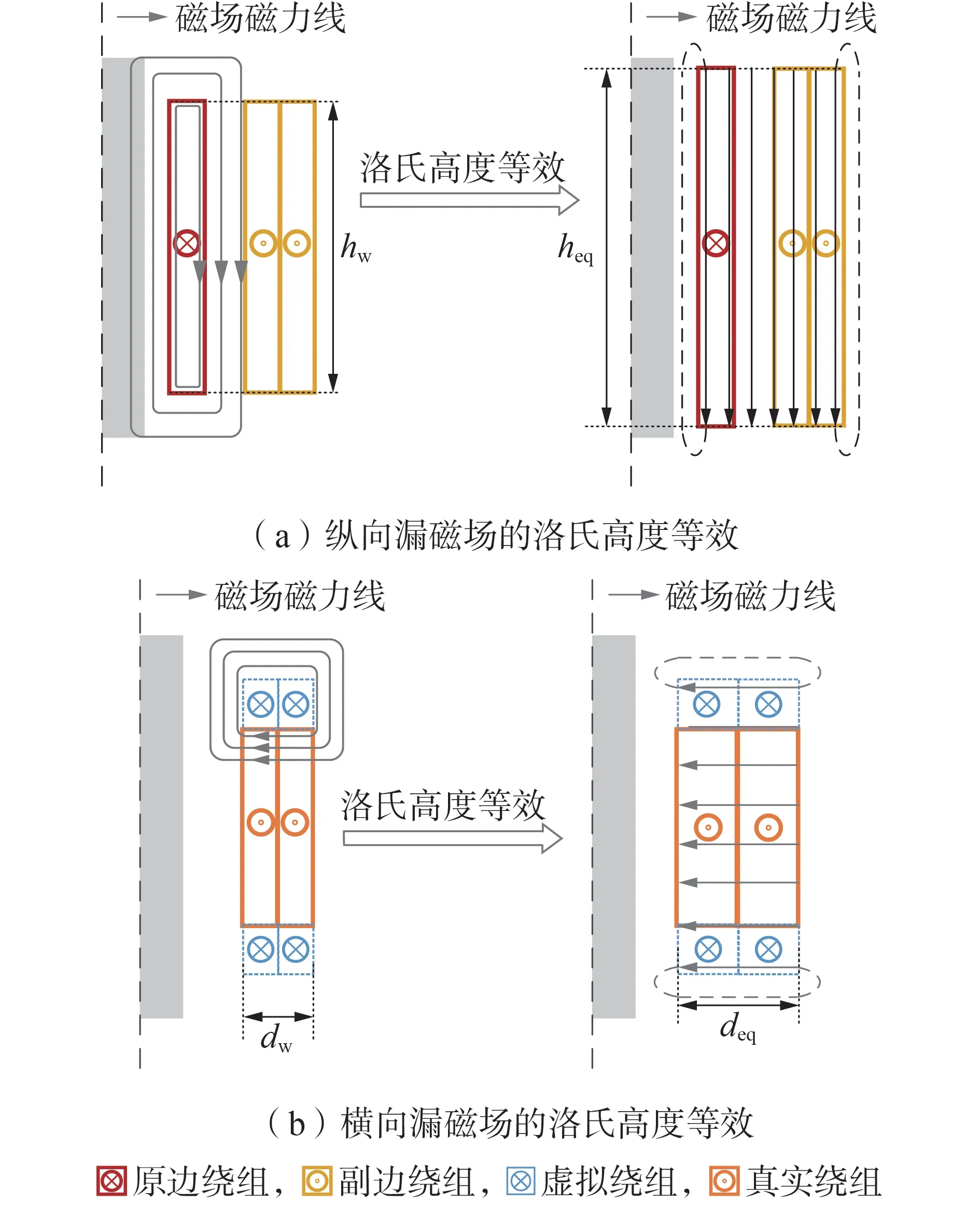
图3 洛氏高度等效示意图Fig.3 Equivalent diagram of Rogowski height

窗口内外漏磁场能量分别计算的思路源于文献［17］，但所提模型为半解析数值模型，非解析模型。

本文解析模型对于窗口内外磁场计算方法相似，窗口内纵向漏磁场能量Wσ，l，IW，pu和窗口外纵向漏磁场能量Wσ，l，OW，pu的计算公式为：

式中：μ0为真空磁导率；heq，l，IW为窗口内洛氏等效高度；ρl为纵向洛氏系数，见附录A 式（A1）；h为窗口高度。式（1）和式（3）的区别主要在于等效的计算磁场高度不同，式（1）中的计算磁场高度为洛氏高度和窗口高度的较小值，而式（3）中的计算磁场高度直接为洛氏高度hwp/ρl。

窗口内横向漏磁场能量Wσ，t，IW，pu和窗口外横向漏磁场能量Wσ，t，OW，pu的计算公式分别为：

式中：λi为第i个区间（横向磁动势两零点之间为一个区间）磁动势曲线中相邻两零点间的距离；Fi为第i个区间的磁动势最大值；n为区间数；ρt，IW、ρt，OW为洛氏系数，分别见附录A 式（A2）、（A3）。式（4）和式（5）的区别主要在于ρt，IW和ρt，OW不同。

整体漏感Lσ主要由Wσ，l，IW，pu、Wσ，t，IW，pu、Wσ，l，OW，pu、Wσ，t，OW，pu构成，计算公式为：

式中：lIW、lOW分别为窗口内、外漏磁场区域的平均长度；I1为激励电流值。传统不考虑非理想几何结构的Dowell 模型正是由于忽略了横向磁场，导致计算非理想几何结构变压器漏感时产生较大误差。

对于副边多层绕组优先内层布满排布结构，副边绕组层间高度不同，沿窗口宽度方向其安匝数不平衡。此结构下，纵向及横向磁场磁动势分布曲线如附录A 图A2所示。对于纵向漏磁场能量计算，其磁动势分布曲线仍然是线性分布，但不再是梯形分布。对于横向漏磁场，只需考虑最外层绕组区域产生的漏磁场能量。多层绕组优先内层布满排布下的纵向漏磁场能量计算公式为：

式中：Ns-in、Ns-out分别为副边绕组内、外层匝数。式（8）、（9）相较于式（1）、（3）的主要区别在于副边绕组区域的磁场能量需分段计算。

多层绕组优先内层布满排布下的横向漏磁场能量计算公式仍如式（4）、（5）所示，但其中Fi为：

文献［19］给出了一种使得非理想几何结构下变压器漏感最小的优化排布方案，即当副边绕组各匝间距离相等，且副边绕组距磁芯顶部和底部的距离为匝间距离的一半时漏感最小。但文献［19］并没有针对多层绕组变压器展开进一步讨论。

对于附录A 图A1 所示的多层绕组变压器，其使漏感最小的最优排布结构如附录A 图A3 所示。相较于图2 和图A2 所示的集中绕组排布，主要区别在于横向磁场磁动势，副边绕组相同层间结构的优化排布下横向磁场磁动势Fi如式（11）所示，副边多层绕组优先内层布满结构的优化排布的横向磁场磁动势Fi如式（12）所示。可以数值证明，图A3（b）所示绕组排布对应漏磁场能量小于图A3（a）所示绕组排布对应漏磁场能量。

2 原副边绕组均为非理想几何结构的变压器漏感建模

本文所建立的模型假设变压器原边绕组密绕，即原边绕组匝间距离可以忽略。但在变压器实际绕制过程中，原边绕组高度通常小于变压器窗口高度，使得原边绕组匝间距离不可忽略。此时，变压器漏感计算需要考虑原边绕组处产生的横向漏磁场能量。叠加定理视角下的纵向磁场与横向磁场分解如图4 所示。横向漏磁场能量由原副边绕组处等效的虚拟绕组共同产生。

原边绕组区域产生的横向磁场Hxp和副边绕组区域产生的横向磁场Hxs与整体纵向磁场Hy正交，而Hxp与Hxs方向相同或者相差180°。此结构下漏磁场能量密度W的计算公式如式（13）所示，式中HxpHxs项只存在于图4所示阴影区域处，该区域被定义为洛氏磁场叠加区域。该区域等效磁场计算高度heq⁃cross如式（14）所示。洛氏区域左侧有Hxs=0，右侧有Hxp=0，当原边、副边磁场区域产生的横向磁场方向相同时HxpHxs项取正，否则该项取负。

式中：ρt⁃ip和ρt⁃is分别为原、副边第i个区间对应的横向洛氏系数。

因此，对于原边匝间距离不可忽略的情况，可以对整体纵向漏磁场能量Wσ，l、原边绕组区域横向漏磁场能量Wσ，t，p、副边绕组区域横向漏磁场能量Wσ，t，s以及如式（15）所示的洛氏磁场叠加区域漏磁场能量Wcross分别计算后进行标量叠加以得到整体漏感值。Wσ，l、Wσ，t，p、Wσ，t，s仍可以由第1 章给出的计算纵向漏磁场能量和横向漏磁场能量的方法计算得到，区别仅在于横向漏磁场磁动势分布不同。最终漏感值由式（16）给出，相比式（7），额外考虑了原边绕组横向磁场能量以及洛氏磁场叠加区域漏磁场能量。

式中：V为体积。

结合图4 和式（16）分析可知：Wσ，l，IW为窗口内纵向磁场能量，对应图4（a）；Wσ，t，p，IW、Wσ，t，s，IW和Wσ，cross，IW分别为窗口内原边区域横向漏磁场能量、副边区域横向漏磁场能量和洛氏叠加区域漏磁场能量，对应图4（b）；Wσ，l，OW为窗口外纵向磁场能量，对应图4（c）；Wσ，t，p，OW、Wσ，t，s，OW和Wσ，cross，OW分别为窗口外原边区域横向漏磁场能量、副边区域横向漏磁场能量和洛氏叠加区域漏磁场能量，对应图4（d）。

3 仿真与实验验证

本文基于EE 80／38／20 和EE 186／76／30 型磁芯搭建了多组样机以验证所提模型的准确性。实验测试图如附录B 图B1 所示，样机实物图如附录B图B2、B3所示。具体仿真和实验参数如附录B表B1所示，分号分隔不同磁芯型号下的绕组型号，仿真和实验平台分别基于COMSOL Multiphysics 5.4 和稳科精密阻抗分析仪6500B。

3.1 多层绕组漏感模型验证

图5 和附录C 图C1 分别展示了EE 80／38／20和EE 186／76／30 磁芯样机多层绕组变压器在不同绕组结构（多层绕组相同层间排布结构、优先内层布满结构），不同绝缘距离下，漏感随dk1和dk2变化的曲线以及理论模型的解析值与有限元仿真值之间的误差比较。相较于有限元仿真，理论模型解析值的误差最大值为7.5 %。

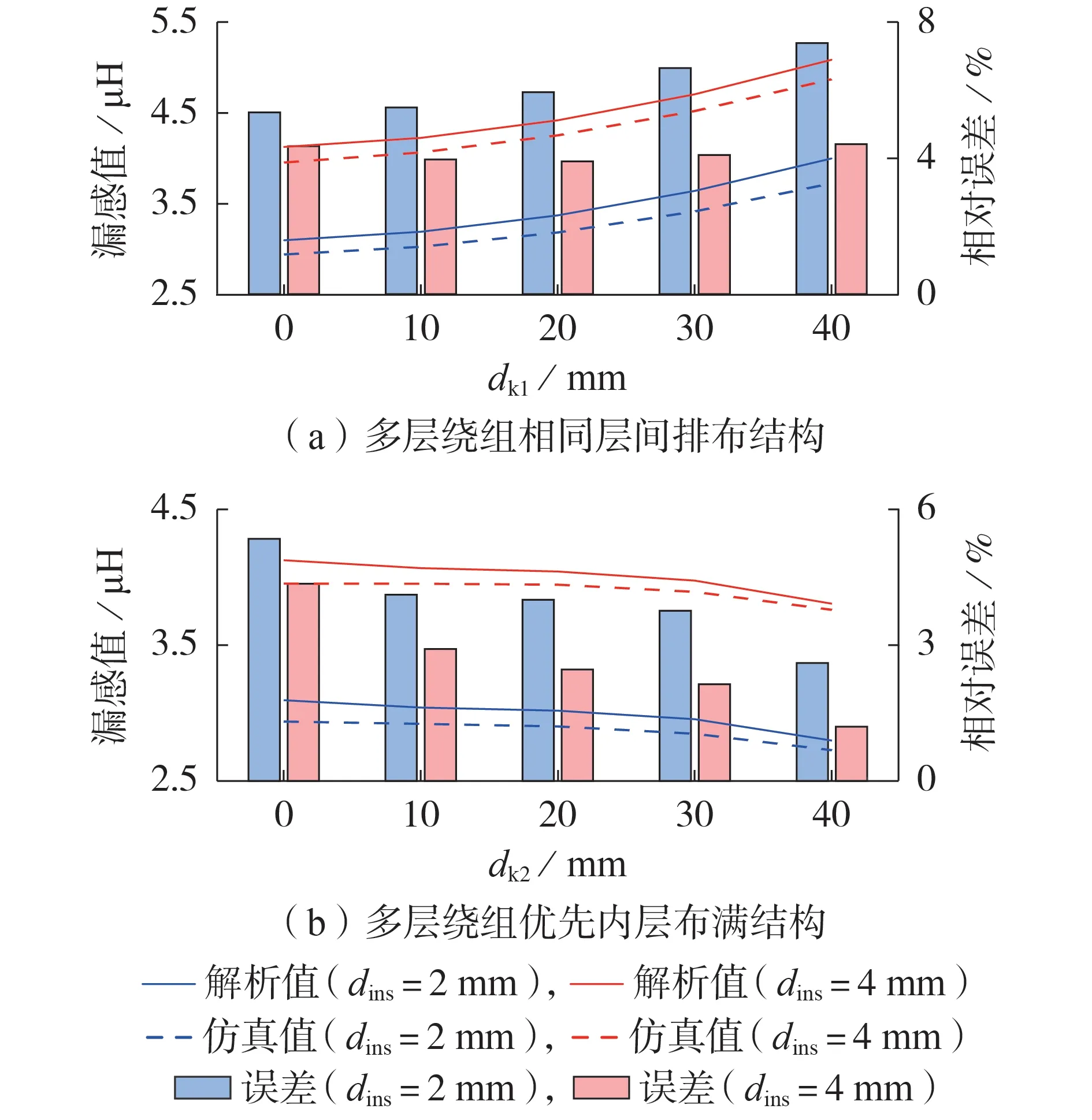
图5 多层绕组变压器漏感随dk1和dk2变化的曲线及误差比较（磁芯型号EE 80／38／20）Fig.5 Curves of leakage inductance of multi-layer winding transformer changing with dk1 and dk2，and error contras（tCore type is EE 80／38／20）

图6给出了EE 80／38／20磁芯样机，在不同绕组结构（多层绕组相同层间排布结构、优先内层布满结构）下，优化排布，漏感随副边绕组匝数Ns变化的曲线（Ns不同，即dk不同）以及理论模型的解析值与有限元仿真值之间的误差比较。相较于有限元仿真，理论模型解析值的误差最大值不超过5 %。

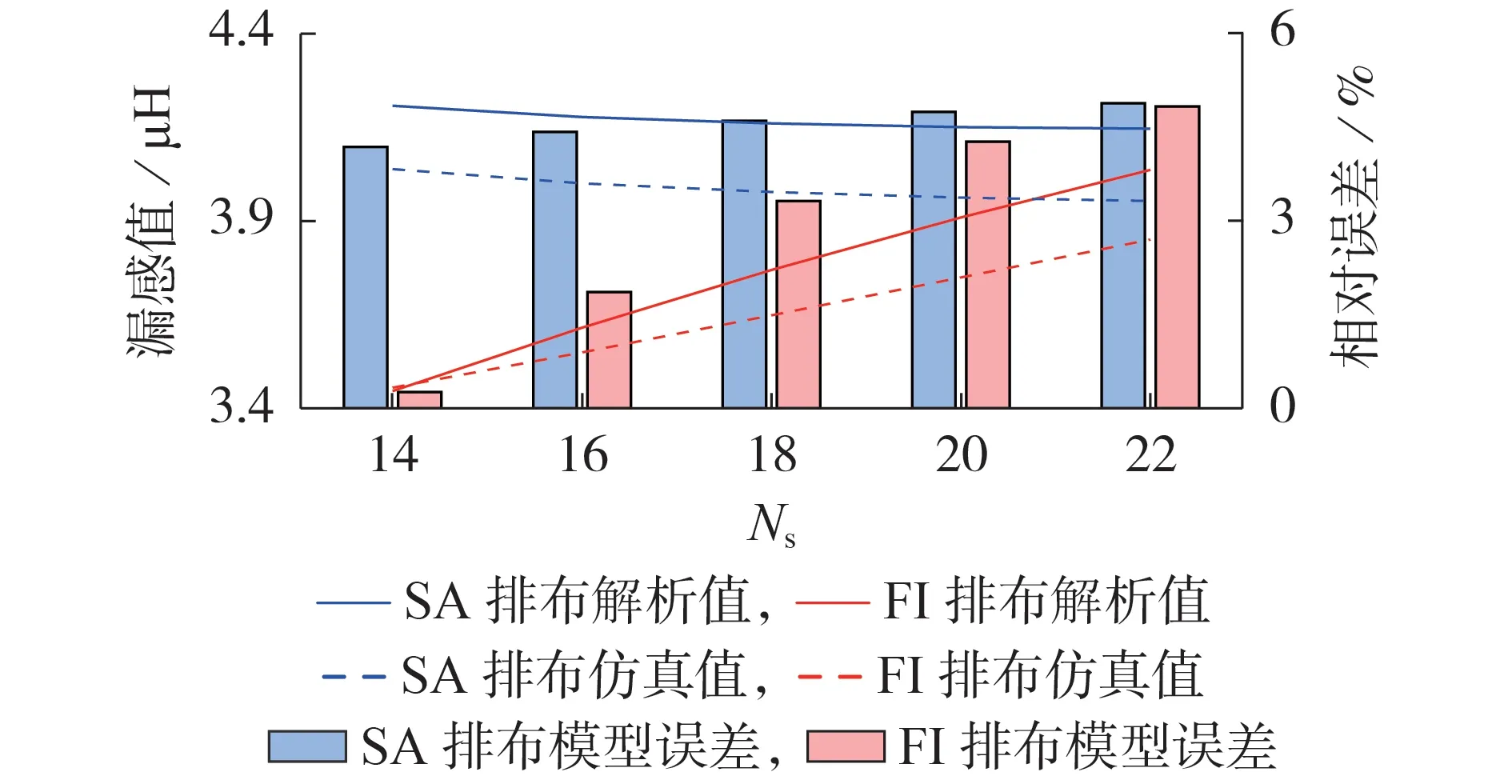
图6 多层绕组变压器漏感随Ns变化的曲线及误差比较（磁芯型号EE 80／38／20，优化排布）Fig.6 Curves of leakage inductance of multi-layer winding transformer changing with Ns，and error contrast（Core type is EE 80／38／20，optimized arrangement）

对于窗口内外漏磁场能量分别进行计算的准确性验证，附录C 图C2 给出了EE 80／38／20 磁芯样机在不同绕组结构（多层绕组相同层间排布结构、优先内层布满结构）下，窗口内外漏磁场能量对应的单位长度漏感随dk1和dk2变化的曲线，及理论模型与有限元仿真值之间的误差比较。相较于有限元仿真，窗口内外理论模型的误差最大值为6.4 %。

对于横向磁场与纵向磁场分解准确性的验证，附录C 图C3 给出了EE 80／38／20 磁芯样机，横向漏磁场能量、纵向漏磁场能量及整体漏磁场能量对应漏感随dk1和dk2变化的曲线，及理论模型与有限元仿真值之间的误差比较。相较于有限元仿真，纵向漏磁场能量和整体漏磁场能量误差在5 % 以下，横向漏磁场能量误差在10 % 以下。

分别对附录B 图B2 所示的样机进行短路实验，测量不同结构、不同绕组排布下的漏感，结果如表1所示。由表可知，最大实验误差为6.5 %，本文所提模型有较高的计算精度。此外，相较于典型的多层绕组集中排布，优化排布下的漏感值可减小31 %。

表1 多层绕组变压器样机漏感实验测量结果Table 1 Experimental results of leakage inductance of multi-layer winding transformer prototype

3.2 原副边绕组均为非理想几何结构下漏感模型验证

图7 和附录C 图C4 分别展示了EE 80／38／20和EE 186／76／30 磁芯绕制的变压器，在原边绕组非密绕结构下，变压器样机漏感随dins和Ns变化的曲线。相较于Dowell 模型（计算误差在50 % 以上）和文献［19］中未考虑洛氏磁场叠加区域的模型（计算误差为15 %），本文所提模型的计算误差可降至4 %。

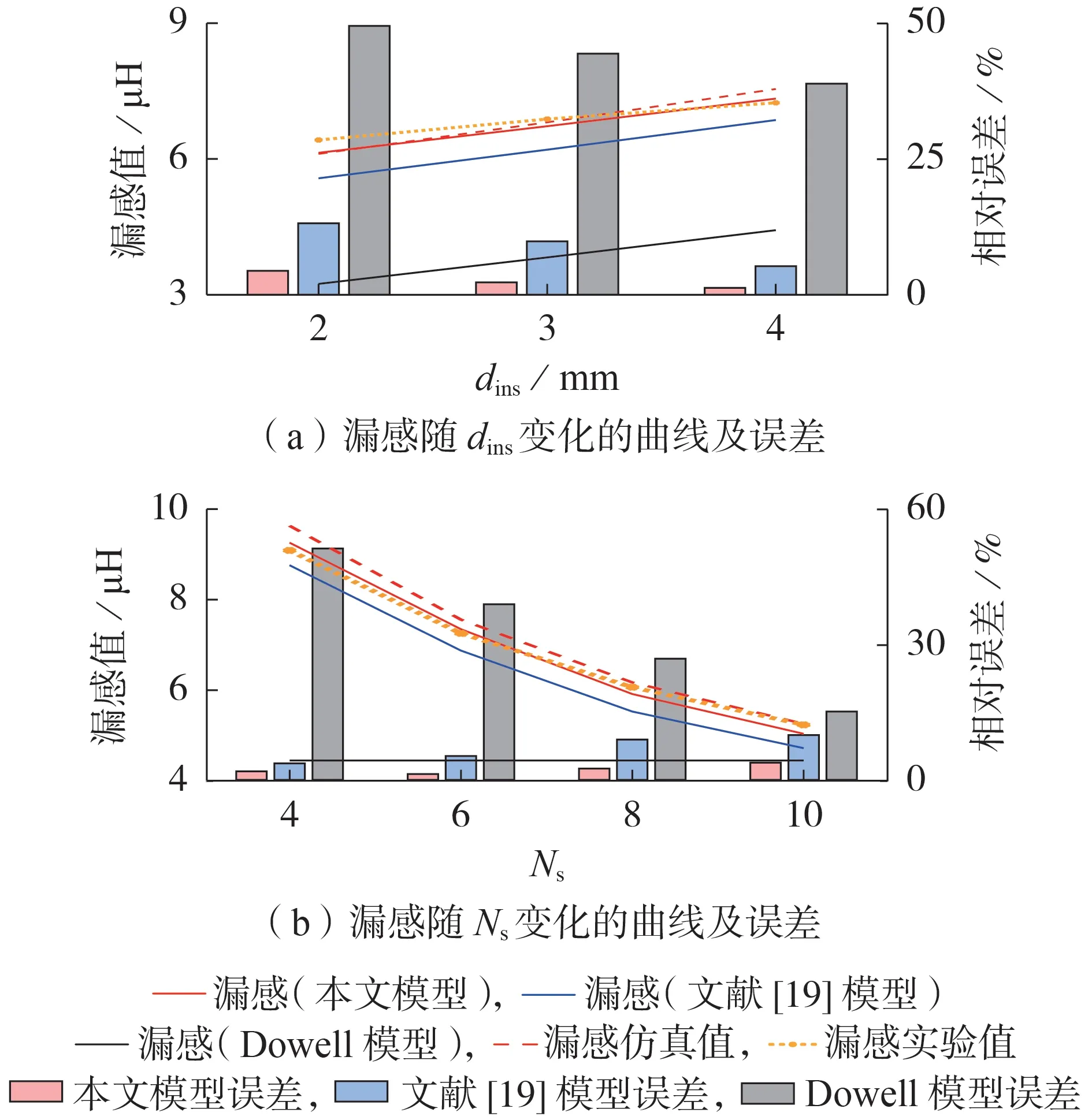
图7 原边非密绕结构变压器漏感随dins及Ns变化的曲线及误差比较（磁芯型号EE 80／38／20）Fig.7 Curves of leakage inductance of transformer considering turns distance in primary-side changing with dins and Ns，and error contrast（Core type is EE 80／38／20）

本文所提模型的误差来源一部分在于将绕组区域磁动势视为线性分布，忽略了高频效应对磁场分布的影响，虽然可通过合适的利兹线线径选取来抑制高频效应，但仍会造成一定误差；另一部分在于洛氏高度等效方法是将不同路径的磁力线转换为全部平行于磁芯窗口高度方向的磁力线，并且各磁力线具有相同的计算高度，可极大地降低计算复杂度，但不具备底层物理意义，等效过程中也会造成一定误差。此外，实验测试过程中绕组匝间距离很难被精确控制，也会造成一定的测量误差。

4 结论

本文针对基于EE 型磁芯及利兹线绕组的壳式结构变压器，在保证适用频率使得利兹线单股线径小于趋肤深度的基础上，基于叠加定理和洛氏高度等效方法计及了变压器实际绕制过程中的典型非理想几何结构对漏感计算精度的影响，提出一种通用的高精度漏感解析模型。

首先针对副边绕组为非理想几何结构的多层绕组变压器的典型绕组形式（副边绕组层间排布相同和优先内层布满排布），一方面修正了纵向漏磁场磁动势分布曲线，另一方面考虑了横向漏磁场能量的影响，将一维磁场计算模型改进为二维磁场计算模型。在此模型的基础上，通过改变副边绕组排布实现了最小漏感的优化排布。

进一步，针对原副边绕组均为非理想几何结构的变压器，在考虑副边横向漏磁场能量的基础上，考虑原边横向漏磁场能量以及洛氏叠加区域的原副边绕组耦合横向漏磁场能量，将漏感模型完善为全面的二维多区域磁场计算模型。

本文所提漏感解析模型，一方面显著提升了计算精度，另一方面相较于有限元计算，即使是二维有限元，计算效率也可提升5 个数量级。研究工作可以为中频变压器优化设计提供理论模型基础，同时为中频变压器漏感调整提供了除调整绕组匝数及绝缘距离以外的新方法。

附录见本刊网络版（http：//www.epae.cn）。