配电网的最小供电能力：定义、模型、求解和应用

肖 峻，蔡仲伟

（天津大学 智能电网教育部重点实验室，天津 300072）

0 引言

配电网是电力系统的一个重要环节，其主要作用是保证对用户的可靠持续供电。供电能力是衡量配电网建设水平的主要指标［1］，在配电网规划和评估中经常被使用。文献［2］借鉴最大输电能力（to⁃tal transfer capability，TTC），提出最大供电能力（to⁃tal supply capability，TSC）的名称，将其定义为某供电区域内配电网满足一定安全准则（通常是N-1 准则）的最大负荷供应能力［2］。

现有关于TSC 的研究涉及数学模型［3⁃5］、求解方法［6⁃7］、规划应用［8］、调度运行应用［9］等。在TSC 的启发下，有学者提出以剩余供电能力衡量在不削减已有负荷的前提下配电网的可用供电潜力［10］。进一步，有学者将其应用于考虑荷储动态特性的有源配电网中［11］。

“TSC”中的“T”表示“total”，指“全网所有的”，并非“最大的”，但由于在早期的研究中配电网的供电能力是一个值，因此，关于“最大供电能力”的译名无太大争议。而在后续研究中，文献［12］发现配电网的供电能力不是一个值，而是一个范围，该范围可采用TSC 曲线进行描述，原TSC 是该曲线上的最大值，用“total supply capability”表示其英文全称不再合适，因此，本文将原TSC 的英文全称修改为“maximum total supply capability”，记为TSCmax。TSC 曲线完整描述了配电网在各种不同系统状态下的带负载能力。文献［13］提出TSC 曲线的数学模型，并揭示其形成机理。TSC 曲线的最高点TSCmax是评估配电网的一个重要指标。

TSC 曲线的最低点称为最小供电能力（mini⁃mum total supply capability，TSCmin）［14］。TSCmax对应配电网安全运行中效率最高的临界负载状态，TSCmin对应配电网安全运行中效率最低的临界负载状态，可见，TSCmin是TSCmax的对偶指标。近十年来，TSCmax已得到了大量的研究，而关于TSCmin的研究尚处于空白状态。本文首次对TSCmin开展基础性研究，提出TSCmin的定义、数学模型和求解方法。TSCmin的研究成果不仅是供电能力理论的一个重要补充，而且具有实际工程意义：得到TSCmin对应的系统状态后，调度人员可以引导工作点规避TSCmin点，即避免系统陷入供电能力值最低但又处于临界安全的最不利状态。本文给出规避TSCmin点的预测控制方法，结合负荷预测，提前采取规避措施干预工作点的发展趋势，避免系统的N-1安全性遭到破坏。

1 安全边界相关定义及交叉机理简介

1.1 安全边界相关定义

配电网的安全边界点可根据是否满足严格临界性［15］分为严格安全边界点和非严格安全边界点，分别简称为严格边界点和非严格边界点。严格边界点具有严格临界性，即任何一个负荷单独增加均一定造成不安全。严格边界点的数学描述［16］为：若工作点W=[L1，L2，…，Ln]（Li(i=1，2，…，n)为第i回馈线上的负荷，n为馈线回数）位于安全边界βse上，即W∈βse，则第i回馈线上的负荷增加后形成新的工作点W'=[L1，…，Li+ε，…，Ln]（ε为任意小的正数），如果对于∀ε＞0 和i∈{1，2，…，n}均有W'∉βse，则称W为严格边界点。

严格边界是所有严格边界点构成的集合，记为βst。实际配电网完整的严格边界一般由多个独立严格边界（后文简称独立边界）组成，每个独立边界均具有唯一确定的表达式。将βst中的第j个独立边界记为βj。严格边界的表达式是在配电网安全域（distribution system security region，DSSR）表达式［16］的基础上，将部分不等式变为等式得到的，等式覆盖全部负荷变量，从而保证严格临界性。

1.2 交叉机理简介

在安全边界等式约束中多次出现的变量称为交叉量［13］。将一个独立边界所有等式约束的等号两侧分别求和得到的等式称为等式约束和式［13］。边界βj上等式约束和式的标准形式为：

式中：Ltotal(W)为严格边界点W的总负荷；Rj为冗余式［13］，冗余式的取值是冗余量，其最小值和最大值分别为最小冗余Rminj和最大冗余Rmaxj；Csum为容量和常数。

交叉机理中与本文TSCmin相关的内容如下：

1）若严格边界等式约束中存在交叉量，则会导致等式约束和式中出现冗余式；

2）最大冗余时，配电网处于最不利的备用状态，N-1 故障后联络馈线将出现最大的容量浪费，此时工作点总负荷Ltotal(W)达到最小值TSCmin。

2 TSCmin

2.1 TSCmin的定义

TSCmin的定义为：配电网满足严格临界性的最小负荷供应量。TSC 曲线［13］的定义为：将配电网所有严格安全边界点的总负荷按从小到大顺序排列后形成的曲线，曲线横坐标为采样点，纵坐标为总负荷。

一条典型的TSC 曲线如图1 所示，图中采样点表示总负荷排序的序号。需要采样点的原因是：TSC 曲线理论上有无数个点，但绘制TSC 曲线时需要有限个点，因此利用采样算法从无数个点中选出有限个采样点，为了更直观地表示供电能力的范围和变化幅度，将采样点按总负荷从小到大的顺序进行排序，再按排序后的顺序描点作图。有学者曾以某馈线负荷为横坐标绘制了描述供电能力的曲线［17］，但未得到广泛应用，以采样点为横坐标的TSC曲线被较多文献采用［12⁃13，18⁃19］，本文沿用此习惯采用TSC曲线描述配电网的供电能力。

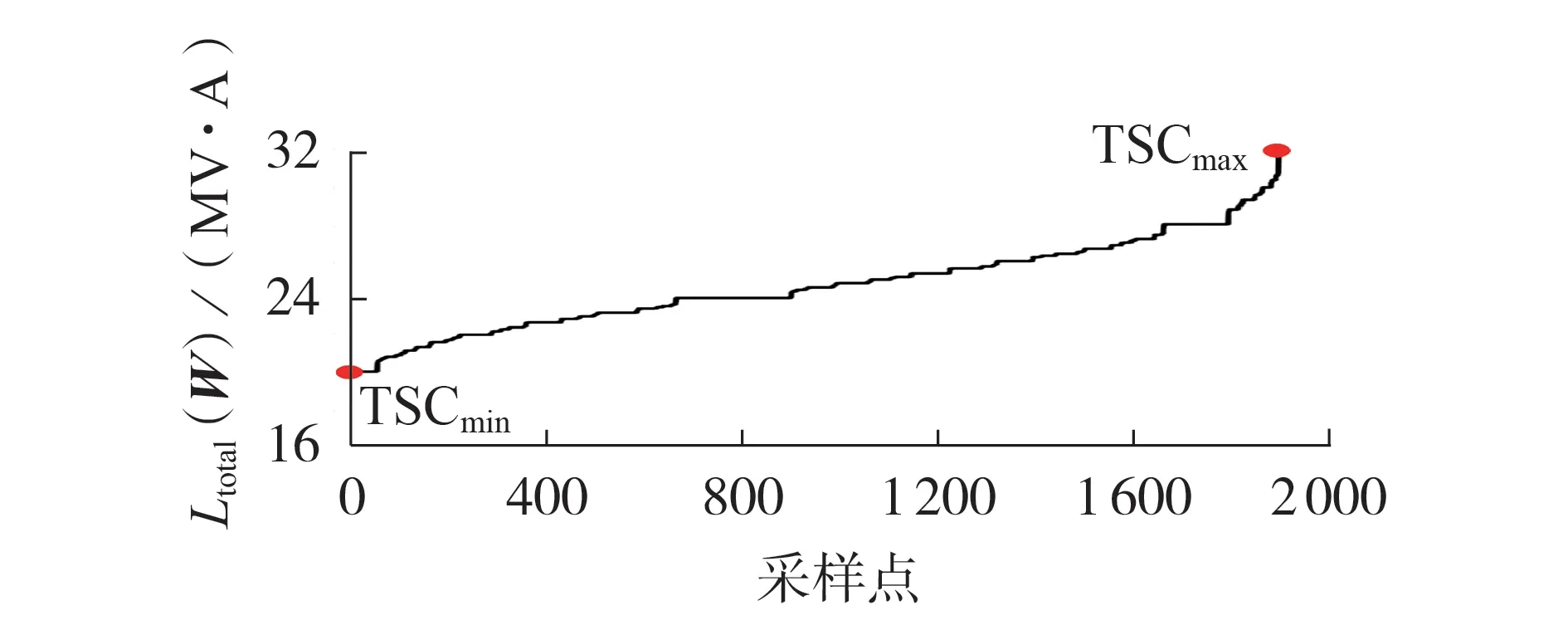
图1 TSC曲线样例Fig.1 Example of TSC curve

2.2 TSCmin的数学模型

根据TSCmin的定义建立数学模型，该模型是在严格边界上以总负荷最小为目标函数的线性规划模型，即：

式中：Keq、Kle、Kgr为相应约束的负荷系数矩阵；Ceq、Cle、Cgr为相应约束的常数列向量；L=[L1，L2，…，Ln]T，为控制变量Li组成的负荷列向量。式（4）中：第1 个和第2 个公式分别为严格边界的等式约束和不等式约束，体现了N-1 转供后安全校验的要求；第3 个公式为负荷转带关系约束；第4 个公式表示馈线负荷非负。本文对联络开关和分段开关之间的节点负荷进行归并，将馈线或馈线段的负荷作为工作点来表示系统状态。

2.3 TSCmin的计算方法

目前已有计算TSC 曲线的方法［12］，计算结果中包含TSCmin，而直接利用TSCmin模型计算TSCmin可大幅提高效率。本文TSCmin计算方法的思路为：完整的严格边界包含若干独立边界，不同独立边界的表达式不同，线性规划模型也不同，因此，先通过安全域表达式求得各严格边界的表达式，再计算每个独立边界βj上的规划模型结果，记为TSCmin，j，最后，选出最小值，即为TSCmin。TSCmin计算流程图如图2所示。

图2 TSCmin计算流程Fig.2 Flowchart of TSCmin calculation

2.4 TSCmin点的求解方法

交叉机理从数学模型的角度解释了TSC 曲线上除TSCmax点之外的其他点相对TSCmax点下降的原因是存在冗余量。TSCmin点是曲线上冗余量最大的点，基于此本文提出TSCmin点的求解方法。由图2可知，在得到TSCmin的同时也得到了TSCmin对应的独立边界（下文简称TSCmin边界）。若仅有1 个TSCmin边界，则该边界上的TSCmin点即为最终结果。若有多个TSCmin边界，则需计算每个边界的TSCmin点，并通过对所有TSCmin点取并集得到最终结果，步骤如下。

1）针对所有的TSCmin边界，得到冗余式并计算最大冗余。由冗余式的定义，得到某独立边界βj上的冗余式Rj。最大冗余由以下模型求出：

该模型是线性规划模型，可利用线性规划软件进行求解。

2）针对所有的TSCmin边界，列写最大冗余方程。TSCmin点满足严格边界约束式（4），由交叉机理可知，TSCmin点满足冗余量取最大值，因此，βj上的TSCmin点满足以下方程：

将式（7）命名为最大冗余方程。其中，第2 个公式表示冗余量取最大值。

3）针对所有的TSCmin边界，求解最大冗余方程。采用一般数学方法求解由式（7）的第1个和第2个公式构成的无约束多元一次方程。该方程一定有解，原因如下：每个边界上一定存在最小值，最小值就是最大冗余方程的解，而无约束多元一次方程是在最大冗余方程的基础上放宽条件，因此无约束多元一次方程也一定有解。在求解后，若无约束多元一次方程有唯一解，则该解也是最大冗余方程的解；否则，将不等式约束用自由变量表示并进行化简，得到自由变量的取值范围，并将其补充到方程解中。

4）对所有TSCmin边界上的结果取并集，得到完整的TSCmin点结果。

将上述方法稍作修改后还可用于求解TSCmax点，如附录A所示。

2.5 TSCmin与TSCmax的关系

TSCmin与TSCmax是对偶关系，体现在以下方面。

1）在定义方面，TSCmin是满足严格临界性的最小负荷供应量，相应地，TSCmax可定义为满足严格临界性的最大负荷供应量，该定义是文献［2］中的定义在N-1准则下的特殊形式。

2）在模型方面，TSCmax模型与TSCmin模型均为线性规划模型，两者的区别如下：在目标函数上，TSCmax模型以总负荷最大为目标函数，TSCmin模型以总负荷最小为目标函数；在约束条件上，TSCmax模型的寻优空间为整个配电网的安全域，TSCmin模型的寻优空间为严格安全边界。

3）在求解方面，TSCmax模型只需进行1 次优化计算，TSCmin模型需对各严格边界进行优化计算，再从各边界的结果中选出最小值，从而得到最终结果。TSCmax点与TSCmin点的求解方法类似，将TSCmin点求解方法中的最大冗余替换成最小冗余即可求解TSCmax点。

3 接线模式算例

考虑到TSCmin是一个新的概念，没有在实际中使用过，采用配电网网架最基本单元的接线模式来展示TSCmin的计算过程并验证正确性。选择两供一备、不对称两分段两联络和对称两分段两联络3 种常见的接线模式，各接线模式概况及TSC 曲线如附录B 所示。利用本文方法得到各接线模式的TSCmin和TSCmin点，再将结果与TSC曲线进行比较验证。

3.1 两供一备接线模式

3.1.1 TSCmin模型及计算结果

两供一备接线模式的3 回馈线等价，可将任意1 回馈线作为备用馈线，另外2 回馈线作为常供馈线。以将负荷L1所在馈线作为备用馈线为例，由安全域DSSR1的表达式得到β1表达式的过程如下：

负荷L2、L3分别仅被DSSR1的第1 个和第2 个公式包含，因此，需要将2 个公式同时变为等式，以满足严格临界性要求。同理，可得到将负荷L2和L3所在馈线作为备用馈线时的独立边界β2和β3。

两供一备接线模式的完整TSCmin数学模型为：

将上述模型分解成β1、β2以及β3上的3个独立优化模型分别进行求解，3 个边界上的优化结果均为1.5 MV·A，因此，两供一备接线模式的TSCmin为1.5 MV·A。

利用TSC曲线计算TSCmin，如附录B第B1.2节所示，所得结果与上述结果相同，验证了本文TSCmin模型和计算方法的正确性。

3.1.2 TSCmin点的计算结果

分别计算3个边界上的TSCmin点，计算过程如附录C 第C1 节所示，结果如附录C 表C2 所示。对3 个边界结果取并集，得到两供一备接线模式的TSCmin点为［0.5，0.5，0.5］ MV·A。与第B1.2 节中TSC 曲线的TSCmin点相同，验证了本文求解方法的正确性。

3.2 不对称两分段两联络接线模式

3.2.1 TSCmin模型及计算结果

不对称两分段两联络接线模式的完整严格安全边界仅包含1个边界β1，其TSCmin数学模型为：

式中：下标“A”“B”表示负荷为同一馈线不同馈线段上的负荷，后同。

可知，不对称两分段两联络接线模式的TSCmin为1 MV·A，与附录B 第B2.2 节中TSC 曲线的TSCmin计算结果相同。

3.2.2 TSCmin点的计算结果

边界β1上的TSCmin点有无穷个，表达式为［（L1A，1-L1A），0，0］（0≤L1A≤1 MV·A）。附录B表B1中由TSC曲线得到的TSCmin点均满足该表达式，验证了本文求解方法的正确性。

3.3 对称两分段两联络接线模式

3.3.1 TSCmin模型及计算结果

对称两分段两联络接线模式在分段模式下的严格边界由边界β1和β2组成，TSCmin数学模型为：

可知，对称两分段两联络接线模式的TSCmin为1.5 MV·A，与附录B 第B3.2 节中TSC 曲线的TSCmin计算结果相同。

3.3.2 TSCmin点的计算结果

分别计算2个边界上的TSCmin点，计算过程如附录C 第C3 节所示，结果如附录C 表C5 所示。对2 个边界的结果取并集，得到对称两分段两联络接线模式的TSCmin点为［（0.5，0），（0.5，0），（0.5，0）］∪［（0，0.5），（0，0.5），（0，0.5）］ MV·A，与第B3.2 节中TSC曲线的TSCmin点相同，验证了本文求解方法的正确性。

4 配电网算例验证

4.1 IEEE-RTBS-BUS4扩展算例

4.1.1 算例概况

采用IEEE-RTBS-BUS4 扩展算例，该算例包含3 站共6 台主变以及8 回10 kV 馈线，每台主变容量均为20 MV·A，每回馈线容量均为9 MV·A，详细网络结构如附录D图D1所示。

4.1.2 TSCmin计算

采用本文方法计算TSCmin和TSCmin点的表达式，并将结果与由TSC 曲线得到的TSCmin和TSCmin点进行比较，以验证本文方法的正确性。

IEEE-RTBS-BUS4 扩展算例的严格边界由边界β1和β2组成，其TSCmin数学模型为：

式（21）和式（22）体现了N-1 安全校验的要求。以馈线F1故障为例，负荷转带关系为L1A→F8（T6），L1B→F6（T4），此时，转带馈线和主变均不应过载，因此有L1A+L8A+L8B≤9 MV·A（F8不过载），L1B+L6A+L6B≤9 MV·A（F6不过载），L1A+L8A+L8B≤20 MV·A（T6不过载），L1B+L6A+L6B≤20 MV·A（T4不过载）。由于算例中每台主变上的出线较少，主变约束不起作用，因此，在表达式中仅体现了馈线约束，即式（21）、（22）中的第1个和第7个公式。其他馈线同理。

对β1、β2上的优化模型分别进行求解。2 个边界上的结果均为36 MV·A，IEEE-RTBS-BUS4扩展算例的TSCmin取上述结果的最小值，即36 MV·A。

4.1.3 TSCmin点的求解

以边界β1为例，按照2.4 节中的步骤求解TSCmin点。

1）针对所有的TSCmin边界，得到冗余式并计算最大冗余。式（21）中严格边界β1上的数学量如表1所示。

表1 边界β1上的数学量Table 1 Mathematical quantities on boundary β1

边界β1上的最大冗余求解模型如式（23）、（24）所示。求解得到Rmaxj=18 MV·A，最大冗余条件为

2）针对所有的TSCmin边界，列写最大冗余方程。将最大冗余条件添加到严格边界表达式中，得到该边界的最大冗余方程，如式（25）所示。

3）针对所有的TSCmin边界，求解最大冗余方程。式（25）第1 — 7 个公式表示的无约束多元一次方程的解为［（9-L8A-L8B，-L7+L8A），9-L7，L3，9-L3，L7，（L7+L8B，9-L7-L8A-L8B），L7，（L8A，L8B）］，含4 个自由变量L3、L7、L8A、L8B。将式（25）第8 — 13个公式用自由变量表示后，化简得到0≤L3≤9 MV·A，L7=4.5 MV·A，L8A=4.5 MV·A，L8B=0。因此，式（25）的解为［（4.5，0），4.5，L3，9-L3，4.5，（4.5，0），4.5，（4.5，0）］（0≤L3≤9 MV·A）。

4）对边界β1和β2上的TSCmin点取并集，得到完整的TSCmin点结果。对2个边界结果取并集，得到最终结果为［（4.5，0），4.5，L3，9-L3，4.5，（4.5，0），4.5，（4.5，0）］∪［（0，4.5），4.5，L3，9-L3，4.5，（0，4.5），4.5，（0，4.5）］（0≤L3≤9 MV·A）。

4.1.4 与现有方法的对比

利用现有方法计算TSC曲线后也可得到TSCmin，采用文献［12］中现有方法得到IEEE-RTBS-BUS4 扩展算例的TSC 曲线，如图3 所示。由TSC 曲线得到的TSCmin为36 MV·A，与本文方法所得结果相同。

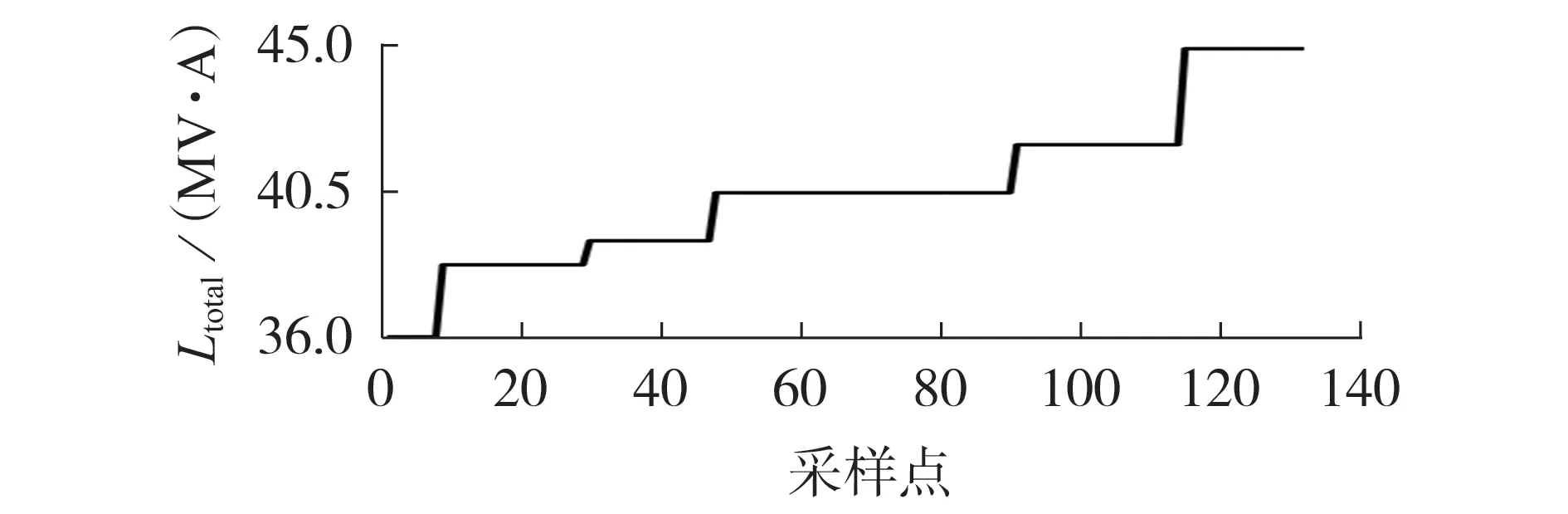
图3 IEEE-RTBS-BUS4扩展算例的TSC曲线Fig.3 TSC curve of IEEE-RTBS-BUS4 extended example

2种方法的TSCmin点结果对比如表2所示。文献［12］方法得到的8个TSCmin点均符合本文TSCmin点的表达式，表2 还给出了上述8 个TSCmin点对应的本文表达式中自由变量L3的取值。如文献［12］方法得到的第1 个TSCmin点［（4.5，0），4.5，9，0，4.5，（4.5，0），4.5，（4.5，0）］ MV·A 是本文TSCmin点的表达式［（4.5，0），4.5，L3，9-L3，4.5，（4.5，0），4.5，（4.5，0）］（0≤L3≤9 MV·A）在L3取值9 MV·A 时的特例。本文方法能得到所有的TSCmin点，且其计算速度也远快于文献［12］方法，文献［12］方法耗时75.356 s，而本文方法耗时0.846 s（测试环境如下：CPU 为AMD Ryzen 7 4800U；内存为16 GB；编程语言为MATLAB）。

表2 2种方法的TSCmin点结果对比Table 2 Comparison of TSCmin point results between two methods

4.1.5 规避TSCmin点的预测控制策略

在TSCmin点，配电网处于供电能力最小的临界安全状态，是运行中应该远离的不利系统状态。在得到TSCmin点后，通过负荷预测可以判断未来某时刻的工作点是否会向TSCmin点靠近。若系统工作点存在向TSCmin点靠近的趋势，则需要提前采取规避措施进行干预，防止系统的N-1安全性被破坏。

根据第3 章中3 种常见接线模式的TSCmin点表达式，给出规避TSCmin点的预测控制策略，如表3 所示。根据表中的策略，通过开关操作调整运行方式，可改变馈线负荷的分布。以下给出IEEE-RTBSBUS4扩展算例的预测控制示例。

表3 规避TSCmin点的预测控制策略Table 3 Predictive control strategy for avoiding TSCmin point

设当前工作点W0=［（0，4），4，2，5，4，（0，4），4，（0，4）］ MV·A，通过负荷预测得到3 h后将达到用电高峰，预测工作点为W1。设预测工作点处的各负荷均为当前负荷的1.2 倍，W1=［（0，4.8），4.8，2.4，6，4.8，（0，4.8），4.8，（0，4.8）］ MV·A。此时总负荷Ltotal=37.2 MV·A，远小于TSCmax的45 MV·A，但N-1 校验已不安全，校验数据如附录E 所示。根据表3 中的策略，在08:00 提前对工作点W0采取预测控制策略：将馈线F2的负荷分别转移1 MV·A至馈线F5和F7，将馈线F1B的负荷转移2 MV·A至馈线F1A，将馈线F6B的负荷转移2 MV·A 至馈线F6A，将馈线F8B的负荷转移2 MV·A 至馈线F8A。得到控制后的工作点W'0=［（2，2），2，2，5，5，（2，2），5，（2，2）］ MV·A，控制后预测时刻的工作点W'1=［（2.4，2.4），2.4，2.4，6，6，（2.4，2.4），6，（2.4，2.4）］ MV·A，经N-1 校验可知，系统处于安全状态，校验数据如附录F所示。

4.2 实际配电网算例

采用2011 年某市某区的实际中压配电网计算TSCmin和TSCmin点，计算过程和结果如附录F 所示。结果表明，本文模型和计算方法对于实际配电网依然适用。

5 结论

TSCmax是在配电网评估时的常用指标，TSCmin是TSCmax的对偶指标，本文首次系统研究了TSCmin，主要结论如下。

1）提出TSCmin的定义和模型，该模型是以配电网严格边界上总负荷最小为目标函数的优化模型，并提出通过对所有边界进行优化求解TSCmin的方法。

2）提出基于最大冗余方程的TSCmin点求解方法，对该方法稍作修改也可用于求解TSCmax点。

3）采用接线模式算例、IEEE-RTBS-BUS4扩展算例和实际配电网算例验证了本文模型和方法的正确性。

4）给出规避TSCmin点的预测控制策略，并结合IEEE-RTBS-BUS4 扩展算例给出示例。该策略能有效防止系统的N-1安全性被破坏。

后续笔者将面向应用深入研究TSCmin点的特征，并将研究范围扩展到有源配电网。

附录见本刊网络版（http：//www.epae.cn）。