计及UPFC最优配置的电力系统鲁棒调度协同优化策略
2024-03-04商立群王建新
商立群,惠 泽,王建新
(西安科技大学 电气与控制工程学院 西安市电气设备状态监测与供电安全重点实验室,陕西 西安 710054)
0 引言
随着系统供需双侧发生快速变化,新能源装机容量和并网规模呈现扩大化趋势,系统输电网架难以适应供需双侧的发展,输电堵塞风险的发生概率大幅度提升[1⁃2]。随着电力电子技术的飞速发展,电力电子装置广泛应用于电力系统的网侧潮流调控中。统一潮流控制器(unified power flow controller,UPFC)作为柔性交流输电系统(flexible AC trans⁃mission system,FACTS)中最为成熟的电力电子设备,因所具备的无功补偿功能、潮流调控特性而受到电力从业人员的广泛关注[3⁃5]。
UPFC 并网优化提升系统潮流效能的前提是其科学合理的规划。目前,国内外的相关研究大多是针对FACTS 元件的单点优化配置、迭代式配置进行研究。其中:启发式算法被应用于FACTS 多点优化配置研究中,提升了非线性交流潮流与FACTS 控制变量的交互耦合水平;微分进化算法[6]、遗传算法[7⁃10]、粒子群优化算法[11]均在FACTS 多点配置中取得了良好的收敛效果。灵敏度法被广泛应用到FACTS 的单点选址优化中,通过构建基于FACTS 控制参数的灵敏度指标以寻找最佳安装点。文献[12]定义了系统传输能力对线路电抗的加权灵敏度指标,用于定位可控串联补偿装置(thyristor con⁃trolled series compensation,TCSC)的最佳布点。文献[13]定义了边际成本的灵敏度指标进行TCSC 选址确定。然而,灵敏度指标法和启发式算法逐次叠加的规划思路割裂了多台FACTS 装置的交叉耦合特性,所得配置方案的全局最优水平值得商榷。
最优潮流(optimal power flow,OPF)法基于矩阵分块技术,建立计及FACTS 等效变量的潮流雅可比矩阵,并基于Matpower 工具包进行求解。文献[14]基于UPFC 的负荷注入模型,实现了计及UPFC等效参数的雅可比矩阵逐次更新,构建了以网损为目标的UPFC 优化配置模型,并基于修正的雅可比矩阵,采用OPF 进行求解。文献[15]基于UPFC 的节点功率注入模型,忽略并联侧的电源等效,并将UPFC等效模型嵌入潮流方程中,建立了新的雅可比矩阵。文献[16]提出了基于静止同步补偿器的节点功率注入模型的潮流求解算法,并将其纳入Newton-Raphson 潮流方程中并加以求解。OPF 法具备较好的求解精度和效率。然而,计及FACTS 参数的OPF计算存在雅可比矩阵的完整迭代,且无法判断FACTS 安装位置及容量对于目标的灵敏性。同时,OPF法对初始值有一定的要求。
随着数学编程算法的飞速发展,FACTS 优化配置的混合整数非线性规划(mixed-integer nonlinear programming,MINLP)问题逐渐取得新进展,通过优化方法实现MINLP 模型的变换,将其转变为混合整数线性规划(mixed-integer linear programming,MILP)等较易求解的数学问题,并采用商业工具包(如CPLEX)进行求解,提升了求解效率。文献[17⁃18]基于TCSC 的等效电抗模型,采用直流潮流法,提出了计及TCSC 最优配置的MILP 模型,并分析了TCSC最优配置对系统经济调度的影响。文献[19⁃20]提出了线性潮流约束方法,用于确定TCSC 的最佳选址、最优容量配置方程。通过对双线性变量进行线性松弛,构建了MILP 模型,但是负荷模式采用单一结构,未考虑其不确定性。文献[21⁃22]考虑系统潮流安全约束,基于Benders 分解法,提出了计及电压源型无功补偿装置的系统OPF 两阶段模型,构建了基于直流潮流法的MILP 主问题和计及交流潮流约束的非线性规划子问题,大幅提升了MINLP 问题的求解能力。
综上所述,FACTS 的多点最优配置应充分考虑各FACTS 单元在潮流调控中的交叉耦合特性[23],计及系统潮流安全约束,建立一种FACTS 并网调控系统的运行表现模型,并采用优化方法来降低模型的求解难度,提升求解效率。为此,本文聚焦UPFC 潮流调控,将UPFC 的最优规划与鲁棒调度相结合,构建规划-调度协同优化模型,提升了网侧参与系统调度的灵活性及源网荷协同运行能力。基于UPFC 的潮流调控特性,提出了计及UPFC 接入的潮流模型,并通过推导构建了计及UPFC 接入的松弛型交流潮流凸优化模型;考虑风电的不确定性特征,构建了计及UPFC 最优配置的电力系统鲁棒调度协同优化模型,并采用列和约束生成(column-and-constraint generation,C&CG)算法进行求解。最后,以IEEE RTS-24 节点系统为算例进行仿真,分析了UPFC 对于新能源消纳、系统调度的影响,验证本文所提模型和求解方法的有效性。
1 计及UPFC接入的潮流方程凸优化技术
UPFC 的等效模型[24]见图1。图中:Vi、Vj分别为UPFC 所在线路两端节点i、j的电压幅值;θi、θj分别为节点i、j的电压相角;Zse、Zsh分别为UPFC 串、并联侧的等效阻抗;Vse、Vsh分别为UPFC 串、并联侧的等效电压源的电压幅值;θse、θsh分别为UPFC 串、并联侧的等效电压源的电压相角。UPFC接入后,交流潮流方程呈现非凸、非线性特点,潮流计算易陷入非确定型多项式难问题。为此,本节构建了计及UPFC的潮流方程,并进行线性化、凸优化变换,建立了计及UPFC 接入的二阶锥规划(second-order cone programming,SOCP)潮流模型,保留了UPFC 的有功、无功调控特性,提升了模型的求解精度和效率。
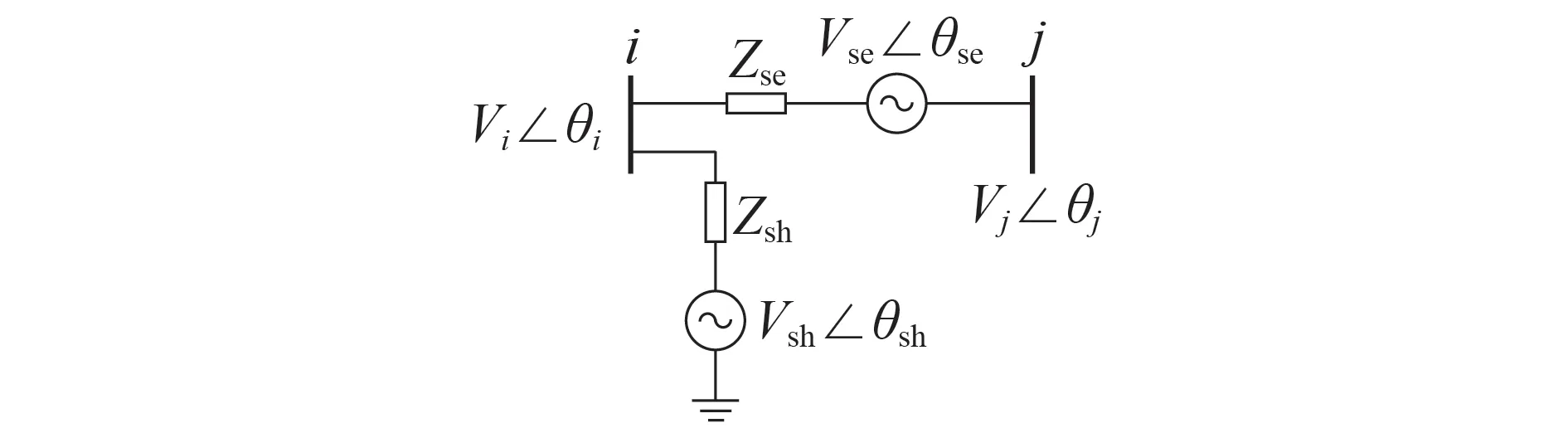
图1 UPFC的等效模型Fig.1 Equivalent model of UPFC
1.1 计及UPFC的交流潮流方程
计及UPFC 的交流潮流方程是非凸、非线性的,存在诸多类似ViVjsin(θi-θj)的非线性变量组。为了降低模型的非线性,本文引入辅助变量Ui、、,如式(1)—(5)所示。
因此,计及UPFC 等效特性的交流潮流模型约束如式(6)—(11)所示。
1)节点电压约束。
式中:V、V分别为节点i电压幅值的上、下限。
2)功率平衡约束。
式中:Pg、Qg分别为发电机组g的有功、无功出力;、分别为节点i的有功、无功负荷;、和、分别为流出和流入节点i的有功、无功功率,表征由UPFC接入发挥的调控特征;、分别为与节点i相连的线路的有功、无功功率;φ(i)为与节点i相连的发电机组集合。
3)线路功率约束。
式中:gij、bij分别为线路ij的电导、电纳。
4)线路最大输电功率约束。
式中:S为线路ij的最大输电功率。
5)UPFC流入节点功率约束。
式中:gse、bse和gsh、bsh分为UPFC 串联侧和并联侧的等效电导、电纳。
6)辅助变量之间的约束。
UPFC接入后,其串联侧和并联侧的等效电压及容量满足如下约束。
1)UPFC等效电压约束。
式中:V、V和、V分别为UPFC 串联侧和并联侧等效电压的上、下限。
2)UPFC串联侧容量约束。
式中:P、Q分别为线路ij上UPFC 串联侧的有功、无功容量;F为线路ij上UPFC 串联侧的最大调控容量。
3)UPFC并联侧容量约束。
式中:P、Q分别为线路ij上UPFC 并联侧的有功、无功容量;F为线路ij上UPFC 并联侧的最大调控容量。
4)UPFC功率守恒约束。
1.2 计及UPFC的潮流模型凸松弛变换
考虑Vi≈1 p.u.、Vj≈1 p.u.及sin(θi-θj)≈θi-θj,则式(2)中的Tij=ViVjsin(θi-θj)可线性化为:
结合式(3)、(4),同时考虑Vi≈1 p.u.、Vj≈1 p.u.,则与、可建立如下近似等效关系:
在交流潮流中,有如下等效关系:
将式(20)代入式(19)中,可得:
结合式(21)和式(22),可建立如下关系:
假设1-(θi-θj)2/2≈1,式(21)可进一步更新为:
观察可知,式(23)和式(24)中仍存在非线性变量组,引入辅助变量Kij、Lij、Hij、Iij、Zij,如式(25)所示。
式中:R、T分别为Rij、Tij的最小值;θmin为电压相角的最小值。
式(25)中的辅助变量满足如下约束:
将式(25)中的辅助变量代入式(23)和式(24),可进一步得到:
式(25)中均为非线性约束,为了降低模型的非凸性,对式(25)进行如下线性松弛以将模型转换为SOCP模型。
类似地,可对式(11)进行如下线性松弛,建立SOCP等效约束,如式(29)所示。
2 计及UPFC 最优配置的鲁棒调度协同优化策略
2.1 计及UPFC最优配置的鲁棒调度协同优化模型
源网荷协同调度应切实考虑源侧、网侧、负荷侧的灵活性资源,从三方面构建调度模型。在计及UPFC最优配置的鲁棒调度协同优化问题中,优化目标应包括机组调度方案的经济性、UPFC 投资、新能源消纳、供电保障水平,以提升源网荷的协同优化水平,提高调度方案的经济性和灵活性,本文以计及系统运行成本、UPFC 投资成本、弃风和切负荷惩罚成本的总成本最小化为优化目标,目标函数可表示为:
需满足的约束条件如下。
1)机组功率平衡约束。
式中:Q为t时刻节点i处机组的无功出力;Pij、Qij分别为线路ij上的有功、无功功率;Q为t时刻节点i处切负荷的无功功率;P、Q分别为t时刻节点i处的有功、无功负荷;P为t时刻 节 点i处的风 电 实际功率;ψ(i)、f(i)分别为以节点i为起点的线路的终点集合、以节点i为终点的线路的起点集合。
2)切负荷约束。
3)弃风约束。
式中:Qshed为t时刻节点i处弃风无功功率。
4)UPFC配置数量约束。
式中:uij为表征UPFC 安装位置的二进制变量,当UPFC安装于线路ij上时uij=1,当UPFC不安装于线路ij上时uij=0;NUPFC为系统中UPFC的最大安装数量;U,max、Umin分别为U的上、下限;U,max、U,min分别为U的上、下限。
5)UPFC配置容量约束。
6)机组调度约束。
机组调度相关约束见附录A式(A1)—(A7)。
由式(8)—(10)、(12)—(17)、(27)—(35)以及式(A1)—(A7)构建的优化模型是确定性混合整数二阶锥规划(mixed integer second-order cone pro⁃gramming,MISOCP)问题。然而,由于风电预测技术难以保证精度,电力系统调度问题中风电呈现高度不确定性,为了提升UPFC 配置方案的适应性水平,本文综合考虑风电波动的所有区间,开展计及不确定参数的UPFC配置研究。
风电的不确定性可用式(36)所示包络约束集合加以描述。
式中:μ为0-1 变量,表征t时刻节点i处风电出力的临界状态,当风电恶劣工况为极大值时,μ=1,当风电恶劣工况为极小值时,μ=0;ΔP为t时 刻节点i处的不确定风电波动范围;P为t时刻节点i处风电功率预测值。
计及式(36)的风电不确定性,原始的确定性MISOCP 优化模型被进一步更新为不确定鲁棒优化配置问题,具体表现为min-max-min形式。鲁棒优化配置的目标函数为:
2.2 基于C&CG算法的两阶段鲁棒优化求解方法
为了便于描述,本文给出了鲁棒优化问题的一般矩阵形式,如式(38)所示。
式中:x为二进制变量向量,主要包括机组启停状态变量、运行状态变量、UPFC 配置落点的状态变量;λ为决策变量向量,即风电波动范围;y为决策变量向量,包括火电机组出力、UPFC 配置容量、弃风量、切负荷量、交流潮流的状态变量;c、d、e为常数系数向量;A、C、G、D、E为计及UPFC 配置的系统调度等式和不等式约束的系数矩阵;b、f、g为对应约束的常数列向量;Qi、qi分别为二阶锥约束中第i个约束的系数矩阵、常数列向量;hi、di分别为第i个二阶锥约束的系数行向量、常数系数;n为二阶锥约束数量。目标函数中第1 个min 问题对应最小化机组启停成本,max 问题用于查找系统的最恶劣工况,第2 个min 问题是为了获取最恶劣工况下的最佳调度方案和UPFC配置方案。
基于CC&G 算法求解鲁棒调度问题式(37),一般将鲁棒模型转换为两阶段问题,通过主问题和子问题的迭代求取最终的优化配置及机组调度方案。
主问题可表示为:
式中:η为Benders割值,表征子问题的最大值;、分别为第l次迭代过程中子问题决策变量y、λ的最优值;x*为x的最优值;m为最大迭代次数。主问题以优化机组启停状态和UPFC 落点为目标,考虑各种最恶劣工况下系统的调度约束,其中,系统最恶劣工况由子问题求得,并以割集的形式传递给主问题,主问题是原优化问题的下界。
一旦主问题求得最优决策方案x,即机组启停计划和UPFC 最优落点,子问题可基于固定的x进一步优化获得λ和y,子问题可描述为:
式中:γ1—γ5为原优化问题对应约束的对偶变量。
由于式(40)中的max-min 优化问题难以直接求解,基于强对偶原理,可通过对偶变换将其转换为max问题,具体对偶模型为:
式中:γ5,i为γ5的第i个元素;di,t和d、d分别为与节点i相连的不确定参数的实际值及其最大值、最小值。
式(41)的目标函数中存在双线性变量组λTγ3,导致模型非线性,难以直接求解。由于鲁棒优化中所有不确定参数的最优解均位于其边界极值处,可采用大M法描述不确定参数最优化过程中的边界状态。
引入二进制变量μi,t,目标函数中的非线性变量组λTγ3在鲁棒问题优化过程中可进一步表示为:
式中:γ3,i为γ3的第i个元素;λ、λ分别为不确定量的最大值、最小值。
式(42)中仍然存在非线性变量组μi,tγ3,i,通过引入松弛变量ωi,t=μi,tγ3,i,基于大M 法对式(42)进行线性松弛,将其变换为如下线性优化模型:
式中:M为惩罚因子。
结合式(41)—(43),原max-min 双层非线性优化模型被转换为一个单层SOCP 优化问题,可采用商用工具包CPLEX进行求解,求解难度大幅降低。
3 算例仿真分析
3.1 模型适用条件及验证
本文所提UPFC 模型的适用条件[25]及验证说明见附录B。通过建立以下3 种潮流模型来评估本文所提潮流模型的有效性和精确性:模型1 为直流潮流模型;模型2 为传统非线性、非凸的交流潮流模型;模型3 为本文所提松弛型SOCP 交流潮流模型。3 种模型均在IEEE 118 节点系统中进行仿真验证,3 种模型的潮流表现见附录C图C1 — C4。
显然,相较于模型2、3,模型1存在较大的差别,这主要是因为直流潮流模型忽略了无功功率。对比图C1和图C2可以发现,模型2、3的线路视在功率和节点电压幅值均呈现高度一致性。由图C3可知,模型2、3 的机组出力方案相差极小,这验证了本文所提模型具备高度拟合传统非线性潮流的特性,且较易求解。对比模型1、2 下的机组出力可以发现,机组出力有较大的差异。
为了验证本文所提模型的精度,定义式(44)所示变量DI,以表征本文所提模型与传统非线性交流潮流模型的间隙。IEEE 118系统中所有线路上有功功率的间隙值见图C4。由图可知,DI几乎全部为0,验证了本文所提模型的精确性。
3.2 计及UPFC最优配置的效能分析
为了验证本文所提模型和方法的有效性,以修改的IEEE RTS-24 节点系统作为UPFC 鲁棒配置的仿真算例,在节点6、8 处分别增加额定容量为400 MW 的风机,其出力波动范围见图2。系统相关数据来自MATPOWER。采用GAMS/CPLEXD 求解MISOCP鲁棒问题,两阶段问题的阈值设置为10-4。
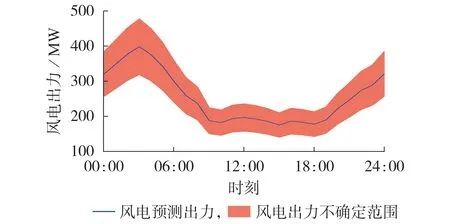
图2 风电预测出力及不确定范围Fig.2 Forecast output and uncertainty range of wind power
3.2.1 UPFC 最优配置对系统鲁棒调度方案的效能分析
计及风电、负荷不确定性的鲁棒调度计划中,UPFC 的优化配置对机组启停计划会产生重要的影响。不同UPFC 配置方案对机组运行状态的影响见图3。由图3 可知,与无UPFC 配置方案相比,配置1 — 3台UPFC大幅改变了机组的启停计划。在不同的UPFC配置方案下,除机组G7、G11运行状态发生变化,其他机组的启停状态保持一致。
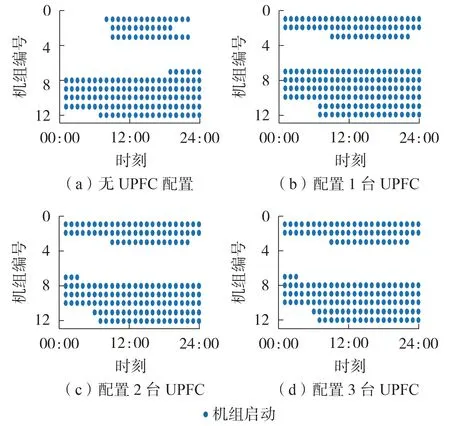
图3 不同UPFC配置方案对机组运行状态的影响Fig.3 Influence of different UPFC configuration schemes on unit operating status
当无UPFC 配置时,机组启停成本为15 889 元;当配置1 台UPFC 时,G1、G2、G7、G11的运行状态发生变化,机组启停成本下降为7 931 元;当配置2、3 台UPFC 时,相较于配置1 台UPFC,机组G7、G11的启停状态发生了改变,启停成本也提高到8 243元。
当配置2、3 台UPFC 时,2 种配置方案下机组的启停状态完全一致,这表明基于UPFC 潮流调控特性的鲁棒调度已经接近系统的极限值。不同UPFC配置方案下鲁棒调度的目标函数值和机组启停成本结果如表1所示。
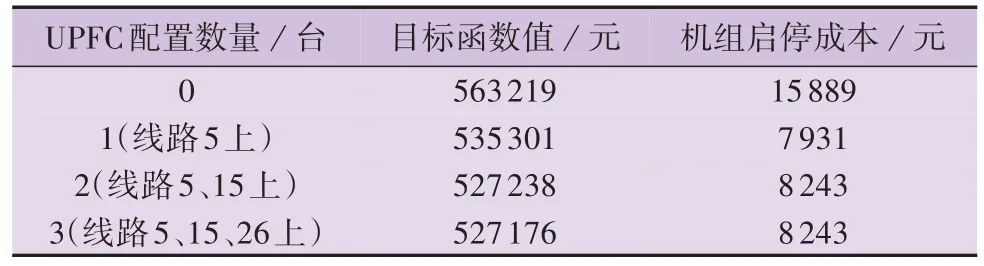
表1 不同UPFC配置方案下鲁棒调度的目标函数值和机组启停成本Table 1 Objective function value and unit startup and shutdown cost of robust scheduling under different UPFC configuration schemes
由表1 可知,随着UPFC 配置数量的增加,系统的总运行成本减小,但下降幅度逐渐变小。相较于配置2 台UPFC 的方案,配置3 台UPFC 方案的目标函数值几乎未发生变化,表明UPFC 对系统潮流优化、转移的能力已接近极限。
3.2.2 UPFC最优配置对系统鲁棒调度计划的影响
最优鲁棒调度方案中的不确定量一般位于其边界极值处。不同UPFC 配置方案下最后1 次迭代的最恶劣工况见图4。由图可知,在不同UPFC 配置方案下,风电的最恶劣工况未发生明显变化,仅是配置2、3 台UPFC 的方案中,23:00 时刻风电取得极小值,表明UPFC并网后系统面对的恶劣工况发生变化。
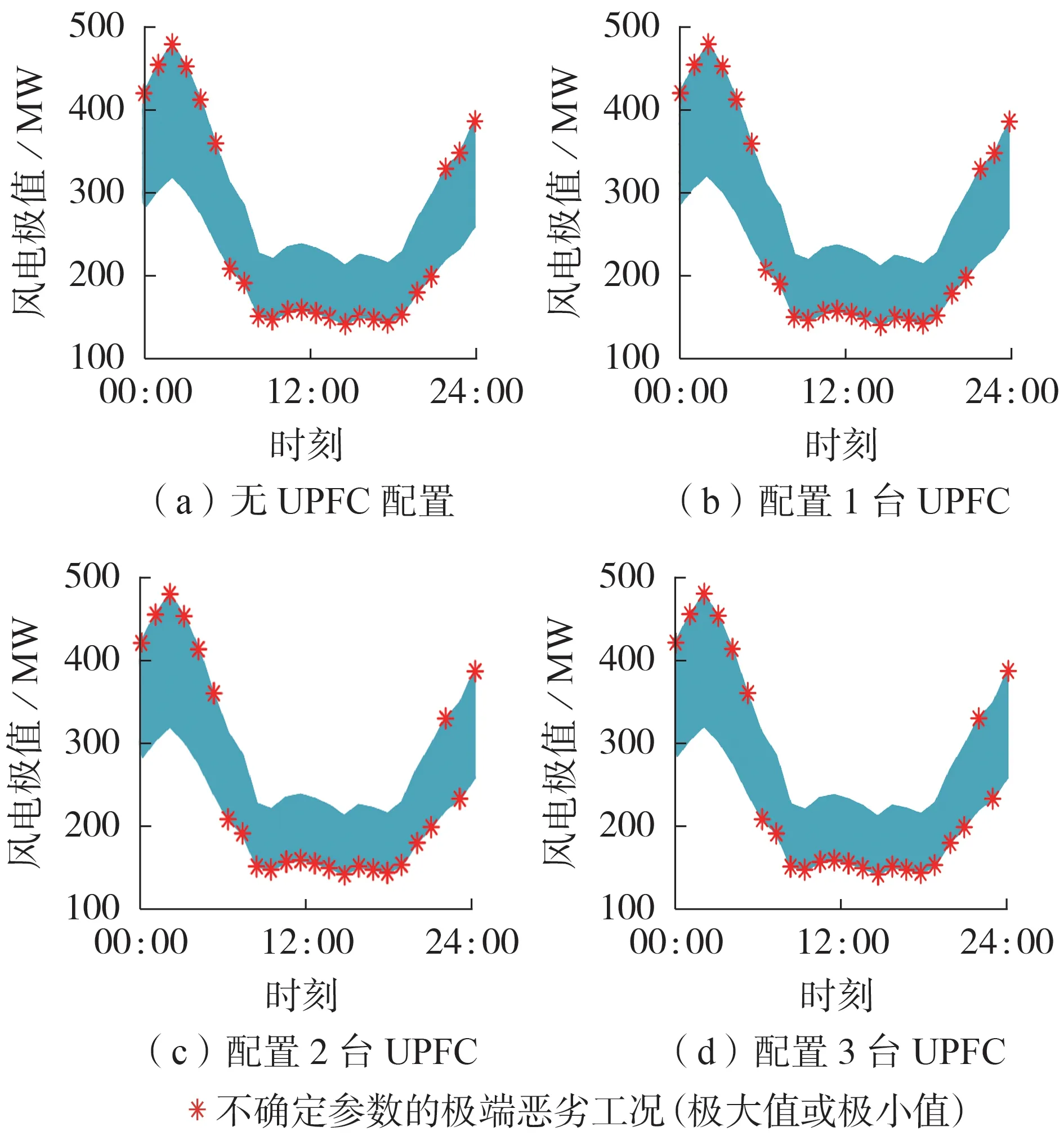
图4 不同UPFC配置方案对不确定参数极值的影响Fig.4 Influence of different UPFC configuration schemes on extreme values of uncertain parameter
为了进一步评估UPFC 最优配置对风电消纳、负荷供给水平的效能,首先分析UPFC 最优配置对弃风、切负荷现象的作用。以最后1 次迭代的最恶劣工况为例,不同UPFC 配置方案对系统运行结果的影响如表2所示。由表可知,随着UPFC 配置数量的增加,弃风功率和切负荷功率明显改善。当无UPFC 配置时,弃风功率、切负荷功率分别为31.15、1.75 MW;当在线路5 上配置1 台UPFC 时,弃风功率、切负荷功率分别下降至28.97、0.03 MW;当配置2、3 台UPFC 时,弃风功率进一步减少为27.76 MW,同时系统中不存在切负荷风险。可见,UPFC最优配置大幅降低了系统弃风和切负荷风险。对比1 台UPFC 配置方案,2 台UPFC 配置方案的机组运行成本增加,这主要是因为系统为了减小弃电量水平,只能牺牲部分火电机组的经济性。与配置2 台UPFC方案相比,当配置3台UPFC 时,弃风功率、切负荷功率没有发生变化,但系统运行成本减少,这主要是因为线路26 上配置的UPFC 对于潮流的调控作用,改善了机组的出力计划,从而提高了经济性。
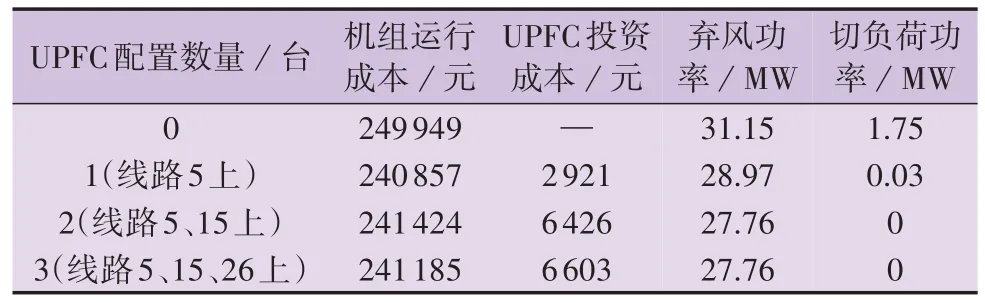
表2 不同UPFC配置方案对系统运行结果的影响Table 2 Influence of different UPFC configuration schemes on system operating results
在本文所提鲁棒调度问题中,不同UPFC 配置方案对风电消纳的影响如图5 所示。由图可知,随着UPFC 配置数量的增加,风电消纳水平整体上保持上升趋势,当UPFC 配置数量为0 — 3 台时,风电总消纳量分别为94.06、96.24、96.32、96.32 MW,风电消纳能力明显提升。可见,当配置2 台UPFC 时,系统的风电消纳、供电保障水平已达到最大,配置3 台UPFC只能调整局部机组的出力计划,从而提升机组的运行经济性。
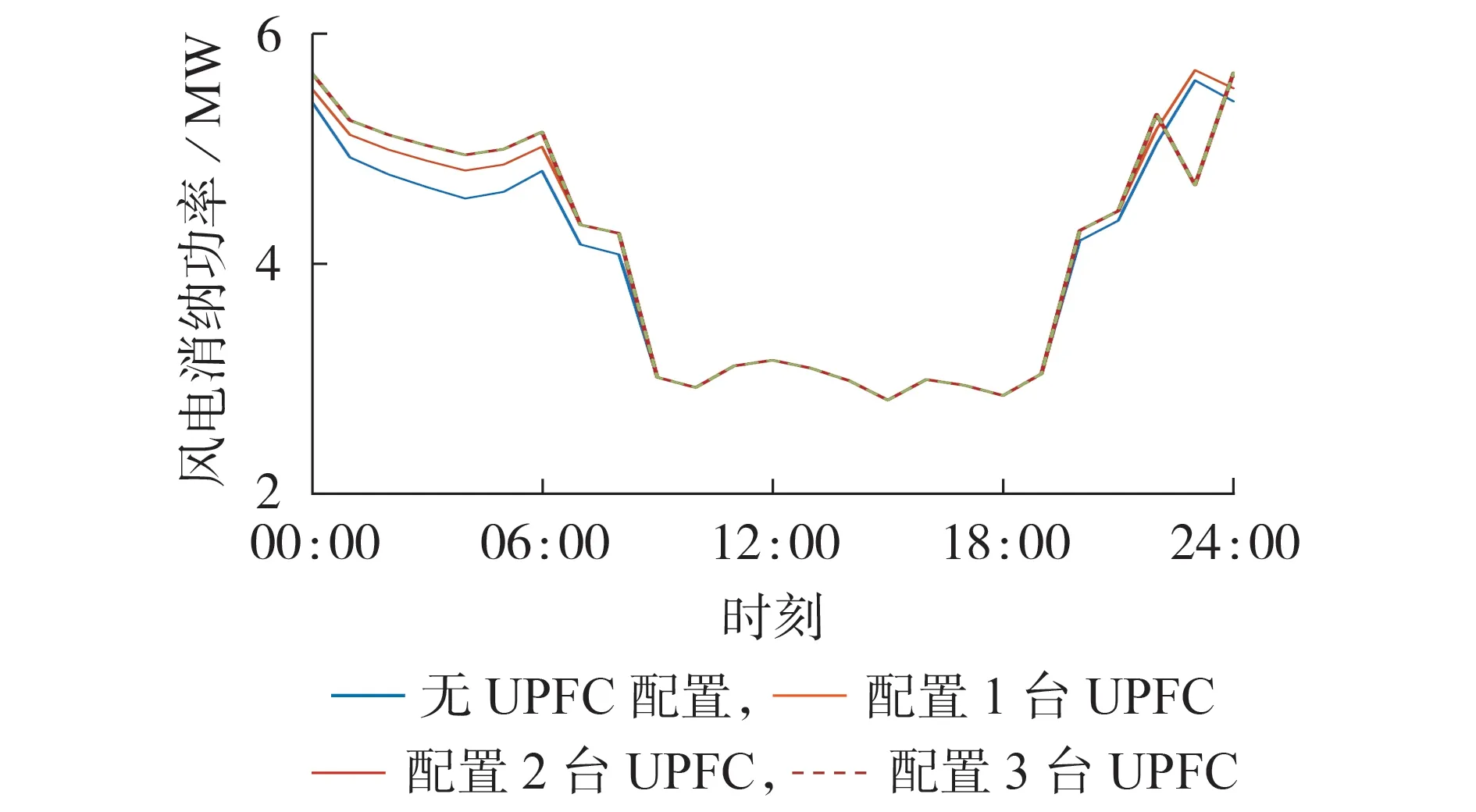
图5 不同UPFC配置方案对风电消纳的影响Fig.5 Influence of different UPFC configuration schemes on wind power consumption
4 结论
针对UPFC 并网规划及协同参与系统调度的问题,结合风电不确定性,本文提出了一种新的UPFC并网优化以提升系统调度灵活性的策略,并基于IEEE RTS-24节点系统进行算例仿真,所得结论如下:
1)本文所提计及UPFC 的松弛型交流潮流模型与初始的非线性潮流模型的拟合度极高,且模型求解效率、精度得到大幅提升;
2)在考虑UPFC 最优配置的电力调度中,UPFC显著提升了网侧的调控灵活性,有效提升了风电消纳能力和系统运行经济性,增强了供电保障能力;
3)所提策略中UPFC 的配置方案保持延续特征,从而保留了多台UPFC 装置间的交叉耦合特性,提升了规划方案的最优化水平。
附录见本刊网络版(http://www.epae.cn)。
