基于超越方程极点分布间接判定的分布式电站谐波不稳定分析方法

徐方维，陈 锴，郑鸿儒，周 全，陈 超，龚利武，张 炜，唐 昕，3

（1.四川大学 电气工程学院，四川 成都 610065；2.国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314000；3.浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

“双碳”目标驱动下，以光伏和风电为代表的分布式电站发展迅速［1］。分布式发电单元通过并网逆变器将清洁能源馈入电网的同时，也向电网注入了宽频域、高频次谐波［2］。由于线路的分布参数特性，逆变器与电网交互可能在几Hz 到数kHz 范围内存在多个截止频率点，进而发生多频点谐波放大，这种现象在分布式电站经长线路并入弱电网时尤为突出。若截止频率下系统呈现负阻尼，则谐波将持续放大，导致电压、电流波形严重恶化，这种现象被称为谐波不稳定。谐波不稳定可造成设备损毁，危及电网稳定运行。因此，准确分析分布式电站稳定性及潜在谐波放大点，可为谐波不稳定评估、谐波管控及治理等提供重要的理论指导。

目前，谐波不稳定的研究方法主要有状态空间法［3⁃4］和阻抗分析法［5⁃8］2 种。前者是在dq轴时域下建立小信号状态空间模型，通过计算特征矩阵的特征根，判断系统的稳定性与谐波放大点。文献［3⁃4］通过建立并网逆变器系统的状态空间模型，并分析时延、控制系统、滤波器、电网强度等参数对谐波不稳定影响。阻抗分析法是在dq轴频域下以公共连接点（point of common coupling，PCC）为界分别建立两侧小信号等效电路模型，结合阻抗稳定判据判定系统稳定性、截止频率和相位裕度［5］。文献［6］对多并网逆变器系统谐波不稳定现象进行评估，但其未考虑锁相环（phase-locked loop，PLL）的影响。为此文献［7⁃8］进一步分析PLL 对系统谐波不稳定影响。

计及线路分布参数模型是分析谐波不稳定的必要条件［9］，然而，模型引入使系统极点方程变为含复数双曲函数的超越方程，导致谐波不稳定评估面临极点分布难以确定问题。这一点虽已在大量文献中提到，但其重点在于分析线路分布参数对谐波放大的影响，无法判断系统稳定性，仅有少量文献在考虑线路分布参数后对系统稳定性展开研究。例如：文献［9］将双曲函数欧拉展开，建立系统特征根与频率的联系，从而确定极点分布；但其欧拉展开过程忽略了传播系数中拉普拉斯算子的实部，仅能求出复平面虚轴附近的部分系统极点，无法充分判定系统稳定性；文献［10⁃13］基于奈奎斯特稳定判据（Nyquist stability criterion，NC）间接判定系统稳定性，或基于伯德图截止频率处的相位裕度判定系统稳定性。但文献［9⁃13］均忽略了dq轴耦合影响，无法准确判定系统稳定性。而计及dq轴耦合时，无法将系统解耦为独立的d轴和q轴2 个单输入单输出子系统进行分析，导致传统NC失效［14］。

虽然关于dq轴阻抗耦合建模及稳定分析有大量研究，但还未有研究将其扩展应用于同时考虑dq轴阻抗耦合和线路分布参数的场景。为此，本文建立了同时计及dq轴耦合和线路分布参数影响的分布式电站阻抗模型，并验证模型准确性。针对含双曲函数的闭环传递函数矩阵行列式极点分布不易求解问题，提出基于广义奈奎斯特稳定判据（generalized Nyquist stability criterion，GNC）的系统极点分布间接判定方法，通过回率矩阵行列式特性，间接判定闭环传递函数矩阵行列式的极点分布。进一步分析不同线路长度和电网强度下，dq轴耦合和线路分布参数对谐波不稳定的影响。最后，基于电磁暂态仿真平台搭建分布式电站仿真模型，验证所提方法的有效性和准确性。需要指出的是，GNC 是较为成熟的稳定性分析方法，本文的创新点并非稳定理论的提出，而在于将GNC 用于间接判定系统超越方程极点分布以实现谐波不稳定分析，并给出复杂闭环传递函数矩阵的回率矩阵和稳定条件判定的详细过程，使所提方法切实可行。

1 分布式电站阻抗模型

1.1 单台并网逆变器输出等效模型

图1 为单台并网逆变器的主电路及其控制系统。图中：L1、L2分别为逆变器侧和电网侧的滤波电感；Cf、Rd分别为滤波电容及其寄生电阻；Udc为直流侧输入电压；Irdef、Irqef分别为参考电流Iref的d、q轴分量；s1、s2、…、s6为开关管信号；I1、IC分别为逆变器输出电流和电容电流；Uinv为逆变器输出电压；UC为电容电压；Uo、Io分别为PCC 处电压和电流；θPLL为Uo相位；Uw、Zw分别为电网电压和等效阻抗。

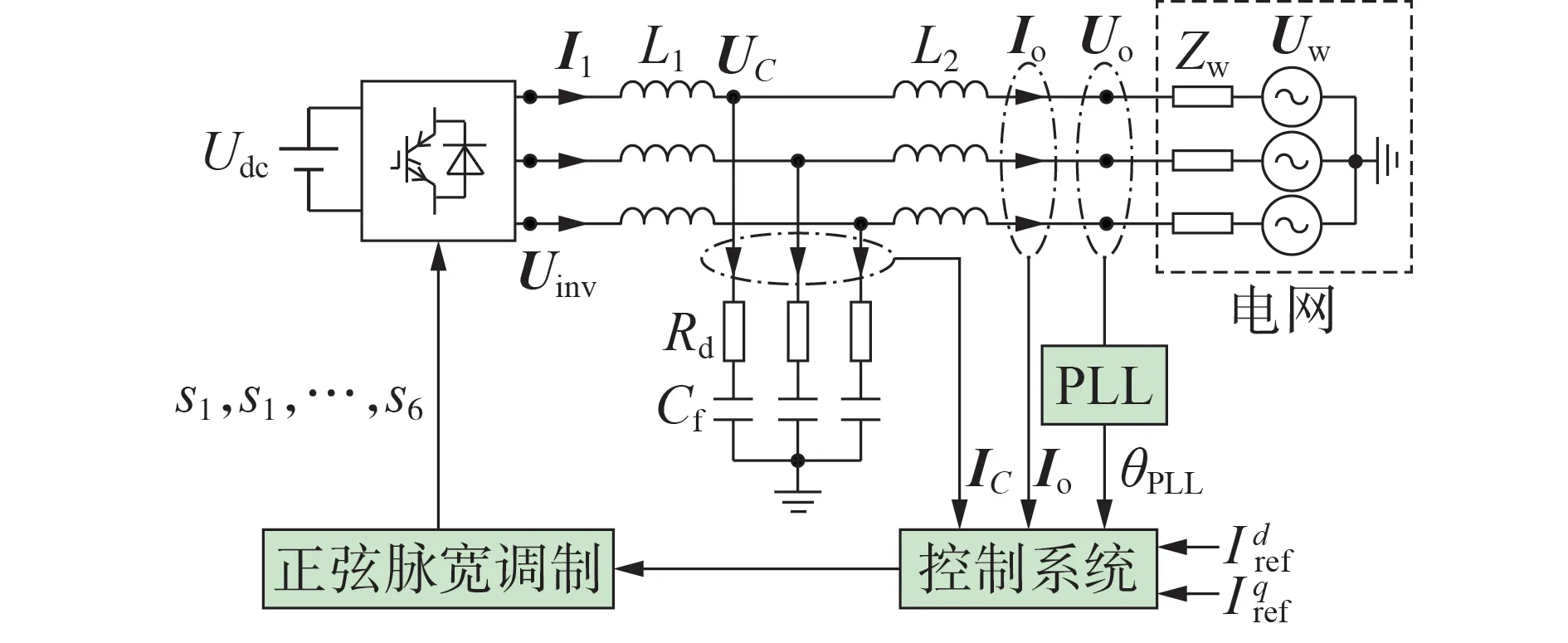
图1 单台并网逆变器的主电路及控制系统Fig.1 Main circuit and control system of single grid-connected inverter

由图1可得主电路在dq轴下的表达式为［7］：

式中：ω1为基波角频率；为了表达简洁，本文所有加粗斜体的电压、电流变量均表示dq轴下的2×1 维矩阵，矩阵中的元素为变量的d、q轴分量，例如，Uinv=。可见，矩阵非对角线元素非零，d轴与q轴分量之间存在交互影响，即d、q轴之间存在耦合。

并网逆变器闭环控制输出特性可利用诺顿电路等效，详细推导见附录A，其中并网电流Io为：

式中：Ginv和Yinv分别为单台并网逆变器输出等效电流源系数和输出导纳。

1.2 分布式电站等效电路

图2 为n台并网逆变器经线路并网的分布式电站电路模型。图中：Upcc、Ipcc分别为分布式电站PCC处的电压、电流；Geq、Yeq分别为逆变器侧等效电流源系数和输出导纳；Zeq_g为等效电网阻抗。其中，并网逆变器采用诺顿等效模型；变压器模型采用串联短路阻抗和并联励磁阻抗τ型电路等效，由于励磁阻抗相对较大，可视为开路，且串联电抗远大于串联电阻，仅将箱变和主变等效为串联纯电抗模型，分别用ZDT和ZMT表示；35 kV 线路采用π 型电路结构表示，其串联阻抗和并联导纳分别用Zs和Yp表示；110 kV电网采用理想电压源串联阻抗的戴维南电路模型，电压和阻抗分别用Ugrid和Zg表示。

图2 分布式电站电路模型Fig.2 Circuit model of distributed power plants

线路分布参数模型的Zs和Yp分别为［9］：

式中：l为线路的长度；Zc为线路的特征阻抗；γ为传播系数：I为2×2维单位矩阵。Zc和γ分别为：

式中：R0、L0和C0分别为单位长度线路的电阻、电感和电容。

逆变器侧等效电流源系数Geq和输出导纳Yeq的表达式分别为：

根据图2（b），可以推导出Ipcc的表达式为：

为验证所建立的分布式电站阻抗模型准确性，利用谐波小信号注入法［15］测量逆变器侧dq轴阻抗Zeq(Zeq=Y)的幅频特性，并与理论模型阻抗幅频特性进行对比验证，具体参数见附录B 表B1。测量与模型阻抗的幅频特性对比见附录B 图B1。由图B1可知：所建立模型与测量阻抗幅频特性基本吻合，验证了所建模型的准确性。

2 基于GNC的系统极点分布间接判定方法

2.1 谐波稳定性研究难点及解决思路

从式（7）可知，系统稳定性由矩阵Geq、Yeq和TF共同决定，稳定的条件为：①条件1，行列式|Geq|、|Yeq|均无右半平面极点；②条件2，行列式|TF|无右半平面极点。

实现条件1和条件2的准确判断，难点在于：

1）计及dq轴耦合时，由式（2）可知，矩阵非对角元素非零，致使矩阵Geq、Yeq和TF非对角元素非零，此时d轴和q轴2 个子系统不独立，无法将系统解耦为独立的d轴和q轴2 个单输入单输出子系统，传统NC失效；

2）由式（6）、（8）可知，考虑线路分布参数所引入的双曲函数使得Geq、Yeq和TF极点方程为超越方程，无法得到极点方程中拉普拉斯算子s的解析解，致使极点分布难以确定，文献［9］将双曲函数通过欧拉展开以确定极点分布，但忽略了拉普拉斯算子的实部，导致无法充分判定系统稳定性（理论分析和算例验证见附录C）。

GNC 是传统NC 的推广，在多输入多输出系统中，无论各子系统是否独立，均可以利用GNC 判定系统稳定性，可有效解决计及dq轴耦合时NC 失效问题［16⁃17］。此外，根据GNC原理，其可在已知回率矩阵极点分布的情况下，结合回率矩阵的特征函数奈奎斯特曲线对临界点（-1，0）包围情况，间接判断闭环传递函数矩阵是否存在右半平面极点，可解决计及线路分布参数时极点分布难以确定问题。需要指出的是，“间接”指不直接求解极点的具体值，而是借助GNC，判断闭环传递函数矩阵行列式是否存在右半平面极点。

为此，基于GNC 特点，本文在同时计及dq轴耦合和线路分布参数下提出基于GNC 的系统极点分布间接确定方法，进而准确评估分布式电站谐波不稳定问题。

2.2 GNC原理

GNC 指 出［18］，当 闭 环 传 递 函 数 矩 阵 行 列 式|I/(I+L)|极点不易获取时，可在已知回率矩阵行列式|L|极点分布的情况下，结合回率矩阵L的特征函数奈奎斯特曲线对临界点（-1，0）包围情况，间接判断行列式|I/(I+L)|是否存在右半平面极点。设回率矩阵为：

式中：Ldd、Ldq、Lqd、Lqq为回率矩阵L中的元素。则回率矩阵L的特征函数为：

当且仅当特征函数l1、l2的奈奎斯特曲线在复平面逆时针环绕（-1，0）的圈数总和，与回率矩阵行列式|L|右半平面极点个数相同时，可判定行列式|I/(I+L)|不存在右半平面极点，即系统是稳定的，否则系统不稳定。

对于复杂的奈奎斯特曲线，为便于分析，可用正频率响应奈奎斯特曲线的正、负穿越次数判定系统稳定性。正、负穿越次数分别用N+和N-表示。当且仅当2N+-2N-与回率矩阵行列式|L|右半平面极点个数相同时，可判定行列式|I/(I+L)|不存在右半平面极点，即系统是稳定的，否则系统不稳定。

当系统稳定时，奈奎斯特曲线与单位圆交点决定系统的截止频率和相位裕度，截止频率处的谐波存在谐波放大风险，且相位裕度越小，谐波放大风险越高。简而言之，截止频率点对应系统潜在谐波放大频率点。由图2（b）可知：显然式（7）中GeqIref为逆变器侧的等效谐波电流发射源；而Yeq为逆变器侧等效导纳，YeqUgrid为电网背景谐波电压Ugrid施加在Yeq时产生的谐波电流，因此可将其视为网侧谐波电流发射源；当逆变器并网工作时，PCC 谐波电流不仅与两侧等效谐波发射源有关，还受两侧谐波阻抗参数共同影响，即两侧谐波存在共同交互作用，即由式（7）中TF体现。因此，两侧谐波共同作用时，PCC 处谐波电流放大特性主要取决于TF的回率矩阵奈奎斯特曲线与单位圆交点。

需要注意的是，虽然已有许多相关研究基于条件1及条件2进行稳定性分析，但是在分析并网系统稳定性时，并未同时计及dq轴耦合和线路分布参数影响，且通常直接对条件2 进行稳定性判定，潜在假设条件1 成立［5，16］，而实际由于逆变器控制、线路分布参数等因素影响，条件1 可能不成立。为此，本文在同时计及dq轴耦合和线路分布参数影响下，基于上述GNC 原理详细推导稳定条件1 和条件2 判定过程。

2.3 条件1判定

在推导条件1判定之前，有3个已知信息：

1）复数双曲函数sinh(γl)和cosh(γl)均无右半面的零点和极点（具体推导见附录D）；

2）由式（5）可知，线路的特征阻抗Zc不存在右半面的零点和极点；

3）单台逆变器的输出导纳|Yinv|和输出电流源系数|Ginv|不存在右半平面极点［7］。

系统稳定的条件1 要求行列式|Geq|和|Yeq|均无右半平面极点，观察式（6）可知，|Geq|和|Yeq|极点方程一致，因此二者稳定性判定只需判定其一即可。

根据前述3 个已知信息，Zc、|Yinv|和sinh(γl)均无右半平面极点，可以将式（6）中Geq或Yeq表达式的分子、分母同时除以nZcYinvsinh(γl)，则其回率矩阵LGeq为：

当|I+YinvZDT|不存在右半平面极点时，可以将式（6）中Geq或Yeq表达式的分子、分母同时除以(I+YinvZDT)cosh(γl)，则其回率矩阵L'Geq为：

观察式（11）与式（12）可知：

1）|I+YinvZDT|的右半平面极点与|Yinv|的右半平面零点之和，即为|LGeq|的右半平面极点个数；

2）|I+YinvZDT|的右半平面零点与|Yinv|的右半平面极点之和，即为|LG'eq|的右半平面极点个数。

当且仅当LG（eq或LG'eq）的特征函数奈奎斯特曲线在复平面逆时针环绕（-1，0）的圈数，或其正频率奈奎斯特曲线表达式2N+-2N-的值与|LGeq（|或|L'Geq）|右半平面极点个数相同时，条件1成立，否则不成立。

上述2 种回率矩阵为互逆关系，这实际上是GNC 和反广义奈奎斯特稳定判据（generalized in⁃verse Nyquist stability criterion，GINC）的关系，二者判定结果是一致的［19］。

2.4 条件2判定

条件2 要求行列式|TF|无右半平面极点，即只要TF的回率矩阵满足GNC 即可。TF的回率矩阵LTF为：

在利用LTF奈奎斯特曲线判定条件2 之前，需要先确定LTF的极点分布情况，根据式（13）可知，回率矩阵LTF的极点方程仍然为超越方程，其极点分布难以获取。但是观察式（6）与式（13）可知，闭环传递函数矩阵Geq、Yeq与回率矩阵LTF极点方程一致。因此，若条件1 不成立，即|Geq|和|Yeq|存在右半平面极点，则判定系统不稳定，无须进行后续条件2 判定；若条件1 成立，则可判定|LTF|无右半平面极点，若回率矩阵LTF的奈奎斯特曲线均不包围（-1，0）（或顺时针包围与逆时针包围圈数相同时），则LTF传递函数矩阵满足GNC，即稳定条件2 成立。最后可根据LTF的奈奎斯特曲线给出系统截止频率和相位裕度。所提谐波不稳定评估流程见图3。

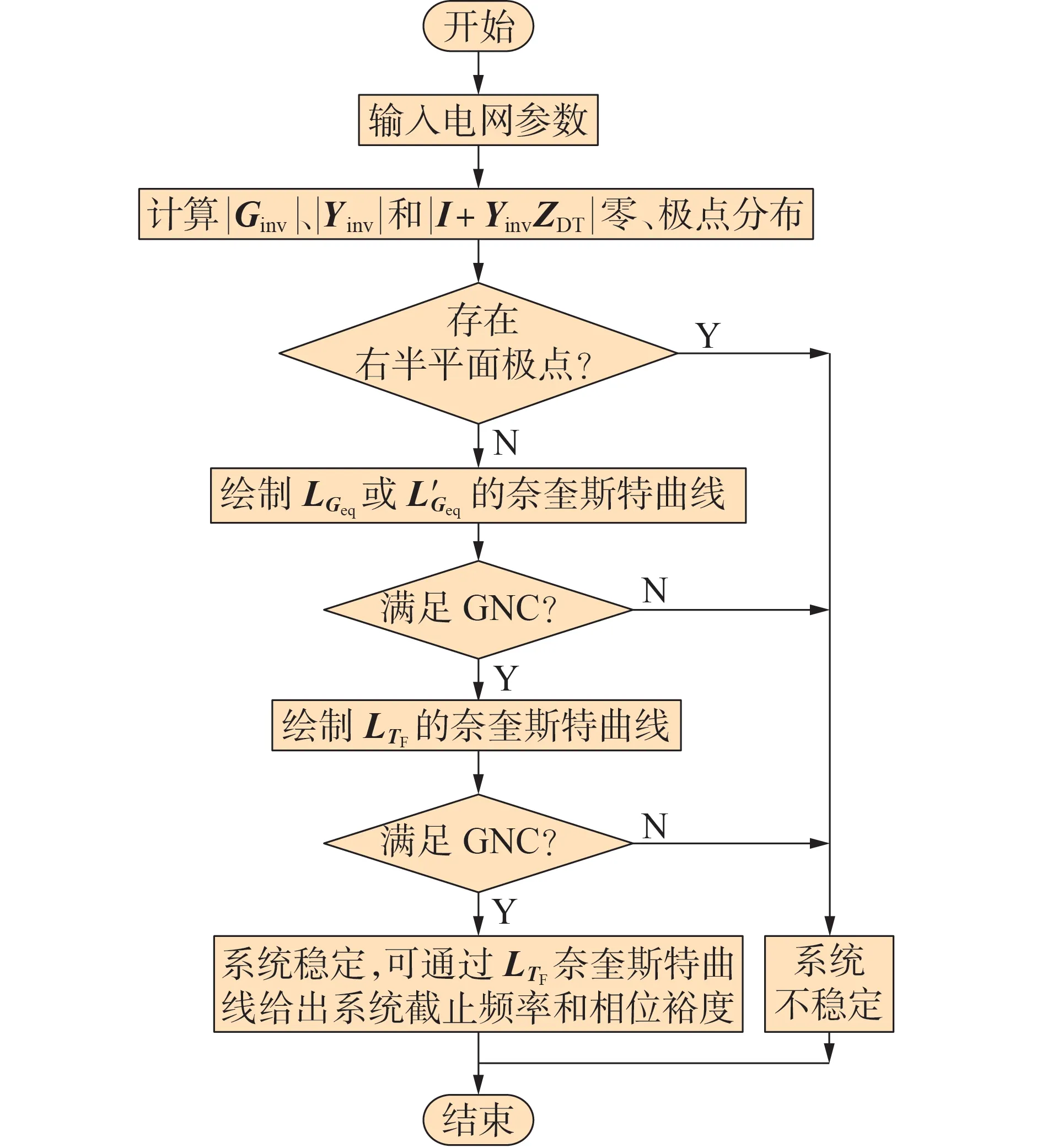
图3 分布式电站谐波不稳定评估流程Fig.3 Harmonic instability assessment process of distributed power plants

3 dq 轴耦合及线路分布参数对谐波不稳定影响分析

PCC 处电网强度通常采用短路比SSCR表征，即电网短路容量SSC与并网逆变器总额定容量nSN之比：

通常情况下，SSCR＜ 3 可视为弱电网［20］。对于三相系统，若已知网侧额定电压Ugrid，则等效电网阻抗Zeq_g与电网的短路容量关系如下：

为重点分析不同线路长度及电网强度下dq轴耦合和线路模型对谐波不稳定影响，不妨假设分布式电站并网逆变器的工况以及容量、控制及系统等参数不变，具体参数见附录B 表B1，分析过程中全部参数均归算到35 kV侧。

由前文分析可知，谐波不稳定评估分为对条件1 及条件2 的判定，且条件1 不涉及电网强度。因此首先研究不同线路长度下dq轴耦合和线路模型对条件1的判定结果影响。

当同时考虑dq轴耦合且线路采用分布参数模型时，分别计算|Ginv|、|Yinv|和|I+YinvZDT|的零、极点，并判断是否存在右半平面零、极点，判断结果见表1。表中：“×”表示不存在；“√”表示存在。

表1 |Ginv|、|Yinv|和|I+YinvZDT|的零、极点Table 1 Zeros and poles of |Ginv|，|Yinv| and |I+YinvZDT|

由表1 可知：行列式|Ginv|、|Yinv|均不存在右半平面极点，逆变器自身可稳定运行，满足设计要求；|I+YinvZDT|无右半平面零极点，|Yinv|仅存在1 个右半平面零点，故行列式|LGeq|仅存在1个右半平面极点，行列式|LG'eq|不存在右半平面极点。因此，当且仅当LGeq的正频率奈奎斯特曲线正穿越次数N+比负穿越次数N-多0.5（此时，2N+-2N-=1，与行列式|LGeq|右半平面极点个数相等）；或者，当且仅当LG'eq的全频率响应奈奎斯特曲线均不包围（-1，0）或顺时针包围圈数与逆时针包围圈数相等时，条件1 成立，否则不成立。由于LGeq的奈奎斯特曲线较为复杂，因此只绘制其正频率响应奈奎斯特曲线；而LG'eq则绘制其全频率响应奈奎斯特曲线。

下面分别以线路长度l为20 km 和50 km 为例，绘制LGeq与L'Geq的奈奎斯特曲线，如附录E 图E1 所示。由图可知：当l分别为20 km 和50 km 时，LGeq的正频率响应奈奎斯特曲线正穿越次数均比负穿越次数多0.5（N+=2，N-=1.5）；L'Geq的奈奎斯特曲线均不包围（-1，0）。因此条件1 成立，即行列式|Geq|和|Yeq|均无右半平面极点。

相似地，对于不考虑dq轴耦合但采用分布参数模型、考虑dq轴耦合但不采用分布参数模型、既不考虑dq轴耦合也不采用分布参数模型3 种情况，经过分析后条件1 判定结果均一致。需说明的是：不同线路长度将影响LGeq与LG'eq的奈奎斯特曲线的变化。在设计规划电力系统时，线路输电距离取决于其所在电压等级，例如，对于35 kV系统，其输电距离为20～50 km［21］。为此，本文在线路长度为5～50 km的电力系统中做了大量的仿真遍历，条件1 均成立。在条件1 均成立的前提下，可判定LTF无右半平面极点，系统的谐波不稳定特性取决于LTF奈奎斯特曲线包围（-1，0）情况，若包围（-1，0），则系统不稳定，否则系统稳定，且LTF奈奎斯特曲线与单位圆交点决定系统潜在谐波放大点。

其次，研究dq轴耦合和不同线路模型对条件2的判定结果影响。当l分别为20 km 和50 km，电网强度（通过调整SSC调节该参数）不同时，dq轴耦合／解耦与不同线路模型的LTF奈奎斯特曲线如附录E 图E2 所示。由图可知：dq轴耦合／解耦或采用不同线路模型，系统稳定性判定结果均存在矛盾。

为进一步分析在更广线路长度范围和电网强度下，dq轴耦合和线路模型对系统稳定性影响，本文在l为5～50 km 和SSCR为1～8 条件下做了大量的仿真遍历，仿真结果如图4所示。

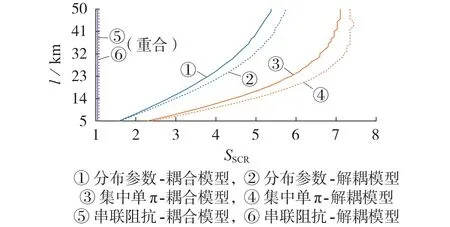
图4 不同l及SSCR下，dq轴耦合／解耦和不同线路模型的系统稳定性Fig.4 Stability of dq axis coupling／decoupling and different line models under different values of l and SSCR

图4 中，不稳定边界线为是否稳定的临界曲线，曲线以左为不稳定区，以右为稳定区。由图4可知：

1）当采用线路分布参数模型时，是否考虑dq轴耦合系统的稳定性判定结果趋势大体一致，但是在曲线①、②之间的系统运行点，实际系统是稳定的，忽略dq轴耦合判定结果为不稳定，将造成误判；

2）当采用线路集中单π 模型时，与线路分布参数模型对比，在曲线①、③之间的系统运行点，实际系统是稳定的，而采用线路集中单π 模型则判定结果为不稳定，将造成误判；

3）当采用线路串联阻抗模型时，与线路分布参数模型对比，在曲线①、⑤之间的系统运行点，实际系统是不稳定的，而采用线路串联阻抗模型则判定结果为稳定，也将造成误判。

综上所述，dq轴耦合及线路分布参数对于谐波不稳定分析不可忽略，否则将导致无法准确判定系统稳定性。

4 仿真验证

为了验证本文理论分析的准确性，按照图2 所示拓扑结构，在MATLAB／Simulink 仿真环境中搭建分布式电站并网模型。设置2 种仿真场景，具体设置情况见附录E 表E1。进一步根据第3章的理论分析结果，场景1 和场景2 对应时段下SSCR的稳定性判定结果如表2所示。表中：“√”表示稳定；“×”表示不稳定；模型①—④分别为分布参数-耦合模型、分布参数-解耦模型、集中单π-耦合模型、串联阻抗-耦合模型。需注意的是，当SSCR=39.19（强电网）时2 种场景下系统均是稳定的。

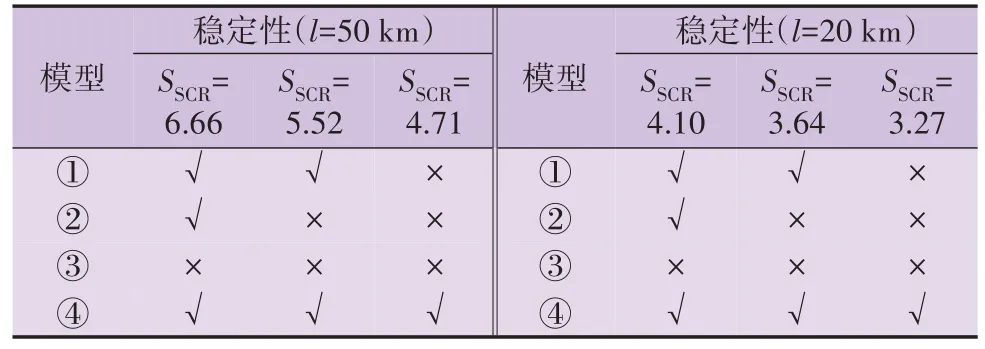
表2 场景1和场景2对应时段SSCR的稳定性Table 2 Stability of different under Scenario 1 and Scenario 2

仿真结果只需与同时计及dq轴耦合及线路分布参数时的理论分析结果一致，即可验证本文理论分析结果的准确性，同时也可说明忽略dq轴耦合或线路分布参数，将导致系统稳定性的误判。

图5 为2 种仿真场景下SSCR不同时Ipcc时域波形。由场景1 仿真结果可知：SSCR分别为39.19、6.66和5.52 时，电流波形良好；1.4 s 时SSCR降至4.71，电流发散；之后进入等幅振荡环节，波形质量严重恶化，系统不稳定。类似地，由场景2 仿真结果可知：当SSCR降至3.27 时，电流发散，系统不稳定。仿真结果验证了第3 章中同时计及dq轴耦合与线路分布参数模型时的稳定性理论分析结果（即当l=20 km、SSCR=3.27 与l=50 km、SSCR=4.71 时，系统不稳定），同时也证明了若忽略dq轴耦合或线路分布参数，将导致错误的系统稳定性判定结果。

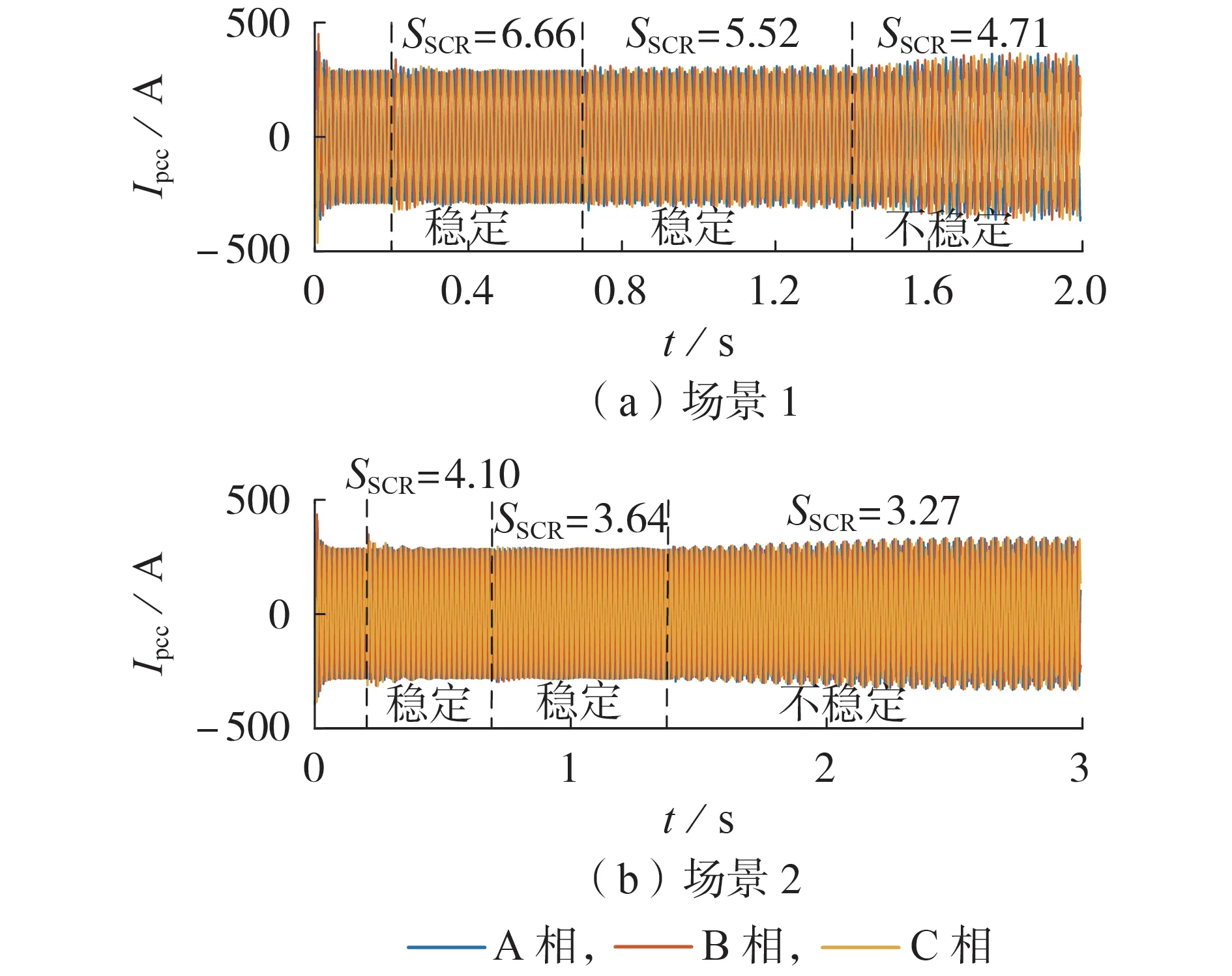
图5 2种场景下PCC处电流Ipcc时域波形Fig.5 Time domain waveforms of Ipcc in two scenarios

对图5 中各稳定时段（即［0，0.2）、［0.2，0.7）、［0.7，1.4］ s 内时域波形进行傅里叶分解，可得各时段内谐波频谱，如附录E 图E3 所示。而基于本文所提方法理论分析得到的不同场景下的潜在谐波放大频率如附录E 表E2 所示。需注意的是，此处谐波放大频率是LTF的奈奎斯特曲线与单位圆交点所得的截止频率。

对比图E3 中频谱尖峰点及表E2 中截止频率点的匹配度，可验证所得潜在谐波放大点的准确性，具体如下。

1）当线路采用集中单π 模型时，较低频次截止频率点与频谱尖峰点一致；较高频次截止频率点与频谱尖峰不一致，且出现有高频频谱尖峰点而无高频截止频率点现象。证明采用线路集中单π模型仅能分析较低频次谐波放大点，而无法准确分析到较高频次谐波放大点，甚至会遗漏高频谐波放大点。

2）当线路采用串联阻抗模型时，理论分析所得截止频率与频谱尖峰没有直接对应关系，完全无法准确分析系统潜在谐波放大点。

3）2 种场景下，唯有线路采用分布参数模型时，不同SSCR下谐波电流频谱尖峰与理论分析截止频率结果基本都一致。证明了截止频率处存在潜在谐波放大风险，同时也验证了本文分析所得系统潜在谐波放大点的准确性。进一步分析表E2数据可知，系统稳定前提下，是否考虑dq轴耦合对于分析潜在谐波放大点影响不大，均可准确分析出系统所有潜在谐波放大点。

5 结论

本文针对同时计及dq轴耦合和线路分布参数的分布式电站系统极点分布难以求解问题，提出基于GNC 的系统超越方程极点分布间接判定方法，给出复杂闭环传递函数矩阵的回率矩阵和稳定条件判定详细步骤，并分析了不同线路长度和电网强度下，dq轴耦合和线路分布参数对系统谐波不稳定的影响。研究表明，所提方法可准确分析同时计及dq轴耦合和线路分布参数的分布式电站谐波不稳定问题，且dq轴耦合或线路分布参数因素对系统稳定性的影响不可忽略，尤其是线路分布参数特性对高频谐波放大点的影响不可忽略。

附录见本刊网络版（http：//www.epae.cn）。