直流偏磁对500 kV变压器振动特性的影响分析

何 良，吴天宝，李 荣，丁登伟，杨 洁，李盛涛

（1.清华四川能源互联网研究院，四川 成都 610213；2.国网四川省电力公司电力科学研究院，四川 成都 610072；3.成都航空职业技术学院，四川 成都 610100；4.西安交通大学 电气工程学院，陕西 西安 710049）

0 引言

特高压直流输电工程作为能源传输的骨干网络，在构建新型电力系统、服务“双碳”目标中发挥着重要作用。“ 十四五”期间，国家电网公司将继续加快特高压直流工程建设，完善特高压骨干网架。随着直流工程不断发展，直流偏磁问题愈发突出。当特高压直流工程单极-大地回路运行时，数kA 的直流电流通过接地极流入大地，致使部分直流电流侵入大型电力变压器绕组，最高电流幅值达200 A，产生直流偏磁现象，引发变压器损耗增加、振动噪声加剧、局部过热等不良后果，严重影响变压器的安全稳定运行［1］。振动监测法具有灵敏度高、与系统无直接电气连接、易于实现带电检测等诸多优点，近年来在变压器机械状态检测及诊断中逐渐引起国内外学者的关注［2］。变压器运行时的振动主要来源于铁心和绕组，在直流偏磁作用下，变压器励磁电流畸变，铁心磁致伸缩特性发生改变，漏磁增加，导致铁心和绕组振动异常，故开展直流偏磁下变压器振动特性的研究有助于变压器状态评估［3⁃4］。

目前，国内外学者对变压器直流偏磁振动开展了若干研究。文献［5⁃6］研究了直流偏磁对硅钢片磁致伸缩特性的影响，指出直流偏磁使磁致伸缩回环失去原有的对称性，偏磁磁场使磁致伸缩峰值增大，形变加剧，但研究仅限于硅钢片层面。文献［7⁃10］分析了直流偏磁对变压器的振动特性的影响，并开展了相关试验研究，但研究仅限于低电压、小容量变压器。然而，有关高电压、大容量变压器直流偏磁的振动研究还相对较少，仅文献［11⁃12］分析了500 kV 单相变压器的振动特性，通过频谱分析得到一些重要结论。综上所述，直流偏磁对大型变压器振动特性影响的研究还存在诸多不足，尤其是电网中具有相当比例的大型三相变压器。

本文依托白鹤滩 — 江苏±800 kV 特高压直流输电工程（简称白鹤滩 — 江苏工程），开展直流偏磁对大型变压器振动特性影响的研究，详细分析了变压器的振动机理及直流偏磁对变压器振动的影响机制；在白鹤滩 — 江苏工程调试期间，对500 kV 三相变压器的中性点电流、振动信号进行了测量；量化了直流偏磁程度，分析了不同直流偏磁程度下变压器振动信号时域及频谱特征，提取了典型特征量分析直流偏磁程度对变压器振动特性的影响，为大型变压器直流偏磁下的振动机制及特性研究提供参考。

1 变压器的振动机制

1.1 铁心的振动机制

铁心振动主要由硅钢片的磁致伸缩以及硅钢片间的电磁力引起，且磁致伸缩是主要原因［13］。变压器正常运行时，假定铁心磁通量φ为：

式中：φa为交流磁通幅值；ω为电源角频率。

铁心中磁感应强度B为：

式中：S为铁心横截面积。

在一定范围内，铁心磁致伸缩位移量λ近似正比于φ2，满足如下关系：

式中：L为硅钢片轴向尺寸；εs为硅钢片饱和磁致伸缩率；Bs为硅钢片饱和磁感应强度。

综上可得，由磁致伸缩引起的铁心振动加速度ac为：

可以看出，铁心振动基频为2 倍电源频率。由于铁心材料具有非线性特性，铁心振动信号中除基频100 Hz 分量外，还含有谐波分量，如200、300 Hz等100 Hz的倍频分量。

1.2 绕组的振动机制

当变压器绕组中流过负载电流时，在交变的漏磁场作用下产生周期性的振动［14］。变压器正常运行时，假定负载电流I为：

式中：Im为负载电流幅值；ϕ0为电流初始相角。

漏磁场中磁感应强度Bw正比于负载电流，满足如下关系：

式中：Kb为比例系数。

作用在绕组线圈上的电磁力F为：

绕组振动是电磁力激励下的强迫振动，满足如下方程：

式中：M为绕组模型质量矩阵；C为模型阻尼系数矩阵；K为模型弹性系数矩阵；z为线圈的静态位移矩阵；F为洛仑兹力矩阵；g为加速度。

综上可得，由电磁力引起的绕组振动加速度aw为：

式中：A和α与初始条件相关；D和β为固定条件下与绕组参数有关的常数。

可以看出，绕组振动基频为2 倍电源频率。由于垫块等绝缘材料的非线性动力学特性，绕组振动信号中除基频100 Hz 分量外，还存在200、300 Hz 等谐波分量。

1.3 直流偏磁下变压器的振动机制

直流偏磁产生机理和铁心磁通与磁致伸缩位移的对应关系分别如附录A图A1、A2所示。

变压器正常运行时，工作在铁心磁化曲线线性段。当绕组中流过直流电流时，铁心中直流磁通φd与交流磁通φacos(ωt)相叠加，致使总磁通曲线整体向上偏移，如附录A 图A1（a）所示；这使得原来处于线性段的部分磁化曲线偏移至饱和段，导致与直流磁通同向的半周期磁感应强度增大，而反向的半周期磁感应强度减小，如附录A 图A1（b）所示；进而导致励磁电流发生畸变，形成正负半周期不对称的尖波，变压器工作在半周期饱和状态，如附录A 图A1（c）所示。这导致铁心磁导率下降，漏磁增加，励磁电流与谐波分量增大，加剧了绕组振动［15］。

另一方面，变压器正常运行时，磁致伸缩位移量λ是变形的正弦信号，正负半周期近似对称，如附录A 图A2（c）中的实线所示。当变压器存在直流偏磁时，铁心磁通量φ是在交变磁通φacos(ωt)上叠加了直流磁通φd，由于铁心磁致伸缩位移是磁通的函数［13］，直流偏磁时磁致伸缩位移与磁通间的近似关系如附录A 图A2（c）中的虚线所示，在磁通正半周期磁致伸缩位移幅值增大、铁心形变加剧，负半周期对应的位移及变形变较小，这导致正负半周期波形不再对称，信号复杂度增加［11］。

2 大型变压器直流偏磁现场测试

白鹤滩—江苏工程是“西电东送”重点工程，额定输送功率达8 000 MW，额定电流为5 000 A。布拖换流站是该工程送端站，大坝接地极与换流站直线距离约为25 km。布拖换流站周边部分变电站及直流接地极的拓扑结构如附录A图A3所示。

500 kV普提变电站与大坝接地极间直线距离约为17.1 km，站内2 号500 kV 主变基本信息如附录A表A1 所示。系统调试时2 号主变中性点直接接地，高压侧、中压测和低压侧负载电流分别为450、1 020、930 A。

白鹤滩—江苏工程进行单极-大地回路调试时，设置系统调试电流为500、1 000、1 500、2 000 A这4种工况。在调试前和上述4种工况下，分别检测500 kV普提变电站2 号主变中性点电流和振动信号。4 个典型振动测点分别布置在高压套管侧、中压套管侧油箱壁下1/3 处，如附录A 图A4 所示。振动检测系统为自主研制，振动传感器型号为PCB 333B50，频带范围为0.5～3 000 Hz，灵敏度为1 000 mV／g，系统每秒采样25 600点。

3 测试数据分析

3.1 直流偏磁程度量化

白鹤滩—江苏工程进行调试时，2 号主变中性点电流与系统调试电流呈线性增长关系，如图1 所示。当系统未调试时中性点电流为0，当系统调试电流为2 000 A 时中性点电流增加至10.6 A，表明存在明显的直流电流id侵入2号主变绕组。

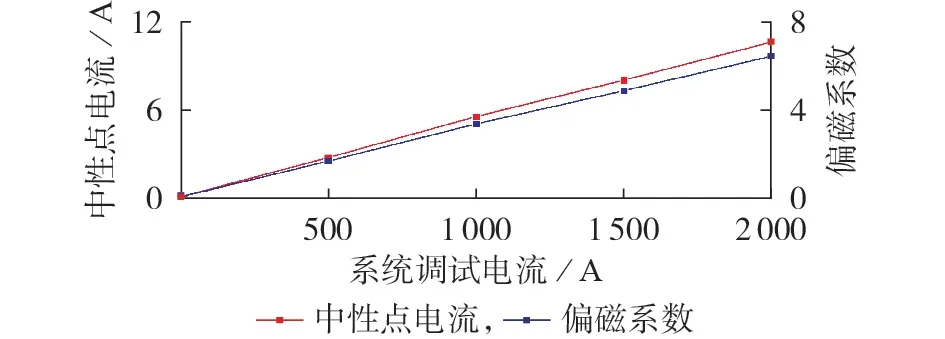
图1 中性点电流及偏磁系数与系统调试电流的关系Fig.1 Relationship between neutral current，DC bias coefficient and system debug current

直流电流id使铁心中产生相应的直流磁通φd，φd能直接反映直流偏磁水平。而φd往往不能直接测得，若要准确计算φd，则不仅需要考虑铁心磁滞效应，还需要对模型中的基本磁化曲线进行反复迭代修正，算法复杂。但若直接采用id描述直流偏磁程度，又未考虑到变压器本身的实际情况。因此，从工程实用的角度出发，本文基于励磁电流ie与直流电流id定义偏磁系数，以量化直流偏磁程度，具体如下：

式中：k为偏磁系数。

由2 号主变铭牌参数可得，高压绕组的励磁电流ie=0.55 A，文献［16］报道了直流电流在变压器绕组中的分布情况，为简化分析，本文假定id在三相中平均分配。调试期间，2 号主变直流偏磁程度如图1所示，其变化趋势与中性点电流一致。

3.2 振动信号时域波形分析

系统调试期间，2号主变测点1振动信号的时域波形变化如图2 所示，其他测点振动信号的时域波形变化见附录A 图A5 — A7。当无直流偏磁时，4 个测点振动信号存在差异性，但均为变形的正弦波形，1 个励磁周期内2 个半周期对应的振动波形高度相似，呈对称分布。当变压器中性点注入直流时，变压器工作在半周期饱和状态，4 个测点振动信号畸变明显，信号复杂度增加，不再近似正弦波形，2个半周期对应的信号波形相似度降低，不再对称分布。随着偏磁系数的增大，4个测点振动信号畸变增大。

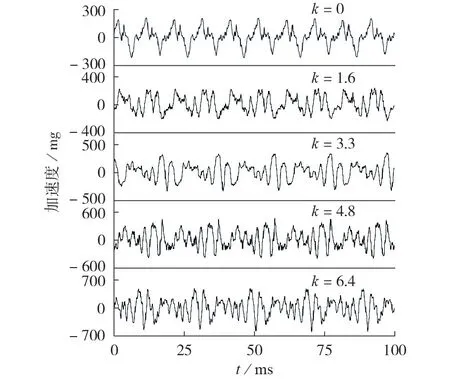
图2 测点1在不同偏磁系数下的振动信号Fig.2 Vibration signal at Point 1 under different DC bias coefficients

2 号主变4 个测点加速度有效值变化趋势如附录A 图A8所示。由图可见：加速度有效值整体随直流偏磁呈增大趋势；受变压器结构影响，不同测点的加速度有效值变化趋势存在差异性，其中测点2 受影响最大，加速度有效值从无直流偏磁时的105 mg增加至偏磁系数为6.4时的346 mg。

3.3 振动信号频谱分析

系统调试期间，2号主变测点1振动信号的频谱分布变化如图3 所示，其他测点振动信号的频谱分布变化见附录A 图A9 — A11。当无直流偏磁时，测点1 振动信号的频率主要分布在100、300、500 Hz处，测点2、3振动信号的频率主要分布在100、300 Hz处，测点4振动信号的频率主要集中在100 Hz。不同测点振动信号频谱分布不同，但主频均为100 Hz。

图3 测点1在不同偏磁系数下的信号频谱Fig.3 Frequency spectra of signal at Point 1 under different DC bias coefficients

当变压器中性点注入直流时，振动信号中50 Hz奇次谐波分量明显增多，例如当k=1.6 时，测点1 出现了450、550 Hz等分量，测点2 出现了250 Hz分量，测点3、4 均出现了250、350、450 Hz 等分量。随着偏磁系数逐渐增大，不同测点谐波分量变化存在差异性，主频分量也发生变化，如当k=6.4 时，4 个测点的主频分量分别为250、250、350、450 Hz。此外，随着偏磁系数增大，50 Hz 倍频分量幅值增加各异，信号能量主要集中在600 Hz以内。

4 直流偏磁对变压器振动特性影响分析

正常情况下，变压器振动信号近似变形的正弦波形，而直流偏磁导致波形发生畸变。直流偏磁对振动信号100 Hz基频分量的影响如图4所示。测点1、2、4 处的100 Hz 基频分量受直流偏磁影响并不明显；而测点3 处的100 Hz 基频分量整体呈减小趋势，从无直流偏磁时的146 mg 减小至偏磁系数为6.4 时的78 mg。由此可见，直流偏磁导致信号畸变及振动加剧的本质原因在于除基频分量外的50 Hz倍频分量显著增多。

为描述直流偏磁对波形畸变程度的影响，提取50 Hz 倍频谐波分量与100 Hz 基频分量的能量比，即波形畸变比作为第1 个特征值。由于变压器振动信号频谱主要分布在2 kHz 以内，本文仅对2 kHz 以内的振动信号进行分析。波形畸变比RTHD的计算公式如式（11）所示。

式中：Ai为第i个50 Hz 倍频谐波分量的幅值；A2为100 Hz 基频分量幅值；N为2 kHz 频率范围内50 Hz倍频谐波分量个数。

各测点波形畸变比变化趋势如图5 所示。由图可见：无直流偏磁时各测点波形畸变比均小于0.5，振动信号以基频分量为主；随着偏磁系数增大，各测点波形畸变比变化存在差异性，但整体呈增大趋势；测点4 的波形畸变相对较小，当偏磁系数为6.4 时波形畸变比为7；测点3 的波形畸变最大，当偏磁系数为6.4时波形畸变比增大至28。

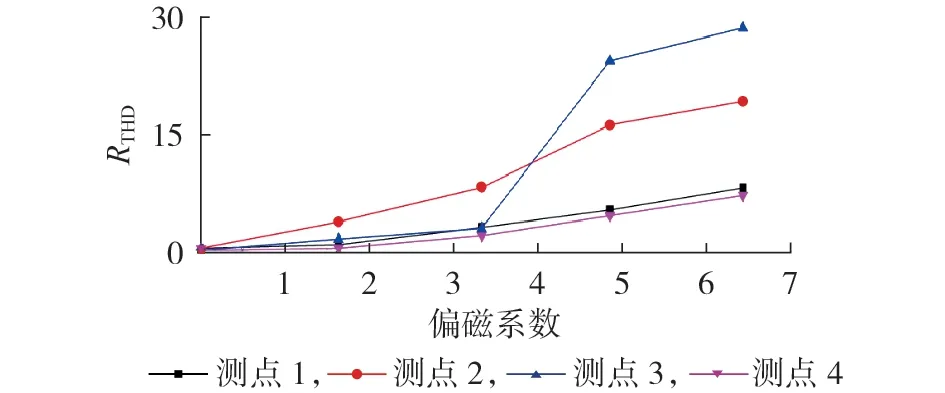
图5 振动信号波形畸变比变化趋势Fig.5 Change trend of waveform distortion ratio of vibration signal

同时，为分析直流偏磁对50 Hz 奇次、偶次谐波的影响，提取2 kHz 频段内50 Hz 奇偶次谐波能量比Ro/e作为第2个特征值，其计算公式如式（12）所示。

式中：A2i-1、A2i分别为50 Hz奇次、偶次谐波幅值。

各测点的Ro/e变化趋势如图6 所示。由图可见：无直流偏磁时，各测点的Ro/e趋近于0，振动信号以50 Hz 偶次谐波分量为主；随着偏磁系数的增大，各测点的Ro/e变化存在差异性，但整体呈增大趋势；测点3 处的Ro/e变化最明显，当偏磁系数为6.4 时Ro/e增大至4.3；测点4 处的Ro/e变化相对较小，当偏磁系数为6.4 时Ro/e增大至1.4；直流偏磁会同时导致50 Hz奇次、偶次谐波分量增多，但奇次谐波增幅大于偶次谐波。

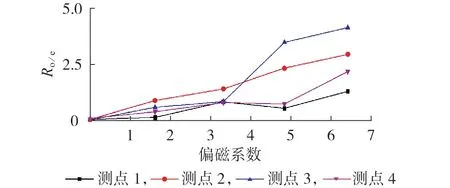
图6 振动信号奇偶次谐波能量比变化趋势Fig.6 Change trend of energy ratio between odd harmonics and even harmonics of vibration signal

进一步地，为分析直流偏磁对50 Hz 倍频谐波分量在频带内分布的影响，提取累计能量占比Rl/a作为第3个特征值，具体如式（13）所示。

式中：Nthres为截止频率内50 Hz倍频谐波分量个数。

各测点的Rl/a变化趋势如附录A 图A12 所示。由图可见：无直流偏磁时，4 个测点的振动信号能量主要集中在300 Hz以内，占比分别为0.91、0.96、0.96和0.94；随着偏磁系数的增大，各测点的能量分布变化显著，曲线台阶变多，50 Hz 奇次谐波梯度大于偶次谐波，600 Hz 后曲线变缓，逐渐趋于稳定；当偏磁系数为6.4 时，4 个测点的600 Hz 内能量占比分别为0.93、0.96、0.91 和0.91，上述结果表明直流偏磁导致增加的50 Hz倍频谐波主要集中600 Hz以内。

更进一步地，为分析直流偏磁对50 Hz 倍频谐波分量在频带内变化规律的影响，提取功率谱熵H作为第4个特征值，H的计算公式如式（14）所示。

各测点功率谱熵H变化趋势如图7 所示。由图可见：各测点H存在差异，但整体变化趋势相似，当偏磁系数较小时，H逐渐变大，但偏磁系数增加到一定程度后，H不再增加，且略有下降。这是由于铁心饱和作用，直流偏磁增大到一定程度时，磁不平衡性降低，振动信号复杂度不再增加。

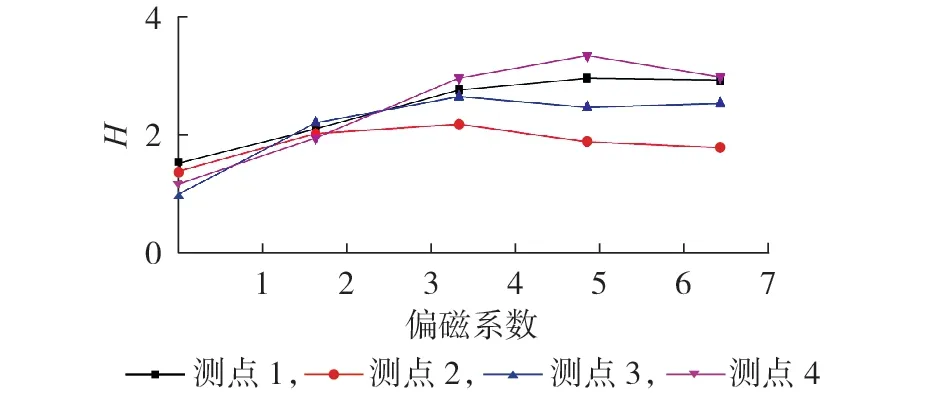
图7 振动信号功率谱熵变化趋势Fig.7 Change trend of entropy power spectrum of vibration signal

5 结论

本文分析了变压器的振动机理及直流偏磁影响机制，在白鹤滩—江苏工程调试期间，对500 kV 三相变压器的中性点电流、振动信号进行了实测，量化了直流偏磁程度，开展了振动信号时域和频域分析，通过提取波形畸变比、奇偶次谐波能量比、高低频能量比、功率谱熵等特征量分析了直流偏磁对变压器振动特性的影响机制，得到以下结论。

1）变压器正常运行时，工作在铁心磁化曲线线性段，振动信号基频为2 倍电源频率。直流偏磁使部分铁心磁化曲线偏移至饱和段，励磁电流和磁致伸缩位移发生畸变，进而影响变压器振动特性。

2）当直流电流侵入大型变压器时，振动信号畸变明显，复杂度增加，不再近似正弦波形，2 个半周期对应的信号波形相似度降低，不再对称分布。随着偏磁程度增加，振动信号主频分量发生改变，频谱中50 Hz 奇次倍频谐波分量明显增多，不同测点各谐波分量幅值增加各异。

3）直流偏磁对变压器振动的影响机制在于除基频分量之外的50 Hz 倍频谐波分量显著增多，其中50 Hz奇次谐波增幅要大于偶次谐波，且影响主要集中在600 Hz 以内。由于铁心饱和作用，直流偏磁增大到一定程度时，磁不平衡性降低，振动信号复杂度不再增加。

附录见本刊网络版（http：//www.epae.cn）。