基于混合优化算法的多目标装配线平衡问题求解模型

李俊成 王 巍

（东北林业大学机电工程学院，黑龙江 哈尔滨 150040）

装配线问题（Assembly Line Balancing Problem，ALBP）[1]在现代制造领域中具有重要地位，自福特汽车公司建立生产线以来，相关人员一直在探索和研究该问题，并在此期间进行了多次尝试。

装配线平衡问题的不同的目标函数主要分为3 类：在已知生产节拍的情况下，使工作站数最小化（即ALBP-Ⅰ）；在已知工作站数的情况下，使生产节拍最小化（即ALBP-Ⅱ）；在已知工作站数和生产节拍的情况下，使装配线负荷更均匀，即平滑指数最小化（即ALBP-Ⅲ）。已知装配线问题属于NPhard 问题[2]，通常使用精确算法或元启发式算法对装配线平衡问题进行求解，例如原丕业等[3]提出的改进的自适应遗传算法求解模型能够更好地解决混流装配线平衡问题。

本文根据装配线平衡问题的特征，以最小化工作站数量、综合考虑装配线平衡率和平滑指数为优化目标建立装配线平衡模型，并结合遗传算法与蚁群算法，提出了一种混合优化算法模型（GA-ACO），以解决装配线平衡问题。

1 装配线平衡模型构建

本文研究的装配线平衡问题是在生产节拍已知的情况下，在装配过程中，各工序在紧前作业顺序的约束下将全部工序安排到工作站中进行装配作业，保证每个工作站的装配时间不超过生产节拍，并尽量使安排的工作站数最少且每个工作站的装配作业时间和装配作业负荷尽量均衡。本文将装配线平衡率和平滑指数作为评价指标，其中的装配线平衡率表示装配线的平衡状况，平衡率越大，说明装配线平衡效果越好。平滑指标表示装配线的负荷状况，平滑指数越小，说明装配线负荷越均匀。本文将装配线平衡率与平滑指数相结合，并作为目标函数。

1.1 假设

本文所提问题的基本假设如下。1）只对某一类产品进行装配作业。2）每道工序作业时间是已知且确定的。3）所有作业工序必须满足优先顺序。4）每道工序只能分配到一个工作站中。5）每个工作站的装配工作时间不能超过生产节拍。

1.2 数学模型

本文所提多目标装配线平衡问题的数学描述如下。

装配线平衡率P越大，表示装配线平衡状况越好，即装配线空余时间最少；平滑指数SI越小，表示装配线负荷越均匀。二者分别如公式（1）、公式（2）所示。

式中：P为装配线平衡率；SI为平滑指数；m为工位的数量；sti为第i个工作站的工作时间；CT为生产节拍。

装配线平衡优化目标函数H1、H2分别如公式（3）、公式（4）所示。

约束条件如公式（5）～公式（8）所示。任意2 个工作站不能出现重复的工序如公式（5）所示。任意1 个工作站的装配时间都≦生产节拍如公式（6）所示。任意1 个装配工序都应被分配到工作站中如公式（7）所示。每个工序的紧前作业关系如公式（8）所示。

式中：H1、H2表示目标函数；Mk1、Mk2分别为第k1个和第k2个工作站所分配工序的集合；Tk表示第k个工作站的所有工序装配时间；M 表示所有工作站中工序的集合；Mk表示第k个工作站上所分配工序的集合；Pij=1 表示工序i是工序j的紧前作业顺序；i∈Ma、j∈Mb表示工序i和工序j分别在第a个和第b个工作站完成。

2 混合优化算法求解

2.1 混合算法设计

本文将遗传算法与蚁群算法相结合，提出了一种混合优化算法模型来求解装配线平衡问题。首先，对遗传算法参数进行初始化设置，用随机拓扑法[4]按照工序顺序图生成初始序列，产生初始种群，然后计算初始种群的适应度值。其次，通过选择、交叉和变异等方法生成新的种群，再计算新种群的适应度值。进行迭代调整后，得出最优结果。再次，将蚁群算法中所有参数进行初始化设置，将遗传算法得到的最终解作为蚁群算法最初的信息素分布，随机生成蚂蚁的初始节点，根据概率选择公式选择下一可行节点，更新信息素，并计算每条路径的信息素浓度。经过迭代调整后，生成装配线平衡问题的最优解。混合优化算法模型求解装配线平衡问题流程如图1所示。

图1 混合优化算法模型流程图

2.2 遗传算法设计

2.2.1 生成初始种群

本文要求初始群体中的所有作业序列均为可行作业序列，采用基于作业顺序的染色体编码规则。根据作业顺序图，用随机拓扑排序法生成初始序列，以确保初始种群的多样性。随机拓扑排序的一般步骤如下。1）从序列图中随机选择一个输入度为0 的顶点并输出。2）从序列图中删除该顶点和所有以该顶点为起点的有向线段。3）重复步骤1 和2，直到序列图为空或者不存在输入度为0 的顶点为止。4）输出当前序列并生成初始种群

2.2.2 选择

本文采用轮盘赌法进行选择操作。个体的适应度值越高时，则个体被选中的概率越大，如公式（9）所示。

式中：Pxi表示个体被选中的概率；fxi表示被选中个体的适应度值；fxj表示不同个体的适应度值。

2.2.3 交叉

交叉是指从种群中根据概率随机选择2 个个体，并将2 个个体间的染色体进行交换。本文选择的交叉方式是两点交叉，即从染色体中随机选择2 个交叉点，将这2 个交叉点间的染色体进行交换，形成新的基因序列，如图2所示。

图2 交叉操作示意图

2.2.4 变异

变异是指用其他等位基因替换个体染色体的基因座的基因值，从而形成一个新的个体，如图3所示。

图3 变异操作示意图

2.3 蚁群算法设计

2.3.1 评价解的质量的目标函数

本文求解的是ALBP-Ⅰ问题，即明确生产节拍，使工作站数最少。在求解过程中，如果以目标函数H1为目标函数，会出现大量重复解，不易区分。因此，选用目标函数H2来评价解的质量。

2.3.2 信息素更新

本文的信息素更新策略为全局信息素更新。当蚂蚁周游全部装配工序并构建全局最优解后，才会添加信息素，从而使其他蚂蚁跟随，提高了搜索的目的性。当前迭代中，全局最优蚂蚁会根据公式（10）、公式（11）更新全局信息素。

式中：τij为信息素强度；τij（t）为t时刻信息素强度；τij（t+1）为（t+1）时刻的信息素强度；ρ为信息素挥发系数；H2为当前最优分配方案的目标函数。

3 案例分析

基于上述算法的思路和流程，为了验证其有效性，用MATLAB R2021b 实现上述算法，采用网址“https：//assemblyline-balancing.de/”中的标准算例进行测试和比较。分别用传统遗传算法模型与混合优化算法模型对装配线平衡问题进行求解，并比较其平衡优化效果。

3.1 参数设置

本文采用经典问题Buxey 问题对模型进行验证，并与实例库中的其他案例[5-8]进行比较。Buxey 问题的作业优先顺序如图4所示。

图4 Buxey 问题的作业优先顺序图

基于混合算法求解装配线平衡问题，具体参数见表1。

表1 混合优化算法模型参数

3.2 实例结果分析

Buxey 问题由29 个装配工序组成，当生产节拍CT=36s 时，混合算法模型所得装配线平衡结果如图5所示。

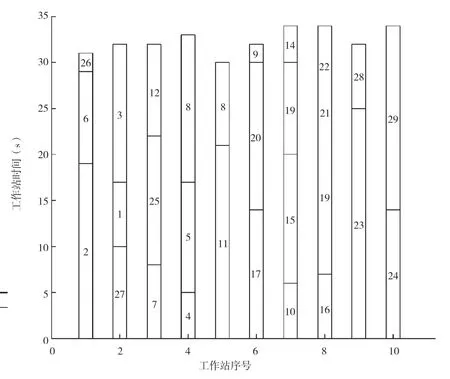
图5 装配线平衡图

本文将混合算法模型与传统遗传算法模型所得结果进行比较，见表2 和表3。根据表2、表3 可知，当混合算法模型和遗传算法模型在CT=36s 时，对于Buxey 问题，2 种算法模型都可以得出最小工作站数m=10 的结果，均为最优工作站数。但混合算法模型所得装配线平衡率和平滑指数分别为0.952941%和2.04939，而遗传算法模型所得装配线平衡率和平滑指数分别为0.925714%和4.09878。显而易见，混合算法模型所得装配线平衡率更高且平滑指数更小，证明在装配线平衡问题的求解方面，本文所提混合算法模型比遗传算法模型更好。

表2 混合算法模型求解结果

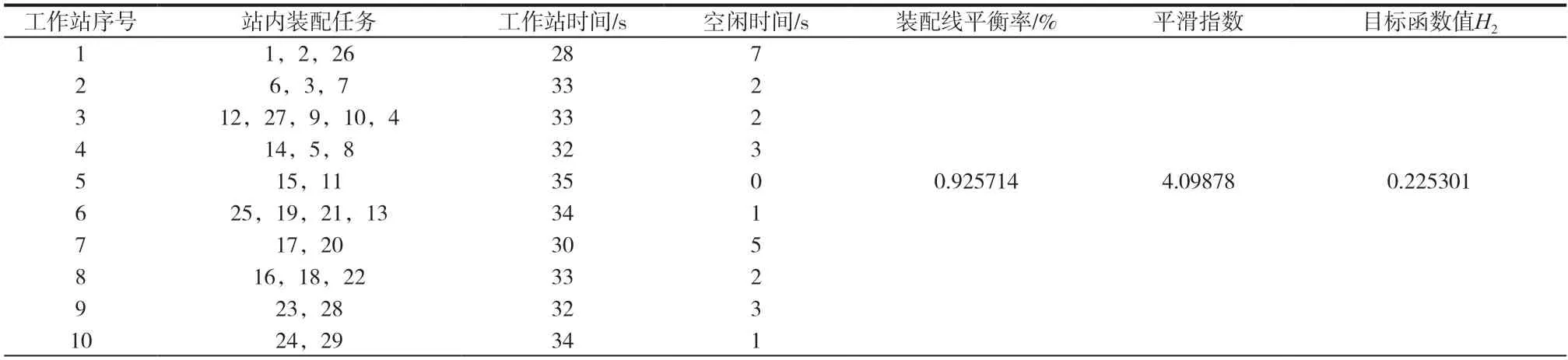
表3 遗传算法模型求解结果

为了更好地验证本文混合算法模型的有效性，需要与文献[5-8]中相同的经典案例进行比较，验证结果见表4。根据表4 可知，混合优化算法模型求解装配线平衡算例与遗传算法模型有较明显的差距。混合优化算法模型在每个算例的验证中都得到了最优工作站数，而遗传算法模型则在多种算例中多次出现未达到最优工作站数的情况。并且在2 种算法模型均达到最优工作站数的情况下，混合优化算法模型的目标函数值H2均不小于遗传算法模型的目标函数值H2。因此在装配线问题的求解中，本文提出的混合优化算法模型比遗传算法模型更具有效性。

表4 经典算例验证结果

4 结论

本文针对第一类装配线平衡问题，并结合第三类装配线问题提出了一种混合算法模型，在已知生产节拍的情况下，求解出最小工作站数、最大装配线平衡率和最小平滑指数。该算法模型将遗传算法与蚁群算法相结合，并以将遗传算法最终解作为蚁群算法最初信息素分布的方式将2 种算法结合起来，从而有效改进前期收敛速度不足的问题。在目标函数上，增加了装配线平衡率与平滑指数相结合的目标函数，能够在2 种算法同时获得最小工作站数的情况下更好地评价算法的优劣，进而选择效果更好的算法。与经典算例进行比较后可知，在求解装配线平衡问题方面，本文所提混合优化算法模型能够获得更多的最优解和最小的平滑指数。由此可以证明，本文所提GA-ACO 混合优化算法模型对装配线平衡问题具有更好的求解能力。