一种能量双向流动的PMSM控制策略研究

熊 博 张东青 孙成国

（黑龙江科技大学电气与控制工程学院，黑龙江 哈尔滨 150022）

随着全球能源的枯竭，国家进一步加强关于节能减排、能源再利用方面的工作，发布了一系列政策和措施。电机作为能源消耗的重要部分，有效利用电机的能量对节能减排有很重大的意义[1]。传统的电机驱动系统，网侧使用的是不可控整流装置，该控制方式虽然稳定可靠，但是会产生大量谐波污染电网且能量只能从电网流向电机，只能实现能量的单向流动，当电机处于制动或发电状态时，能量不能回馈给电网，造成浪费[2]。而双PWM 变换器将网侧的不可控整流装置替换为与机侧控制系统相同的PWM 变换器，如此一来，就可以实现能量从电网流向电机以及由电机流向电网的双向流动，且可以实现直流母线电压的可调节，具有电压波动小、能够减少网侧谐波和功率因数高的优点[3]。本文针对双PWM 变换器的网侧和机侧分别采用了电压定向的矢量控制策略和id=0 的矢量控制策略，并对系统进行了仿真验证。

1 双PWM 变化器数学模型

双PWM 变换器拓扑结构的中前端是三相电网，然后经过PWM 整流器和母线电容，最终连接到PWM 逆变器和永磁同步电机。如图1所示。

图1 双PWM 变换器拓扑结构图

1.1 整流器的数学模型

为了便于PWM 整流器数学模型的建立，通常需要进行如下假设：1）电网电压为三相对称的纯正弦波电压。2）网侧滤波电感为线性电感，不会饱和。3）在某些简化分析中，可以忽略功率器件的开关损耗。

笔者先建立了三相PWM整流器在ABC坐标系下的数学模型，如公式（1）所示。

式中：uDC为母线电压；Lg、Rg分别为网侧滤波电感、电阻；ix=（a，b，c）、ex=（a，b，c）、Sx=（a，b，c）分别为网侧三相电流、电压、开关函数；RDC为母线上的电阻负载；C为母线电容。

将其经过Clarke 变换到αβ坐标系下，再经过Park 变换到dq坐标系下的数学模型，如公式（2）所示。

式中：ed、eq为网侧电压的dq分量；id、iq为网侧电流的dq分量；Sd、Sq为开关函数的dq分量；ω为电压旋转角频率。

1.2 永磁同步电机的数学模型

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）的数学模型与网侧数学模型类似，都是根据基尔霍夫定律在三相静止坐标系下建立的，并利用Clarke-Park 变换转换到两相静止坐标系与两相同步旋转坐标系下。

笔者建立了 ABC 三相静止坐标系下的数学模型。其中，定子电压方程如公式（3）所示。

式中：ψA、ψB、ψC为A、B、C 三相绕组的全磁链；uA、uB、uC为A、B、C 三相绕组的相电压；iA、iB、iC为A、B、C 三相绕组的相电流；RS为定子相电阻；p 为微分算子。

磁链方程，如公式（4）所示。

式中：ψfA、ψfB、ψfC分别为永磁励磁磁场交链A、B、C 三相绕组产生的磁链；Lx=（A，B，C）为三相绕组自感；Lxy=（x≠y，x，y=A，B，C）为三相绕组互感。

将其经过Clarke 变换到αβ坐标系下，再经过Park 变换到dq坐标系下的数学模型（电压方程、磁链方程以及电磁转矩方程），如公式（5）～公式（7）所示。

式中：ud、uq为dq两相旋转坐标系下定子电压分量；id、iq为dq两相旋转坐标系下定子电流分量；ψd、ψq为dq两相旋转坐标系下定子磁链分量；ωr为转子电角速度。

磁链方程如公式（6）所示。

dq的轴电感，如公式（7）所示。

式中：Ld、Lq分别为d轴和q轴电感；Lsσ为相绕组漏电感；Lmd、Lmd分别为直轴和交轴等效励磁电感。

电磁转矩方程如公式（8）所示。

由公式（3）～公式（8）可以看出，PMSM 在ABC轴系下的数学模型具有非线性、时变性以及耦合性的特点。在经过dq轴分解后，坐标系由三相静止坐标系变为两相正交旋转坐标系，消除了数学模型的耦合性和时变性，并消弱了非线性。通过解耦励磁分量和转矩分量，实现类似于他励直流电机的独立控制，对电流的控制实际上就是对dq电流矢量的控制。

2 双PWM 变换器的控制策略

2.1 网侧控制策略

PWM 整流器的控制如下：1）控制直流母线电压并降低电压纹波。2）实现单位功率因数运行，以降低损耗。3）降低电流谐波含量，提高电能质量。4）对有功功率与无功功率进行控制。

控制策略包括电流控制策略、并网控制策略以及其他控制策略[4]。

本文采用的是并网控制策略中常用的电压定向的矢量控制策略[5]，其控制框图如图2所示。

图2 电压定向的矢量控制策略

电压定向的矢量控制策略，根据Clarke 变换与Park变换，将三相静止坐标系下的物理量转换为两相旋转坐标系中，使直轴或交轴与电网合成电压矢量对齐，内环采用电流PI 控制器，外环采用电压PI 控制器实现无静差跟踪，利用SVPWM 或SPWM 调制方式驱动功率器件，参数设计与整定相对简单，因此可实现对有功和无功的独立控制[6]。

2.2 机侧控制策略

逆变器侧的控制对象是永磁同步电机，其控制策略是控制器的核心，对电机运行性能和效率有很大影响。电机的控制目标通常为实现位置、转速、力矩控制。当前常见的控制策略主要包括恒压频比控制、矢量控制、直接转矩控制[7]。

本文采用常用的矢量控制，其控制框图如图3所示。

图3 矢量控制

矢量控制（Vector Control，VC）于20世纪70年代提出，其目的是使交流电机获得与直流电机类似的控制特性。矢量控制基于检测到的交流电机的相电流与角位置，通过坐标变换将三相静止坐标系的物理量转换到两相旋转坐标系下，实现电机励磁与转矩之间的解耦，可分为转子磁场定向控制和定子磁场定向控制2 种。一般为转速电流双闭环的结构结合SVPWM 等调制技术实现电机调速。当前矢量控制主要研究结合模糊控制、自抗扰控制、滑模控制等非线性控制策略提升调速性能，针对减少成本与体积问题的无位置控制策略，解决高速情况下交直轴电流交叉耦合等问题。

3 仿真

3.1 仿真条件

根据上述理论，网侧采用电网电压定向的矢量控制，机侧采用矢量控制，实现机侧和网侧的独立控制和能量的双向流动。仿真条件如图4所示，包括空载启动、正转电动、反转电动、正转制动和反转制动5 个部分。转矩在在-10 N·m～+10 N·m进行阶跃变化，转速为-1 000 r/min～1 000 r/min，并采用斜坡过渡。

图4 电机四象限运行条件

网侧与机侧仿真参数见表1 和表2。

表1 网侧仿真参数

表2 机侧仿真参数

3.2 机侧仿真结果

电机在空载状态下启动，其转速能够良好地跟随设定值，当0.2 s 时，电机进入正转电动制动状态，由于负载突变较大，因此转速出现短暂提高的情况，但随后迅速稳定至设定值。电机之后的反转电动和反转制动过程与正转情况相似，均能够良好地跟随设定值。如图5所示。

图5 电机转速

电机在空载状态下启动，随着转速提高，电磁转矩也逐渐变大，当0.2 s 时，电机进入正转电动状态，其电磁转矩跟随设定值并基本稳定在约10 N·m。当0.4 s 时，电机进入正转制动状态，电磁转矩迅速下降至峰值约-12 N·m，然后迅速恢复至设定值约-10 N·m。电机之后的反转状态与正转状态相同，电磁转矩的变化情况也相同。如图6所示。

图6 电机转矩

q轴的电流变化曲线和电磁转矩一致，实现了对转矩的控制，d轴电流基本稳定在0，实现了id=0 矢量控制。如图7所示。

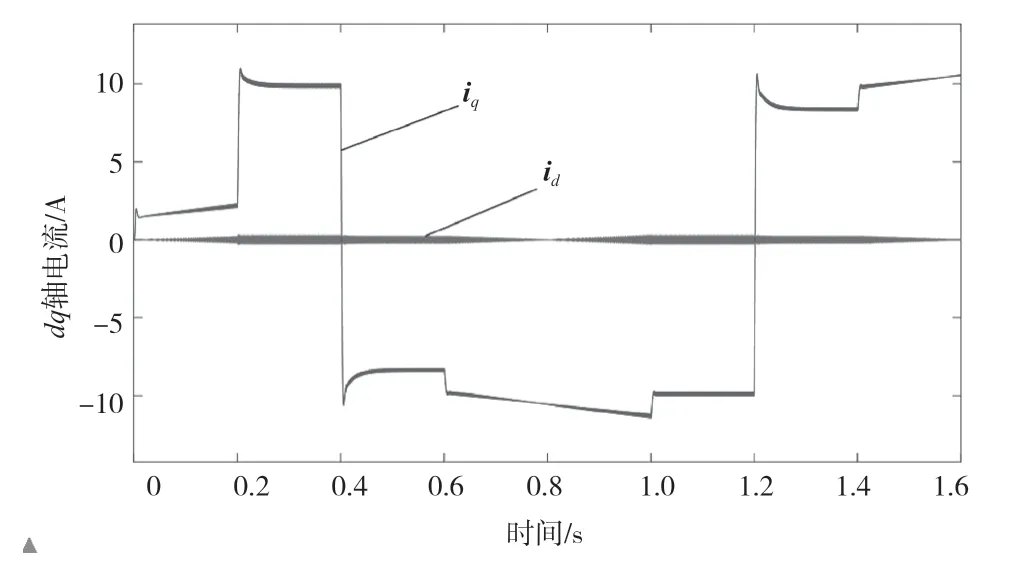
图7 dq 轴电流

随着电机转速的提高，有功功率也相应提高。当电磁转矩发生突变时，有功功率迅速提高并保持稳定。可以观察到，当电机处于电动状态时，有功功率为正，能量由电网流向电机。而当电机处于制动状态时，有功功率为负，能量由电机流向电网，体现了能量的双向流动特点。如图8所示。

图8 电机有功功率变化曲线

3.3 网侧仿真结果

当电机处于空载启动状态时，直流母线电压会迅速升高并且其响应速度很快，但也会存在超调的情况。随后，在0.2 s 内，电机将进入正转电动状态，导致负载突然增加，进而使母线电压下降。但是，电压会迅速恢复并稳定在给定的水平。0.4 s 电机进入正转制动，由于电机存在能量回馈，这部分能量缓冲在母线电容上，造成母线电压上升，之后又迅速恢复为给定。电机进入反转情况与正转类似。如图9所示。

图9 直流母线电压

4 结语

本文针对传统永磁同步电机控制策略能量利用率低的问题，采用了双PWM 变换器的控制策略，其中，对网侧采用了电网电压定向的矢量控制，而在机侧，则选用了常用的id=0 矢量控制。通过SVPWM 调制技术，提高了电压的利用率，并在MATLAB/SIMULINK 软件中对其进行了仿真验证。仿真结果表明，本文提出的控制策略能够实现网侧和机侧能量的双向流动，从而有效地减少了能量的损耗。此外，该策略还使网侧能够以单位功率运行且机侧控制性能良好，使其能够达到理论预期的运行状态。