灰色模型和ARIMA模型在专利授权数预测中的应用

杜彤彤

（天津商业大学，天津 300000）

我国知识产权事业不断发展，发明专利是知识产权的一种形式，作为技术创新信息的载体，发明专利的授权数量可以在一定程度上反应社会公众创新意识的程度，其中专利价值既包括对全社会知识存量贡献的社会价值，又包括其所创造的经济价值[1]，与地区发展之间有密切联系。地区发明专利的授权数量可以较好地衡量地区突破性技术创新水平，反映地区的综合实力[2]。本文运用ARIMA 模型和GM（1，1）模型对天津市发明专利的授权数量分别进行预测。通过本文的研究，为天津市出台加强知识产权保护政策提供参考，同时能加深对知识产权保护和成果转化的重视程度，在此基础上对天津市制定地区专利规划提出合理建议，具有重要的理论和现实意义。

1 理论依据

1.1 数据来源

本文为衡量天津市的综合创新能力，选取2003—2020年天津市发明专利的授权数量作为原始数据，共18 期数据，来预测2021年和2022年两年天津市发明专利的授权数量，数据均来源于天津市统计年鉴。

1.2 模型说明

1.2.1 ARIMA 模型

本文选择ARIMA 模型来建立预测模型。ARIMA 模型的全称是差分自回归移动平均（Auto-Regressive Integrated Moving Average）模型，其是由Box 和Jenkins 提出的时间序列预测方法，是一种精度较高的时间序列短期预测方法，目的是根据过去的行为对未来的行为进行预测。ARIMA 模型的基本思想是将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列，这个模型一旦被识别后就可以通过时间序列的过去值及现在值来预测未来值，在实际分析的过程中，对于不平稳的时间序列来说，经过d 次差分，转化为平稳序列后服从ARMA（p，q）模型，则称时间序列服从于ARIMA（p，d，q）模型，具体模型形式如公式（1）所示。

式中：yt为t年份的专利授权数取对数；φp为自相关系数；θq为滑动系数；εt-q为q阶误差值。

具体建模步骤如下：首先，判断序列的平稳性，如果数据非平稳，那么对原序列进行d 阶差分运算，使其转化为平稳序列。其次，根据时间序列的自相关系数（ACF）和偏自相关系数（PACF）识别参数p、q，拟合合适的ARMA模型。最后，检验模型参数是否显著，残差是否为白噪声序列，判断模型的拟合程度和有效性，并利用所拟合的模型对未来数据进行预测分析。

1.2.2 GM（1，1）模型

灰色预测是对含有已知和未知信息的系统进行预测，通过对系统因素之间的发展趋势进行关联分析，寻找其变化的规律，并对事物的发展趋势进行预测。主要特点是模型使用的不是原始数据序列，而是生成的数据序列。灰色预测所需的样本较少，且对于具有不确定性因素的复杂系统预测效果较好，GM（1，1）预测模型是其最常见的模型，常被用于经济预测分析。具体模型如公式（2）～公式（5）所示。

设原始序列：

通过一次累加生成新序列：

并做出X（1）的紧邻均值序列：

建立GM（1，1）模型：

式中：x（0）（k）为原始数据，即已知年份专利授权数；a为发展系数，它反映的是x（1）和x（0）之间的发展态势；b为灰作用量，它的大小反映数据变化之间的关系。z（1）（k）为通过一次累加生成新序列后的紧邻均值序列数据。

模型最小二乘估计满足公式（6）。

求解a，b后，得到GM（1，1）灰色微分方程的白化方程，如公式（7）所示。

其离散解，如公式（8）所示。

式中：a为发展系数，其反映x（1）与x（0）之间的发展态势；b为灰作用量，其大小反映数据变化之间的关系。

最终得到还原值，如公式（9）所示。

对得出的模型进行残差检验和后验查检验。

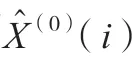
其次，计算其相对误差序列，如公式（12）和公式（13）所示。

最后，计算平均相对误差，如公式（14）所示。

平均相对误差值越小，说明模型的预测效果越好。使用后验差检验时，计算原始序列的标准差，如公式（15）所示。

式中：X（0）（i）为原始序列。

和绝对误差的标准差如公式（16）所示。

计算方差比，如公式（17）所示。

和小概率误差如公式（18）所示。

式中：S1为原始序列的标准差。

根据方差比和小概率误差的值对比后验查检验判别参照表判断模型的精度。

2 实证分析

2.1 ARIMA 模型预测

首先，检验原始时间序列是否具有平稳性，根据2003—2020年天津市发明专利的授权数量对数绘制专利授权数量对数随着年份变化的时序图，观察图中走势可以发现，专利授权书对数随着年份更迭呈现稳定增长的趋势。为精确地判断序列的平稳性，运用SPSS 软件对序列进行单位根检验，并选择适合的差分阶数对序列进行平稳化处理（见表1）。对数时序图如图1所示。

图1 专利授权数量对数时序图

表1 一阶差分序列ADF 检验结果

由检验结果可知，原始序列不能拒绝存在单位根的原假设，因此原始序列不平稳。对一阶差分序列检验的P＜0.05，因此拒绝原假设，一阶差分序列具有平稳性。通过观察一阶差分时序图的走势可以发现，在一阶差分时序图中的时间序列走势已经趋于平稳状态，观察表1 可知，0阶差分时的P值为0.265，1 阶差分时的P值为0.007，根据一阶差分序列ADF 的检验结果和时序图走势可以判断在一阶差分序列已经趋于平稳状态。因此，确定ARIMA（p，d，q）模型中d=1。根据一阶差分序列的自相关系数和偏自相关系数可确定模型中p和q的值。

一阶差分序列自相关系数和偏自相关系数见表2，由1-15 阶延迟的自相关系数变化趋势和偏自相关系数变化趋势可以看出偏自相关。函数表现为拖尾，自相关函数表现为一阶截尾，经过多次模型检验，并采取最小AIC 准则，最终本文选择的模型为ARIMA（0，1，1），模型参数估计见表3。

表2 一阶差分的自相关性

表3 模型参数估计

对模型残差进行白噪声检验，得出1-12 阶的AC值分别为0.001、-0.061、0.157、0.041、-0.073、0.113、0.081、-0.080、-0.234、0.139、-0.012、-0.084。

PAC值分别为0.001、-0.061、0.158，0.036、-0.056、0.097，0.062、-0.055，-0.263、0.114、-0.007、-0.004。

标准误差分别为0.00004，0.0796、0.6464、0.6883、0.8315，1.2059、1.4170、1.6473，3.8532、4.7385、4.7458、5.2007。

2-12 阶的p值分别为0.778、0.724、0.876，0.934、0.944、0.965、0.977、0.870、0.856、0.907、0.921。

可以看出各阶相关系数的p值＞0.05，说明残差为白噪声序列，原始序列中的有效信息已被充分提取。

根据表中模型参数估计的结果可知：C值为0.184358，MA（1）的值为0.744589，模型拟合公式如公式（19）所示。

式中：yt为预测值；εt-1为t-1 时刻的残差。

用模型对2019年和2020年天津市发明专利的授权数量进行预测，将得到的数据与实际数据进行对比，并利用该模型对2021年和2022年天津市发明专利的授权数量进行预测，得到的结果见表4。即通过ARIMA（0，1，1）模型预测的2019年和2020年天津市发明专利的授权数量的相对误差分别为0.08 和0.05。

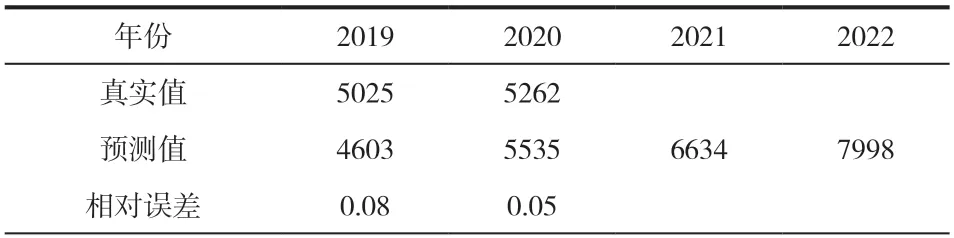
表4 模型ARIMA（0，1，1）预测值和预测误差

2.2 GM（1，1）模型的预测

GM 模型适应于小样本情况，为选择最佳数据维度，列举2013—2018年、2012—2018年及2011—2018年的数据对2019年和2020年的预测结果。选用后验查检验对模型进行检验和选择。其中，m为数据维度，c为模型方差比，p为小残差概率。根据预测结果并结合后验查检验判别参照表，选取m等于7 的GM（1，1）模型对2021年和2022年天津市发明专利的授权数量进行预测，所得到的预测数据见表5。通过GM（1，1）模型预测2019年天津市发明专利的授权数量2013—2018年、2012—2018年及2011—2018年的相对误差分别为0.17、0.06、0.08；2020年天津市发明专利的授权数量2013—2018年、2012—2018年及2011—2018年的相对误差分别为0.13、0.03、0.08。

表5 模型GM（1，1）预测值和预测误差

2.3 模型预测结果对比

从表6 可以看出ARIMA（0，1，1）模型和GM（1，1）模型预测的平均相对误差都较小，ARIMA（0，1，1）模型预测的平均相对误差为0.065，而GM（1，1）模型预测的平均相对误差为0.045。对于预测天津市发明专利的授权数量，GM（1，1）模型的预测结果更精准，更适用于小样本情况下的短期预测。

表6 模型预测结果对比

3 结论

利用GM（1，1）模型所预测2021年和2022年的预测值与实际值之间的平均相对误差＜5%，说明该模型的预测结果可靠，可以用该模型预测未来天津市发明专利授权数量的变化规律。通过ARIMA（0，1，1）模型和GM（1，1）模型的预测结果可知，天津市发明专利授权数量呈上升趋势，创新能力将进一步提高。地区的发明专利对其经济高质量发展有促进作用，这体现了创新对于社会发展的重要意义。提高创新能力，加大创新对社会经济的影响应注重以下几个方面。首先，应从公众角度提高社会公众的产权意识。其次，专利数量是衡量地区创新能力的一种方法，应重视创新质量的提升，要协调专利数量和质量的协调发展。最后，提高各产业积极投身于创新研发的动力，激励更多的人们投身于高质量创新的事业中，不断促进社会主义市场经济的发展。