高压直流输电线路的非对称设计

高 森

（国网江苏省电力有限公司扬州供电分公司，江苏 扬州 225000）

高压直流输电线路非对称设计是为了满足系统运行要求，通过考虑线路参数、线路结构和输电设备等方面的非对称性，提高线路的输电能力和可靠性。设计高压直流输电线路时，需要考虑线路的参数非对称性，如线路电阻、电抗和电容等的差异。合理的设计可以降低线路阻抗的非对称性，提高线路的输电能力。还需要考虑输电设备的非对称性，如换流变压器和换流器组等。合理的设计可以降低输电设备的非对称性，提高输电系统的稳定性和可靠性[1-2]。

1 高压直流输电线路设计限制条件

从可接受的对称HVDC 架空线路设计和工作电压开始，最大负电压增加即保持正梯度恒定，可以通过如下方面进行确定。1）基于对异常闪络的考虑，为负导体梯度设置任意限制。2）地面电场感知。3）绝缘和间隙问题。限制条件取决于基本情况下的电压、配置和导体尺寸。由于直流绝缘在很大程度上取决于耐污染强度[3-5]，因此由中等程度的不对称性导致的雷电性能变化对设计影响较小。

根据不同的应用，同轴电缆可设计为不同的阻抗、不同的材料和带宽，其特性阻抗（Z0）通过公式（1）近似得到。

式中：μ和ε分别是介电磁导率和介电常数；R2是外电极半径；R1是中心半径。

在公式（1）中，同轴电缆电极半径的变化决定其特性阻抗。由于大多数局部放电测量实验台是通过平板连接到数据采集系统的，因此，应用同轴热释光法测量局部放电脉冲有一定难度。在该情况下，如果将同轴输电线路（TL）的中心电极视为平地电极，那么局部放电实验台的TL 尺寸将显著大于连接电缆的尺寸，并提供了终端问题解决方法。

本文推荐了一种替代方法，在局部放电测量装置的底部增加一个圆锥形TL，以便为接地电极提供更大的接地面积，并为测量电缆提供更好的终端。此外，在本文设计中，高压代表激励点，R是限流电阻，CC 是耦合电容，TO 是局部放电源。锥形TL 的特性阻抗计算如公式（2）所示。

式中：θ1和θ2分别是TL 的中心和外电极角度。

高压直流输电过程中换流器消耗的无功功率如公式（3）、公式（4）所示。

式中：P为换流器直流侧功率，MW；φ为换流器的功率因数角；μ为换相角；α为整流器触发角。

当换流器以逆变方式运行时，公式（4）中的α用γ代替，γ为逆变侧关断角。

2 高压直流输电线路构建

导体梯度极限增益如图1所示。不对称优势的第一个近似值可以通过图1 的简单、恒定高度双极配置来证明，其中+/-200kV 的平衡直流电压（横坐标上的左、右点）导致出现大约20kV/cm 的导体表面梯度。地面水平电场和AN水平非常低。在该横坐标值处，负电压可以增加。降低正电压以保持恒定的正梯度。在负梯度达到27kV/cm 前，可以增至大约294kV，该情况下需要设置极限值。由于正电压调整，AN保持不变，并在平衡电压下比功率的额定功率增约22%。

图1 导体梯度极限增益

假设原始平衡电压增加，在横坐标上向右移动，则起点AN增加，并且根据上述规则，负电压的百分比增加较小，功率增加也遵循此规则。假设原始平衡电压在两极（横坐标上最右边的点）产生等于本文最大设定值（27kV/cm）的起始点梯度时，负电压不再增加。如果图1 增加极间距和负导体高度以适应更高的负电压，进而可实现更高的总电压，暂时忽略地面场感知可能施加的任何限制，因此，图1 中的增益是保守的。

假设正极在顶部进行垂直配置且正极在底部具有更大优势，则会产生类似的电压优势。使用如图2所示的三导体束并仅将最大导体梯度作为约束来重复图1 的水平情况，则可以维持较高电压，但在该例中，地面电场感知效果会减弱。

图2 受场感知限制的增益

感知水平s是输电线路工作站建议的等级，其中等级1是“刚刚可感知的”，2 是“绝对可感知的”，3 是“超出感知极限”。在该情况下，感知可能会成为不对称性的限制，并取决于起点电压。类似图2 的结果也适用于垂直阵列。将s作为假定的感知指数，或地面电场E、离子电流密度J这2 个影响感知的因素进行计算较复杂，一般通过相关专业软件来实现。虽然模型的结果并不总是一致的，并且取决于配置，但一份研究结果显示，负极的E和J都大于正极，感知s可能比图2 和图4所示的更严重，其中s被描述为极限。

上述基本两极情况可以扩展到分裂双极和三极阵列，这2 种阵列对平均或小导体尺寸都将显示出受表面梯度限制的相似优势模式，并将感知水平作为较大导体尺寸或束限制的前提条件。

3 实例验证

3.1 线路设计参数

基于上述结果，本文对250kV、400kV、500kV 和600kV水平配置的HVDC 线路示例进行了详细建模，每个示例都借鉴目前使用的线路标准尺寸，并运用不对称设计、建造了一条性质相同、性能更优的高压直流输电线路。

表1 线路参数

图3 500kV 配置

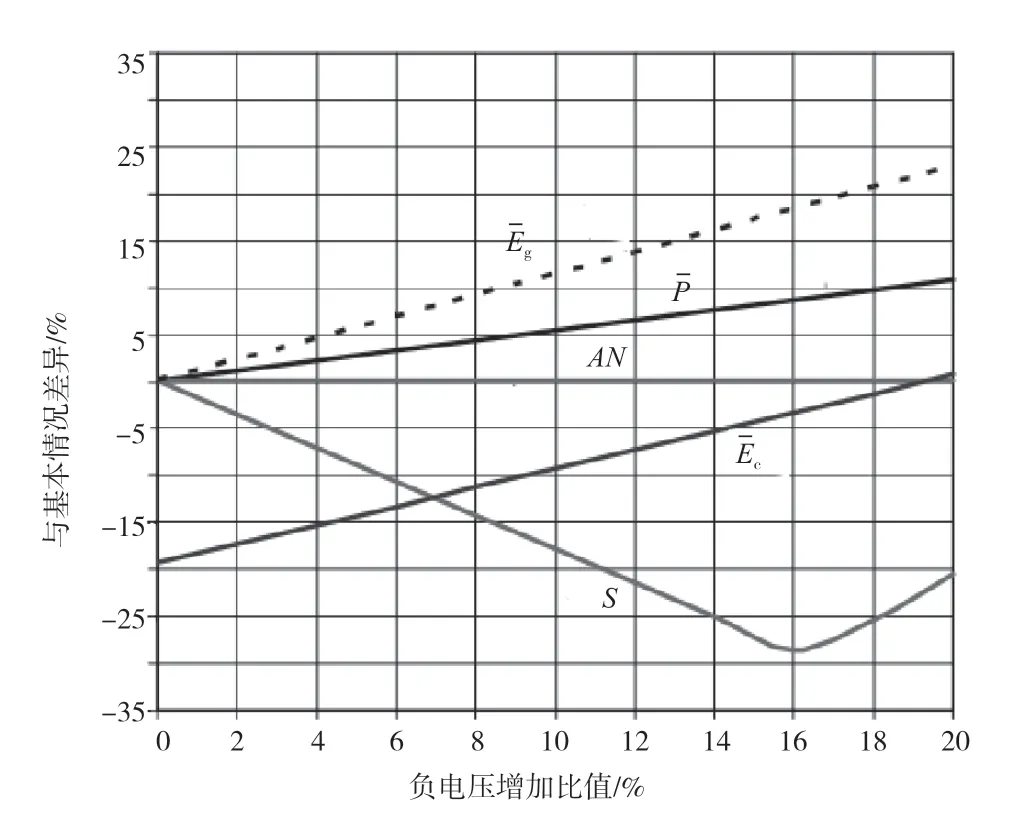
图4 非对称结果500kV 示例

图4 中的500kV 示例假设有18 个6.5 盘式绝缘子，每个具有508mm 的绝缘距离，特定绝缘距离约为23mm/kV，总串长为117。假设电极电压相等，该绝缘串如图5（a）所示，正极长度的10%调整如图5（b）所示。该极性具有更好的污闪性能。图5（c）对负极进行了2 次修正，增加了绝缘体的数量，以适应负电压10%的增加值，并略微提高了悬挂点，上述增益将提高电气部件安全规范间隙要求。图5（d）将这些调整扩展到负电压增加20%的幅度。

图5 500kV 绝缘和高度调整示例

图5（d）中20%的不对称情况要求负极导线的悬挂点增加约“36”，对新结构来说较合理，但对分配给负极负载的交流相位而言会出现新的问题。如果在20%不对称的情况下将负极的横向保持固定，导线悬挂点升高“10”（25.4cm）以满足规范要求，那么绝缘空间的垂直分量会减少约10/117=8.5%，而剩余垂直距离的承受要求会增加20%。此改进顺序可能较难通过“转换为长棒绝缘体”选项来实现，但显然可以通过“转换为浮动端配置”来实现，其中额外的爬升距离主要在水平面内实现。

3.2 仿真结果

在上文的实例中，对所实现的MW 增加来说，绝缘体数量净增加的成本非常小。但是负导线的悬挂点越高，塔架的横向力矩越大，并通过略微降低正悬挂点而部分影响偏移。根据图5所示，对于10%的不对称性，力矩增加约为0.7%，对于20%的不对称性，则增加1.7%。作为一阶近似，塔架成本约随水平力矩的平方根而增加，因此，对于上述2 个不对称水平，塔架成本分别增加了约0.4%和0.8%。

使用示例塔架质量，假设钢构件的成本为26 元/kg，采用2 ∶1 的乘数进行架设时，在不对称性为10%的情况下，增加400kV 输电线路容量的成本约为67.5 元/MW·km，在不对称度为20%的情况下约为150 元/MW·km，两者比新建实现的容量成本低一个数量级以上。

换流站不对称的成本需要与输电线路的成本相加，该成本因不同的电力公司会有所不同。尽管有线性整流器（LCC）转换器，但其适用于电压源（VSC）转换器的第一近似值，每千瓦的成本会随额定值的增加而下降，并接近更高额定值的水平值。考虑对相同的额定电流老说，增加直流电压主要是靠更多的开关和更高的变压器电压，其他变电站成本不受影响，因此，与输电线路本身相同，不对称换流站容量的增量成本可以小于原始站容量的成本。

4 结论

HVDC 线路的不对称设计或电压分配具有较大优势，具体如下：1）载双极电压受导体梯度效应限制的情况下，将负极电压增加约20%，同时略微降低正极电压，可获得10%的MW 额定增益。对已经在低导体表面梯度下操作的线路来说，该增益是最高的。2）在主要关注地场效应的情况下，不对称性的优势更明显，并取决于对正电场与负电场的相对大小和离子电流密度的假设。3）通过不对称性增加输电塔MW额定值的增量成本比新建工程的每MW公里成本低一个数量级。4）本文分析未考虑损失。然而，出于对异常闪络的考虑而制定的导体表面梯度限制，可以将损耗限制在合理水平。5）在每MW 公里输电线路容量增量成本较高的前提条件下，高压直流线路非对称性设计是最具优势的。