条带型加糙体尺寸及加糙量对矩形明渠糙率的影响

邹俊

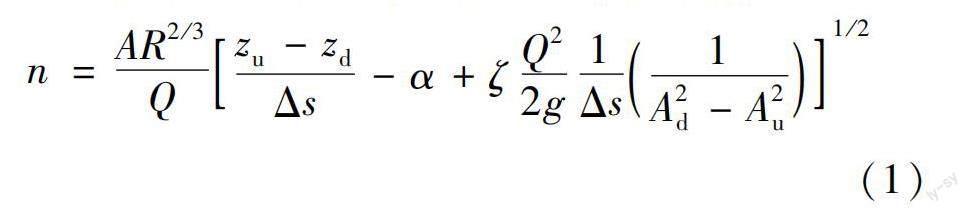
摘要：为研究条带型加糙体的尺寸及加糙量对矩形明渠糙率的影响，利用水工模型试验方法，设计了7种加糙体几何尺寸及3种加糙量工况，定量分析了加糙体参数与糙率之间的关系。结果表明：间距与高度比一定时，加糙体尺寸越大糙率越大，且系列数据表明加糙体尺寸与糙率呈线性规律，其斜率受加糙量影响，该线性规律可被用于反推加糙体的尺寸。加糙量与糙率呈现正相关性，但断面加糙量变化导致的糙率变化并不与加糙量变化呈等比例变化。随着加糙体尺寸的增加，糙率比值呈现增加趋势，加糙体尺寸的变化可放大断面加糙量变化带来的糙率变化。研究成果可为水力学模型以及实际工程的加糙提供参考。

关键词：糙率；条带型加糙；加糙量；水工模型试验

中图法分类号：TV131 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2024.02.014

文章编号：1006-0081（2024）02-0088-06

0 引 言

糙率n是反映水流阻力影响的一个综合性系数。在水工模型试验中，选取合适的糙率n十分关键。当模型或工程材料的糙率无法满足要求的较大糙率值时，需进行加糙。常见加糙手段包括点块型加糙、条带型加糙、膜片型加糙等，见图1。加糙范围包括底板（河床、滩地、水槽底板等）、侧壁（岸坡、水槽边壁等），见图2。粘贴条带加糙属于条带型加糙的一种，是将有机玻璃、塑料等材质的加糙条按照一定的规律粘贴在固体边界上，比同属于条带型加糙的凹槽加糙的糙率相对更大，比同属于条带型加糙的水中拉线加糙的适用范围相对更广。与点块型加糙相比，条带型加糙（主要是粘贴条带加糙，下同）在某些场合更简便，易于实施，如规整的河道或水槽。

作为一种简便、效果较好的加糙手段，条带型加糙具有尺寸与分布易控制的优点，在理论研究与实际工程中均有运用。了解条带加糙方式的作用机理，掌握关键参数对加糙效果的影响，能更好地发挥其在研究和工程中的作用，提高研究、设计人员的工作效率。

Knight等研究了方形条带型加糙体的加糙体间距与阻力的关系。惠遇甲、胡春宏利用侧壁条带型加糙体改变试验水槽糙率以研究边壁糙率对阻力的影响。杜国仁在条带加糙的水槽中研究人工加糙水槽的河床基准面问题。卞华等研究了方形、圆形、半圆形、三角形条带型加糙體的水流结构，认为加糙体间距l/高度Δ=8时水流阻力最大。Hyun等研究了条带型加糙（仅底板）下的水流特征，认为l与Δ比值为1∶7时比1∶3.5时对水流的粗糙影响程度更大。Guo等认为条带型加糙体的间距对流量有明显的影响，随着两条带间距的增大，加糙体之间的涡流增大，当l/Δ≥7时，加糙体之间发生了流动的重附着现象。林金裕通过试验研究了条带型加糙体间距与高度比对糙率的影响。毛冉冉等研究了条带加糙下的流速分布特征。条带加糙型式也应用到了实际工程中，例如溢洪道的泄槽人工加糙。

以往的研究对条带型加糙体的加糙效果进行了探讨，主要是条带型加糙体的间距、形状对水流阻力的影响。本文针对条带型加糙体的几何尺寸及加糙量与矩形明渠糙率的关系开展试验研究与定量分析，试图基于系统试验探索加粗体几何尺寸、加糙量与糙率的规律关系，提出计算相关公式，综合辨别糙率在多因素下的规律。研究成果可一定程度反映条带加糙方式的糙率变化规律，为水力学模型及实际工程加糙提供参考。

1 水工模型试验

1.1 试验水槽

利用循环水槽进行物理模型试验。物理模型由顺直水槽、供水系统、回水系统、量测系统等组成。顺直水槽采用透明有机玻璃制作，长9.6 m，均为矩形断面，断面宽0.49 m，高0.30 m，整体坡度为0，水槽末端设置尾门，见图3与图4。供水管道设置有电磁流量计与阀门。

1.2 条带型加糙体

研究认为矩形条带的加糙效果最好，且加糙条间距与高度比l/Δ=8左右时，加糙效果明显。本试验的条带型加糙体选取硬质PVC方管，加糙体高度Δ为3.0～29.2 mm，l/Δ=9，l为相邻加糙体截面中心线之间的距离，见图5。

1.3 水流参数

糙率系数n不是一个单纯反映边界粗糙状况的系数，还受到水力要素和水流特性的影响。本试验在同一恒定流量下进行，进口流量为0.032 5 m/s，代表性水力学参数见表1。

1.4 试验工况

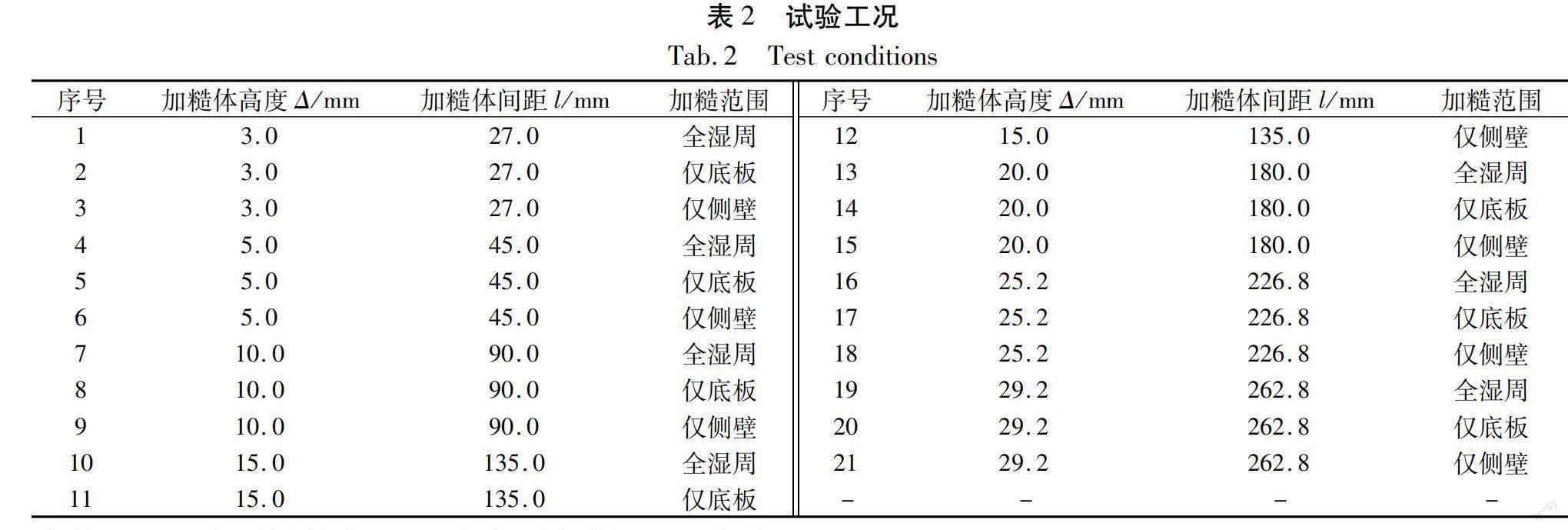
选取3.0，5.0，10.0，15.0，20.0，25.2 mm与29.2 mm共计7种不同几何尺寸（正方形截面的尺寸特征由高度Δ代表）的条带型加糙体，按加糙范围又分为全湿周（范围1）、仅底板（范围2）与仅侧壁（范围3）3种，工况见表2。控制上游流量与下游水位，测量水槽沿程水面线，采用式（1）计算综合糙率。

式中：Q为流量，m/s；A为断面面积，m；R为水力半径，m；Δs为区间长度，m；z为水面高程，m；g为重力加速度，m/s；α为动能修正系数，ζ为局部水头损失系数。下标u表示上游，下标d表示下游。

2 结果分析

2.1 加糙体尺寸对糙率的影响

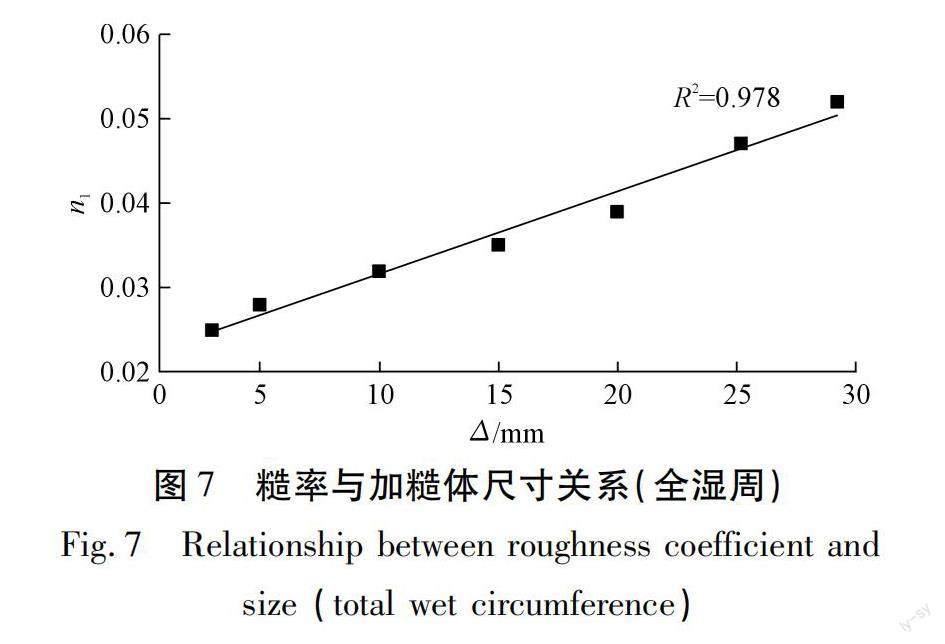
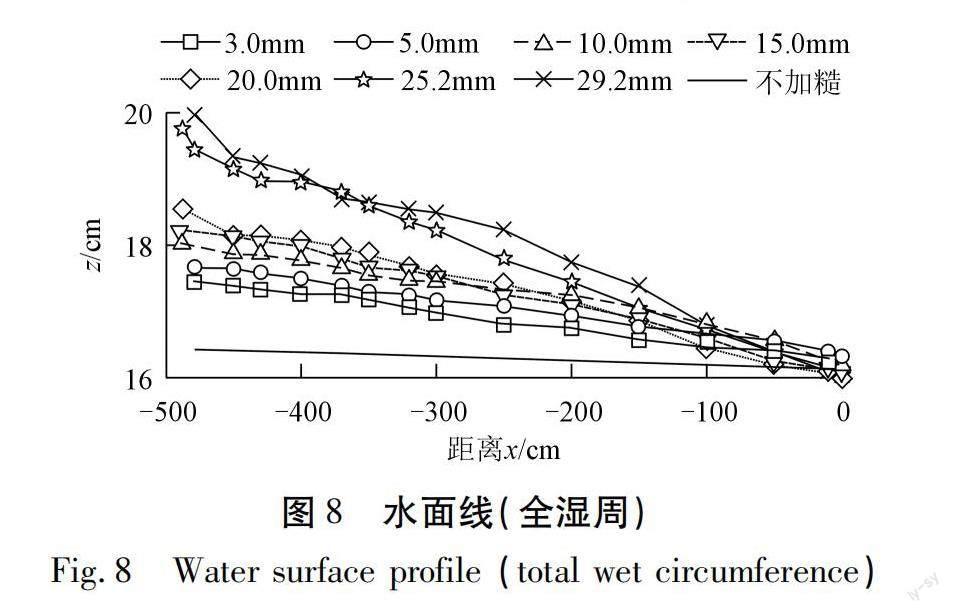
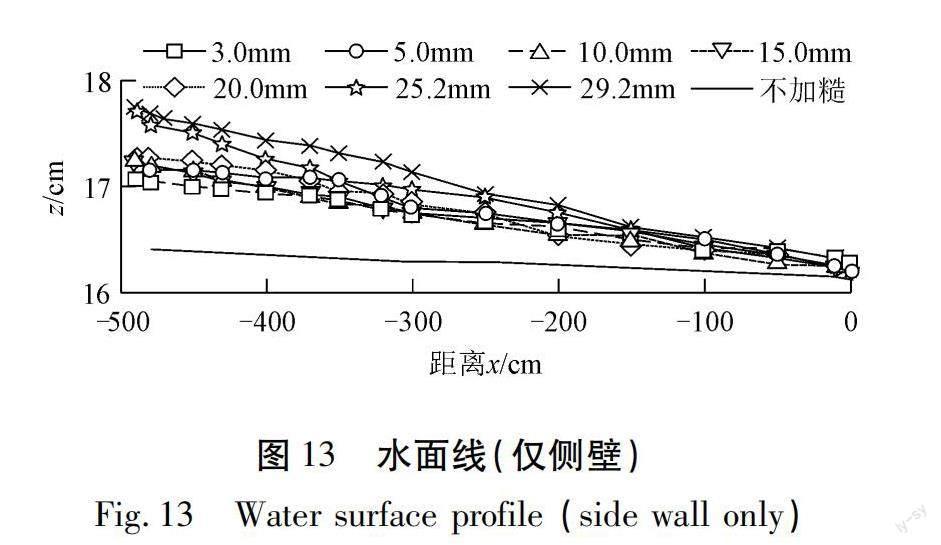
全湿周加糙，即底板与侧壁均加糙，见图6。糙率与加糙体尺寸关系（全湿周）见图7。沿程水面线成果见图8，全湿周加糙系列各工况的水面线基本沿程降低。同一流量前提下，随着加糙体几何尺寸的增加，水面高程整体呈现增加趋势，加糙体尺寸是水面线的决定因素。几何尺寸较大的 25.2 mm与29.2 mm加糙体工况的水位升高明显。加糙体尺寸的增加增大了水流阻力。仅底板加糙系列试验（图9～11）与仅侧壁加糙系列试验（图12～14）的水面线规律与全湿周加糙系列试验相似。

全湿周加糙系列试验在区间x=-479～0 cm，未加糙的工况的水面整体比降J（下标“1”代表全湿周加糙系列试验）为0.000 61；3.0 mm加糙体的整体比降J为0.002 4；29.2 mm加糙体的整体比降J为0.008 2；7个加糙工况的比降J较未加糙工况增大4.0～13.5倍，变化明显，详见表3。仅底板加糙系列试验在区间x=-479～0 cm，比降相对全湿周加糙系列试验有所减小，3.0 mm加糙体的整体比降J（下标“2”代表仅底板系列试验）为0.001 8;29.2 mm加糙体的整体比降J为0.004 7;7个加糙工况的比降J较未加糙工况增大至3.0～7.8倍。仅侧壁加糙系列试验在区间x=-479～0 cm，比降相对全湿周与仅底板加糙系列试验有所减小，3.0 mm加糙体的整体比降J（下標“3”代表仅侧壁系列试验。）为0.001 6；29.2 mm加糙体的整体比降J为0.002 8；7个加糙工况的比降J较未加糙工况增大至2.6～4.7倍。

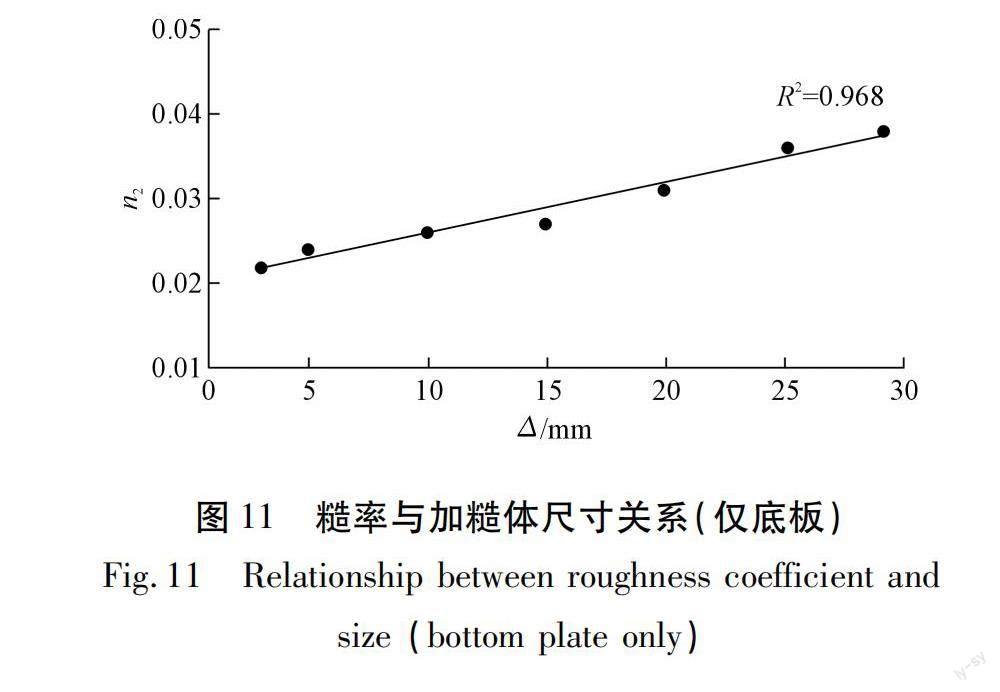
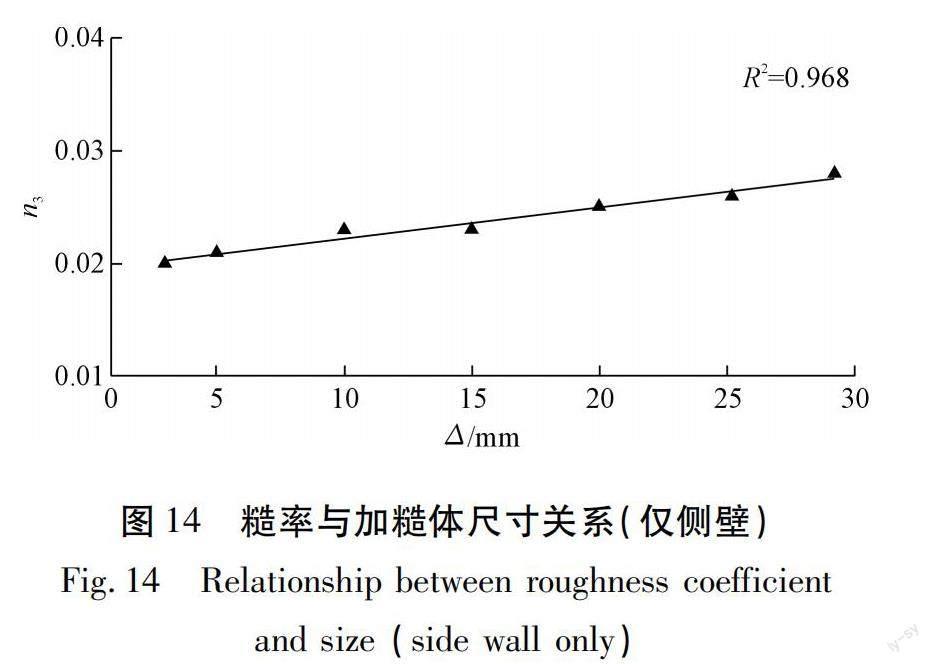
糙率n随着加糙体尺寸的增大而增加，全湿周加糙系列试验的n上升至0.025～0.052，仅底板加糙系列试验的n上升至0.022～0.038，仅侧壁加糙系列试验的n上升至0.020～0.028，见图7，11，14。且糙率n与加糙体尺寸呈现一定的线性规律，见式（2）～（4）。

n=0.00098Δ+0.022    （2）

n=0.00060Δ+0.020    （3）

n=0.00028Δ+0.019    （4）

水流运动时，条带型加糙体后一定范围形成了漩涡区，漩涡导致主流与加糙体后的固体边界一定程度分离，使得加糙体后的固体边界对水流的影响被削弱，尤其是加糙体间距较小时。此时，当加糙的量到一定程度，加糙体本身的几何特性对整体糙率的影响是主导性的，因此，试验中不同的加糙范围不影响糙率与加糙体尺寸的线性规律。对于宽深比较小的水流，加糙量到达一定程度且未加糙区的糙率不大时，存在此类线性规律，可通过少量的条带加糙试验得到线性系数，进而反推得到其他所需糙率的加糙体尺寸。

2.2 加糙量对糙率的影响

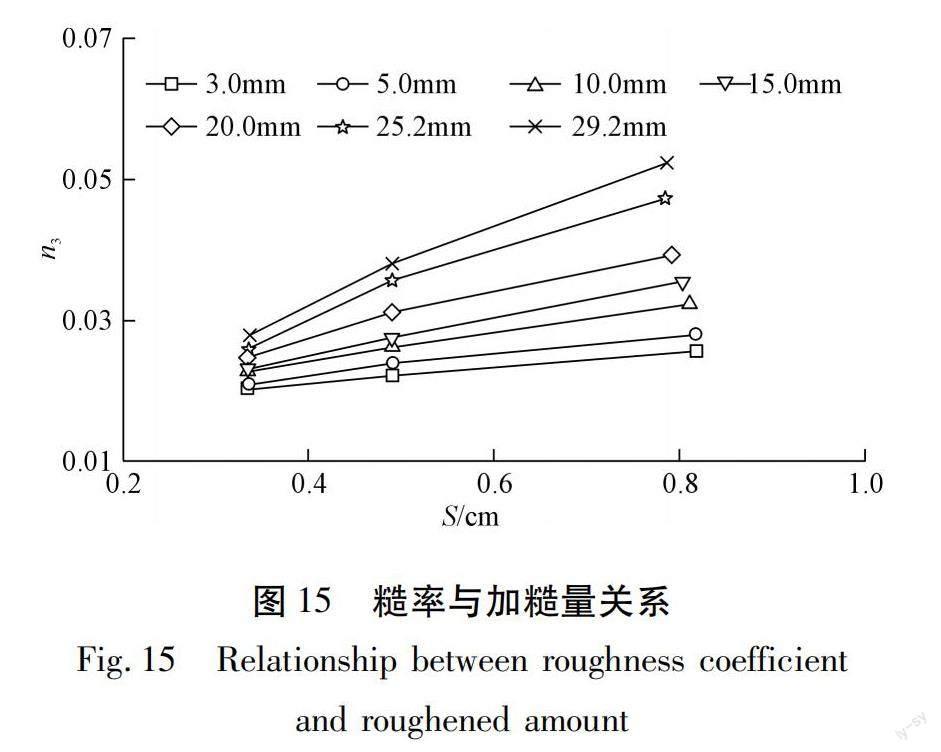
加糙体尺寸与间距相同的情况下，全湿周加糙、仅底板加糙与仅侧壁加糙的区别在于加糙范围（加糙量），即加糙断面上加糙体的体积、面积或长度不同。按加糙断面上的加糙长度S考虑，本次试验全湿周加糙为断面完全加糙，加糙量最大，也是加糙量的极限情况，其余为部分加糙，仅底板加糙的加糙量次之，仅侧壁加糙的加糙量最小。加糙量越大，水流阻力越大，水面线高程相对更高，加糙量与糙率呈正相关，见图15。对比式（2）～（4），三者的区别主要在线性关系的斜率部分，分别为0.000 98，0.000 60，0.000 28，截距的区别较小，分别为0.022，0.020，0.019，可见斜率的差异与加糙量密切相关。

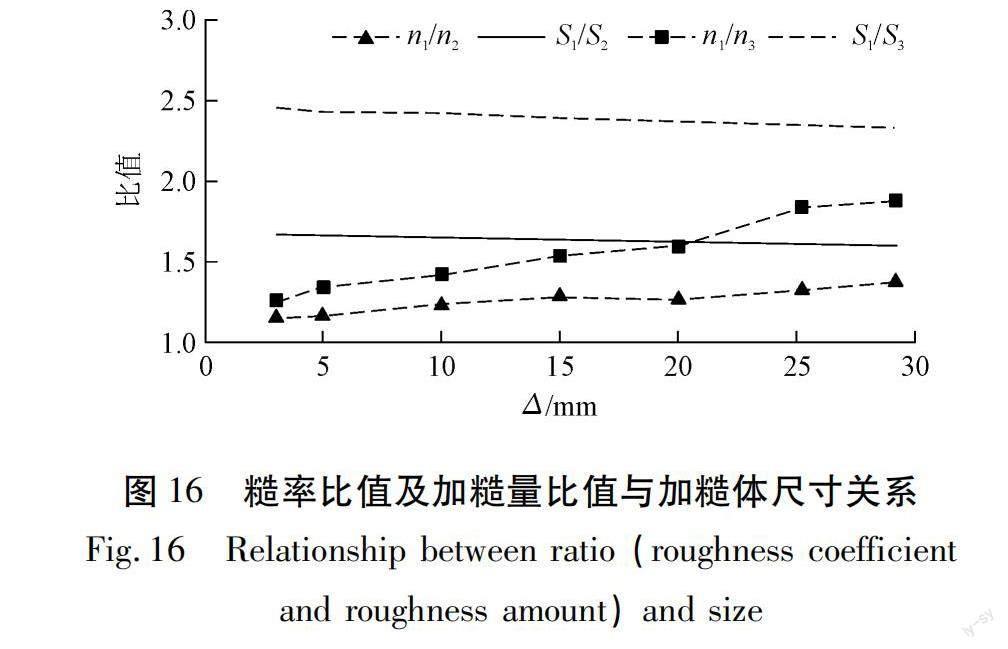
基于试验数据进一步分析，与全湿周加糙系列试验相比，无论是仅底板加糙系列试验还是仅侧壁加糙系列试验，在断面有效加糙长度比值，即加糙量比值S/S（i=2，3，下同）基本稳定的情况下（S/S=1.60～1.67，S/S=2.33～2.45），随着加糙体尺寸的增加，糙率比值n/n随之增加（n/n=1.16～1.38，n/n=1.26～1.88），且大于1.0，但小于相应的加糙量比值S/S。因加糙量增大导致的糙率增大并不与加糙量变化等比例，且随着加糙体尺寸的增加，糙率比值呈现增加趋势，但糙率变化明显小于加糙量的变化。因此，对于条带加糙，当加糙体尺寸较小时，增大断面加糙量对糙率的提升效果相对有限，而加糙体尺寸的变化可放大断面加糙量变化带来的糙率变化，见图16。

3 结 论

针对条带型加糙体几何尺寸及加糙量对矩形明渠糙率的影响开展试验研究与定量分析，主要结论如下。

（1）加糙体间距与加糙体高度的比值一定的情况下，加糙体几何尺寸越大，糙率越大，且试验中的条带型加糙体尺寸与糙率呈现一定的线性规律，不同的加糙范围不影响该线性规律的存在。条带型加糙体后的漩涡区削弱了加糙体后的固体边界对水流的影响，当加糙的量到达一定程度时，加糙体本身的几何特性对整体糙率的影响是主导性的。试验结果一定程度揭示了条带加糙方式的糙率变化规律。在加糙设计时，可利用该线性规律，反推得到所需条带型加糙体的尺寸。

（2）在條带型加糙体的几何尺寸与加糙间距相同的情况下，加糙量与糙率呈正相关，加糙量越大，糙率越大，加糙量显著影响了加糙体尺寸与糙率的线性关系中的斜率系数。本次研究初步建立了加糙量与该线性关系之间的联系。

（3）断面加糙量变化导致的糙率变化并不与加糙量变化等比例。随着加糙体尺寸的增加，糙率比值呈现增加趋势，但糙率变化明显小于加糙量的变化。对于条带加糙，加糙体尺寸较小时，增大断面加糙量对糙率的提升效果相对有限，加糙体尺寸的变化可放大断面加糙量变化带来的糙率变化。

参考文献：

［1］ 吴持恭.水力学［M］.北京：高等教育出版社，2008.

［2］ 李甲振，郭永鑫，甘明生，等.河工模型试验加糙方法综述［J］.南水北调与水利科技，2017，15（4）：129-135.

［3］ 谢鉴衡.河流模拟［M］.北京：水利电力出版社，1990.

［4］ 牟小玉.河工模型碎石加糙阻力试验研究［D］.重庆：重庆交通大学，2019.

［5］ 孙东坡，李全家.水力模型制作的一种新型加糙方法［J］.人民长江，2014，45（3）：87-89.

［6］ KNIGHT D W，MACDONALD A J.Hydraulic resistance of artificial strip roughness［J］.Journal of the Hydraulics Division，1979，105（6）：675-690.

［7］ 惠遇甲，胡春宏.矩形明槽宽深比和边壁糙率对于流速分布和阻力影响的实验研究［J］.水科学进展，1991（1）：22-31.

［8］ 胡春宏，惠遇甲.矩形明渠宽深比和边壁糙率对流速分布的影响［J］.人民黄河，1987（2）：19-24.

［9］ 杜国仁.具有人工加糙底部的河槽的水力学计算［J］.人民长江，1995（8）：55-56.

［10］ 卞华，李福田，蒋慧敏，等.二维加糙明渠的阻力特性［J］.河海大学学报，1997（6）：114-117.

［11］ HYUN E J，SUH T Y.Turbulent flow over two-dimensional rectangular-shaped roughness elements with various spacings［C］∥IEEE.OCEANS 2006-Asia Pacific.Singapore：IEEE，2006.

［12］ GUO Y K，ZHANG L X，SHEN Y M，et al.Modeling study of free overfall in a rectangular channel with strip roughness［J］.Journal of Hydraulic Engineering，2008，134（5）：664-667.

［13］ 林金裕.矩形糙条间距对床面糙率影响的实验研究［J］.水道港口，2020，41（5）：539-544.

［14］ 毛冉冉，程年生，卢叶盛.二维加糙明渠流理论床面的确定方法［J］.泥沙研究，2022，47（6）：9-14.

［15］ 苟兴智.溢洪道明渠弯道冲击波控制简述［J］.陕西水力发电，1986（3）：44-56.

［16］ 康德民，黄显旗，詹承偶.槽底采用双人字形齿槛加糙［J］.小水电，1997（1）：27-28.

［17］ 张明义，戚印鑫，高建新.乌拉泊水库溢洪道消能防冲模型试验研究［J］.人民黄河，2010，32（3）：83-85.

［18］ 张明义，高建新.人工加糙技术在乌拉泊水库溢洪道陡坡段中的应用［J］.水利规划与设计，2010（2）：57-60.

［15］ 李锦艳.多弯段溢洪道糙条对水流消能导流作用研究［D］.乌鲁木齐：新疆农业大学，2016.

［16］ 魏祖涛，侍克斌，陈成林，等.溢洪道加糙对水流流态影响的试验研究［J］.水资源与水工程学报，2010，21（5）：76-78.

［17］ 贾萍阳.溢洪道弯段泄槽中糙条对冲击波影响分析及布置参数研究［D］.乌鲁木齐：新疆农业大学，2020.

［18］ 杨岑，路泽生，栾维功，等.矩形渠道人工加糙壁面阻力规律试验研究［J］.长江科学院院报，2011，28（1）：34-38.

［19］ 赵锦程.人工渠道糙率影响因素的试验研究［D］.乌鲁木齐：新疆农业大学，2013.

［20］ 赵锦程.不同断面形状对人工渠道糙率影响的试验研究［J］.西北水电，2015（2）：79-81.

（编辑：江 文）

Influence of geometric size and roughened amount of strip roughened

element on roughness of rectangular open channelsZOU Jun

（Jiangxi Academy of Water Science and Engineering，Nanchang 330029，China）

Abstract：To study the effects of geometric size and roughened amount of strip roughened element on the roughness of rectangular open channels，a physical model test method was used，involving seven types of geometric size and three types of roughened amount. The relationship between the roughness and the parameters of the roughness elements was quantitatively analyzed. The results indicated that when the ratio of the spacing to the height of the roughened element was constant，the larger the size of the roughened elements，the greater the roughness. The series of data showed that the size of the strip roughened element exhibited a certain linear relationship with roughness，and the slope of this linear relationship was influenced by the roughened amount. This linear rule can be used to infer the size of the roughened element required for roughening. There was a positive correlation between roughened amount and roughness，but the change in roughness caused by the change in roughened amount was not proportional to the change in roughened amount. As the geometric size of the roughened element increased，the ratio of roughness showed an increasing trend. The change in the geometric size of the roughened element can amplify the change of roughness caused by the change in roughened amount. The research results can provide a references for roughening work of hydraulic models and actual projects．

Key words：roughness；strip roughening；roughened amount；hydraulic model test