混合泊位分配与专用泊位租赁的联合优化研究
2024-03-03郑建风王鑫珏刘惠斌
郑建风,王鑫珏,刘惠斌
(大连海事大学,交通运输工程学院,辽宁大连 116026)
0 引言
为应对需求增加对港口管理的挑战,许多港航企业通过建设专用泊位等方式进行合作,以提高港口的运营水平,泊位分配问题(Berth Allocation Problem,BAP)是港口运营时资源调度中的关键问题。本文在港航合作的背景下,考虑泊位类型的区别以及船舶和船公司的隶属关系,以班轮公司为主体,研究一个新颖的混合泊位分配问题以及专用泊位租赁决策问题,对港口泊位资源分配的集成优化研究具有重要意义。
宋云婷等[1]通过对货场分配与泊位调度的研究,证明集装箱码头泊位调度的复杂性,为到港船舶制定靠泊计划是港口管理的重要问题。BAP 也可与其他资源分配或调度问题一并考虑。部分学者将BAP 与港口其他资源的分配及调度问题进行联合优化(或集成优化)。例如,Park和Kim[2]将岸桥分配与BAP 进行联合优化;Wang等[3]将堆场资源分配优化引入到BAP 中;Liu等[4]将船舶在航道通行的优化引入到BAP中。不确定性也是BAP研究中的重要问题,Zhen等[5]在泊位与堆场联合优化中考虑船舶的不确定性;Ji等[6]与Chargui等[7]分别为不确定到港时间的BAP 设计了NSGA-II 与精确的分解算法。绿色港口与合作背景是近期BAP 研究中较为热点的问题。考虑环境效益,Yu等[8]和Zhen等[9]在泊位和岸桥的联合优化中引入绿色港口的概念与相关应对措施。在合作的视角下,Msrtin-Iradi等[10]和杨劼等[11]以合作博弈的视角分别采用数学分析和优化的方式研究了港口群内多港口通过共享港口资源的方式进行合作的泊位分配问题。专用泊位的使用正是港航合作的一种形式,如中远海运集团公司在新加坡港签约设立了专用泊位,针对此现象,Guo等[12]研究考虑码头所有泊位均为专用泊位的BAP。基于排队论,Zheng等[13]从战术层面研究多家班轮公司合作租赁专用泊位时的最优专用泊位数与班轮公司之间的最优合作策略。以上研究并未对到港船舶和班轮公司的隶属关系进行区分,且未考虑到有限的泊位数量导致部分班轮公司船舶需要停靠在普通泊位进行作业的情况,也未在运营层面对专用泊位的租赁决策进行优化。
综上,本文研究一个新颖的BAP,称为混合泊位分配问题(Mixed Berth Allocation Problem,MBAP)。MBAP 即考虑码头同时存在普通泊位与专用泊位的BAP。此外,如何权衡普通泊位和专用泊位的数量以及如何为不同班轮公司确定合适的专用泊位租赁策略是本文研究的一个重要问题。为了解决上述问题,本文研究MBAP和专用泊位租赁的集成问题(MBAP Integrated with Leasing of Dedicated Berths,MBAP-L)。在传统BAP 模型的基础上,引入专用泊位相关的约束,建立MBAP-L的混合整数规划模型,并基于Dantzig-Wolfe分解思想将该模型转化为用两组决策变量分别表示船舶靠泊计划与泊位租赁策略的集划分模型,且以该集划分模型为基础构建可解决本文问题的限制主问题模型与定价子问题模型。基于主问题与子问题模型,设计考虑枚举的列生成(Column Generation,CG)算法,对模型进行求解。最后,通过算例分析与传统的求解方式进行对比证明本文所建模型和算法的有效性及优势,并且通过敏感性分析为港口和班轮公司的运营提出合理建议。
1 问题描述与建模
1.1 符号说明
(1)集合
L——班轮公司集合,L={1,2,…,|L|},|L|为班轮公司总数;
B——码头泊位集合,B={1,2,…,|B|},|B|为码头泊位总数;
V——到港船舶集合,V={1,2,…,|V|},|V|为到港船舶总数;
Vl——班轮公司l的船舶集合,Vl={1,2,…,|Vl|},|Vl|为班轮公司l的到港船舶总数。
(2)参数
——班轮公司l最多可租赁专用泊位的数量(个);
——船舶i在港单位时间运营成本(万元);
——船舶i在进行装卸作业时单位时间装卸成本(万元);
——租赁一个专用泊位的周成本(万元);
ai——船舶i的到港时间;
hir——船舶i在泊位r的装卸时间(h);
E——规划期时间(d);
M——足够大的正数。
(3)决策变量
bir——船舶i在泊位r的开始靠泊时间;
yir——0-1 变量,若船舶i在泊位r靠泊,则yir=1,否则为0;
zijr——0-1变量,若船舶i,j在泊位r靠泊,且i早于j靠泊,则zijr=1,否则为0;
klr——0-1变量,若班轮公司l租赁泊位r作为专用泊位,则klr=1,否则为0;
nl——班轮公司l租赁专用泊位的数量。
1.2 问题描述
通常,普通泊位可以为不同班轮公司的任意船舶提供服务,而为了保证服务质量,班轮公司租赁的专用泊位只为该班轮公司的船舶提供服务。如图1所示,专用泊位的设置会对其他本应使用该泊位的班轮公司船舶产生影响,其中船舶2原计划停靠在专用泊位2,但由于其被班轮公司2 租赁只能改变计划停靠在普通泊位,进而影响了船舶5的靠泊。
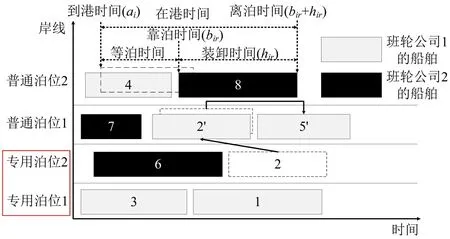
图1 混合泊位分配与专用泊位租赁决策集成问题的示意图Fig.1 Illustration of MBAP-L
为解决上述问题,本文研究的MBAP-L旨在区分船舶所属不同公司情况下,为船舶决策靠泊计划的同时为班轮公司决策泊位租赁计划。其中,泊位租赁计划决策不同班轮公司应该租赁哪些泊位作为自己的专用泊位;船舶靠泊计划决策所有船舶的靠泊泊位和靠泊时间,这两部分均为本文的决策变量。该问题与传统BAP的主要区别体现在:
(1) 需要决策出每一个泊位的性质,如图1中4个泊位起初均为普通泊位,但经过决策后有两个泊位被租赁;
(2)考虑专用泊位时,到港船舶不能随意挂靠,只能停靠在普通泊位或所属班轮公司租赁的专用泊位,因此需要对到港船舶和班轮公司的隶属关系进行区分;
(3)班轮公司租赁专用泊位后会为其配备相应的装卸设备,以此来降低挂靠专用泊位船舶的装卸成本。
由于港口与班轮公司在协商制定靠泊策略时要考虑船舶靠泊、货物装卸和泊位租赁等费用,同时也要考虑船舶平均在港时间过长对港口未来的声誉和收入造成影响。因此本文研究的MBAP-L以总成本最小为目标,总成本包括3 个部分:与船舶在港时间相关的运营成本、与货物装卸时间相关的装卸成本和专用泊位租赁成本,分别用C1,C2,C3表示这3部分成本,即
1.3 模型构建
为便于模型建立,本文考虑如下假设:
(1)本文研究离散型动态BAP,所有船舶的到港时间和装卸时间已知;
(2)所有泊位的物理因素可以满足所有到港船舶,即每一个泊位都可以服务任意到港船舶;
(3)所有船舶的装卸作业在船舶靠泊之后立即执行,忽略部分设备适配过程的时间;
(4)泊位偏好体现在普通泊位与专用泊位之间。
因此,MBAP-L(模型P)可以表示为
式(4)为目标函数,最小化所有班轮公司在规划期内的总成本。式(5)~式(20)为约束条件:式(5)保证每艘船都停靠在某一个泊位,式(6)~式(10)为与专用泊位相关的限制条件,其他约束为传统BAP模型中考虑的限制条件。其中,式(6)和式(7)刻画在班轮公司租赁专用泊位后对船舶靠泊泊位选择的影响;式(8)~式(10)刻画班轮公司租赁专用泊位的方式以及受到的限制。式(6)为模型考虑专用泊位后与传统BAP 模型的主要区别,它保证班轮公司不能将船停靠在其他班轮公司的专用泊位;式(7)保证班轮公司如果租赁了专用泊位,则一定会在这个泊位上进行靠泊,避免专用泊位资源的浪费;式(8)保证一个泊位最多只能被一个班轮公司租赁;式(9)用于计算班轮公司租赁专用泊位的数量;式(10)保证班轮公司租赁专用泊位的数量不能超过上限。式(11)为yir与bir之间的关系。式(12)保证船舶靠泊时间不早于到港时间。式(13)保证同一个泊位连续服务的两艘船舶,后者的靠泊时间不早于前者的装卸完成时间。式(14)和式(15)表达yir与zijr之间的关系,保证停靠在同一个泊位上的两艘船不在时间上发生冲突。式(16)~式(20)给出决策变量的取值范围。模型P 的决策变量不仅仅是不同班轮公司针对两类泊位的决策行为klr,还有所有到港船舶对靠泊时间bir和位置yir的决策(即传统BAP的决策),相较传统BAP模型更为复杂,在问题规模较大时需采用合适的算法求解。
2 算法设计
2.1 模型线性化
为了通过求解器对小规模算例进行求解证明模型的有效性,本文先将模型P进行线性化。由于模型P的目标函数中第3项包含非线性部分klryir,引入0-1 辅助变量ulir=klryir,若班轮公司l租赁了泊位r,并且其船舶i在该泊位靠泊,则ulir=1;否则,ulir=0 。此外,当船舶i未在泊位r靠泊时,yir=0,船舶i在泊位r的靠泊时间bir也为0。此时,目标函数转化为
同时,还需要引入约束
模型LP,可以直接使用求解器求解,但对于大规模问题,很难有效求解。为此,本文将模型进一步转化为集划分模型,并基于此模型设计CG 算法。在CG 算法中,主要思想是将原问题的求解转化为迭代求解限制主问题(Restricted Master Problem,RMP)和定价子问题(Pricing Sub-problem,PSP)。
2.2 集划分模型与限制主问题
CG算法一般适用于求解变量个数较多但约束条件较少的问题。因此,需要将原问题表示为集划分模型。不同于传统的BAP模型,本文的MBAP-L模型除了为每艘船决策出靠泊方案外,还需要为每一家班轮公司决策出专用泊位租赁方案,因此本文提出一个有两组决策变量的集划分模型。这两组决策分别代表船舶的靠泊方案和班轮公司的泊位租赁方案,且将两者之间的关系考虑在约束当中。集划分模型中新增的集合、参数与决策变量如下。
(1)集合
Di——船舶i的可行靠泊方案集合,初始为每一个i对应一个方案d,随着算法迭代增多;
Fl——班轮公司l的可行泊位租赁方案集合,Fl={1,2,…,|Fl|},|Fl|为公司l的泊位租赁策略数量;
T——规划期时间集合,T={1,2,…,|T|},|T|为规划期总时间(168 h)。
(2)参数
ωdrt——0-1 参数,若靠泊方案d中船舶在t时刻占用泊位r,则ωdrt=1,否则为0;
md——0-1 参数,若靠泊方案d中船舶靠泊在专用泊位,则md=1,否则为0;
μfr——0-1 参数,若租赁方案f中泊位r被租赁为专用泊位,则μfr=1,否则为0;
Cd——靠泊方案d的成本;
Cf——租赁方案f的成本。
(3) 决策变量
χd——0-1 变量,当船舶i的靠泊方案d被选择时,则χd=1;
λf——0-1 变量,当班轮公司l的租赁方案f被选择时,则λf=1。
对于每一个靠泊方案d,其成本Cd为
对于每一个泊位租赁方案f,其成本Cf为
式(25)中Cd等于原模型中C1与C2之和,式(26)中Cf等于原模型中C3。
集划分模型可以表示为
式(27)为目标函数,表示所选船舶靠泊方案和班轮公司泊位租赁方案的总成本最小。式(28)~式(35)为约束条件:式(28)~式(31)为传统BAP 的集划分模型中相关约束,其他约束为本文模型新增与专用泊位相关约束。式(28)和式(29)为方案的选择约束,其中,式(29)对应原模型中对班轮公司选择专用泊位的式(8)~式(10);式(30)确保每个泊位最多被一个班轮公司租赁;式(31)确保任何时间,泊位都不能被多艘船同时占用。式(32)和式(33)对应原模型中刻画专用泊位对船舶靠泊策略选择影响的式(6)和式(7),其中,式(32)确保被一个班轮公司租赁的泊位不能停靠其他班轮公司的船舶;式(33)确保只有当某班轮公司将一个泊位租赁为专用泊位时,它的船舶才能以专用泊位的形式在该泊位靠泊。式(34)和式(35)表示两组决策变量取值约束。在模型MP中,做出租赁泊位决策的主体是班轮公司,做出靠泊计划选择的主体是到港船舶,它们并不是独立选择决策的,会受到式(32)和式(33)的相互制约。
由于MP 模型船舶靠泊集合和班轮公司的泊位租赁计划可行方案数量庞大,不易事先给出所有靠泊方案和泊位租赁方案。故初始RMP只考虑部分靠泊方案和泊位租赁方案,并通过求解子问题更新。在CG 算法中,通过松弛RMP 中的式(34)和式(35)以达到获取约束对应对偶变量的目的。
2.3 定价子问题
本文考虑船舶的泊位偏好体现在不同类型泊位之间,可行的泊位租赁方案数量有限,可采用枚举法获得。本节主要求解可行的靠泊方案d。由于问题中同时存在专用泊位和普通泊位,需要考虑任意船舶i以专用(或普通)泊位的形式停靠在泊位r,这两种靠泊方式通过md的取值分别为1 或0 来表示。
为了表示PSP,新添加参数如下:
δi——RMP中式(28)的对偶变量;
ρrt——RMP中式(31)的对偶变量;
σlrt——RMP中式(32)的对偶变量;
τlrt——RMP中式(33)的对偶变量。
在PSP 中,靠泊方案d的降低成本(Reduced Cost)可以表示为
在PSP 中,决策变量除了bir还包括RMP 中的参数ωdrt。对于船舶i停靠在泊位r的方案d,其PSP对应的数学模型为
式(38)确保船舶在到港之后才能靠泊;式(39)表示变量ωdrt中取1的个数等于装卸时间;式(40)和式(41)表达ωdrt与bir之间的关系;式(42)表示决策变量的取值范围。
2.4 算法流程
本文CG 算法流程如图2 所示,首先采用Nishimura等[14]开发的启发式方法获得问题的初始解;其次将初始解转化为可行的靠泊计划,列举出所有可能的泊位租赁计划,并将备选计划导入至RMP 中求解;然后采用枚举的方法求解PSP,并将更优计划加入到RMP中;最后,直到没有列添加至RMP,还原松弛约束并求解,作为问题最终结果。
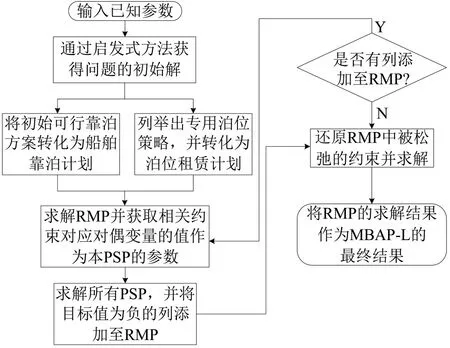
图2 CG算法流程图Fig.2 Flow chart of CG
本文设计的CG算法相较于传统CG算法有如下区别:
(1) 在CG 算法中,RMP 与PSP 均可通过求解器直接求解。但对于本文PSP来说,其决策变量较少,且在一个靠泊方案d中ωdrt与bir有较强的关系(即确定bir就可以确定ωdrt)。因此本文采用枚举法,即可以经过|T-ai-hir|次计算,获得一个PSP的最优解,以此避免反复构建PSP 模型,提升算法的速度。
(2)本文在求解1 组PSP 的过程中将多个更优靠泊方案加入到RMP中,从而加快算法收敛速度,可以应对现实中大规模问题。
3 算例分析
3.1 数据说明与参数设置
本文以在4 家船公司(MSK,COSCO,HMM 和ONE)官网收集的2020 年10 月中1 周内抵达香港港、盐田港和蛇口港的船舶信息为基础进行算例分析。为考虑不同规模的算例,当实际到港船舶数量不满足本文算例规模时,根据郑建风等[15]得出的泊松分布随机产生足够数量的船舶到港时间,并根据以平均装卸时间为期望的均匀分布随机生成对应装卸时间,部分船舶信息如表1 所示。表1 中,第1列代表船舶到港时间服从的泊松分布的参数,第2列代表收集数据中船舶平均装卸时间,后3 列为1周内实际到港船舶数量。
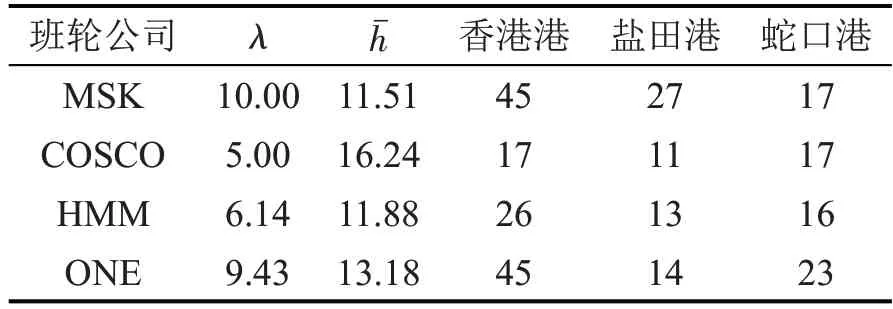
表1 4家班轮公司到港船舶信息Table 1 Information of arriving vessels of four liner carriers
参考相关BAP 研究文献[13,16]的参数设置,本文设置参数如下:单位时间运营成本2095.14 元·h-1,∀i∈V;单位时间装卸成本1047.57 元·h-1,∀i∈V;单泊位每周租赁成本crent=89000 元·周-1,E=7 d;班轮公司租赁专用泊位数量的上限[|B||L|],其中,|B|为泊位数,|L|为班轮公司数。在操作系统为Windows11,主频为3.6 GHz,运行内存为16 G的电脑上,采用python编译算法程序,调用Gurobi 9.5.2求解本文模型,设置最大求解时间为1 h,对算法的有效性进行测试。
3.2 算法有效性分析
为验证本文提出算法的有效性,本节侧重比较3 种求解方法:Gurobi 直接求解原模型LP,RMP与PSP均采用Gurobi求解的CG算法,以及RMP采用Gurobi求解,PSP采用枚举法求解的CG算法。这3种方法分别记为M1,M2 和M3。从结果目标函数值与算法计算时间两个方面比较3 种算法的结果如表2和表3所示。
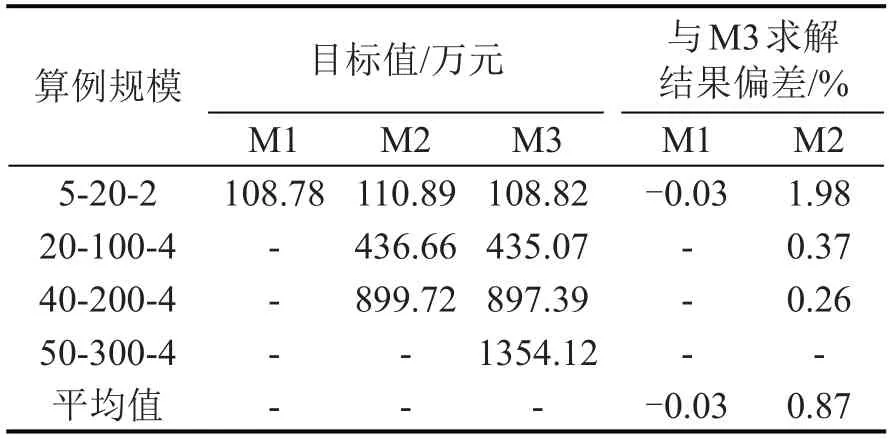
表2 对比不同算例下3种方法得到的目标函数值Table 2 Comparison of objective values in different cases
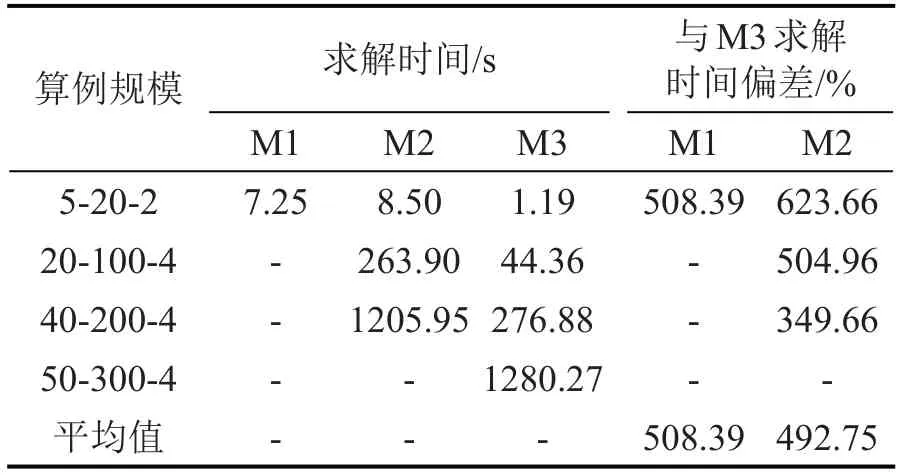
表3 对比不同算例下3种方法的求解时间Table 3 Comparison of computing time in different cases
在表2和表3中,设计4组不同规模的算例,每种规模的算例进行5组测试,并取结果的平均值展示。表中第1列代表算例的规模,例如,算例“5-20-2”表示规模为5个泊位、20艘船、2个班轮公司的算例。通过表2可以发现,在小规模算例中,M3基本能获得与M1 一致的目标函数值,只有部分算例有小于1%的偏差,因此本文提出的M3是有效的。通过表3可以发现,从求解时间来看,M3的求解速度远快于M1与M2。图3表示算例50-300-4-1的迭代情况,纵轴分别表示算法的迭代时间、迭代新增列数以及当代的目标值,由表3及图3可知:

图3 计算收敛过程示意图Fig.3 Algorithm convergence process
(1)算法迭代时间逐代减少,这是因为求解器在构建模型上花费的时间远大于更改已构建模型,这说明本文采用枚举法求解PSP,能够通过避免反复构建模型加快求解速度,证明了算法的有效性。
(2)新增列数与目标值均在前两代显著减少,而后变化很小,这是因为初始解是由启发式方法求解获得,距离最优解差距较大,而本文算法能够在一次迭代中加入多个对目标值有改善效果的靠泊计划,促进算法的快速收敛。
3.3 租赁策略对泊位计划影响分析
为研究不同租赁策略对港口泊位计划以及班轮公司各项成本的影响,并证明MBAP-L模型的有效性,本文选取“40-200-4”规模的算例进行分析。不同专用泊位租赁情况下,船舶的在港时间以及班轮公司的成本情况如表4 所示。其中,第2 列代表4家班轮公司租赁专用泊位的数量,第3列和第4列为船舶在港时间。现实中,专用泊位会配置装卸效率更高或数量更多的设备,从而提高装卸效率。表4中第3列和第4列括号内的数据为船舶挂靠专用泊位减少5%装卸时间时的船舶在港时间。在案例1中,4家班轮公司均没有租赁专用泊位,相当于传统BAP 模型结果。为更直观地表现MBAP-L 与传统BAP 的结果差别,选取案例1 及案例5 中4 家班轮公司具体计算结果展现在表5中。

表4 不同租赁策略下泊位计划效果对比Table 4 Comparison of berth planning in different berth leasing strategy
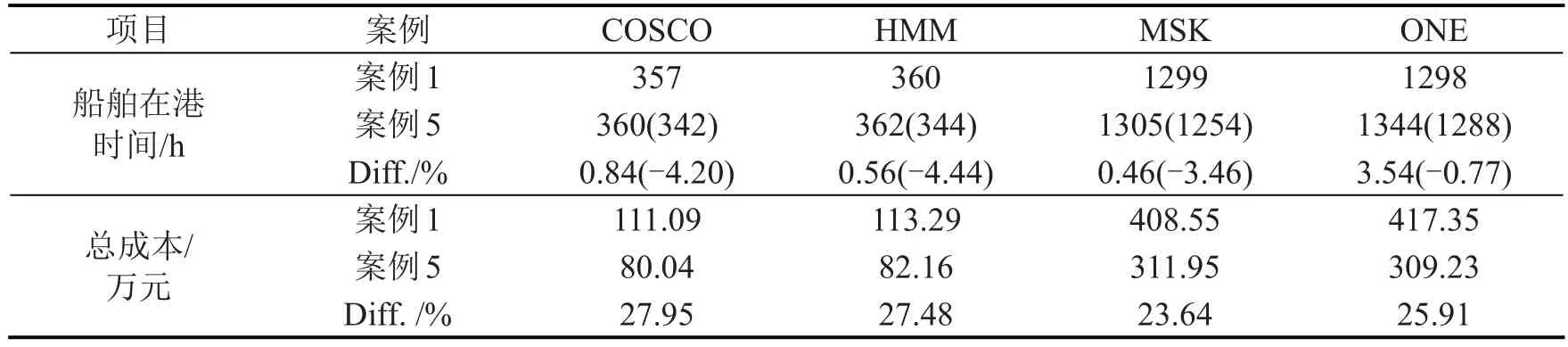
表5 案例1与案例5中各班轮公司结果对比Table 5 Comparison of four liner carriers in case 1 and case 5
由表4 和表5 可知,相较于传统BAP 结果的案例1,4 家班轮公司在案例5 中的总成本分别降低27.95%、27.48%、23.64%和25.91%,可见本文提出的MBAP-L可以大幅度降低班轮公司的运营成本,进而为班轮公司节省总成本,且随着租赁专用泊位的增加,成本下降显著。从船舶在港时间来看,当挂靠专用泊位不影响船舶装卸时间时,大量使用专用泊位会使船舶在港时间平均增加1.35%。这是因为本文考虑的专用泊位,只能服务其所属船公司的船舶,使得泊位利用率降低,从而增加船舶在港等待时间。根据现实情况,考虑船舶在专用泊位作业可加快5%装卸速度时,4家班轮公司的船舶在港时间分别降低4.20%、4.44%、3.46%和0.77%,总船舶在港时间降低2.66%。因此,专用泊位的使用在现实应用中可以实现降低船舶在港时间与降低成本等多方面获利,达到港航共赢的目的。
3.4 敏感性分析
本文敏感性分析侧重于研究专用泊位的租赁情况。选取每周泊位租赁费用、船舶在港单位时间运营成本、船舶在港单位时间装卸成本等参数对不同班轮公司租赁专用泊位策略以及3种成本的影响进行敏感性分析。选取“40-200-4”规模的算例进行分析,4 家班轮公司分别拥有20,20,80,80 艘船舶,灵敏度分析结果如图4 和图5所示。
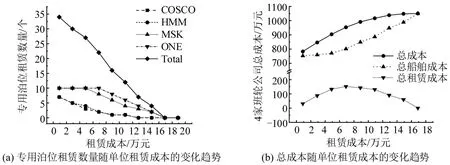
图4 各公司租赁专用泊位策略与成本随泊位租赁成本的变化Fig.4 Dedicated berths leasing strategy and cost of each liner carrier along with change of berth leasing cost
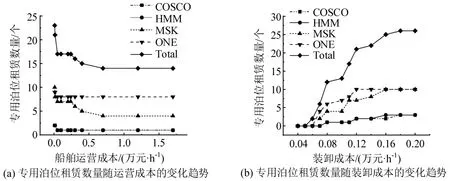
图5 各公司租赁专用泊位策略随船舶运营成本与装卸成本的变化Fig.5 Dedicated berths leasing strategy of each liner carrier along with change of operating cost and handling cost
从图4(a)可以发现,各个班轮公司租赁专用泊位的数量随单个泊位租赁成本的上升而下降;且船队规模较大的MSK 和ONE 租赁专用泊位的数量多于规模较小的HMM 和COSCO,体现规模越大的班轮公司倾向于租赁更多的专用泊位。从图4(b)可以发现,随着单个泊位单位时间租赁成本的增加,班轮公司总的租赁成本先增后减。在单个泊位的每周租赁成本为6.9 万元时,港口运营者可以得到最大的专用泊位租赁费用。
从图5(a)可以发现,随着船舶运营成本的增加,各班轮公司租赁专用泊位数量总体呈现下降趋势。主要原因在于,随着船舶运营成本的增加,BAP模型的目标函数倾向于所有船舶尽快离港,所以班轮公司不宜租赁过多专用泊位。当船舶单位运营成本在0~500 元·h-1范围内增长时,船舶运营成本的增加会导致泊位租赁数量的减少。从图5(b)可以发现,随着装卸成本的增加,各班轮公司租赁专用泊位的数量增加。主要原因在于,班轮公司的船舶在专用泊位的装卸成本较低,因此单位装卸成本越高,班轮公司越倾向于租赁更多的专用泊位来避免高额的装卸成本。
4 结论
本文研究了考虑到港船舶属于不同班轮公司的混合泊位分配与专用泊位租赁的联合优化问题,通过基于实际港口数据的算例测试,得出如下结论和启示:
(1)不同班轮公司会根据自身的船队规模租赁数量合适的专用泊位,规模越大、船舶到港时间越集中的船公司有租赁更多专用泊位的倾向,港口应调查到港船舶所属班轮公司的船队规模以便于进行泊位规划。
(2)当班轮公司租赁合理数量的专用泊位时,可节约20%~30%的运营成本。港口在实现降低成本增加收入的同时也需要考虑港口拥堵导致等情况的发生,港口需要为专用泊位配置装卸效率更高或数量更多的设备,以提高装卸效率,进而加快港口船舶在专用泊位的周转。
(3)本文构建MBAP-L 模型的优化结果表明,班轮公司会优先使用专用泊位,但在港口拥堵时不会只使用专用泊位,也会使用普通泊位进行靠泊装卸作业。因此,港口应合理限制班轮公司租赁专用泊位的数量,避免部分班轮公司过度租赁影响其他公司的到港船舶靠泊。
(4)在本文算例规模和成本取值的前提下,港口制定6.9 万元的租金可收取最多租赁费用,此时有55%的泊位被租赁。港口在与班轮公司签订专用泊位使用合同时,要根据实际市场情况,考虑到船舶平均在港时间与营收之间的平衡,制定合理的专用泊位租赁费用,并出租合理数量的专用泊位,才能在获利的同时吸引班轮公司租赁专用泊位。
