道路环形交叉口机动车冲突风险区识别模型研究

2024-03-03胡立伟张瑞杰赵雪亭贺雨陈琛刘冰侯智

交通运输系统工程与信息 2024年1期

胡立伟，张瑞杰，赵雪亭，贺雨，陈琛，刘冰，侯智

(昆明理工大学，交通工程学院，昆明 650500)

0 引言

无信控环形交叉口作为一种特殊的平面交叉口，具有一定的自组织性。在交通需求较小的情况下，它能使进入交叉口的直行和左转车辆绕岛沿逆时针方向前进，化车流冲突点为交织点，从而在一定程度上降低交通冲突和事故的发生率，提高车辆的行车安全。然而，随着我国经济的快速发展，许多环形交叉口的承载能力已经难以满足城市快速增长的交通需求，特别是在高峰时段由于环内交通量过大、合分流交织区过短以及弯道线性条件的复杂性，使得环内交通环境复杂，车辆加减速和换道操作频繁，驾驶员容易对安全车速、车距产生错误判断及操作，从而产生行车风险，引发交通事故。因此，准确地识别无信号环形交叉口的机动车冲突区域，对于提高环形交叉口车辆的运行安全具有重要的意义。

目前，国内外学者主要从几何设计、信号配时设计、交通流特性、机非冲突、不同类型交叉口安全性能差异性以及驾驶行为等几个方面对环形交叉口的安全性评价和改善措施进行研究，并构建相应的评价体系与优化方法。几何设计方面：潘兵宏等[1]提出一种新型立体环形交叉口，以提高交叉口的通行效率和行车安全；Keisuke Yoshioka等[2]以入环车辆对环内行驶车辆的不可见概率和碰撞冲击力为基础建立环形交叉口几何设计安全性的评价指标。信号配时设计方面：柴婷婷[3]以冲突特性为切入点，提出基于冲突分析的环形交叉口信号配时参数计算方法。交通流特性方面：成卫[4]在研究环形交叉口入口处到达混合交通流冲突特性的基础上，建立了城市2 车道与3 车道环形交叉口混合交通流条件下的通行能力模型；Aleksandra Deluka Tibljaš等[5]在微观仿真模型的基础上，分析无人驾驶汽车和常规车辆在不同构成比例下对环形交叉口安全水平的影响。机非冲突方面：张栋[6]通过提取机动车和电动自行车运行轨迹，分析驾驶人与骑行者在环形交叉口处发生冲突的机理以及冲突分布情况。在各类型交叉口安全性能评价方面：Prakash Ranjitkar[7]的研究表明，对于行车效率和安全性能来说，环形交叉口仅在中等交通量需求下比信号交叉口表现更好，而在高交通量需求下，信号交叉口通常比环形交叉口表现更好；林雨平[8]以冲突率为评价指标，利用模糊综合评价方法对多个信控环形交叉口整体交通安全状况进行评价。驾驶行为方面：刘擎超等[9]对环形交叉口场景下人工接管智能汽车过程中的事故风险进行探究，结果表明，速度是致使环形交叉口内车辆接管过程事故率发生的重要因素，且交叉口入口区域的车辆接管行为的事故率要明显高于环道区域。另外，目前交通冲突技术的研究大多数应用在常规交叉口[10]，公交站台[11]，出、入口匝道[12-14]以及急弯路段[15]等交通场景下，而环形交叉口在物理结构和运行规则上与之都不相同，交通流特性和交通冲突特点与上述交通场景存在较大差异，因此有必要对环形交叉口内部具体的冲突易发区域进行更加深入的研究。

鉴于此，本文基于交通冲突技术对环形交叉口的交通冲突特性与规律进行研究，探讨环形交叉口冲突风险区域识别方法。首先，以昆明国际会展中心环形交叉口为调查对象，利用无人机拍摄工作日早、晚高峰和平峰交通流视频，并借助Kinovea软件对航拍视频进行预处理，构建本次研究的数据库；然后，基于避险行为和交通冲突评价指标TTC对交通冲突风险严重性进行判别，从而构建环形交叉口机动车冲突风险识别模型；最后，以数形结合的方式直观地分析环形交叉口内交通冲突分布特性，并对36 个子区段的冲突风险等级进行评定，以期对环形交叉口安全水平的提高作参考。

1 数据采集及预处理

1.1 数据采集地点和时间

为获取城市无信控环形交叉口的交通流状态数据以及交通冲突数据，本文选取云南省昆明市国贸路—海明路环形交叉口作为研究对象，其相交道路中国贸路方向(东西方向)为双向6 车道，海明路方向(南北方向)为双向4 车道，环形交叉口内部为3 个环道，路面均为沥青混凝土路面。数据采集时间为2023年3月1日早高峰8:00-8:30，平峰10:00-10:30，晚高峰16:00-16:30，天气晴朗。环形交叉口数据采集现场及几何构造示意图如图1所示。

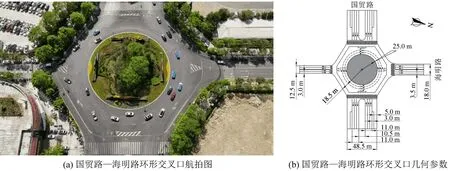
图1 数据采集现场及几何构造示意图Fig.1 Schematic diagram of data collection site and geometric structure

1.2 数据获取及处理

1.2.1 数据获取

本次实验使用如图2(a)所展示的大疆御3无人机，其具备宽视野、长航程和高分辨率的特点。通过GPS(Global Positioning System)定位，无人机在距离地面约100 m的高度静止悬停拍摄，覆盖范围为长600～700 m，宽300～350 m。所拍摄的视频精度达到了0.2 m，满足车辆数据采集要求。无人机最长飞行时间为40 min，支持4 K/60 P的视频录制分辨率。相比传统的数据采集方式，无人机视频拍摄可以采集环形交叉口内所有车辆的数据，便于识别车辆轨迹，连续性较好。

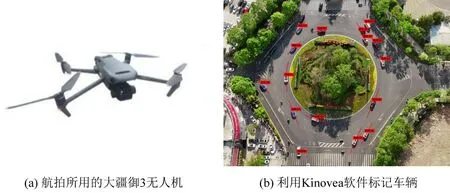
图2 航拍设备及Kinovea软件处理车辆轨迹操作界面Fig.2 Aerial photography equipment and Kinovea software processing vehicle trajectory operation interface

1.2.2 数据处理

本文使用如图2(b)所展示的Kinovea视频运动分析软件解析实验拍摄的视频，以环岛中心为原点建立平面直角坐标系，每7帧输出一次区域内所有车辆的实时轨迹坐标(x,y)、车辆ID、速度、加速度、车辆绕环岛中心转过的弧度θ，并将识别结果保存下来以供后续进行冲突风险评估。视频识别结果如表1所示。

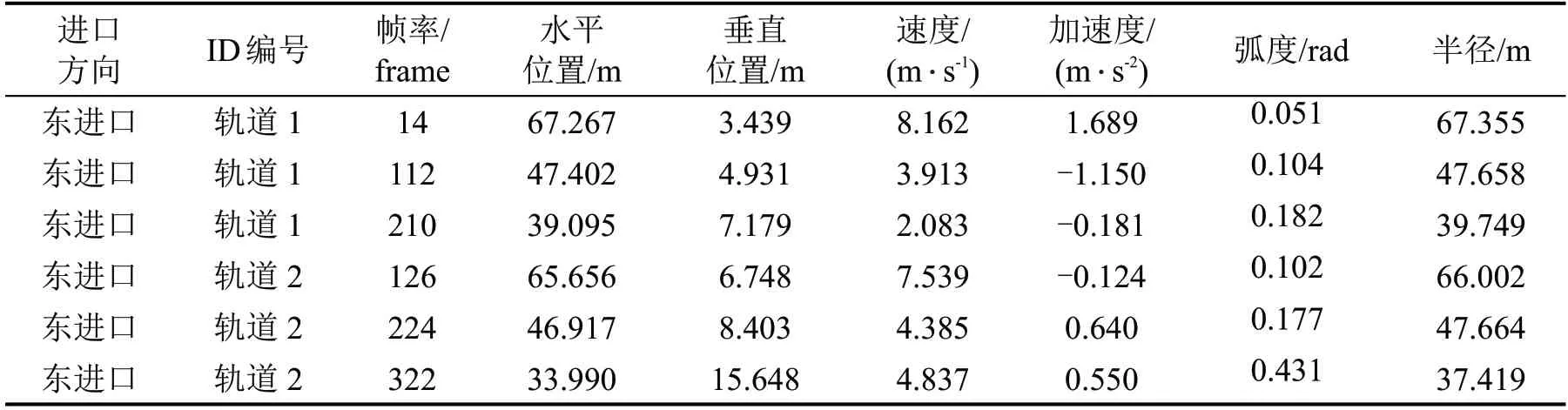
表1 视频识别部分结果Table 1 Video recognition partial results

2 机动车冲突风险区域识别模型构建

2.1 冲突风险预判定

为提高工作效率，对无人机拍摄的视频进行冲突预判至关重要。在环形交叉口内行驶的车辆发生冲突时，可能出现以下情况：

(1)入环车辆礼让环内车辆导致减速或停车；(2)环内车辆礼让入环车辆导致减速或停车；(3)出环车辆礼让前方出环车辆导致减速或停车；

(4)外侧环道车辆礼让内侧环道车辆变道出环导致减速或停车；

(5)环内后车礼让环内前车变道出环导致减速或停车；

(6)环内车辆出环导致转向行为；

(7)环外车辆入环导致转向行为等。

根据避险行为原则，当两辆车可能发生碰撞时，至少一方会采取加减速、停车或改变轨迹的行为。因此，当加速度的绝对值大于4 m·s-2或运动方向变化大于30°时，则认定目标车辆存在避险行为。通过对冲突风险进行预判，可以剔除正常行驶车辆的轨迹数据以减少工作时间。

2.2 直线路段车辆TTC计算

本文主要关注环形交叉口内冲突点的分散情况，而后侵入时间(Post Encroachment Time,PET)是用来计算前后两辆车到达某一给定位置的时间差，并不能直接用于找寻冲突点的位置，因此本文选用碰撞时间(Time to Collision,TTC)作为环形交叉口交通冲突的判别指标。通过利用TTC 来评估车辆在发生避险行为时驾驶员的避险能力。TTC 值越小，表示避险时间越短，发生事故的概率越高。在水平直线路段，TTC的计算公式为

式中：STTC为第i辆车碰撞到第i-1辆车的时间(s)；xi-1(t)、xi(t)为前车i-1 与跟随车辆i在t时刻时，直线路段的坐标位置(m)；vi-1(t)、vi(t)为前车i-1与跟随车辆i在t时刻的瞬时速度(m·s-1)；li-1为前车i-1的车长(m)；Li_i-1为两车的位置差(m)。

2.3 环形交叉口车辆TTC计算

直线路段TTC 算法是假设前后车辆在某一时刻保持当前的运动方向和速度不变，直到发生碰撞。然而，在环形交叉口中，车辆沿着中心环岛曲线行驶，导致车辆的运动方向不断变化。这就使得直线路段TTC 算法不能准确应用于环形交叉口场景。

如图3(a)所示，如果前后车辆位于同一环道上，意味着在任何时刻两车沿着切线方向继续作直线运动永远不会相交，导致直线路段TTC算法无法找到冲突点，进而无法计算得出TTC 值；如图3(b)所示，如果前后车辆位于不同环道上并且由于前车或后车的换道行为导致即将发生碰撞时，使用直线路段TTC算法虽然可以找到两车运动轨迹的交点，但所得的冲突点位置与实际冲突点存在较大偏差，并且该冲突点不在两车轨迹线之间。图3中，Vi-1、Vi为前车i-1与跟随车辆i在将要发生碰撞时的瞬时速度(m·s-1)；为两车绕环岛中心作圆周运动所对应的半径平均值(m)。

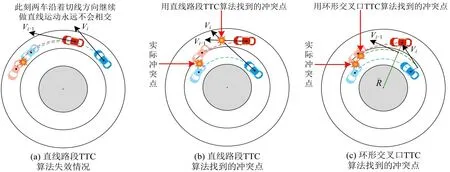
图3 环形交叉口TTC算法相对于直线路段TTC算法的优势Fig.3 Advantages of roundabout TTC algorithm over straight section TTC algorithm

为应对环形交叉口道路线形的特殊性，本文提出一种改进的环形交叉口车辆TTC 计算方法，如图3(c)所示。该方法假设前后车辆沿着轨迹平均半径计算得到的同一圆弧运动，只要后车的速度大于前车，就会存在冲突点，并且该冲突点位于两车运动轨迹线之间。这一改进使得TTC 计算更符合实际两车发生冲突时的运动轨迹情况，从而提高了TTC计算的精确性。改进后的TTC计算公式为式中：Ri-1(t)、Ri(t)为前车i-1 与跟随车辆i在t时刻绕环岛中心作圆周运动所对应的半径(m)；θi-1(t)、θi(t)为前车i-1 与跟随车辆i在t时刻绕环岛中心转过的弧度(rad)；vi-1(t)、vi(t)为前车i-1 与跟随车辆i在t时刻的沿运动轨迹切线方向的瞬时速度(m·s-1)；li-1为前车i-1 的车长(m)；R_为两车绕环岛中心作圆周运动所对应的半径平均值(m)；Δθ为两车的弧度差(rad)。环形交叉口TTC算法示意图如图4所示，其物理变量同上所述。

图4 环形交叉口区域的TTC计算Fig.4 TTC calculation in roundabout area

3 冲突风险严重性判别及冲突风险统计

3.1 冲突风险严重性判别

由于环形交叉口相较于直线路段具有更高的交通动态性和信息密度，故两者的TTC阈值有所差异。为提高本文结论的可信度，采用累积频率曲线法确定TTC 的阈值。累积频率曲线法是交通工程中常用的统计分类方法，可用于确定道路的限速值。该方法基于实测速度数据构建累积频率曲线，并利用曲线上与限速对应的百分位数来确定最低限速、中位车速和最高限速。类似地，可以运用累积频率曲线法来确定环形交叉口交通冲突事件的严重程度。本文选择早、晚高峰和平峰各20 min的数据采集片段，利用2.3 节所述方法计算环形交叉口TTC值。将计算得到的TTC数据以0.2 s为间隔进行分组，并绘制TTC的累积频率曲线，按照15%、50%和85%位累积频率对应的TTC 值作为严重冲突、一般冲突和轻微冲突的划分标准，如图5所示。

图5 车辆TTC帕累托图Fig.5 Pareto diagram of vehicle TTC

由图5 和表2 可知，15%、50%、85%分位对应TTC区间分别为(1.2，1.4]s，(2.8，3.0]s，(4.4，4.6]s。因此，当TTC 值处于(0.0，1.2] s 时，为严重冲突；当TTC值处于(1.2，2.8]s时，为一般冲突；当TTC值处于(2.8，4.4] s 时，为轻微冲突；当TTC 值处于(4.4，6.0]s 时，视为无效冲突。具体冲突风险严重程度阀值划分如表3所示。

表2 车辆TTC累计频率分布Table 2 Accumulated frequency distribution of vehicle TTC

表3 环形交叉口机动车冲突风险严重程度划分Table 3 Severity classification of motor vehicle conflict risks at roundabouts

3.2 冲突风险数统计

通过以上划分标准，对仅存在交通干扰的现象进行剔除，确定受调查环形交叉口内共存在交通冲突个数为1700 个，其中严重冲突为301 个，占比17.71%；一般冲突为646个，占比38.00%；轻微冲突为753个，占比44.29%。各个采集时段内交通量和交通冲突数统计如表4所示。

表4 各时段交通量、交通冲突数统计Table 4 Statistics of traffic volume and number of traffic conflicts at different time periods

4 交通冲突风险时空分布及风险等级划分

4.1 空间结构划分

为深入分析环形交叉口区域内交通流特性和交通冲突空间分布，首先，以环岛中心至海明路以北方向的车道中心线为起点，沿逆时针方向将整个环形交叉口划分为36 个子区段，每个区段的角度间隔为10°。这样的划分方式既避免了区段过大或过小导致交通流和冲突特性变化不连续，也便于进行后续的统计和图形展示。接下来，根据车辆的运行规律，将这36个子区段组合成4个大区段。具体的组合方式为：第Ⅰ区段由1～9 子区段组成，第Ⅱ区段由10～18 子区段组成，第Ⅲ区段由19～27 子区段组成，第Ⅳ区段由28～36子区段组成。每个大区段都经历了合流段、交织段和分流段的过程。这种组合方式能够更深入地研究交通冲突特性在不同阶段的演变规律，揭示环形交叉口内部交通冲突的动态变化。通过以上的划分和组合方法，建立环形交叉口的结构化框架，有助于进一步准确定位交通冲突聚集点。具体划分情况如图6所示。

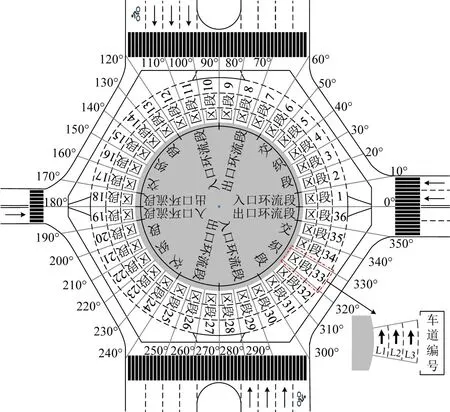
图6 环形交叉口区域划分Fig.6 Division of roundabout areas

4.2 环形交叉口交通冲突风险时空分布规律探究

通过视频识别输出的轨迹数据，可以计算出车辆之间发生碰撞前的时间间隔(最小TTC值)，再结合发生碰撞前对应帧数下两车的速度、绕环半径、位置关系和最小TTC值，可以反推出两车预计轨迹相交冲突点Q的坐标位置。然后，利用3.1 节计算的冲突严重性阈值判别识别到的各个冲突点的冲突严重性，从而直观准确地得出环形交叉口不同类别交通冲突的空间分布规律，车辆轨迹冲突点具体计算流程如图7所示。本文对比分析了3个时间段的交通冲突空间分布图，如图8所示。

图7 车辆轨迹冲突点计算流程图Fig.7 Vehicle trajectory conflict point calculation flowchart

图8 各时段交通冲突空间分布Fig.8 Spatial distribution of traffic conflicts at different time periods

根据图8可以观察到：该环形交叉口的交通冲突分布呈现一定的潮汐特性，即在早高峰时段，西向东方向的交通冲突点数量与分布情况与晚高峰时段的东向西方向的交通冲突点数量与分布情况大致相当；在第2～6 区段、第13～17 区段、第20～24区段和第31～35区段，交通冲突明显比其他区段更为集中，表明这些区段是该环形交叉口的事故频发区域。此外，在该环形交叉口的东、西进出口斑马线附近，交通冲突较为集中的原因是横向通行的行人数量较多，车辆会频繁停车让行，导致后续车辆多次制动，增加交通冲突的发生。另外，尽管该交叉口南进出口方向的交通量不大，但仍然存在大量的交通冲突，这是由于一些车辆在该方向的出入口附近违规停车，导致外侧车道被侵占，路面变窄，迫使车辆在进出口时不得不逆行通过，引发交通拥堵。因此，对该交叉口的安全改进应重点关注上述区段，特别是需要解决南进出口方向的违规停车现象。

为进一步研究交通冲突在环形交叉口的空间分布，量化交通冲突，分别统计早、晚高峰及平峰时段每一区段的交通冲突次数和严重交通冲突率(即严重交通冲突数与冲突总数之比)。由图9可知，第17区段总的交通冲突数最多，第24区段和第6区段次之，交通冲突次数在每一个大区段上呈现先增加后减少，再增加再减少的变化规律，如早高峰时段交通冲突次数在第1～4 区段先增加再减少，第5～9区段再增加再减少。

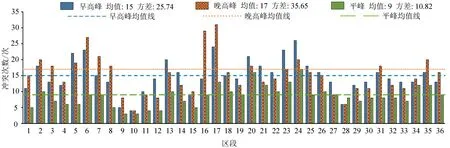
图9 分区段交通冲突数统计Fig.9 Statistics of traffic conflicts in different sections

由图10可知，在第3～5区段、第14～16区段、第21～23 区段、第32～34 区段的严重交通冲突率处于高位递增的趋势，其中早高峰时段第16 区段和第23区段的严重交通冲突率最高约为35%，是该环形交叉口事故高危区域。此外，还比较了高峰时段和平峰时段的交通冲突情况，在高峰时段某一子区段上交通冲突的平均发生次数约为15 次，严重冲突的平均发生率为17.45%；在平峰时段某一子区段上交通冲突的平均发生次数约为8次，严重冲突的平均发生率为8.28%。结果显示，高峰时段的交通冲突相比平峰时段更为严重，高峰段的交通冲突和严重冲突发生率约为平峰段的2倍。

图10 分区段严重冲突率统计Fig.10 Statistics on severe conflict rate of partition segments

4.3 区段交通冲突风险等级评定

根据环形交叉口各区段的交通冲突数和严重交通冲突率，可以评估每一区段的交通冲突风险等级。综合考虑早高峰、平峰和晚高峰的交通冲突数据和严重交通冲突率，利用均值法得出该环形交叉口在每一区段上的综合交通冲突次数为13 次，综合严重交通冲突率为14.28%。基于这两个阈值，可将区段的风险划分为4个等级，具体如表5所示。

表5 区段风险等级评判依据表Table 5 Evaluation basis table for section risk level

TTC是一种描述事故接近程度的时间度量值，TTC值越小，事故风险程度越大，当TTC值为0时，则可认为事故已经发生。因此，本文通过对不同冲突严重程度的阈值取倒数作为风险值，将4.2 节得到的交通冲突点绘制成三维风险值热力分布图，如图11 所示，并将其与各区段风险等级判定结果图对照，如图12所示。

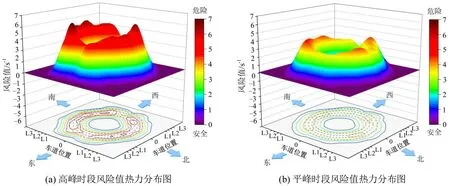
图11 平高峰三维风险值热力分布图Fig.11 Thermal distribution map of three-dimensional risk values during normal and peak periods

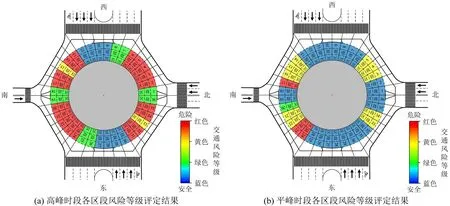
图12 平高峰各区段风险等级评定结果Fig.12 Risk level assessment results for different sections of flat and peak periods

对图12 中平峰、高峰时段环形交叉口风险等级评定结果进行整理，可得到如表6 所示的统计结果。

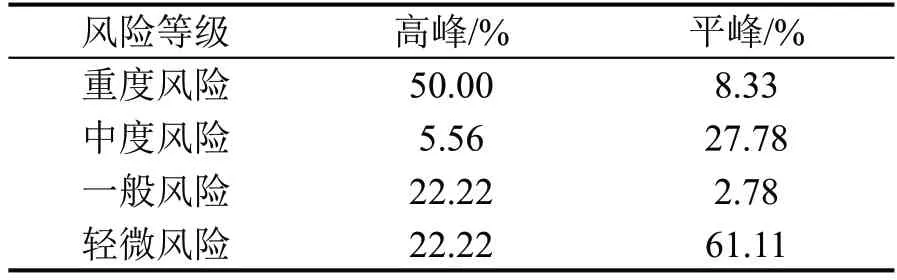
表6 平高峰不同风险等级对比Table 6 Comparison of different risk levels during normal and peak periods

根据研究结果分析可得，环形交叉口在高峰时段更容易发生交通事故。此外，不论是高峰时段还是平峰时段，第17、23和24区段的风险等级都一直维持在重度风险，这意味着这些区段存在持续且顽固的交通安全风险。另外，根据图11可知，风险值较高的区域主要集中在出口至入口的交织区段，尤其是西南和东南方向的交织区段，这两个区域的亮点区域最强也最大。与此相对应，风险值较低的区域则主要出现在环流段上，与图12 中环形交叉口各区段风险等级评定结果一致。