考虑载客状态的改进孤立森林浮动车异常数据检测算法

2024-03-03任其亮徐韬刘媛程龙春

交通运输系统工程与信息 2024年1期

任其亮，徐韬*,，刘媛，程龙春

(1.重庆交通大学，重庆 400074；2.重庆设计集团有限公司，重庆 400050)

0 引言

浮动车数据(Floating Car Data,FCD)因其覆盖范围广、时效性高等特点，已成为城市交通大数据挖掘与分析的重要基础数据，并广泛应用于道路车速预测[1]、瓶颈识别[2]等智能交通应用领域。FCD采集分析技术因多场景的应用范围使其拥有很强的挖掘和应用价值，但是大量技术问题，例如，设备故障、信号遮蔽、传输失真或其他因素影响，会引发千万数量级的FCD 出现无法避免的异常或失真数据，为了确保动态交通数据信息的有效性和精准性，准确、实时的异常数据检测和处理是不可或缺的。

现有异常检测方法主要对由浮动车车速组成的一维时间序列进行直接处理，存在信息挖掘不足、检测精度不高等问题。未能检测出的异常数据会污染数据源，导致数据分析结果误差较大或失真，从而降低FCD 数据挖掘和分析效果。根据异常数据样本分布不同，异常数据可分为单点异常、上下文异常和群体异常这3类，FCD主要表现为单点异常和上下文异常。根据检测方法模型特性的不同，现有异常数据检测方法可分为基于数理统计方法、空间相似度方法(距离、密度)、集成学习、深度学习这4类。许伦辉等[3]根据前后速度差识别异常数据再利用动态时间规划方法进行数据修复，但对连续多个异常数据识别较弱；郑启晨[4]利用经纬度阈值法和瞬时速度阈值法从空间轨迹视角对离群GPS(Global Positioning System)数据点进行识别，但无法识别出速度突变异常点；吴艳平等[5]根据浮动车运行轨迹从空间匹配出发对偏离样本数据进行检测并重构轨迹序列，但仅适用于GPS坐标异常类型的数据识别。可见数理统计方法和空间相似度方法适用范围有一定的局限性。

由于FCD 数据缺少样本标签信息，更适应于无监督学习方法，因此，近年来大量学者利用集成学习、深度学习方法开展异常数据检测。曹鹏等[6]利用K-means 聚类算法对浮动车停放和等待时的异常数据进行识别，Lam等[7]利用朴素贝叶斯和高斯混合模型对交叉口离群FCD 数据进行检测，Li等[8]通过高斯过程回归器识别出异常FCD 数据并估计路网交通量，Hu等[9]通过聚类算法对浮动车在交叉口转弯时的异常数据进行检测，检测准确率为85.0%。相关算法在其他领域异常数据检测中得到了大量应用，陈滢生等[10]提出基于自编码器的大数据集异常数据识别算法，并利用小波去噪进行预处理，但会损失部分价值信息；牛罡等[11]利用传统IForest 对电力数据进行异常检测，但收敛速度较慢；张万旋等[12]提出IForest 动态更新策略，开展液体火箭发动机异常检测，但无法避免更新样本对模型参数污染问题；孙朝云等[13]提出基于D-S-LOF(Difference-Summation-Local Outlier Factor)的道路环境感知数据检测方法，构建由一阶减法前向差分、相邻两项求和的二维特征向量，再利用局部异常因子(Local Outlier Factor,LOF)算法进行检测，但容易陷入局部最优，不适用于具有全局特征的FCD数据检测；唐立等[14]提出动态生长高度的改进IForest算法，但数据维度偏低，检测准确度有待提高。

综上，目前流行的集成学习方法如IForest因具有高维数据全局性和鲁棒性[15]特点，适合FCD开展异常数据检测应用，但当前IForest算法在动态检测中存在新样本对模型污染和收敛性能不足等问题，且现有研究鲜有考虑载客和未载客不同运营条件下车辆驾驶行为差异对数据干扰的影响，需要提高数据维度充分挖掘数据信息，并分析不同载客状态下模型适应能力，提高异常数据检测精度和处理能力。基于此，本文通过差分等方式扩展原始数据维度，并在IForest基础上提出差额累计更新和动态区分辨识的改进IIForest 算法，对FCD 异常数据进行检测，同时对不同载客状态异常数据分布特点进行对比分析，最后通过重庆市中心城区道路数据进行验证，以证明该组合算法的有效性和适应性。

1 问题描述

每辆装有GPS的浮动车(如出租车、公交车等)每10～15 s返回一条样本数据，样本字段包括日期、时间片段、公司代码、车牌ID、经度、纬度、车速、方向角、载客状态共9个字段。设城市道路网络共含有n条路段，所需检测路段为lj,j∈[1,n]，将样本数据中经度、纬度信息匹配至城市GIS(Geographical Information System)路网中路段lj，统计出位于lj经度、纬度坐标内的样本数据，按时间片段数值进行升序排列，排列后的车速字段数据汇总形成原始数据集合y，即

式中：i为样本索引，i∈(1,m)；m为样本总条数；yi为原始数据集合的异常数据值，yi∈y。

则本文定义的浮动车数据异常检测算法任务为：在已知原始数据集合y的前提下，识别检测出目标路段lj中存在数据异常值yi，为后续异常数据修复和填补提供基础。

2 基于S-DTA-IIForest的浮动车数据异常检测算法

根据交通流理论，无论是连续流还是间断流，交通流参数在时间上存在一定的连续性，当时间序列中某一时刻数据存在突变点或空值等异常值时，通过前后两项的差分运算可快速识别出异常点；然而当出现两个及以上呈现递增或递减的连续异常值时，前后差分值则不会发生明显变化，也就无法检测数据的异常点。本文在借鉴前后差分的基础上，构建高维向量数据集，利用IForest 无监督学习方式从高维向量数据集中进行采样，训练出孤立树并记录路径长度，计算出样本测试集异常得分，进而检测出数据异常点。

(1)建立S-DTA高维特征向量

孙朝云等[13]提出一种D-S 二维特征向量构建方法，虽然增加了数据维度，但在处理多个连续异常值时不敏感。因此，借鉴D-S前后差分与求和思想，构建由相邻两项求和(S)、三阶求和平均差分(DTA)组成的二维度空间特征向量，设数据集y={y1,…,yi,…,ym}中yi为第i个样本数值，若yi为异常点，则二维特征向量会出现一个离群点，即(Si,DDTA,i)，Si为第i个样本求和特征值，DDTA,i为第i个样本三阶求和平均差分特征值，各特征值表达形式为

(2)改进IIForest算法

IForest 基本思想是异常样本更容易快速落入叶子结点，即异常样本在决策树上距离根节点更近。IForest算法不是筛选出正常样本数据，而是孤立出异常数据，IForest算法通过递归地随机分割数据集，直到所有的样本点都是孤立的，在这种随机分割的策略下，异常点通常具有较短的路径，相较于LOF、K-means 等传统算法，IForest 算法对高维数据有更好的鲁棒性。IForest 算法需构建孤立树iTree，通过二叉搜索树结构来孤立样本，流程如下。

Step 1 选择样本数据集中n个数据作为训练集，训练集最大值、最小值分别为Xmax、Xmin，并放入一个二叉树BTree 中。

Step 2 选择样本数据集中任意维度ki和切割点Q(Q∈(Xmin,Xmax))，将ki维度下小于Q的样本数据划分到左节点，余下数据划分到右节点。

Step 3 在下一子节点以递归方式重复Step 1和Step 2，直到每个节点只有一个样本数据或达到设置的树最大高度。

Step 4 选取下一个BTree，重复Step 1～Step 3，并训练完成所有BTree。

Step 5 计算每个iTree 平均路径长度c(n)，归一化算式为

式中：H(n)为调和数；n为用于生成单颗孤立树的样本点数量；ζ为欧拉常数，ζ≈0.58。

Step 6 计算异常值分数s(x,n)，算式为

式中：hi(x)为样本点x在孤立树i中的深度值；t为孤立树数量。

s(x,n)越接近1，表示该点为异常点的可能性越高；s(x,n)越接近0，表示该点为异常点的可能性越低；若s(x,n)接近于0.5，则该点可能为正常点或异常点。

传统IForest算法主要存在两个问题：一是在动态数据检测下随着样本点P的不断加入，由多个孤立树组成的孤立森林会计算出样本点异常值分数并改变模型结构，导致模型被异常数据污染；二是每个孤立树的异常数据检测能力有差异，导致算法收敛速度存在差异。为解决上述问题，本文提出差额累计更新和动态区分辨识的改进IIForest(Improvement IForest,IIForest)算法，对于问题一，本文提出停止阈值σ，当新样本点异常值分数s大于σ时，仅检测新样本，不更新孤立森林模型；对于问题二，则计算每个二叉树BTree 的区分辨识度β，β处于设定停止区间时，则停止生长，以此提升算法收敛性能。关键改进步骤如下。

Step 1 根据所建立的孤立森林模型，计算新样本点P的异常值分数s。若s>σ，则只输出s并进行判定；若s≤σ，则重新训练孤立树iTree 并更新孤立森林模型。

Step 2 统计传统IForest 算法Step 2 中，随机ki维度下切分点Q左侧集合的数据样本数量NL和右侧数据样本数量NR。

Step 3 对该节点区分辨识能力进行判定。根据IForest算法原理，若该节点能有效区分正常点和异常点，则该节点为高辨识节点，可继续生长；若该节点无法区分正常点和异常点，则该节点为低辨识节点，应结束生长，并选择下一个BTree 进行训练。区分辨识能力由区分辨识度β参数标定，即

式中：β∈(a,δ)时，则认为左右节点样本数量差异较小，该节点为低辨识节点，停止生长，其中，α、δ为上下区间值；ε为偏离系数，ε∈(0.5,1.5) 。本文ε=1，α、δ分别为0.8、1.25。

Step 4 重复Step 2～Step 3，并训练完成所有BTree，按照传统IForest中Step 6计算异常值分数。

Step 5 根据异常值分数，判断该点是否为异常点。

本文IIForest算法能解决新加入异常点样本对孤立森林模型的污染问题，同时识别出节点的辨识能力，有效减少非必要运算量，缩短算法运行时耗，提高模型收敛速度。

3 实验与结果分析

实验环境为Intel(R)Core(TM)i7-10875H CPU 2.30 GHz，内存32 G，Windows 10 专业版操作系统，本文所涉及到的算法均使用Python 软件中的Numpy、Pandas及Sklearn库实现。

3.1 浮动车数据集构建

本文收集的数据集为重庆市中心城区2022 年7 月15 日12:00-12:15 浮动车(出租车)GPS 数据，样本总条数为299153条，其中经纬或纬度为0的明显错误数据6507 条，错误率为2.18%，因样本数据集中在内环快速路以内区域，选取学府大道R1 作为测试路段，具体如图1所示。

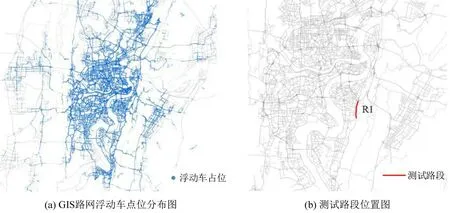
图1 样本数据分布示意图Fig.1 Sample data distribution diagram

3.2 评价指标选取

结合混淆矩阵定义，检测结果可分为真阳性(True Positive,TP)、真阴性(True Negative,TN)、假阳性(False Positive,FP)、假阴性(False Negative,FN)这4 类。为评价不同模型异常数据检测效果，选择AUC、F1-score指标进行评价。

(1)AUC

AUC是ROC(Receiver Operating Characteristic,ROC)曲线下的面积，ROC横坐标为假正率FPR，纵坐标是真正率TPR，AUC ∈[0,1]，AUC 越大，模型检测准确率越高。

(2)F1-score

F1-score 是精确率Precision (P) 和召回率Recall(R)的加权调和平均值，用以衡量模型检测精度，F1-score越高，精度越理想。

式中：F1-scroe为F1-scroe的值；TP为预测正确答案的频数；FP为将其他类标签预测为本类标签的频数；FN为本类标签预测为其他类标签的频数。

3.3 结果对比与分析

(1)建立二维特征向量

R1 有效样本条数为1100 条，车速时间序列数据如图2 所示，“车速”字段中最大值Max_speed 为74 km·h-1，最小值Min_speed 为0，与空值“null”相比，0 并不代表一定为异常值，即可能为等待信号灯、严重拥堵时静止状态下的车速真实值，简单删除0样本会导致分析结果失真，故需要通过智能学习算法识别出异常值。

图2 R1车速分布时间序列图Fig.2 Speed distribution time series diagram of R1

根据式(2)建立由S、DTA组成的特征向量数据集U，其中前900 个样本数据为训练集Utrain，余下200样本数据为测试集Utest。S-DTA特征向量图如图3(a)所示，可以看出，由于存在两个及以上连续车速为0的值，图中形成多个S为0的点，位于图像边缘侧。孙朝云等[13]提出D-S二维特征向量，由于连续多个0值，边缘形成“V”型图像点，难以进行识别，如图3(b)所示。

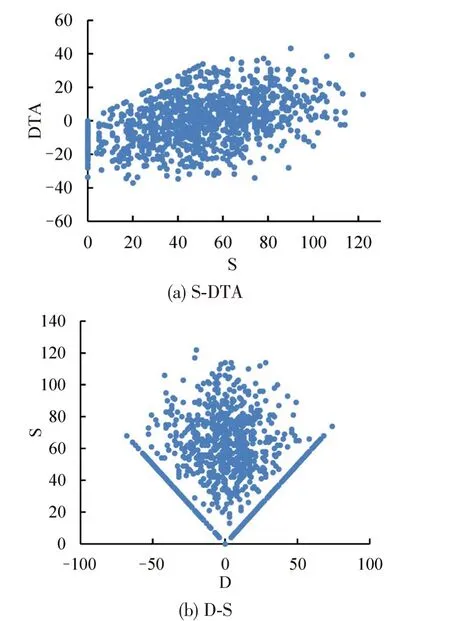
图3 二维特性向量图Fig.3 Two-dimensional characteristic vector map

(2)不同模型精度对比分析

设定本文IIForest 模型中各参数n_estimators为100，max_features 为2，contamination 为auto，max_samples 为256，bootstrap 为False，n_ jobs 为-1，random_state为1，将R1中Utrain作为训练集训练IIForest 模型，以测试集Utest用于测试模型精准度。还需确定停止阈值σ，当σ较大时，会导致部分被认为是“正常”点进而被用于更新模型；当σ较小时，会导致模型训练数据较少进而存在虚警风险，经过反复调试，当σ=0.47 时AUC 最大，故本文取σ=0.47。通过测试后，特征向量数据集U中正常点和异常点分布如图4所示。可见，异常值分布在二维特征向量散点图边缘，同时有效识别出车速连续0值中的异常点和正常点。

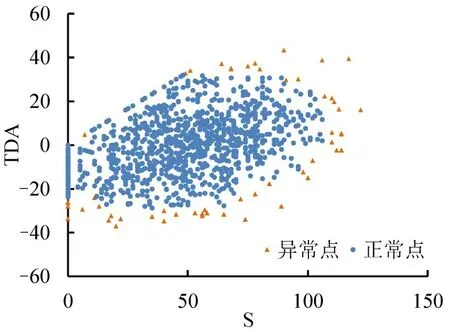
图4 S-DTA-IIForest异常检测结果Fig.4 S-DTA-IIForest anomaly detection results

为量化分析模型的准确性，在测试集Utest中新增人工标定“Label”字段，分为正常值“Normal”和异常值“Outlier”两种属性，以AUC、F1-score 指标对S-DTA-IIForest、S-DTA-Forest、T-Forest(传统时间序列)、D-S-Forest、D-S-LOF等5种模型进行对比分析，各指标如表1所示。

表1 模型检测结果评价Table 1 Detection result evaluation

本文S-DTA-IIForest模型AUC最大，为86.63%；S-DTA-IForest 模型次之，为85.51%；T-IForest 模型AUC 最低，仅为65.42%。F1-score 指标方面：S-DTA-IIForest模型最大，为0.89；S-DTA-IForest模型次之，为0.87；T-IForest 模型F1-score 得分最低，仅为0.70。表明经过原始时间序列经S-DTA 处理后，所构建的二维特征向量能增加模型对异常数据的辨识能力。此外，S-DTA-IForest模型运行时间为0.1151 s，较S-DTA-IForest模型0.1166 s减少0.0015 s，运行效率提高1.29%，收敛速度明显提升。

为分析S-DTA-IIForest 模型的参数适应性能力，基于R1 同一数据集，对参数max_samples、n_estimators等不同数值进行测试。当n_estimators为100 时，随着构建子树的样本数max_samples 增大，模型AUC 值出现波动，当max_samples 为500时，模型AUC 值最大，运行时间稳定在0.116 s 左右，max_samples 的增大并不会带来运行时间的大幅增长，如图5(a)所示；当max_samples=256 时，随着孤立树数量n_estimators 的增大，初期模型AUC值总体呈增长态势，n_estimators 大于100 后其AUC 值基本持平，但运行时间随着n_estimators 的增大呈线性增长，当样本数量较大时，模型运行耗时也显著增加，如图5(b)所示。因此，建议模型参数max_samples为500，n_estimators为100。

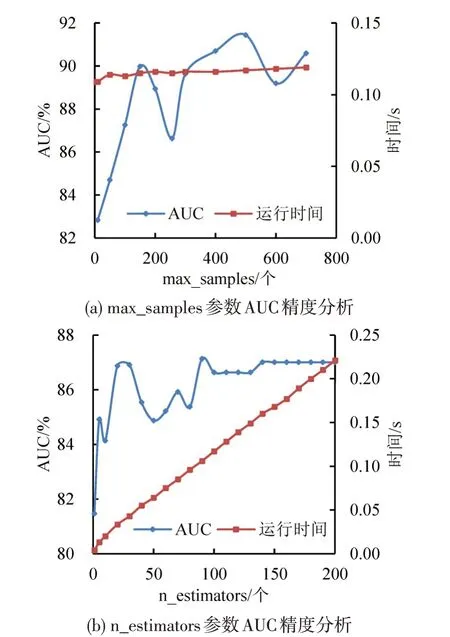
图5 模型不同参数适应性分析Fig.5 Adaptability analysis of different parameters in model

(3)不同载客状态下异常数据检测分析

利用S-DTA-IIForest 模型筛选出异常值后，浮动车数据异常点可分为空值点、突增点、突减点这3类，如序号1083和1084为空值点，呈现单个或多个连续0 值，实际中多为“null”空值数据；序号909 为突增点，表现为单个数据突然增加，随后急剧下降；序号1099为突减点，表现为单个数据急速下降，随后明显增加，具体如图6所示。

图6 S-DTA-IIForest模型浮动车异常值识别情况Fig.6 Identification of abnormal values of floating cars in S-DTA-IIForest model

原始FCD 数据“载客状态”为“0”表示未载客，“1”表示该车辆载客，Utest数据集中未载客样本数量为56条，占总数28.0%，载客样本条数144条，占72.0%。载客状态下，S-DTA-IIForest 模型AUC 为88.72%，较未载客82.35 提高7.7%，F1-score 为0.92，较未载客0.83提高10.8%，可见载客状态下模型精度更高，如表2所示。

表2 不同载客状态检测结果Table 2 Detection results of different passenger carrying states

从异常值分布看，Utest中异常点为10 个，异常率为5.0%，其中载客状态异常点为6 个，占60.0%，未载客状态异常点为4个，占40.0%，载客状态数据异常率为4.2%，未载客状态数据异常率为7.1%，未载客状态数据异常率较载客状态增大71.4%，即未载客状态数据的异常率更高，如图7所示。由于本文浮动车为出租车，在未载客时，驾驶员会频繁接单或时刻观察沿线是否有潜在顾客，车辆运行状态更易受到干扰，数据会存在一定波动，因此数据异常概率更高。