高斯函数拟合的地磁日变规律分析及改正

郭云飞，柴洪洲**，种 洋，汪金花，宿楚涵

(1.信息工程大学 地理空间信息学院，河南 郑州 450001；2.军事科学院，北京 100091；3.华北理工大学，河北 唐山 063210)

地磁场最初主要应用在地质研究和矿产资源的勘探过程，随着研究学者对地磁特性的不断探索，以及磁力仪和匹配算法的发展，地磁匹配定位的导航技术得到了发展应用.地磁场具有随时间和空间变化的时空特性[1-2]，地磁场的变化磁场主要成分是以一个太阳日为周期的太阳静日变化，而且在平静时期地磁静日变化是地磁测量过程中主要的误差来源[3]，变化范围大概从几个nT 到几十个nT 不等.吴迎燕等[4]通过台站实测地磁数据对地磁场的静日变化强度的季节性和长期变化进行了研究分析，结果表明其分量都具有相一致的11 年太阳活动周变化和长期变化，而且该台站数据波动变化显示其静日场强度梯度的剧烈扰动与太阳活动密切关联.在实测地磁数据采集工作中，时间相对较短，因此长期变化和季节变化对其影响相对较弱，主要变化场依然是以太阳日为周期的太阳静日变化，因此需要对地磁场的静日变化带来的影响通过日变改正进行校正.

地磁日变改正是地磁数据采集过程中的基础工作，是实现更高精度定位效果的重要前提，国内外研究学者对其进行了系列研究，提出了不同的日变改正方法以消除地磁日变化带来的误差影响.针对地磁太阳静日变化的影响，现行的磁静日日变改正主要是将日变站观测值减去该日变站改正基值作为某时刻的日变改正量[5]，通常采用平均值法、基时刻法或基时段法等实现日变站日变基值的求取.边刚等[6]提出基时刻或基时段法计算日变基值，同时建议采用取早晚时段平均值的基时段法处理磁观测数据.顾春雷等[7]根据多个地磁台获得的磁资料选用反距离加权法进行日变通化，证明该方法的有效性，同时也指出其插值精度与已知台站及待插值点的空间分布有关.李才明等[8]提出采用一个地磁平静日的日变观测数据，分时区进行加权平均确定日变改正的基值，通过对测定的日变曲线进行最小二乘圆滑降低仪器噪声，进行日变改正后的精度有所提高.杨震[9]尝试将经验模态分析方法应用于短期测量过程中求取日变基值.这些方法都只是把地磁日变站采集数据减去日变基值作为地磁日变数据进行地磁日变改正.也有学者针对日变改正问题采用函数模型以及统计分析等进行分析研究，其中Williams 等[10]将磁日变化视为磁测时间的相关函数并利用神经网络对其进行误差补偿；潘星辰等[11]在海洋磁测日变校正的研究中选用地磁台的长期观测数据，对地磁场日变随纬度变化规律进行分析，结果表明纬度改正方法能够更好地适应于远海磁测，为远海地磁台无法设立的问题解决提供了参考.也有学者采用自然正交分量分解法、分析统计法、全球地磁日模型，以及傅里叶级数分解法和小波变换等对太阳日造成的磁扰动部分进行分离，改进的日变改正精度有所提高，但是有时存在计算效率较低等问题[12-20].近距离日变观测资料的获取及日变改正将大大提高磁测精度[21]，目前的研究大都基于相对稳定的台站数据进行分析和总结，对于实际应用中的区域地磁数据采集及日变改正并没有过多分析和研究，因此有必要针对目前传统日变改正方法及应用进行优化，并进行实际数据采集试验验证.

1 地磁组成及地磁静日变化

1.1 地磁组成地磁场T由地球的稳定场T0以及地球的变化场 ΔT两部分组成，其中稳定场是地磁场的主要组成部分，变化磁场 ΔT根据其产生原因又可以分为地球内部 ΔTi和外部 ΔTe两部分，地磁场的表达式：

在磁测过程中，磁力仪采集到的磁场值中变化磁场 ΔT的数值根据其变化类型一般会分成两类.一类是连续并且会持续存在的有一定变化规律的变化磁场如太阳静日变化、太阳月变化，以及年变化等，其中地磁场的长期变化磁场变化周期场，每天变化很小，一般小于0.09 nT，大约为0.07 nT[7]，一般在超过10 d 以上的研究应用中需要关注到该变化；另一类是偶然变化引起的变化磁场，通常这部分磁场经过短暂而复杂的变化后就会消失，没有明显的变化规律，称之为磁扰值或磁异常值.

1.2 地磁静日变化表达太阳静日变化是以一个太阳日即24 h 为周期的磁场变化，太阳静日变化也称之为日变干扰场，是以太阳日为周期的变化场，针对太阳静日变化对地磁场带来的影响以及改正称为日变改正.在实际数据采集过程中常用到的日变改正数学模型为：

式中：(B,L)为观测站的地理坐标；T0(B,L,t)为t时刻的正常磁场；T(B,L,t)为磁力仪观测磁场强度值；T′(B,L)为 日变观测站处的地磁异常值；ΔT(t)为t时刻的日变改变量.如图1 所示为含有一定噪声的一个太阳日的静日变化对地磁场产生的干扰影响曲线图.

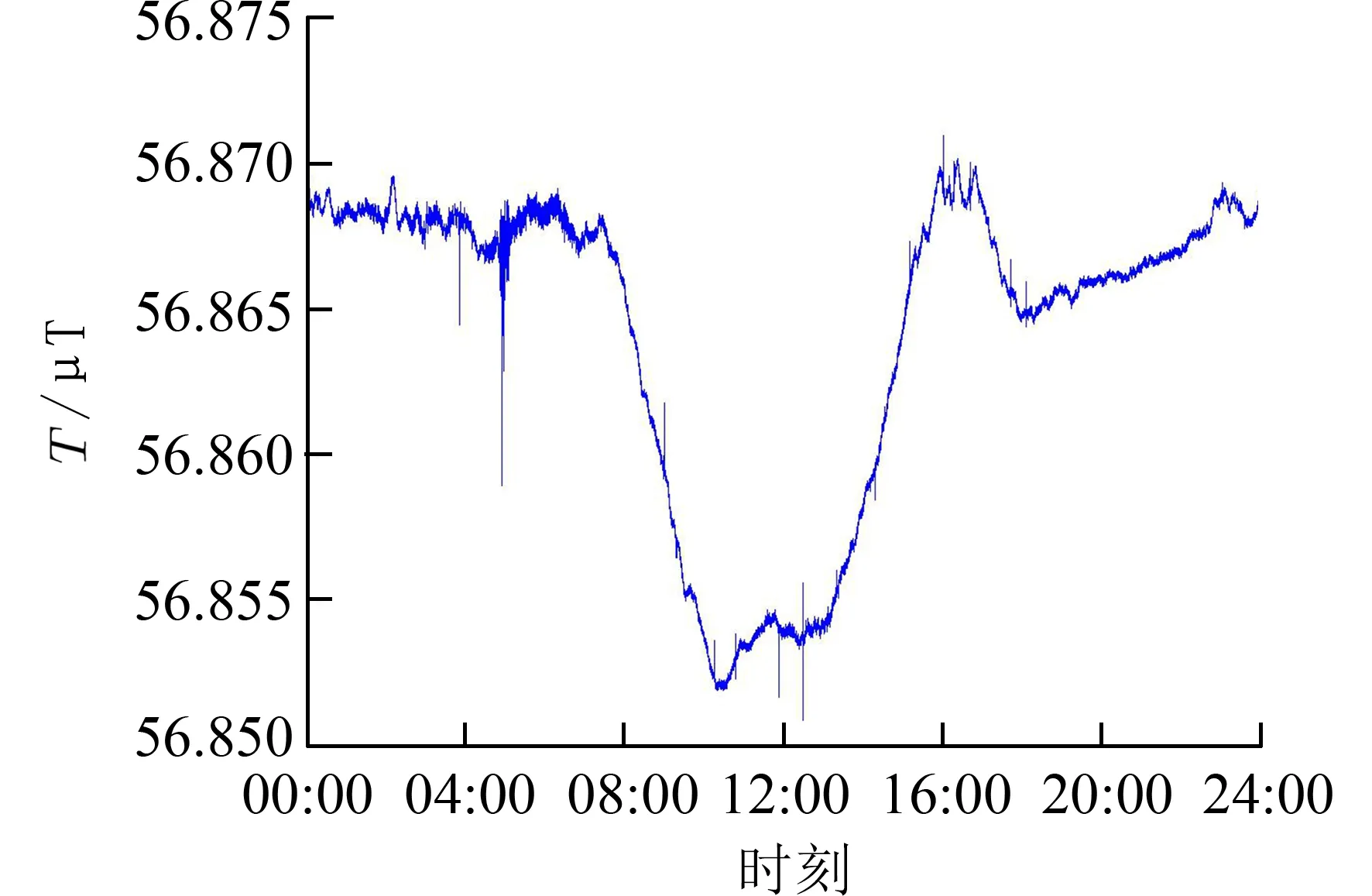
图1 测点原始日变化曲线Fig.1 The curve of the original diurnal variation of the measuring point

由图1 日变化曲线可以发现地磁场的变化在白天变化值较大，夜间的磁场变化趋势很小，整体呈现出类正态分布的变化趋势，变化值差不多也是在几个nT 到几十个nT，同时太阳静日变化的变化值形态在某种意义上更符合高斯函数的变化曲线.

2 数学模型

2.1 传统日变通化校正方法地磁日变通化是通过已知的观测资料获取待测点的地磁日变值，由于地磁台站数量较少，并且稀疏不一，利用地磁日变通化计算可以得到无台站区域的观测资料.地磁日变通化计算易受测点所处的地质环境、地磁指数等因素的影响.地磁数据通化精度直接决定区域模型精度，高精度的区域模型才能提高匹配导航的精度.传统中经常使用的地磁数据日变通化处理方法可以分为多站地磁日变改正和单站地磁日变改正.其中多站地磁日变改正主要包括：直接距离平均法、加权距离平均法和线性内插法、多项式法和函数拟合法等[22]；单站地磁日变改正主要包括基于纬度差和基于距离定权的地磁日变改正方法，以及研究学者最新提出的基于距离、方向以及经纬度中的2 个因子进行加权，最终实现基于双因子加权的地磁日变改正方法[23-24]，在实际数据测量和工程应用中最常见的还是单站地磁日变改正.

2.1.1 直接距离平均法 直接距离平均法是对已知站点的所有观测数据根据台站个数求取观测数据的均值，如式(2)所示，然后利用待求点的实测数据与计算得到的观测均值进行比较分析[22].

式中：Xi为已知站的观测数据，n为台站个数.相关系数的计算采用式(3)计算.

式中：Cov(x,y)=E{[x-E(x)][y-E(y)]}.

2.1.2 加权距离平均法 对站点到待求点之间的距离进行加权求均值，设n个已知台站日变化量为Di(i=1,2,···,n)，站点到待求点的距离为di(i=1,2,···,n)，待求点的日变化量设为M[22]，则加权距离平均法的计算公式：

2.2 高斯函数模型高斯模型通常是用高斯概率密度函数（也称之为正态分布曲线）进行精确地量化事物，把一个事物分解成若干个基于高斯概率密度函数形成的模型，因此高斯分布在一定情况下也被称之为正态分布，是生活中相对常见的一种分布，它的分布函数曲线是1 条上方呈钟形的曲线.

通过采用高斯函数对数据点集进行函数逼近的拟合方法称之为高斯拟合模型，高斯拟合模型在函数拟合过程中具有诸多优点，如拟合速度快、拟合结果准确等.通常情况下，高斯函数对数据点集进行函数逼近后的拟合模型：

式中：Gi(t)为地磁场随太阳静日变化产生的磁场变化值；t为1 个太阳日的时刻，a、b、c分别为拟合模型的参数.

3 试验与分析

试验主要由2 部分组成，单点试验和区域试验：①在一个相对稳定并且没有其他外界干扰的自然环境中选取一个稳定的点位进行多个太阳日连续不间断的数据采集试验，对采集的数据进行拟合分析；②在一定区域范围内设置日变站进行连续日变化的监测拟合，并且实现对周围点位的日变改正.

3.1 单点试验验证对区域场内的单个点位进行5 个太阳日的数据采集，整个采集过程中尽可能保证除去自然变化以外的其他外界环境的干扰影响，如图2 所示为点位连续采集的随太阳日变化的地磁场值的变化趋势图.

图2 点位磁场变化趋势图Fig.2 The variation trend of geomagnetic value of point

由图2 可以看出，除了在R1、R2，即第1 天20:00 以后和第2 天的10:00～20:00 磁测过程中遭受到的剧烈的除日变场以外的外界干扰使得地磁场变化趋势有所异常以外，其他时刻以及其他太阳日的地磁场变化曲线基本符合地磁场的平静日变化规律，即白天波动变化较为剧烈，晚上较为平静.由图2 中曲线可以发现每个连续的太阳日的地磁场变化趋势均呈“凹”字型，去除受影响的波段，对该点位地磁场的变化趋势进行数据处理，以取均值的方式作为每日地磁的基准值，将基准值与整体变化相减，可得到一个“凸”字型的变化趋势，并用高斯函数对地磁场的变化曲线进行拟合，变化值的拟合结果：

式中：a1=-10.9，b1=11.69，c1=8.704，a2=35.97，b2=10.87，c2=2.513，该点位的变化值和拟合值绘制曲线如图3 所示.

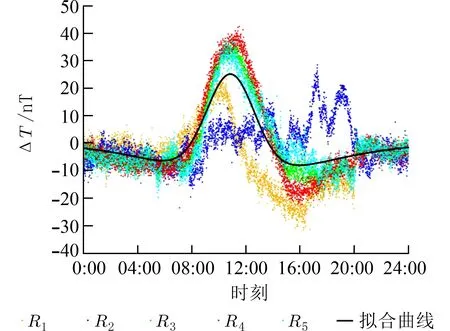
图3 磁场变化拟合值Fig.3 Fitting curve of geomagnetic variation

对比拟合结果进行量化分析，将点位的磁场变化量与拟合结果进行对比分析，如表1 所示为点位部分时刻比对结果，由表1 对比结果可得，该点位的拟合结果相对较好，除个别受到其他外界干扰情况的时刻，拟合误差都在几个nT 以内，中误差也不超过10 nT.拟合结果在一定程度上能够表达点位的日变化情况，可以在此基础上考虑对区域点位进行日变改正试验.

表1 拟合对比结果Tab.1 Comparison of fitting results nT

3.2 区域试验验证

3.2.1 数据介绍 选取国内北部相对空旷的草原区域进行区域日变改正试验研究，该区域周围无合适的地磁台站作为日变站进行数据采集，因此需要设置虚拟日变站进行地磁数据采集和日变改正.在区域中心点的位置设置日变站并对该点位的地磁数据进行相对连续的数据采集，因点位地处空旷的草原，周围基本上不存在其他外界电磁波干扰，整体环境相对稳定.将磁力仪按照规定要求进行安置后开机进行不间断的数据采集工作，以此中心点点位日变站为基准对区域范围内的地磁场信息进行数据采集和改正，数据采集示意图如图4 所示.

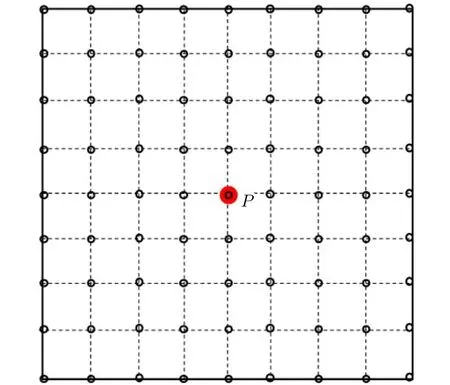
图4 试验点位安排示意图Fig.4 Schematic diagram of arrangement of test points

图4 中中心红色点位P为日变站设立的位置，P在区域中心位置，将该区域等分为大小相等的25 m×25 m 格网进行数据采集工作，每个点位都将进行连续多次测量以保证其数据精度，对采集的区域点位地磁数据通过日变改正，最后得到该区域的地磁场信息.

3.2.2 基于高斯函数的日变规律分析 对设立的日变站P进行连续不间断的地磁数据采集后，观察其变化规律为夜间变化较小相对平稳，白天在一定时间范围内变化相对较大.但实际区域数据采集工作的人员作业时间有限，基本均为白天工作，在后期数据采集工作中采取只在作业时间范围内进行日变站同步数据的采集工作，整体的野外数据采集的采样间隔设置为3 s.如表2 所示为P点一个太阳日连续采集的部分数据，图1 为该点位一个太阳日的连续监测变化曲线.

表2 P 点不同时刻磁场值部分数据Tab.2 Geomagnetic value at different times of point P

区域地磁数据采集工作进行时，对该日变站进行同步连续监测，采集工作在白天进行，如图5 所示为日变站在不同太阳日的工作时刻即09:00～16:00 的地磁场日变化趋势曲线及其变化值曲线.

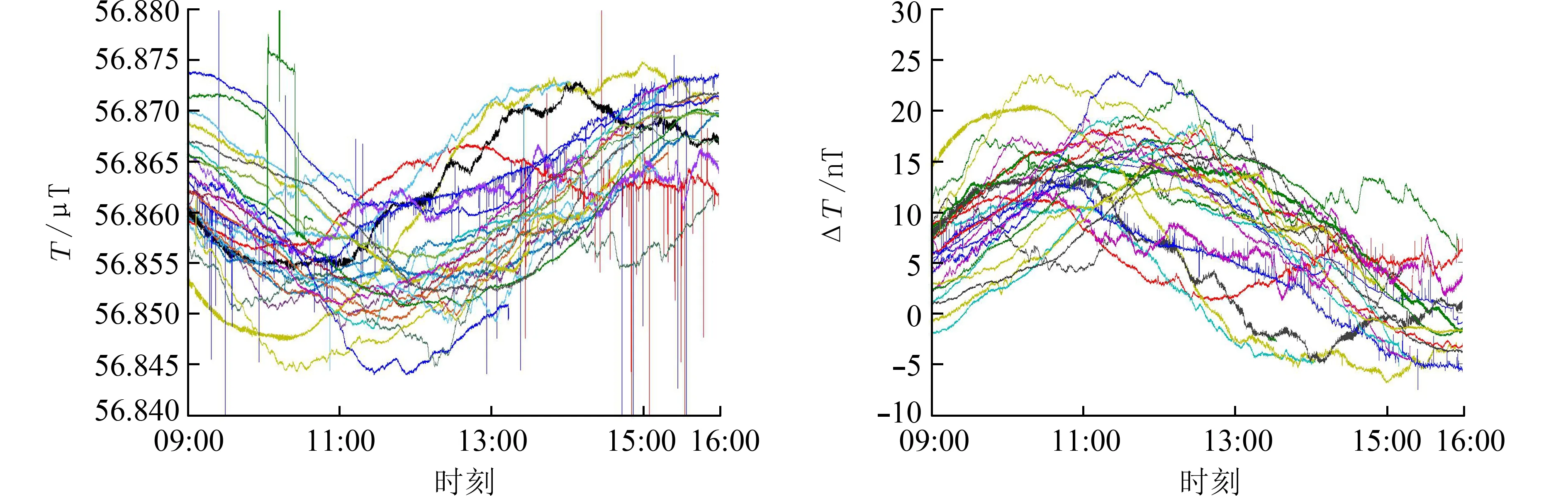
图5 日变监测站观测值及其变化值Fig.5 Observation value and variation value of diurnal variation monitoring station

将日变站P的一个连续太阳日内获取的磁原始数据（图1）进行去基值，然后绘制该点位的变化值曲线如图6 所示.

图6 点位磁场变化图Fig.6 Variation diagram of geomagnetic

由图1 的原始变化和图6 的点位磁场变化曲线均可以看出该日变站数据监测过程中存在一定的噪声影响，在某些时刻还会存在一些较大的突变，针对这些噪声在剔除粗差的基础上选用平滑函数对剩余较小噪声进行平滑去噪处理.对该站数据进行去基值处理的过程中选用均值法作为基值.整个试验过程日变站监测连续不间断工作，将日变数据根据高斯函数进行拟合：

式中：a=16.3,b=11.53,c=2.93，其日变化值拟合曲线如图7 所示.

图7 日变监测站拟合结果Fig.7 Fitting results of diurnal variation monitoring station

3.2.3 精度评估 选用高斯函数拟合的日变站估值对区域地磁场数据进行日变改正，类比采用多站观测精度对比分析的方法将高斯拟合获得的日变改正结果与常规日变改正结果进行对比分析，得到的结果如表3 所示.

表3 部分点位日变改正对比Tab.3 Comparison of diurnal variation correction of some points nT

点位的日变改正结果的差值的频率表如表4所示，可看出高斯拟合估值获得的日变改正结果与传统的日变改正结果的差值大都在±10 nT 以内，82.3%的点位差值在±5 nT 以内，改正结果相当，说明拟合函数获得的日变改正精度一定程度上可以满足地磁数据采集的日变改正需求.

表4 相对误差频数频率表Tab.4 Frequency of relative error

由表3 和表4 的对比结果可以发现高斯函数拟合得到的日变改正结果与常规方法获得的日变改正值相差不大.该拟合函数的特点在于通过构建函数模型在已知区域点位地磁数据的观测时间获得该区域的一个日变改正值，为提高日变改正工作效率提供了可能.

4 结论

（1）单点位日变改正拟合试验中，通过对比单点位5 个太阳日的地磁数据与高斯拟合结果做对比，结果发现在正常太阳日变化情况下，拟合误差较小，基本上都在几个nT 以内，中误差也都不超过10 nT，说明高斯函数拟合的地磁场日变化的拟合结果基本上可以满足日变改正的需求.

（2）区域范围内日变改正的对比试验中，根据不同点位相对日变站拟合的日变改正值进行改正，该方法与常规日变改正方法得到的日变改正值的差基本上都在±10 nT 以内，82.3%的点位日变改正差在±5 nT 以内，说明该函数拟合方法获得的日变改正精度一定程度上可以与常规改正方法相媲美，可以满足地磁数据采集的日变改正需求.

将高斯函数应用在地磁日变改正的研究中为常规地磁日变改正提供了新的思路，整个试验结果表明，拟合函数获得的日变改正结果在一定区域内精度与常用的日变改正方法的改正精度相当；通过构建拟合函数模型在已知区域点位地磁数据的观测时间快速获得该区域的1 个日变改正值，有望提高工作效率；为区域地磁日变改正实际应用以及无台站或日变站无法持续工作等情况下的地磁日变改正问题提供了方法和思路，可以一定程度上提高区域地磁场建模的前期数据处理效率，有一定的研究意义.