基于前馈补偿LQR 与PID 的矿井无轨胶轮车横纵向控制研究

江 松 武露云 付信凯 顾清华 洪 勇 章 赛 卢才武

(1.西安建筑科技大学资源工程学院,陕西 西安 710055;2.中钢集团马鞍山矿山研究总院股份有限公司,安徽 马鞍山 243000;3.金属矿山安全与健康国家重点实验室,安徽 马鞍山 243000;4.中钢集团山东富全矿业有限公司,山东 济宁 272000)

随着智慧矿山理念的提出,矿山智能化[1]和无人化建设[2]正在不断推进。 无轨胶轮车[3]作为井工矿重要的辅助运输设备,主要用于井下设备和人员的运输[4],因其爬坡能力强、载重能力大、运输成本低等优点被广泛应用。 井下工作环境恶劣,巷道工况复杂、岔路口和视野盲区较多、突发危险情况较多,人为驾驶极易引发安全事故。 因此,研究井下无轨胶轮车的无人驾驶技术[5],有利于减少井下人工运输事故和经济损失,降低人工运输成本,提高采矿工作效率。轨迹跟踪作为无人驾驶技术中尤为重要的一环,其跟踪控制的精度决定了车辆行驶的安全性。 因此,解决井下无轨胶轮车的轨迹跟踪问题[6]对于推动矿山无人化[7]建设具有重要意义。

针对轨迹跟踪问题,国内外学者已经提出了很多处理方法,目前主流的轨迹跟踪控制方法有模型预测控制[8]、比例积分微分控制[9]、模糊控制[10]、线性二次最优控制[11]、滑模控制[12]。 赵红专等[13]以车辆运动学的MPC 理论为依据,引入车辆动态间距理念,提出了一种适用于弯道驾驶的跟踪模型,提高了弯道工况下车与车之间的安全性、可靠性和驾驶者舒适度。方培俊等[14]提出了一种基于机理分析—数据驱动的车辆动力学串联混合模型,进而设计了符合实际行驶环境的轨迹跟踪控制方案。 LIN 等[15]采用线性3 自由度车辆动力学模型作为预测模型,提出了一种模型预测控制与模糊比例积分微分控制相结合的综合控制方法。 CHEN 等[16]引入了前向—后向积分方案以生成受轮胎—道路摩擦限制的时间最优速度分布,改进后的MPC 控制器对轨迹和速度的跟踪性能良好。CHENG 等[17]考虑随时间变化的车辆速度,利用具有有限顶点的多面体描述车辆纵向速度,建立了线性参数变化的横向模型,设计了基于MPC 的车辆路径跟踪控制器。 YU 等[18]利用智能聚类算法AGA、QPSO和ACA 对LQR 参数优化,实现了井下铰接铲运机的无人驾驶路径跟踪控制。 王宏伟等[19]针对无人车在复杂行驶工况下,非线性约束条件增多导致的算法复杂度升高、系统求解速度降低的问题,通过引入连续增加的惩罚系数,提高了模型预测控制算法的求解效率。 马浩楠等[20]针对井下无人车在狭窄巷道轨迹跟踪难度大的问题,提出了一种基于空间偏差的模型预测算法(SMPC),通过降低预测方程维度,在一定程度上解决了控制器求解效率低的问题。

上述无人驾驶技术在城市道路场景中已经逐渐成熟,但对于工况复杂巷道狭窄的矿山井下运输场景,目前还未形成成熟的理论与技术体系。 车辆在运行过程中的速度[21]与轨迹是随时间变化而变化的,现阶段有关井下无轨胶轮车轨迹跟踪控制的研究只考虑了轨迹变化对控制的影响,很少同时考虑速度变化[22]因素。 由于不同矿区井下工况的特殊性和差异性,如果不对井下场景做细分化处理,跟踪控制方案可能面临场景不适配等问题[23]。

为此,本研究设计了基于5 次多项式曲线的井下无轨胶轮车换道轨迹模型,来解决轨迹跟踪过程中轨迹与速度的时变问题,并对井下不同行驶工况进行分类,验证不同工况下横纵向协调控制器的稳定性和鲁棒性。

1 考虑轮胎侧偏的车辆模型

1.1 Pacejka 经验轮胎模型

车辆在行驶过程中,轮胎受到侧向力、纵向力、垂向力等的作用,对车辆行驶过程中的稳定性和安全性有着重要影响。 由此可见,在建立井下车辆动力学模型过程中有必要充分考虑轮胎特性对其运动控制的影响。

为了使本研究试验更加符合实际情况,以无轨胶轮车的轮胎性能参数为例,通过Pacejka 提出的魔术公式半经验轮胎模型,建立轮胎侧向力与侧偏角之间的关系,从而计算出轮胎的侧偏刚度。 魔术公式的一般表达式为

式中,A0为刚度因子;B0为形状因子;C0为峰值因子;D0为曲率因子。

轮胎垂向载荷为10 000 N 时,轮胎侧偏力与轮胎侧偏角的拟合曲线如图1 所示。A0、B0、C0取值可由拟合结果得到。

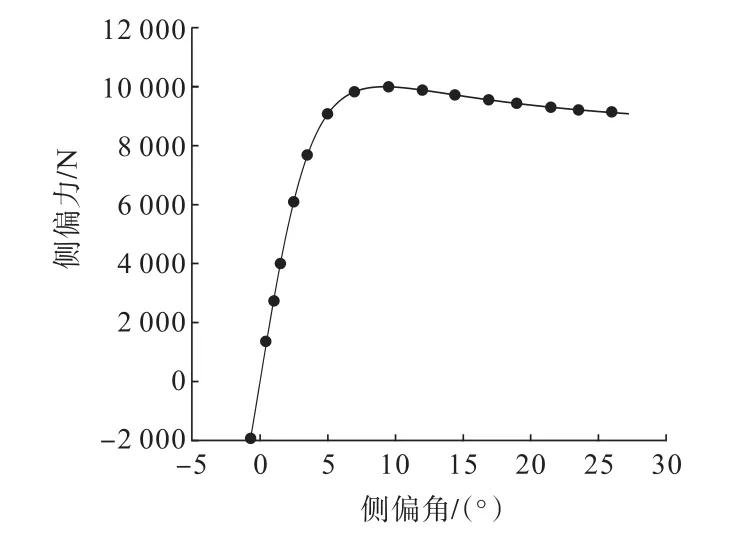
图1 轮胎侧偏刚度拟合曲线Fig.1 Fitting curve of tire lateral deflection stiffness

当轮胎侧偏角较小时,轮胎侧向力可以近似表示为轮胎侧偏角的线性函数,此时曲线斜率即为轮胎的侧偏刚度。

1.2 车辆动力学模型

由于本研究在Frenet 坐标系下实现了车辆横纵向运动解耦控制,因此在建立车辆自由度模型时只需考虑横向运动和横摆运动2 个自由度,忽略纵向运动的影响。 由于井下运输场景为低速小转角场景,因此,其操纵特性可用线性2 自由度“自行车”模型来近似描述。 简化后的动力学模型简单稳定,计算复杂度大幅减少,且能较好地适应井下极限复杂工况。 本研究采用线性2 自由度模型作为前轮转向无轨胶轮车动力学模型,如图2 所示,其中XOY坐标系为大地坐标系,xoy坐标系为车身坐标系。

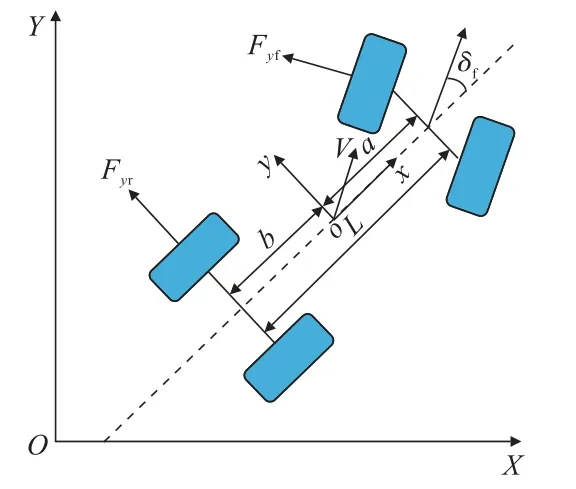
图2 无轨胶轮车二自由度动力学模型Fig.2 Trackless tyred vehicle two-degree-of-freedom dynamics model

考虑轮胎侧偏特性,对车辆进行受力分析,根据其受力平衡和力矩平衡可以得到:

式中,m为整车质量,kg;ay为车身坐标系下y方向加速度分量,m/ s2;为航向角导数;I为转动惯量,kg·m2;对δf做小角度假设,则cosδf=1。

结合前后轮侧偏角和侧偏刚度可以得到无轨胶轮车动力学模型,本研究进一步将其转化为矩阵形式可得:

式中,νx为车辆纵向速度,m/s;Cαf、Cαr为前后轮侧偏刚度,N/rad;αf、αr为前后轮侧偏角,rad。 该式即为横向运动控制方程,通过控制δf,控制和,进而控制横向位移y和航向角φ。 该模型能很好地反应车辆的横摆特性,不足在于未能考虑车辆的侧倾动力学特性。 但是由于井下运输场景为低速场景,因而可以近似忽略侧倾因素对车辆横向控制的影响,简化后的模型精度仍能得到保证。

1.3 跟踪误差模型

由于简化后的模型不考虑车辆的侧倾特性,只考虑横向和横摆运动,因此只需考虑横向误差和航向误差。 本研究横向误差定义为车辆后轴中心与其在道路中心线上投影点之间的距离偏差,航向误差定义为车辆航向与道路方向的偏差。 误差模型如图3 所示。

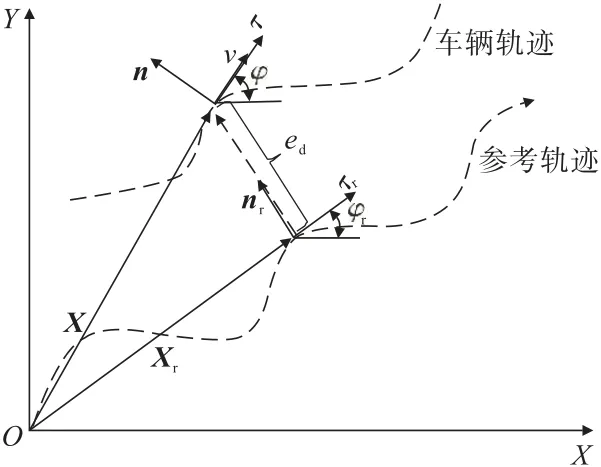
图3 轨迹跟踪误差模型Fig.3 Trajectory tracking error model

误差参数可以表示为

式中,νy为车辆横向速度,m/s;为横向误差导数;为航向误差导数;为参考轨迹航向角导数。 将式(5)代入式(4),化简可得误差矩阵

式中,A、B、C为参数系数矩阵和向量;err为误差参数向量;为误差参数矩阵的导数向量。

2 横纵向控制器设计

井下巷道如图4 所示,井下车辆的工作环境恶劣、工况复杂,场景受到巷道宽度[24]限制,单一的横向或纵向控制难以应对井下突发情况。 横纵向协同控制才是实现井下无轨胶轮车无人驾驶的关键。

图4 井下巷道Fig.4 Underground roadway

2.1 轨迹规划设计

本研究选择5 次多项式法规划无轨胶轮车的换道轨迹,基于5 次多项式曲线拟合出的车辆行驶轨迹曲率连续平滑无突变,而且保证了速度、位移和加速度连续,使得控制更加稳定。

采用5 次多项式曲线规划的轨迹,其横坐标x是关于时间t的5 次多项式,纵坐标y是关于x的5 次多项式拟合结果,规划过程中需要对轨迹的曲率、速度和加速度进行限制。 基于5 次多项式规划的轨迹可表示为

式中,a0～a5、b0～b5为多项式系数。

规划后的横向误差和纵向误差可以表示为

式中,xr为规划轨迹横坐标;yr为规划轨迹纵坐标。

2.2 横向LQR 控制器设计

线性二次型最优控制是稳定的轨迹跟踪横向控制方法,可利用较少的计算成本使系统达到较好的性能指标,也可以构成闭环最优控制。 因此,本研究采用离散空间LQR 控制设计横向轨迹跟踪器。 LQR 控制方法的本质就是求解满足约束xk+1=A·xk+B·uk的性能函数J取得最小值时的最优控制量uk。 则有:

式中,xk为自变量矩阵;Q为半正定的状态加权矩阵;R为正定的控制加权矩阵,两者通常为对角矩阵;矩阵Q元素变大意味着状态量能够快速趋近于0;矩阵R元素变大意味着希望控制输入能够尽可能小,系统的状态衰减将变慢;Q、R取值需根据具体的实际应用场景而定。

经过仿真调试验证,最终Q、R取值为

本研究利用拉格朗日乘子法,迭代求解得到Riccati 方程的解P。P满足

令反馈系数矩阵K=-(R+BT·P·B)-1·BT·P·A,最终得到优化的控制量

在线求解Riccatti 方程会增加系统的计算复杂度,降低系统的响应速度。 因此,本研究通过离线计算得到不同车速vx对应的反馈矩阵K,进而得到不同车速下的反馈系数,使用离线LQR 的控制系统实时性大大增强。

2.3 前馈补偿控制器设计

由式(7)和式(13)结合误差反馈可得

由式(14)可知,若只使用LQR 控制算法,不论反馈系数K取何值,和err不可能同时为0,说明系统此时存在不可消除的稳态误差。 因此,为了消除系统稳态误差对横向控制结果的影响,本研究通过前馈控制引入前轮偏转角δf,待系统稳定后,,此时

因此只需选取合适的δf,使得上式尽可能为0,即可消除系统的稳态误差。 对上式化简后可得到

式中,k为曲率;K3为反馈系数矩阵第3 项。

井下运输车辆由于其自身转向不足的特性,即车辆需要更大的转向角度来保持行进路线,在应对复杂的行驶工况时,会增大实际轨迹与规划轨迹之间的横向误差。 为了消除车辆自身特性导致的不利因素,减小横向稳态误差,本研究提出了前馈补偿控制策略,使用PID 的积分模块对输出的横向误差ed进行积分处理,将积分后的结果补偿给前轮偏转角。 当道路曲率过大时,车辆会因转向不足导致方向盘转角过小,此时需要前轮偏转角加上补偿量Δδf(式(17)),得到最终的方向盘转角。 通过对改进前后横向误差结果对比可知,轨迹跟踪的精度显著提高。

式中,ki为积分项系数。

2.4 纵向PID 控制器设计

纵向控制采用了双PID 控制器设计,速度PID控制器主要用于车辆车速的控制,通过调节比例项与积分项来减小规划速度与实际速度之间的误差值ev,位置PID 控制器主要负责控制车辆实际位置与规划位置之间的纵向位置误差es。 通过调节比例项提高系统的响应速度,但比例项kp过大会增加稳态误差引起超调;调节微分项kd减小超调量,提升控制的稳定性。 最终使得系统满足精度和稳定性要求的系数分别为kp=3、ki=0、kd=0.1。

为了实现纵向控制器对纵向位置误差和速度误差的精确控制,还需要得到车辆准确的驱动制动参数。 因此,本研究依据某矿山井下运输车的电机参数,建立电机仿真模型,通过试验得到车辆在加速减速过程中的油门和刹车开度值。 电机最大功率Pmax为40 kW,最大扭矩Mmax为160 N·m,通过计算可得到电机恒扭矩与恒功率输出的电机转速的临界值ωc为2 388 r/m。 因此,转速和扭矩关系可以表示为

式中,ω为电机转速,r/m;thr为油门踏板开度。

利用该模型,并根据车辆在行使过程中的速度和加速度可以实时输出车辆的油门踏板开度和刹车踏板开度,从而得到4 个物理量的关系,进一步可以拟合得到三维曲面关系,如图5 所示。

图5 油门刹车开度三维曲面Fig.5 Three-dimensional surface of the throttle brake opening

3 仿真与分析

本研究使用5 次多项式曲线建立参考轨迹模型,以横向控制器、前馈补偿控制器和纵向速度控制器作为核心控制器,通过Carsim 与Matlab/simulink 联合仿真,分别在井下双车道、单车道与颠簸路面场景下进行轨迹跟踪控制算法验证。

3.1 车辆仿真参数设置

本研究以Carsim 中重型皮卡车型为模拟车型,并以某矿山的井下无轨胶轮车实车参数为标准,修改相关模拟参数,建立更加符合工程实际的车辆仿真模型,具体仿真参数取值见表1。

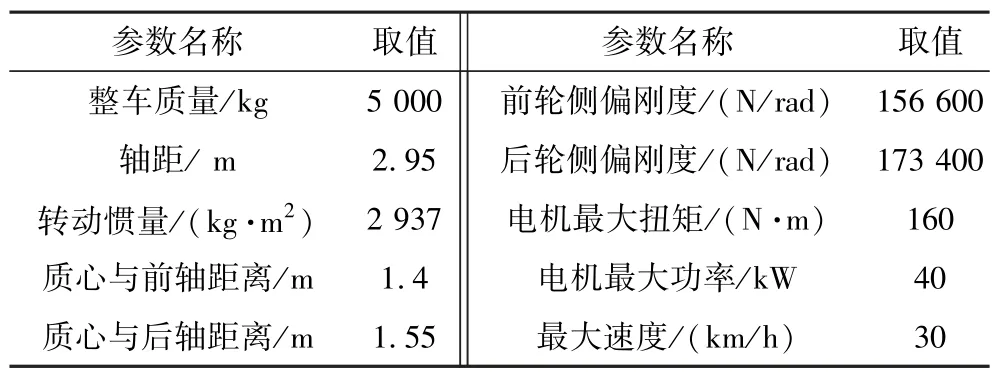
表1 井下无轨胶轮车动力学仿真参数Table 1 Basic parameters of underground transport vehicle dynamics

3.2 仿真工况模拟

本研究通过实地考察,根据某矿山井下巷道宽度设计标准和车辆运行速度标准,设计了井下双车道避障换道工况、单车道会车工况与颠簸路面工况,测试所设计控制器的精确性和鲁棒性。 通过分析在不同工况下车辆的横向误差和纵向误差验证轨迹跟踪的效果和精度,以及分析速度误差、转向角变化评价车辆运行过程中的稳定性和舒适性。

工况1:井下双车道超车或避障场景如图6 所示。 其中黑色代表矿井巷道墙壁,巷道宽度为5. 3 m,设置车辆初速度为28.8 km/h,末速度为18 km/h,加速度为-2 m/s2;红色表示车辆的规划行驶路线,对应的真实场景为车辆先减速驶入变道车道再加速超过前车或避开前方障碍物,车辆行驶过程中车速小于30 km/h,符合井下运输车辆速度标准。

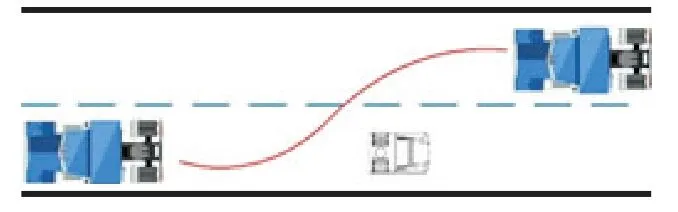
图6 双车道避障工况Fig.6 Two-lane obstacle avoidance condition

工况2:井下单车道会车场景道路工况如图7 所示。 由于单车道巷道狭窄,因此,运输过程中车辆需要借助躲避硐室进行会车。 为验证控制器在该场景下的可靠性,以5 次多项式模拟车辆的行驶路线,第一段曲线车辆的初速度为18 km/h,末速度为0,加速度为-1 m/s2,第二段曲线车辆初速度为0,末速度为18 km/h,加速度为2 m/s2,2 段曲线共同构成车辆的轨迹。 对应的真实场景为车辆先减速驶入躲避硐室停车,完成会车后再加速驶出。

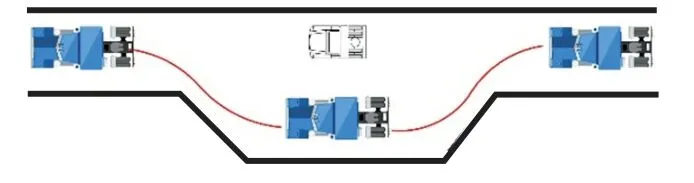
图7 单车道会车工况Fig.7 Single-lane meeting condition

工况3:井下颠簸路面场景。 车辆在颠簸路面行驶过程中,轮胎在纵向和侧向的载荷会发生改变,前轮垂向载荷增大,轮胎的侧偏刚度增大,会对车辆轨迹跟踪的控制效果产生影响。 本研究在建立车辆动力学模型时,考虑到车辆轮胎的侧偏特性,通过改变轮胎的侧偏刚度,模拟车辆在颠簸路面下的行驶状态,进一步验证该控制器在颠簸路面场景下的稳定性。颠簸路面下的车辆前轮侧偏刚度为185 000 N/rad,后轮侧偏刚度为205 000 N/rad。

3.3 仿真试验与结果分析

由于井下行驶工况特殊,车辆运行速度小于30 km/h,因此仿真工况均为低速工况,3 种仿真工况下,车辆规划轨迹与实际轨迹的误差对比如图8 所示。由图8 可知:3 种工况下横向控制误差均小于5 cm,因此证明该控制器在井下具有较高的跟踪精度。

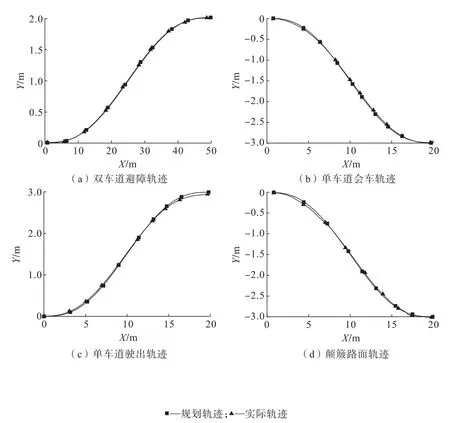
图8 3 种工况规划轨迹与实际轨迹对比Fig.8 Comparison of planned trajectory and actual trajectory for three working conditions

双车道工况下本研究对横纵向控制器改进之后的仿真结果如图9 所示。 由图9 可知:速度PID 控制器对当前车速有很好的控制效果,但是会引起一定的超调,在7.8 s 处速度误差最大为0.2 m/s。 图9(c)为对位置PID 控制器调参前后控制效果对比。 分析可知:通过位置PID 对纵向控制改进之后,纵向位移误差减小幅度明显,最大减幅为10 cm。

图9 双车道工况改进前后仿真结果对比Fig.9 Comparison of simulation results before and after the improvement of the two-lane working condition

单车道会车工况下,改进前后横向误差与速度误差对比分析结果如图10 所示。 通过分析在减速和加速过程中的横向误差曲线,可知在减速路段误差控制在8 cm 以内,加速路段误差在10 cm 以内。 本研究使用改进后的横向控制器后,减速路段横向误差减小到2 cm 以内,加速路段误差减小到5 cm 以内。 由于井下单车道道路狭窄工况苛刻,因此LQR 横向控制器误差较大,前馈补偿改进后的横向最大误差减少幅度在50%以上。 图10(c)和图10(d)为单车道减速路段和加速路段下实际速度与规划速度的对比结果。通过对比分析可知:在车辆加速阶段速度误差较大,最大误差出现在路段二3.2 s 处,此时速度误差最大约为1 m/s。

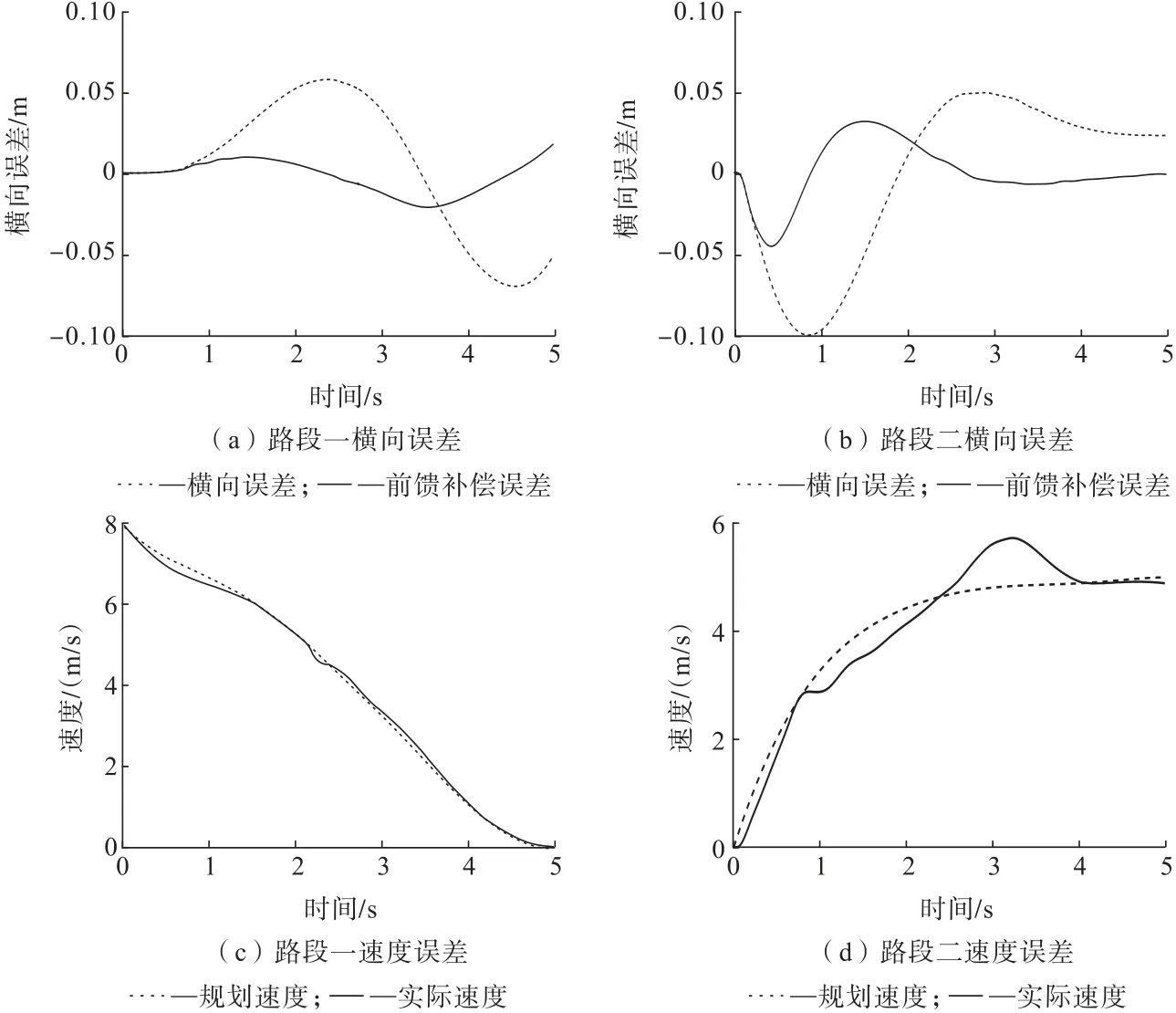
图10 单车道改进前后横向误差与速度误差对比Fig.10 Comparison of lateral error and speed error before and after single-lane improvement

为验证控制器在井下工况下的稳定性和鲁棒性,本研究分析了车辆在轨迹跟踪过程中前轮偏转角和航向误差参数,结果如图11 所示。 由图11 可知:在低速工况下车辆的前轮偏转角变化平缓无明显突变,航向误差控制在±0.1 rad 以内,表明所提出的轨迹跟踪控制方法在井下工况中也能保证车辆转向的舒适性和稳定性。

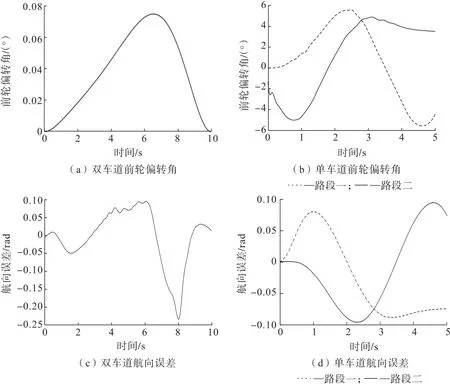
图11 前轮转角与航向误差变化Fig.11 Change of front wheel angle and course error

3.4 井下实际巷道场景试验

为验证本研究构建的控制器在井下实际场景下的控制效果,通过使用实验室小车于陕西某矿山井下进行了现场试验。 该小车底盘为阿克曼转向结构,搭载传感器为速腾16 线激光雷达,采样频率为10 Hz;HIPNUC 的9 轴IMU,采样频率为400 Hz,机载计算机为Intel(R) Core(TM) i7-11390H CPU,16GBRAM,512G 固态,编译语言为C++,ROS 版本为Noetic,系统为Ubuntu 20. 04,小车使用激光SLAM 实现井下定位,定位误差为厘米级。 车辆在3 种工况下多次运行的试验结果见表2。 井下巷道2D 地图如图12 所示,井下现场试验场景如图13 所示。 通过对控制器多次轨迹跟踪的误差数据进行对比分析得出,3 种工况下横向最大误差为6.6 cm,纵向最大误差为56 cm,速度最大误差为0.5 m/s。 试验结果表明:井下颠簸路面的确会对轨迹跟踪误差产生影响,但其误差也在合理范围内,因此,改进后的控制器在井下场景具有较好的应用效果。

表2 3 种工况下最大跟踪误差结果Table 2 Maximum tracking error results under 3 working conditions

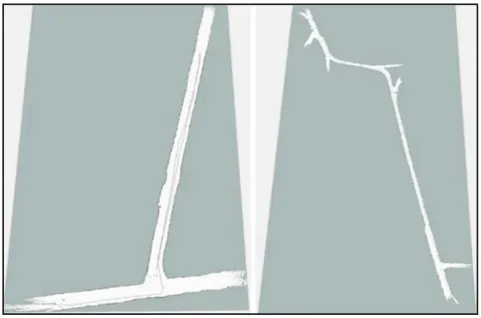
图12 井下巷道2D 地图Fig.12 2D map of underground roadway

图13 井下颠簸路段与躲避硐室Fig.13 Underground bumpy road and escape chamber

4 结 论

(1)提出了基于PID 积分项前馈补偿的横向控制器,优化了车辆输出的前轮偏转角,减小了横向控制误差,解决了因前轮偏转角突变引起的方向盘抖动问题,改进后的横向LQR 控制器转向稳定,更能适应井下巷道工况。

(2)构建了井下实车参数电机模型,通过试验标定得到油门、刹车与速度、加速度的变化关系,并利用PID 控制器调整车辆的位置误差和速度误差,同时解决了车辆运行过程中的速度和路径的时变问题。

(3)通过Carsim 和Simulink 分别对井下双车道、单车道和颠簸路面工况进行仿真分析,并在井下实际环境中进行了试验验证。 结果表明:该控制器能够将跟踪误差控制在较小范围内,具有较高的控制精度和稳定性。 但试验中并未考虑车体质量变化对跟踪控制的影响,因此,建立更为精确的模型实现井下全局纵横向耦合控制是下一步研究方向。