非圆弧拱面内自由振动实用解析

胡常福, 朱顺顺, 张 鑫, 罗文俊

(华东交通大学 土木建筑学院,南昌 330013)

拱结构的自由振动特性,是反映其结构健康状态的重要指标,一直是学者和工程师关注的重点。采用极坐标系表达的圆弧拱结构自由振动问题,已经得到了大量研究者的关注[1-2]。然而,圆弧拱对应着以等深静水压力为代表的均匀径向荷载,在竖向荷载为主的拱桥工程中应用较少[3-4]。拱桥工程中的拱轴线与荷载,均以笛卡尔直角坐标系为基础。因此,研究笛卡尔直角坐标系下非圆弧拱结构自由振动问题,在拱桥工程中有着重要的意义。

针对笛卡尔直角坐标系下非圆弧拱结构的自由振动问题,Lee等[5]在直角坐标系下通过数值方法计算了固接、铰接的抛物线拱的自由振动振型与频率;Yau[6]研究了抛物线两铰拱在移动荷载与竖向地面激励共同作用下的振动问题;Serdoun等[7]基于有限元法和高阶剪切变形理论研究了抛物线复合材料拱固有频率的影响因素;Eroglu等[8]采用无量纲方法,通过矩阵求解拱结构控制方程,得到抛物线拱固有频率变化与损伤位置的关系;刘茂等[9]基于绝对节点坐标法研究了变截面Euler-Bernoulli拱的面外振动特性。

以上笛卡尔直角坐标系下拱结构自由振动的研究中,均使用数值方法,未能得到非圆弧拱结构自由振动解析。解析解或实用解析对揭示力学现象、促进行业规范更新等方面有着重要的意义。为填补非圆弧拱结构面内自由振动解析的空白,本文以笛卡尔直角坐标系下拱结构线性应变与Hamilton原理为基础,推演非圆弧拱结构面内自由振动变系数平衡微分方程;基于陡拱与浅拱振型的相似性,推演得到非圆弧拱面内自振频率高精度实用解析,揭示了非圆弧拱自振频率与同参数直梁非一阶面内自振频率之间的比例关系,并通过有限元数值结果验证了本文方法的精确性。

1 非圆弧拱面内自由振动变系数平衡微分方程

1.1 基本假定与坐标系

为推演笛卡尔直角坐标系下非圆弧拱结构面内自由振动实用解析,使用以下基本假定:

(1) 拱结构面内自由振动是线性小挠度的,不考虑拱结构的几何非线性效应;

(2) 结构自由振动过程中,材料始终处于弹性工作范围内;

(3) 结构所有面外位移均被约束;

(4) 结构以竖向振动为主,水平振幅远比竖向振幅小;

(5) 结构面内自由振动是微小的,不会引起拱结构轴线长度的变化;

(6) 结构面内自由振动为简谐振动,陡拱与浅拱振型没有显著差异。

如图1所示,本文使用2个笛卡尔直角坐标系,全局坐标系yoz与局部坐标系y*o*z*来描述非圆弧拱面内自由振动。全局坐标系yoz的原点o位于左侧拱脚处,oz轴水平向右,oy轴竖直向下;局部坐标系y*o*z*的原点o*是拱轴线上任意一点,o*z*为o*点拱轴线的切线方向,y*o*是o*点拱轴线的内法线方向。

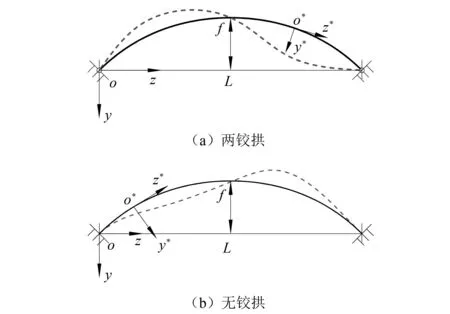
图1 非圆弧拱面内自由振动

1.2 变系数平衡微分方程

根据基本假定式(1)与式(2),非圆弧拱结构面内线性自由振动满足Hamilton基本原理[10-12]:系统微小的虚位移引起的虚动能与虚势能的和为零,可表示为

(1)

式中:T与U为非圆弧拱结构动能与势能;δ(·)为变分函数;t为时间,t1与t2为任意2个时刻。直角坐标系下非圆弧拱结构面内自由振动时的虚动能,可表示为

(2)

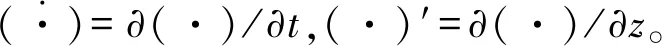
(3)

式中:V为拱结构体积;εm与εb为拱结构面内压缩与弯曲应变;σm与σb为拱结构面内压缩与弯曲应力,σm=Eεm,σb=Eεb,E为拱结构弹性模量,在笛卡尔直角坐标系下非圆弧拱面内线性应变可表示为[13-14]

(4)

式中:y*为非圆弧拱主拱圈横截面内法线坐标;y为非圆弧拱轴竖坐标;z为全局笛卡尔直角坐标系横坐标;f为拱结构矢高;(·)″=∂2(·)/∂z2。将式(4)代入式(3),可得非圆弧拱结构自由振动时虚势能为

(5)

将式(2)与式(5)代入式(1),并考虑虚位移δw与δv的任意性,可得非圆弧拱面内自由振动水平方向平衡微分方程

(6)

与竖直方向振动平衡微分方程

(7)

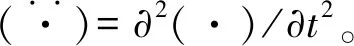
(8)

根据欧拉伯努利梁理论可知,拱轴力N可表示为

N=-EAεm

(9)

根据基本假定式(5)可知,非圆弧拱结构在面内小幅自由振动,不会引起拱轴线长度的变化,可得

(10)

将式(10)代入式(7),可得

(11)

式(11)即为笛卡尔直角坐标系下非圆弧拱结构面内自由振动变系数平衡微分方程。

2 非圆弧拱自由振动变系数平衡微分方程实用解析

由于数学学科中变系数微分方程研究不够成熟,如式(11)所示的非圆弧拱结构面内自由振动变系数微分方程无法得到解析。因此,必须对如式(11)所示的变系数微分方程进行适当简化与近似,方能获得高精度实用解析,以期在拱桥规范修订中发挥应有的价值。

如式(11)所示的非圆弧拱结构面内自由振动变系数平衡微分方程,当满足浅拱假设时[15]

1+y′2≈1

(12)

式(11)可以简化为非圆弧浅拱面内自由振动的常系数平衡微分方程

(13)

式中:v0为非圆弧浅拱竖向自由振动位移;(·)iv=∂4(·)/∂z4。如式(13)所示的常系数微分方程通解为

v0(z,t)=v0(z)sin(ω0t)

(14)

式中:ω0为非圆弧浅拱自振频率;v0(z)为非圆弧浅拱振型,可以表达为

(15)

式中: sh(·)为双曲正弦函数;ch(·)为双曲余弦函数;c1,c2,c3,c4为任意常数。根据非圆弧陡拱与浅拱在面内振型上没有显著差异基本假定可知,如式(11)所示的陡拱面内变系数平衡微分方程的解与如式(13)所示的浅拱面内常系数平衡微分方程的解,具有相似性。因此,式(11)解的形式可以近似表示为

v(z,t)=v(z)sin(ωt)≈v0(z)sin(ωt)

(16)

式中:v(z)为非圆弧陡拱结构面内自由振动振型;ω为非圆弧陡拱结构自由振动振型v(z)对应的振动频率。将式(16)代入式(11),可得式(11)的不平衡差为

(17)

将式(13)对变量z积分两次,可得

(18)

将式(18)代入式(17)并对变量z积分两次,可得

(19)

由于非圆弧拱弧长曲线微分项1+y′2的存在,式(19)不能恒等于零。若退而求其次,令不平衡差在全拱范围内对变量z积分为零

(20)

可求得非圆弧陡拱自振频率ω的实用解析。将式(19)代入式(20),可得

ω≈ξω0

(21)

式中,ξ为非圆弧陡拱自振频率系数。

(22)

当拱轴线为悬索线时

(23)

将式(23)代入式(22),可得悬索线陡拱自振频率系数为

(24)

当拱轴线为抛物线、悬链线、组合线[16-17]等其他非圆弧拱轴时,可采用近似曲线积分方法[18]得到如式(24)所示的其他非圆弧陡拱自振频率系数ξ,具体数值如表1所示。

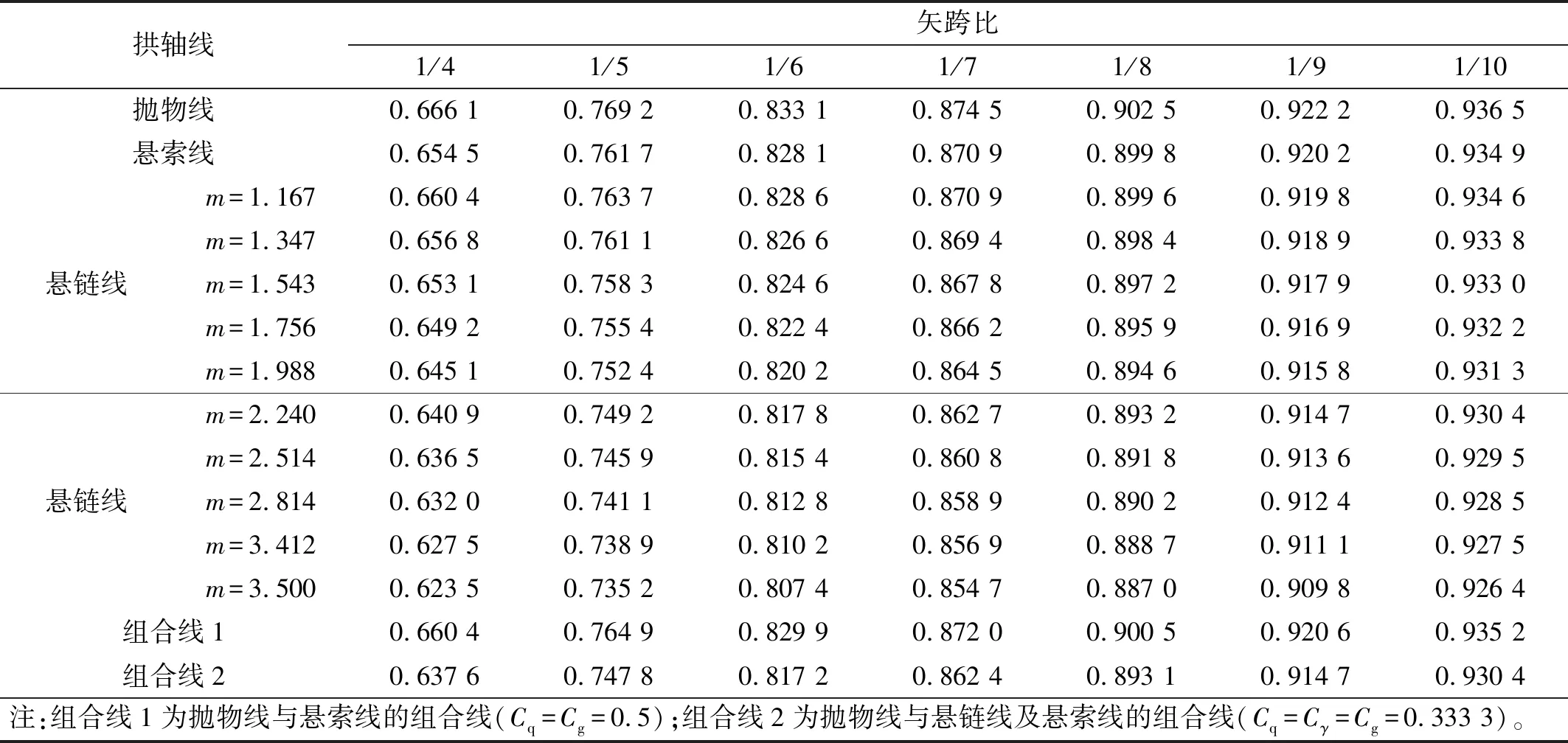
表1 非圆弧拱自振频率系数ξ

将两铰拱边界条件

(25)

代入式(15)可得非圆弧两铰拱振型函数为

(26)

式中:c5为任意常数;n为正整数,n=2,3,…。将如式(25)所示两铰拱边界代入式(13)与式(21),可得非圆弧两铰陡拱自振频率实用解析为

(27)

将无铰拱边界条件

(28)

代入式(15)可得非圆弧无铰拱振型函数为

(29)

式中:c6为任意常数;γ为系数,可表示为

(30)

式中,θk为常数,可表示为

(31)

式中:k为整数,k=1,2,…。将如式(28)所示无铰拱边界代入式(13)与式(21),可得非圆弧无铰陡拱自振频率实用解析为

(32)

由式(13)可以看出,非圆弧浅拱面内自由振动平衡微分方程与同参数直梁相同,进而导致两者自振频率也相同。由式(21)、式(27)与式(32)可知,非圆弧陡拱面内自振频率在数值上与同参数非圆弧浅拱自振频率之间,存在1个恒定参数ξ的比例关系,而该系数仅与矢跨比有关。该规律的发现,在理论上首次揭示了非圆弧拱结构与同参数直梁面内自振频率的关系,可为行业规范条文修订提供参考。

3 算例验证

为验证本文提出的基本假定与非圆弧拱结构面内线性自由振动频率高精度实用解析,选择跨径L=100 m、矢跨比为f/L=1/10～1/4的非圆弧拱结构作为算例。拱轴线选取抛物线、悬索线、拱轴系数3.500的悬链线、抛物线与悬索线组合线(Cq=Cg=0.5)、抛物线与悬链线及悬索线的组合线(Cq=Cγ=Cg=0.333 3);主拱圈横截面为半径1 m的圆形,面积A=3.141 59 m2,惯性矩Ix=0.785 4 m4;材料弹性模量E=210 GPa,泊松比v=0.2。

使用有限元软件ANSYS作为本文算例数值计算平台。在以上结构参数基础上,使用两节点6自由度空间梁单元Beam4建立本文算例自由振动有限元模型。在两拱脚处节点设置平面内铰接或固接边界,并在所有节点设置面外线位移约束以防止发生面外振动。使用结构模块计算本算例非圆弧两铰拱和无铰拱前十阶自振频率,并通过后处理模块导出本算例非圆弧两铰拱和无铰拱前十阶振型与自振频率数据。收敛验证结果表明,含有300个BEAM4梁单元且水平方向均匀划分单元节点的有限元模型,可较好地兼顾有限元规模与自振频率精确性。提取非圆弧两铰拱和无铰拱自由振动数值结果,用以验证本文基本假定与实用解析公式。

3.1 基本假定验证

陡拱与浅拱振型没有显著差异基本假定,是本文方法中非圆弧拱变系数平衡微分方程近似解析的基础,必须得到严格的检验。

为验证陡拱与浅拱振型没有显著差异基本假定不随矢跨比的变化而变化,提取算例中矢跨比f/L=1/10～1/4抛物线两铰拱与无铰拱结构一阶振型的正交规范化模态,与本文方法振型函数式(26)和式(29)进行比较。本文方法振型函数与有限元法结果的比较,如图2所示。由图2可知,矢跨比f/L=1/10～1/4两铰拱与无铰拱的一阶振型函数,均与本文方法式(26)和式(29)吻合较好,表明陡拱与浅拱振型没有显著差异基本假定适用于不同矢跨比非圆弧拱结构。

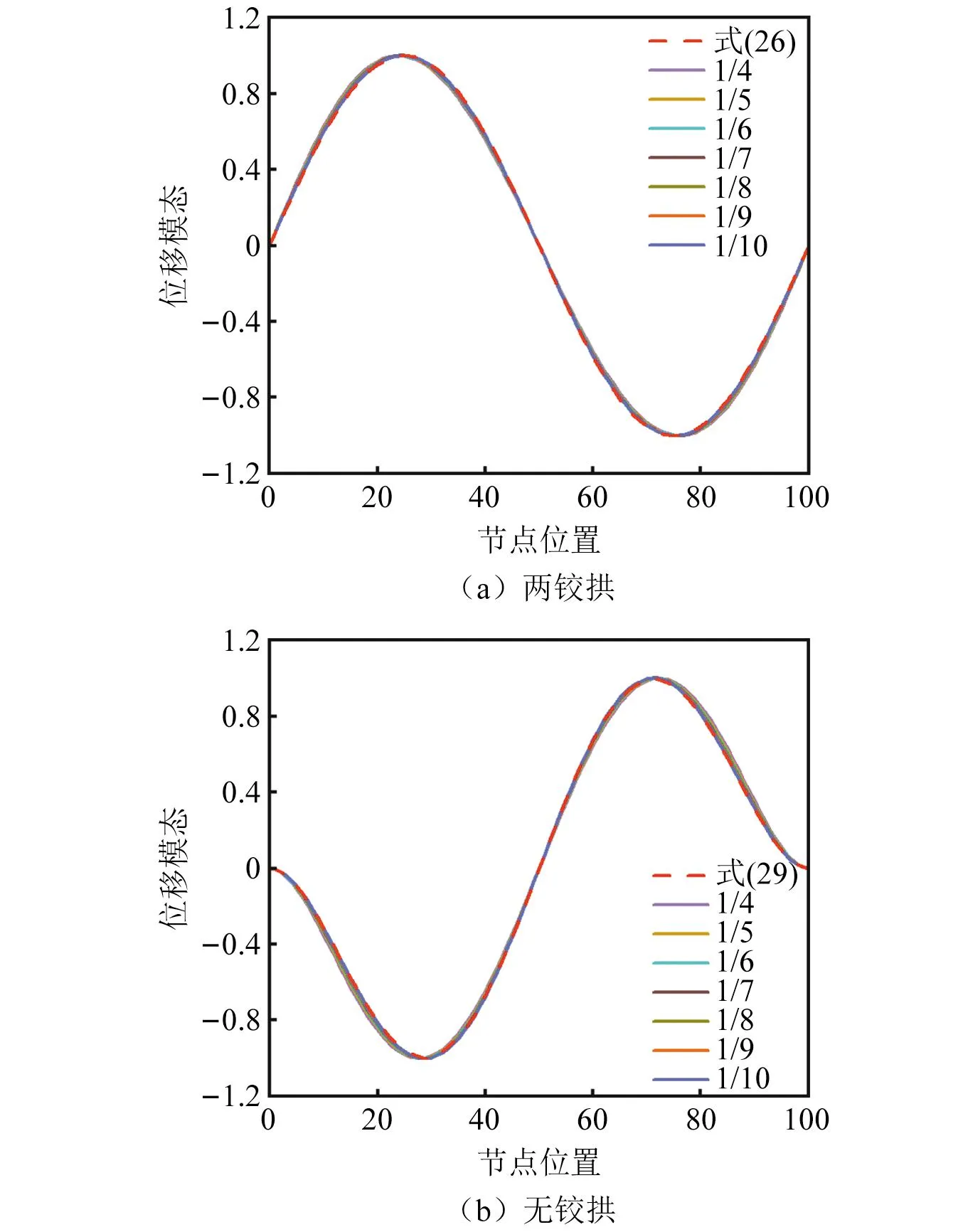
图2 不同矢跨比振型函数验证

为检验陡拱与浅拱振型没有显著差异基本假定不随振型阶次的变化而变化,选取矢跨比1/5的悬索线两铰拱与无铰拱,提取有限元解中第一阶至第五阶结构振型的正交规范化模态,分别与本文方法式(26)和式(29)进行对比,如图3所示。由图3可知,矢跨比1/5的悬索线两铰拱与无铰拱前五阶结构振型,均与本文方法式(26)和式(29)吻合较好,表明陡拱与浅拱振型没有显著差异基本假定适用于非圆弧拱结构不同阶次振型。

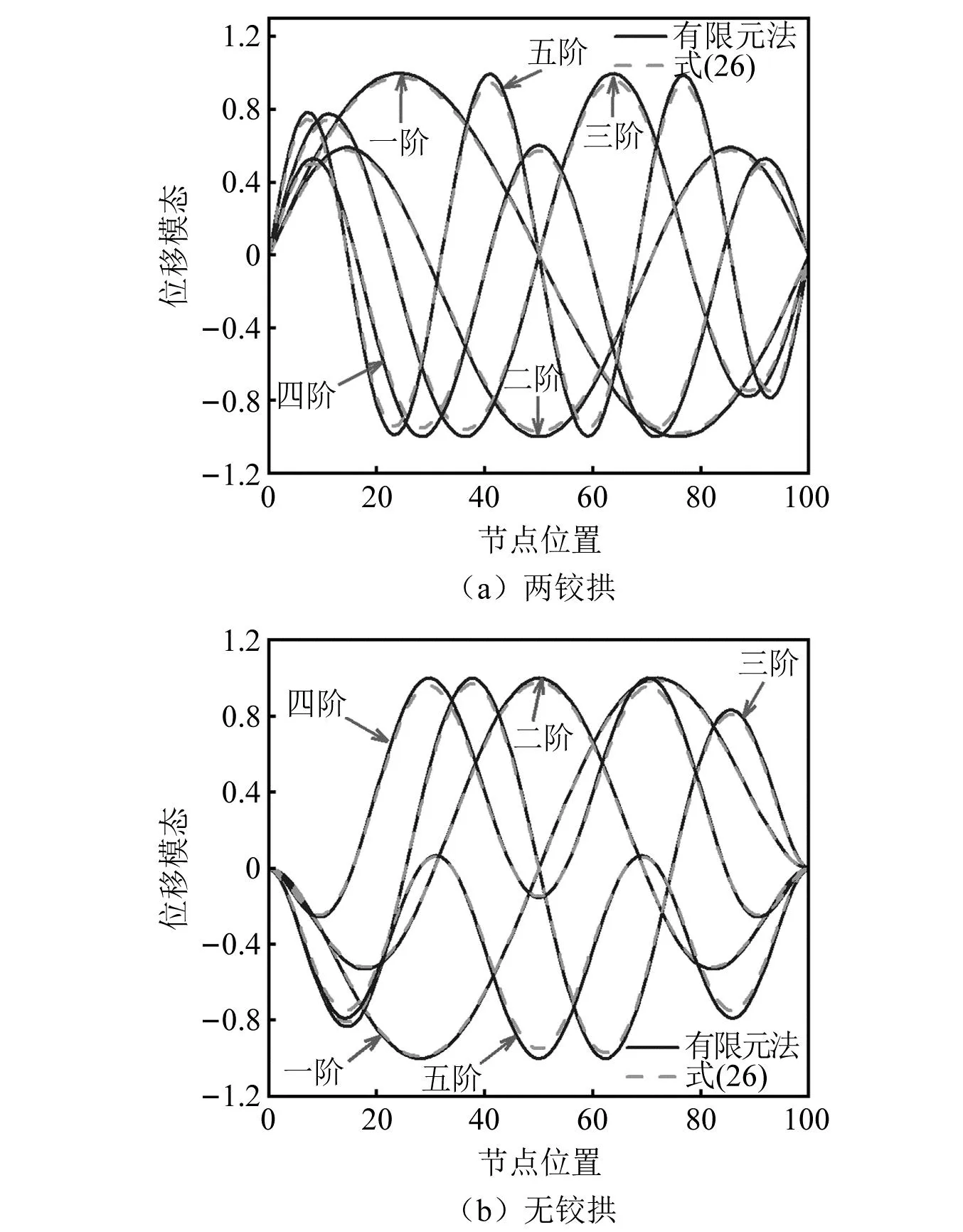
图3 不同阶次振型函数验证

为检验陡拱与浅拱振型没有显著差异基本假定不随拱轴线的变化而变化,选取抛物线、悬索线、拱轴系数3.500的悬链线、抛物线与悬索线(Cq=Cg=0.5)组合线、抛物线与悬链线及悬索线的组合线(Cq=Cγ=Cg=0.333 3),提取矢跨比1/8两铰拱与无铰拱有限元解中第五阶振型的正交规范化模态,分别与本文方法式(26)和式(29)进行对比,如图4所示。由图4可知,在五种不同的非圆弧拱轴线中,本文方法式(26)和式(29)均与有限元解吻合较好,表明陡拱与浅拱振型没有显著差异基本假定适用于不同非圆弧拱结构。

图4 不同拱轴线第五阶振型函数验证

非圆弧拱结构以竖向振动为主,水平振幅远比竖向振幅小基本假定,是本文非圆弧拱变系数平衡微分方程建立的基础,也必须得到严格的检验。

为检验非圆弧拱以竖向振动为主基本假定不随矢跨比的变化而变化,提取算例中矢跨比抛物线两铰拱与无铰拱结构一阶振型的竖向与水平分量,两者对比结果如图5所示。由图5可知,不同矢跨比下抛物线两铰拱与无铰拱结构一阶振型的竖向振幅均大于水平振幅,且水平振幅始终在较小的范围内,表明以竖向振动为主基本假定适用于不同矢跨比非圆弧拱结构。

图5 不同矢跨比振幅验证

为检验非圆弧拱以竖向振动为主基本假定不随振型阶次的变化而变化,提取算例中矢跨比1/5悬索线两铰拱与无铰拱有限元解中第一至第三阶振型的竖向与水平振幅分量,两者结果对比如图6所示。由图6可知,悬索线两铰拱与无铰拱第一至第三阶振型的竖向分量始终大于水平分量,表明非圆弧拱以竖向振动为主基本假定适用于非圆弧拱结构不同阶次振型。

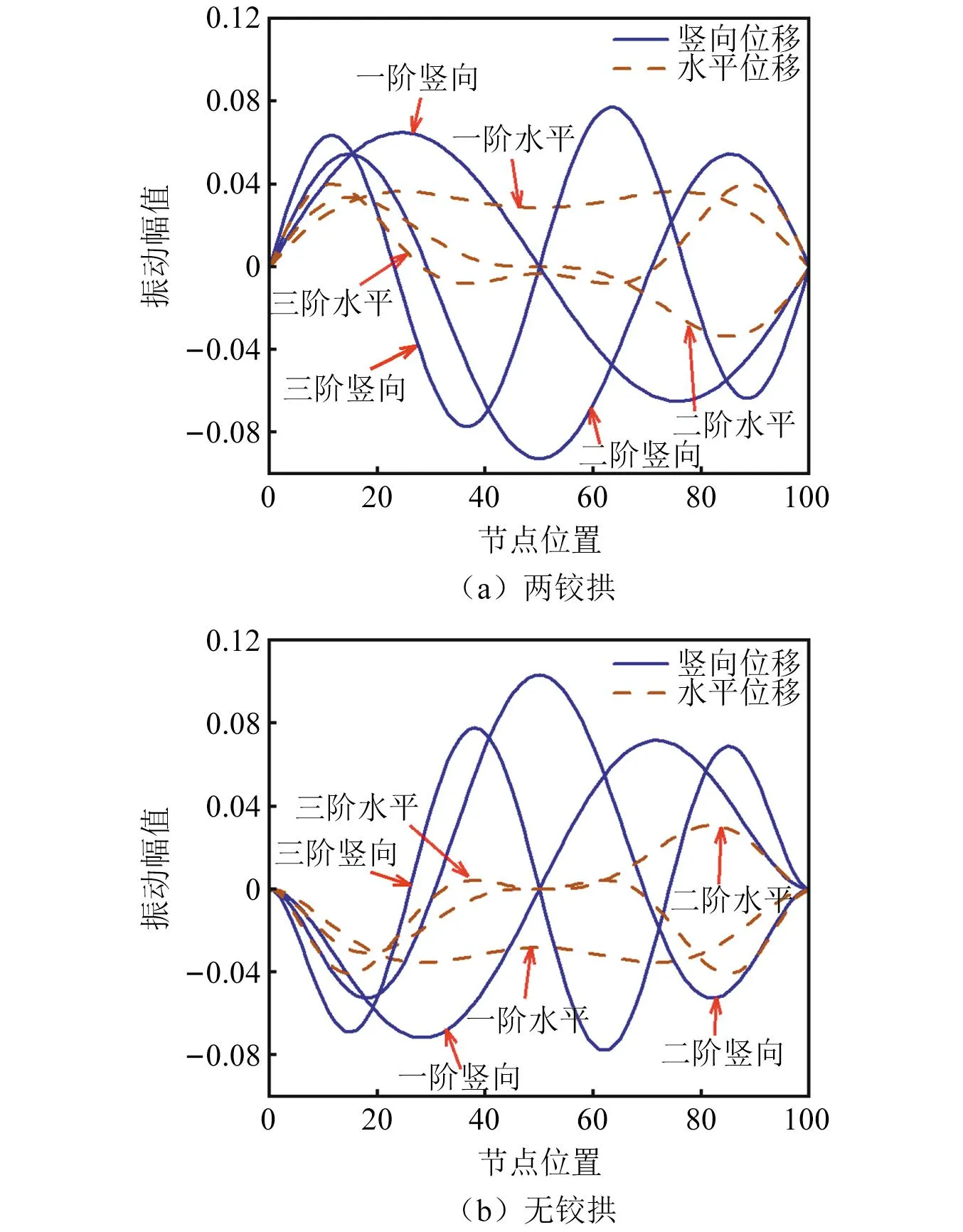
图6 不同振型振幅验证

为检验非圆弧拱以竖向振动为主基本假定不随拱轴线的变化而变化,选取抛物线、悬索线、拱轴系数3.500的悬链线、抛物线与悬索线(Cq=Cg=0.5)组合线、抛物线与悬链线及悬索线的组合线(Cq=Cγ=Cg=0.333 3),提取矢跨比1/8两铰拱与无铰拱有限元解中第五阶振型中的竖向与水平分量,两者对比结果如图7所示。由图7可知,不同非圆弧拱竖向振幅远大于水平振幅,且水平振幅始终在较小的范围内,表明以竖向振动为主基本假定适用于不同拱轴线的非圆弧拱结构。

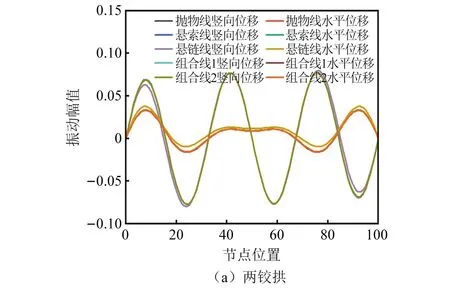
图7 不同矢跨比振幅验证

3.2 自振频率验证

为检验本文方法非圆弧拱面内自由振动实用解析的精确性,提取有限元算例中矢跨比f/L=1/10～1/4抛物线两铰拱与无铰拱结构前十阶频率数值结果,与本文方法自振频率实用解析式(27)和式(32)进行比较,本文方法所得自振频率数值如图8所示,两者的相对误差如图9所示。由图9可知,与有限元结果相比本文方法具有较好的精度,无铰拱相对误差小于两铰拱;无铰拱最大相对误差小于5%,两铰拱最大相对误差为7.71%,为矢跨比为1/5抛物线两铰拱第六阶自振频率,具体数值如表2所示。

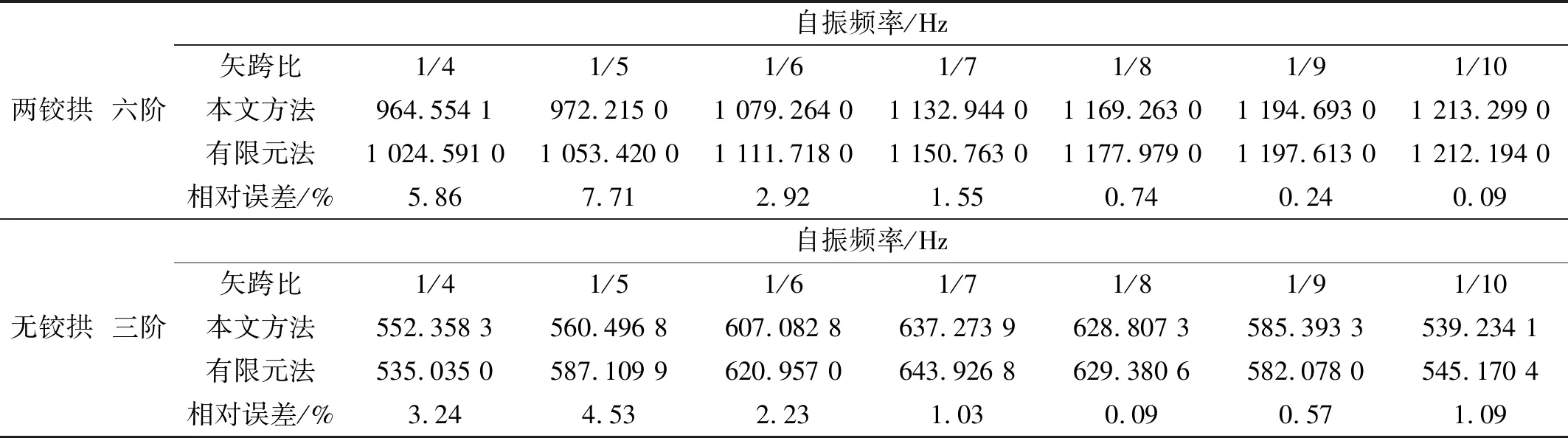
表2 不同矢跨比下抛物线自振频率最大误差验证

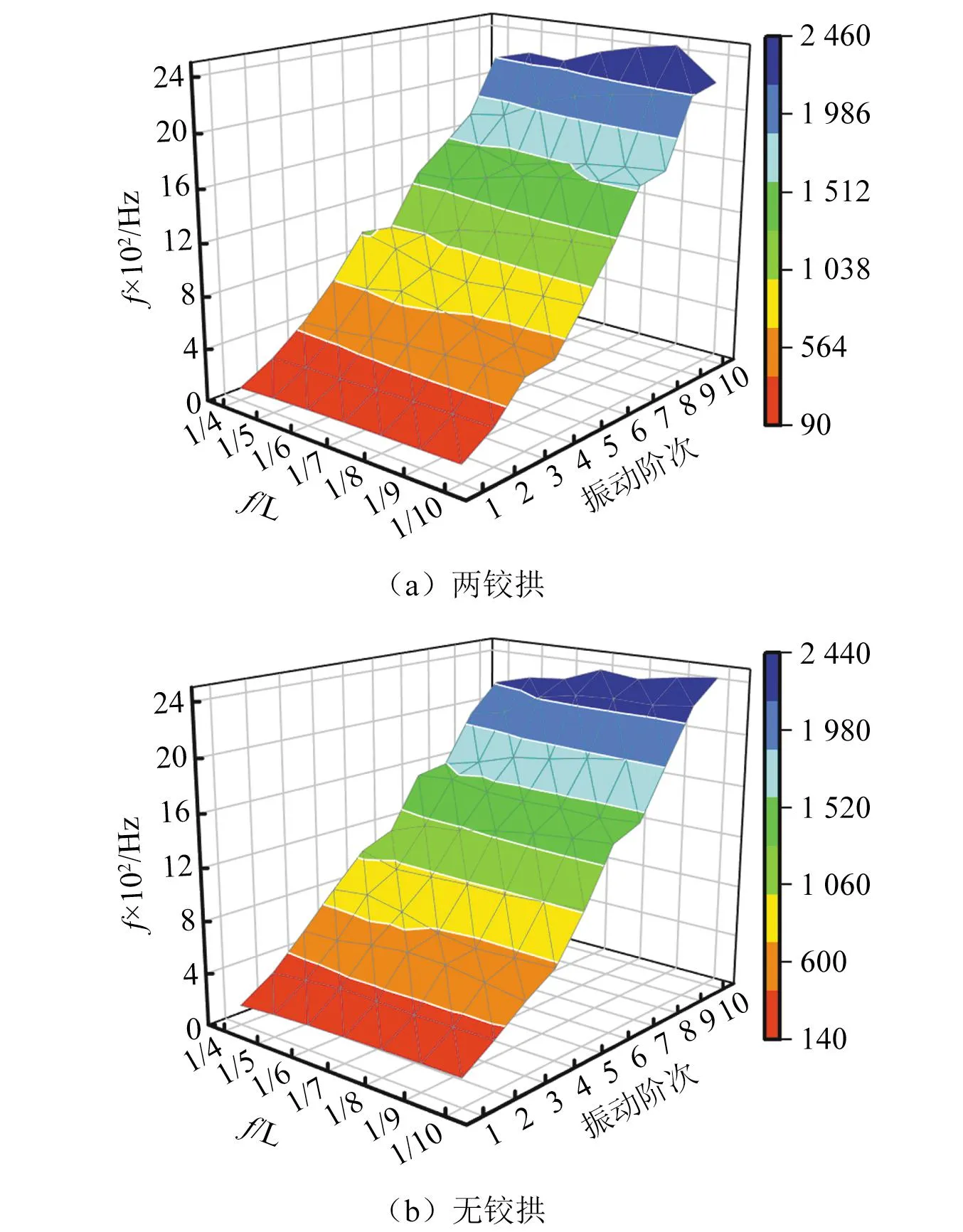
图8 本文方法抛物线拱自由振动频率

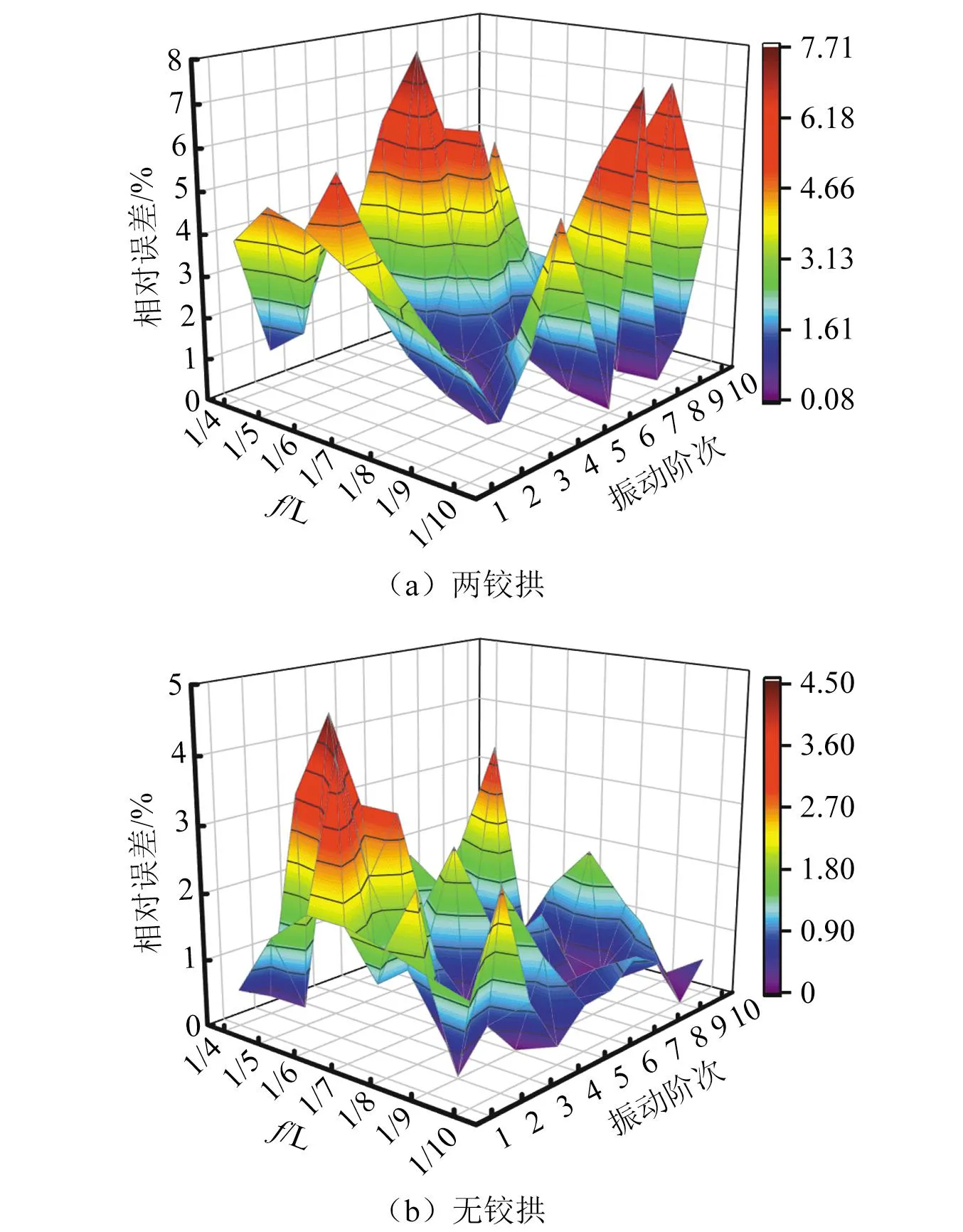
图9 抛物线拱自由振动频率验证

为检验本文方法非圆弧拱面内自由振动实用解析在各种非圆弧拱轴线下的精确性,提取有限元算例中矢跨比f/L=1/10～1/4、拱轴系数m=1.167～3.500悬链线两铰拱与无铰拱结构第六阶自振频率数值结果,与本文方法式(27)和式(32)进行对比,本文方法所得非圆弧拱第六阶自由振动频率数值如图10所示,两者的相对误差如图11所示。由图11可知,与有限元结果相比本文方法具有较好的精度,无铰拱相对误差小于两铰拱;无铰拱最大相对误差小于5%,两铰拱最大相对误差为7.48%,为矢跨比为1/5拱轴系数m=3.412悬链线两铰拱结构,具体数值如表3所示。

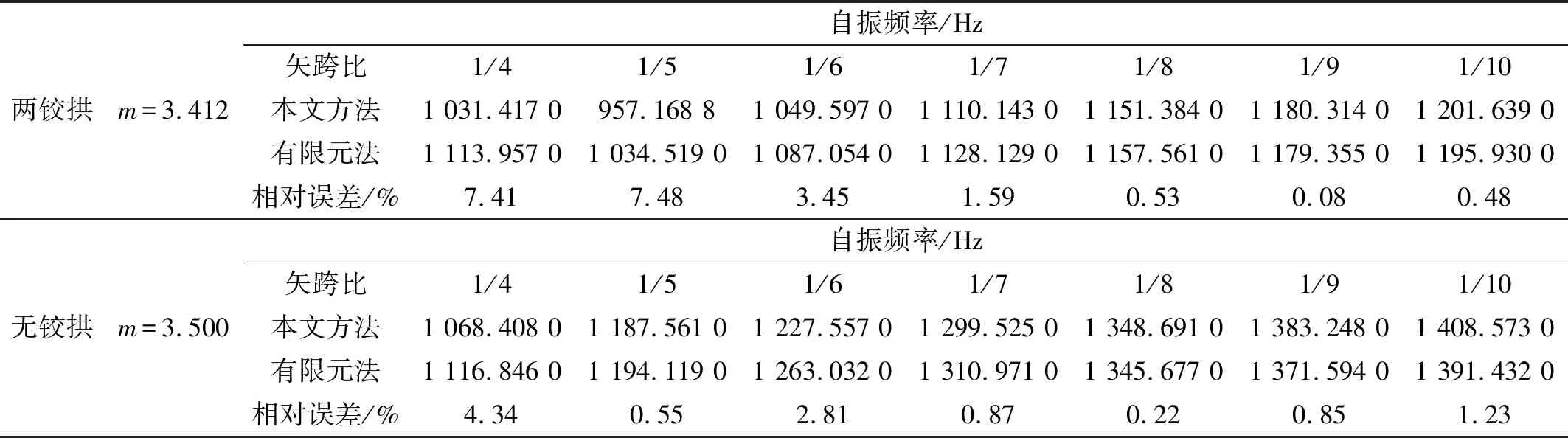
表3 不同拱轴系数悬链线自振频率最大误差验证

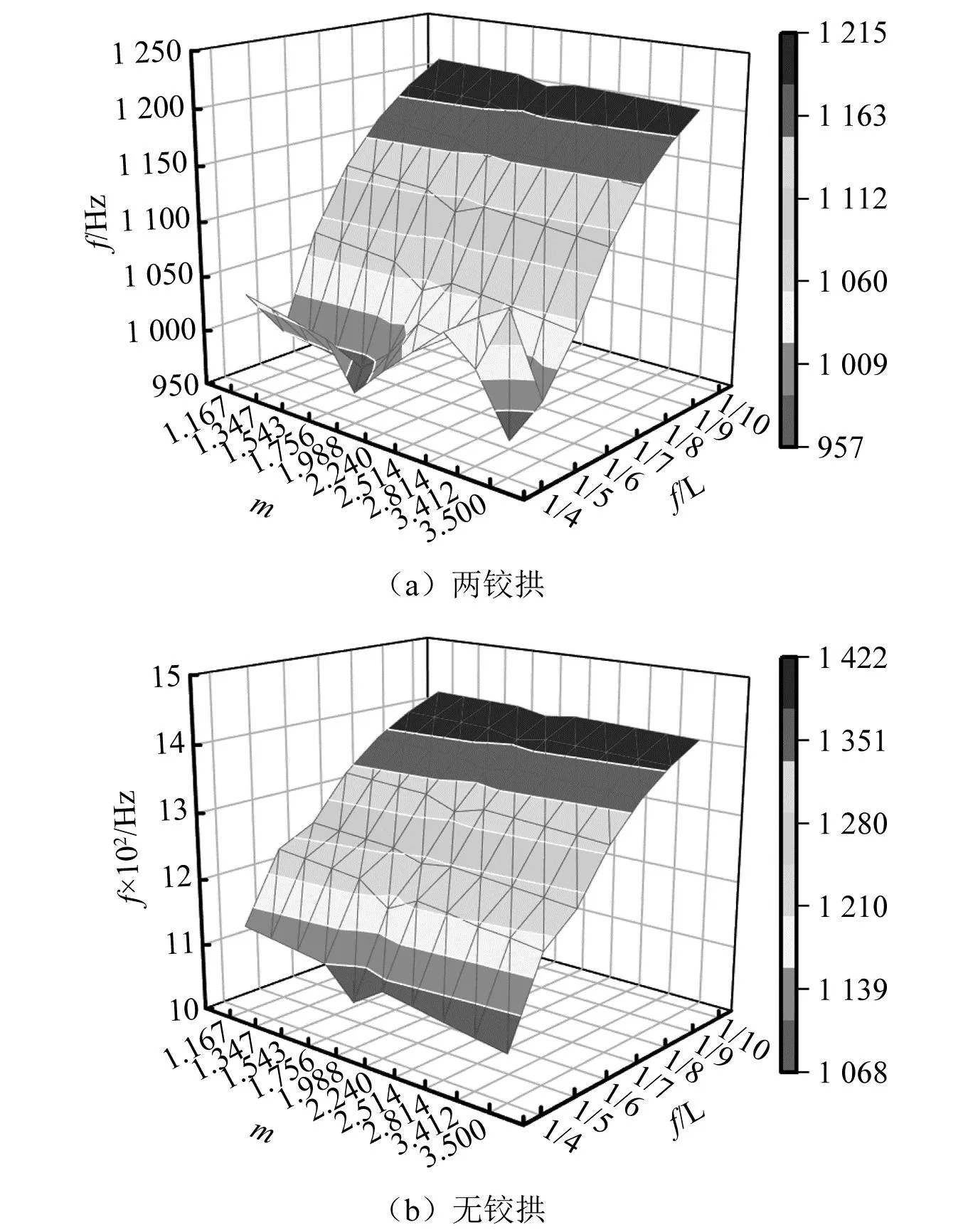
图10 本文方法非圆弧拱第六阶自由振动频率

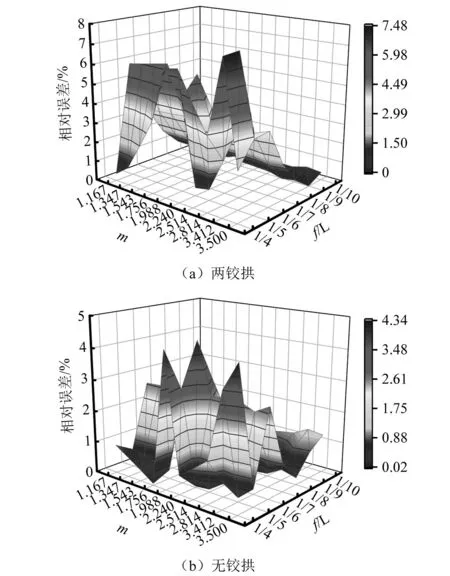
图11 非圆弧拱自由振动频率验证

综合图8、图9、图10与图11,可以得出本文方法非圆弧拱面内自由振动实用解析满足工程精度要求的结论。

4 结 论

本文针对直角坐标系下非圆弧拱面内自由振动没有解析的现状,提出了一种变系数平衡微分方程的解析方法。基于笛卡尔直角坐标系下拱结构线性应变表达式与Hamilton原理,推演了抛物线拱面内自由振动变系数平衡微分方程;将该变系数平衡微分方程对应常系数平衡微分方程的通解,代入变系数平衡微分方程得到不平衡差,当该不平衡差沿全拱的积分为零时,得到抛物线拱面内自振频率高精度实用解析;并通过有限元解验证了本文方法,基于此,得到以下结论:

(1) 本文提出的变系数平衡微分方程近似解析方法,可以推演得到直角坐标系下非圆弧拱结构面内自由振动的高精度实用解析。

(2) 拱桥工程中常用非圆弧拱陡拱与浅拱振型没有显著差异。

(3) 非圆弧面内自由振动频率,与同参数直梁非一阶自振频率,存在恒定参数比例关系。

(4) 本文推演的拱结构自由振动频率的高精度近似解析,与有限元结果吻合较好,满足工程应用精度要求。