基于EMD-RF模型的唐山市径流量预测研究
2024-03-01陈研研
陈研研
(河北省唐山水文勘测研究中心,河北 唐山 063000)
0 引言
随着全球气候变化日益严重,水资源合理利用和预测成为一个亟待解决的问题。唐山作为我国北方工业重城,其径流量变化对城市经济发展和人民生活有重要影响,因此,对唐山径流量进行准确预测具有实践意义[1-3]。过去研究中许多学者采用单一机器学习模型如线性、支持向量机(SVM)、反向传播(BP)、极限学习机(ELM)和神经网络等方法进行预测[2-6]。然而,该方法往往忽视了径流量序列内在隐含的信息,导致预测准确性不高。为解决这一问题,本文提出一种基于集合经验模态分解(EMD)和随机森林(RF)耦合的模型[7-8]。EMD是一种能提取非线性和非平稳信号内在模式的分解法,可将复杂径流量序列分解为一系列的固有模态函数(IMFs)。这些IMFs包含径流量序列主要信息,可以用于后续预测模型。而RF是一种强大的机器学习算法,其通过构建多个决策树并结合它们的结果来进行预测[8],进而可提升模型拟合能力。本文以唐山为例证,以验证EMD-RF策略的有效性。
1 研究区与方法
1.1 研究区与数据来源
唐山位于河北东北、渤海湾北岸、燕山南侧,地理坐标为117°31′~119°19′E、38°55′~40°28′N,总面积13 472 km2。地势自北向南倾斜,海拔介于0~842 m(见图1),形成土石山、平原地形,东南为滨海低地,海岸线长229.7 km。属典型暖温带半湿润大陆型季风性气候,具有四季分明、炎夏寒冬、雨热同期特点,多年平均气温9.6℃,降水量690 mm。主要河流为滦河,河川径流量14.62亿m3,但人均占有量不足全国平均水平的1/10。本研究使用的径流量资料来自唐山水文局滦河的主要径流量数据。其时间范围为1960年1月至2020年12月,共计时间尺度60年(720个月)。为确保模型公正性,选取1960-2000年(40年,480个月)的径流量资料作为训练集,以2001-2020年(20年,240个月)数据为验证集。在运用EMD-RF方法执行训练前,需对原数据进行归一化处理以减小数据噪声,归一化方式如下:

图1 研究区地形和主要河流分布
y=log10(x)
式中,x、y分别为归一化之前、后的径流量[5-7]。
1.2 随机森林算法
随机森林(RF)回归算法是一种集成学习算法,其基本单元是回归分类树(Classification and Regression Tree,CART)。在建模过程中,RF会构建多个CART,并且每棵CART都是在随机选择的子样本上独立进行训练的,这样可以有效地降低过拟合的风险。对于新的输入样本,RF通过将多棵决策树的预测结果进行平均或加权平均,从而得到最终的回归结果。从数学的角度来看,RF的目标是最小化所有CART的残差平方和之和。具体而言,有n个样本和m个特征,则目标函数可以表示为:
式中,yi是第i个样本的目标值;xij是第i个样本的第j个特征的值;fj(xij)是第j个特征在第i个样本上的预测值。这个目标函数实际上是在寻找一个函数族,使得所有样本上的预测值与真实值之间的差距(即残差)的平方和最小[6-8]。
1.3 经验模态分解算法
经验模态分解(EMD)算法能够自适应地分解任意复杂信号为多组分成分[2-5]。其原理是将一个信号投影到时频平面上,使每次投影成为一个模式分量,对原始信号通过频率阶数由高至低进行分离得到多个模式分量,并保持每个模式分量的时变特性,从而能够通过频谱变换计算相应的瞬时频率。其过程如下:
(1)找到原始信号X(t)的极大值和极小值点,然后通过曲线插值方法对这些极值点进行拟合,得到信号的上包络线Xmax(t)和下包络线Xmin(t)。
(2)对上下包络线求平均值:
(3)对原始信号X(t)与平均包络m1(t)进行相减,得到余下信号d1(t)。
(4)一般情况下,对于平稳信号而言,它是原始信号X(t)的第一个模态函数(IMF)。但对于非平稳信号,信号并不是在某一个区域内单调递增的,而是会出现拐点。这些能反映原始信号X(t)的具体特征的拐点若未被选中,则得到的第一阶模态函数并不准确,也就是通常得到的d1(t)并不是一个IMF,因此需要对d1(t)进行再一次的EMD分解[6-8]。
2 结果与分析
2.1 径流量时间序列特征
如图2所示,研究区逐月径流量变化极具跃迁性,观测到径流量最高值为172.36 m3/s,另外还存在164.6、151.5、138.6 m3/s的极高值,极小值仅5.03 m3/s,统计平均值18.94 m3/s,变差系数64.36%,表明月际径流量变异性强烈。不难分析径流量序列年内存在丰枯交替变化,这与本地雨热同季的气候特征一致。经线性回归分析表明,其变化趋势为y= -0.012 8x+23.397,R2=0.012 6,但并未通过5%水平置信度检验,但依然可发现自近200个月以来的径流量时变性减弱、极大值减小,表明近年来气候变化与人类活动影响下区域径流量逐渐萎缩,也显示出径流量变化的复杂性。

图2 唐山市地表径流量逐月序列变化
2.2 径流量EMD特征
利用EMD方法对研究区径流量进行模态分解,得到7个IMF分量和一个残差项,其结果见图3。该图直观呈现了径流量变化幅值、频率和时间尺度等特征,帮助了解信号的局部特征和变化趋势。其中,IMF1-IMF2为高频分量,其反映了径流量的逐月、季节性变化周期,计算得到样本熵依次为9.87、7.63;IMF3、IMF4为中频分量,代表了径流量年际震荡特性,相应的样本熵为4.32、2.17;IMF5、IMF6、IMF7分别为低频分量,其承载的信号较低,样本熵依次为1.63、0.45、0.12。该不同频率的IMF特征与残差项的加和可直观重构径流量变化特征,因此,IMF分量是径流量的多尺度解析特征。
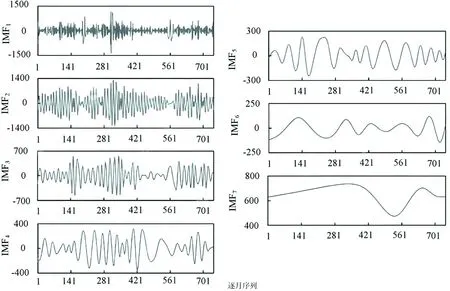
图3 唐山市地表径流量EMD特征
2.3 EMD-RF模型建立
首先运用EMD方法将原径流量序列分解为若干模态函数(IMF)和一些趋势项残差(RSE),随后以此作为解释变量,分别使用t-1月的数据预测t个月的径流量,RF可拟合任意非线性的函数曲面。通过Rstudio开源程序语言Caret工具,设计RF回归模型,输入数据为数值型特征。在RF模型中mtry表示为单一回归树中输入变量数,而ntree为树总数,全部回归树预测结果构成一片森林,通常mtry和ntree综合影响RF模型精度。如图4所示,选定较小的mtry范围,ntree搜索区间为100~1 000,最终确定当mtry=3、ntree=500时,模型训练精度决定系数R2达到最高值,为0.96,由此确定模型结构配置。

图4 RF模型精度随参数变化趋势
2.4 基于EDM-RF模型的径流量模拟及其精度评价
将全部7个IMF分量作为
输入变量,将训练好的模型带入数据集,仿真生成径流量变化序列,其结果见图5。图中模型预测值与实际值之间具有良好一致性,呈现相似涨跌过程,并准确捕获了极大、极小过程值。利用纳西效率(NSE)、均方根误差(RMSE)对验证集进行评估,得到NSE为0.93,RMSE仅为7.12 m3/s,显然该NSE接近于1、RMSE较小,表明该模型预测精度在可接受范围内,该径流量仿真预测结果可信度高。需要指出的是,仍然存在一定误差,对此尚需进一步优化改进。
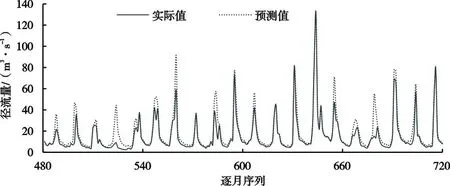
图5 基于EMD-RF模型的径流量预测精度
3 结论
本研究将EMD与RF回归算法相耦合,新建基于EMD-RF的月径流量预测模型,对唐山市近60 a来径流量进行预报研究,结论如下:
(1)唐山月径流量被划分为7个IMF分量,其中IMF1、IMF2为高频分量,IMF3、IMF4为中频分量,IMF5、IMF6、IMF7为低频分量;
(2)在月径流量预报时,RF模型表现出良好拟合性能,但需要优化配置模型mtry、ntree参数;
(3)验证表明EMD-RF模型精度高、误差较低,该方法有望为月径流预测提供新策略。
