水闸非线性水动力学建模与数值模拟方法研究

姜 燕,吴美玲,金敏娇

(宁波弘泰水利信息科技有限公司,浙江 宁波 315000 )

0 引言

水闸非线性水动力学建模与数值模拟方法研究在实际工程和水资源管理中具有重要的意义[1-2]。许多水利工程中涉及水闸的设计和运行,而水闸门的开启与关闭过程往往涉及复杂的水动力学现象,室内试验很难捕捉其动力学特征,尤其是在涉及高宽比流动的情况下。因此,探讨水闸非线性水动力学行为,并开发相应的数值模拟方法,可以更好地理解和预测水闸开启和关闭时的水动力情况[3-4]。然而,当前国内学者大多通过常规的连续性数值方法对水闸的水动力特性进行研究。付志坤等[5]借助ANSYS Workbench分析系统,以数理模拟计算分析的方式,对泄水闸室静冰温度梯度进行多参量数理模拟计算分析,探究泄水闸室冰层的静冰压力分布状态和规律;代彬等[6]为提高闸门流量建模精度,引入先进的可实现k-epsilon模型,对某沉水闸下游流场进行建模;何平[7]以某水闸为例,采用ABAQUS有限元软件,对桩基础水闸在不同工况下的渗流进行了数值模拟;张延等[8]基于某斜水闸侧壁工程实例,在对水闸侧壁倾斜工况模拟方案进行对比分析的基础上,结合相关有限元分析软件进行数值模拟分析,逐步实施一套斜流导向卸荷反压导向方案。以上结果大多是通过连续性方程计算而得到。然而,在许多实际情况中,水闸门的开启和关闭会引发水流的非线性响应,这可能包括液体跃变、湍流涡旋、湍流耗散等复杂现象,常规方法无法捕捉这一动力学特征。本研究通过使用当前最流行的平滑粒子流体动力学(Smoothed Particle Hydrodynamics,SPH)方法,旨在建立水闸非线性水动力学的数学模型,并优化数值模拟方法,以更准确地捕捉这些复杂的水动力学现象[9]。

1 SPH 方法

平滑粒子流体动力学(SPH)方法是一种离散的无网格方法,其中,将流体体积划分为有限数量的粒子,通常是均匀大小和性质的粒子。与其他拉格朗日方法一样,由于粒子不固定在空间中,它们的运动是通过质量守恒和动量守恒的流体动力学方程来模拟的[10]。当然,还必须考虑到模拟流体物理状态所需的任何适用方程(例如,密度、粘度、温度的变化)。SPH方法与牛顿粒子方法(如多粒子方法(MPM)和粒子在网格单元中的方法(PIC)相比的主要区别在于：任何单个粒子都与其直接相邻的邻居及空间半径等于h的那些粒子相互作用。如图1所示。为了避免粒子的不自然的扭曲行为,与邻近粒子距离越远,它对其邻居的影响就越小。在SPH方法中,通过称为核函数W(x,h)的加权函数来实现这一点,该函数可以是任何连续的、空间对称的函数。

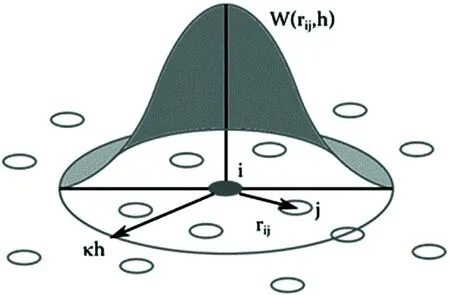
图1 SPH 方法示意

2 水闸模型

本文研究了一个长型(50∶1)、水平的开放式流动通道,如图2所示。所有模拟均采用了均匀大小的二维粒子,并将它们排列成均匀间隔的矩形阵列,使用莫里斯动量守恒方程来演化动量,以及蒙加汉状态方程和人工声速c0= 80 m/s,因为流体速度预计远低于10 m/s。另外,还赋予粒子T= 20°C下的纯净水的物理性质(粘度=0.000 896 Pa·s,密度=998 kg/m3),并都使用具有平滑函数W(x,h)的立方形式,其中,平滑长度为h等于1.1倍的粒子大小,这是解约计算成本的一个典型值。对于边界条件,所有固体边界包括静态闸门均由一行均匀间隔的虚拟粒子建模的,其力学行为通过蒙加汉排斥力方程建模,该方程只在距离边界粒子一定范围r0内的流体粒子附近产生影响,并且与边界粒子和流体粒子之间的距离成反比关系(这个比例关系可以根据用户经验调整)[11]。本次计算时间为t=5.0 s,含20 000个颗粒。

图2 数值模型

3 数值结果分析

图3到图5是关于不同计算时间下数值模拟结果的图示。图3给出了计算时间小于1.2 s时的情况。在这个时间点,可以看到开放的排水区域(即开放的闸门)和靠近边界的颗粒。此时,流体颗粒的排列呈现出相对规则的状态。这可能是因为在初始时刻,流体颗粒的初始分布是均匀的,没有明显的液体积聚或不规则分布。然后,随着时间的推移,特别是在图4和图5所示的时间点,可以看到颗粒的分布变得更加不规则[12]。这种不规则性主要集中在靠近闸门的区域,这是由于靠近闸门区域的复杂流体动力学作用所致。流体开始在排水区域积聚,导致该位置的水位下降。这一现象在图4和图5中非常明显,显示了在这个时间段内流体颗粒的分布发生了显著变化。但是,尽管流体颗粒的分布变得更加不规则,仍然可以观察到一些定量的特征[13]。例如,在图4和图5中,可以看到排水喷射的初始深度,当孔径为0.2 m时,位于x= 50 m的位置,大致为0.12 m(解析解给出的深度为0.13 m)。随后,这个喷射在短距离内扩展到约0.16 m深。这种扩展的过程与流体的动力学有关,而且与传统的水流在干燥床上流动的方式相似。另一方面,这些数值模拟结果与解析解非常接近,表明了模型的准确性和可靠性,如图6所示。

图3 在 t = 0.5 s时水闸门水力剖面细节

图4 在 t = 2.5 s时水闸门水力剖面细节

图5 在 t = 5 s时水闸门水力剖面细节

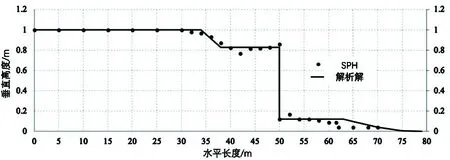
图6 在 t = 5 s时水闸门水力解析解与数值解对比

4 结论

本研究采用了平滑粒子流体动力学(SPH)方法,通过将流体划分为有限数量的粒子来模拟流体的运动。数值结果分析表明,SPH方法可以有效地模拟水闸开启和关闭过程中的水动力学现象,包括流体颗粒的不规则分布和排水喷射的变化。与解析解相比,这些数值模拟结果非常接近,证明了模型的准确性和可靠性。因此,采用SPH方法进行水闸非线性水动力学建模与数值模拟是一种有效的方法,可以帮助工程师和水资源管理者更好地理解和预测水闸的水动力情况,从而提高水闸设计和运行的效率和安全性。